山东省高密市高密四中文慧学校2016届九年级下学期第一次月考数学试题
文档属性
| 名称 | 山东省高密市高密四中文慧学校2016届九年级下学期第一次月考数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-08 00:00:00 | ||
图片预览



文档简介
山东省高密市高密四中文慧学校2015-2016学年下学期九年级数学第一次月考(4月)
一.选择题(每小题3分,共36分)
1.(2016 南岗区一模)下列计算正确的是( )
A.2a+3a=6a B.a2 a3=a6 C.a8÷a4=a2 D.(﹣2a3)2=4a6
2.(2015 随州)若代数式+有意义,则实数x的取值范围是( )
A.x≠1 B.x≥0 C.x≠0 D.x≥0且x≠1
3.(2016 安徽模拟)2015年春运期间,全国有23.2亿人次进行
东西南北大流动,用科学记数法表示23.2亿是( )
A.23.2×108 B.2.32×109 C.232×107 D.2.32×108
4.(2015 攀枝花)如图所示的几何体为圆台,其俯视图正确的是( )
A. B. C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.(2015 庆阳)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. ( http: / / www.21cnjy.com ) D.
6.(2016 锦江区模拟)已知关于x的一元二次方程x2﹣2x﹣3=0
两实数根为x1、x2,则x1+x2的值是( )
A.3 B.﹣3 C.2 D.﹣2
7.(2016 安徽模拟)如图,等腰△ABC中,AB=AC=8,BC=5,
AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的
周长为( )
A.13 B.14 C.15 D.16
8.(2015 长沙县模拟)若2a﹣b=3,则9﹣4a+2b的值为( )
A.3 B.6 C.12 D.0
9.(2015 包头一模)若点P(2k﹣1,1﹣k)在第四象限,则k的取值范围为( )
A.k>1 B.k< C.k> D.<k<1
10.(2015 黔东南州)若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
11.(2015 乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
A. B. C. D.
12.(2016 深圳模拟)如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( )
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
A.1 B.2 C.3 D.4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(第11题) (第12题)
二.填空题(每小题3分,共18分)
13.(2015 德州)方程﹣=1的解是 .
14.(2015 昆山市一模)因式分解:x3﹣5x2+4x= .
15.(2015 成都校级模拟)不等式(m﹣2)x>2﹣m的解集为x<﹣1,则m的取值范围是 .
16.(2015 武汉)如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元.
17.(2016 宝山区一模)如图,菱形ABCD的边长为10,sin∠BAC=,则对角线AC的长为 .
18.(2015 扬州)如图,已知Rt△ ( http: / / www.21cnjy.com )ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(第16题) (第17题) (第18题)
友情提示:请将选择题、填空题答案填写到第二卷上,只交第二卷.
初三数学月考试题
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题:
13._________ 14.__________15.___________
16._________ 17.__________18.___________
三.解答题(共66分)
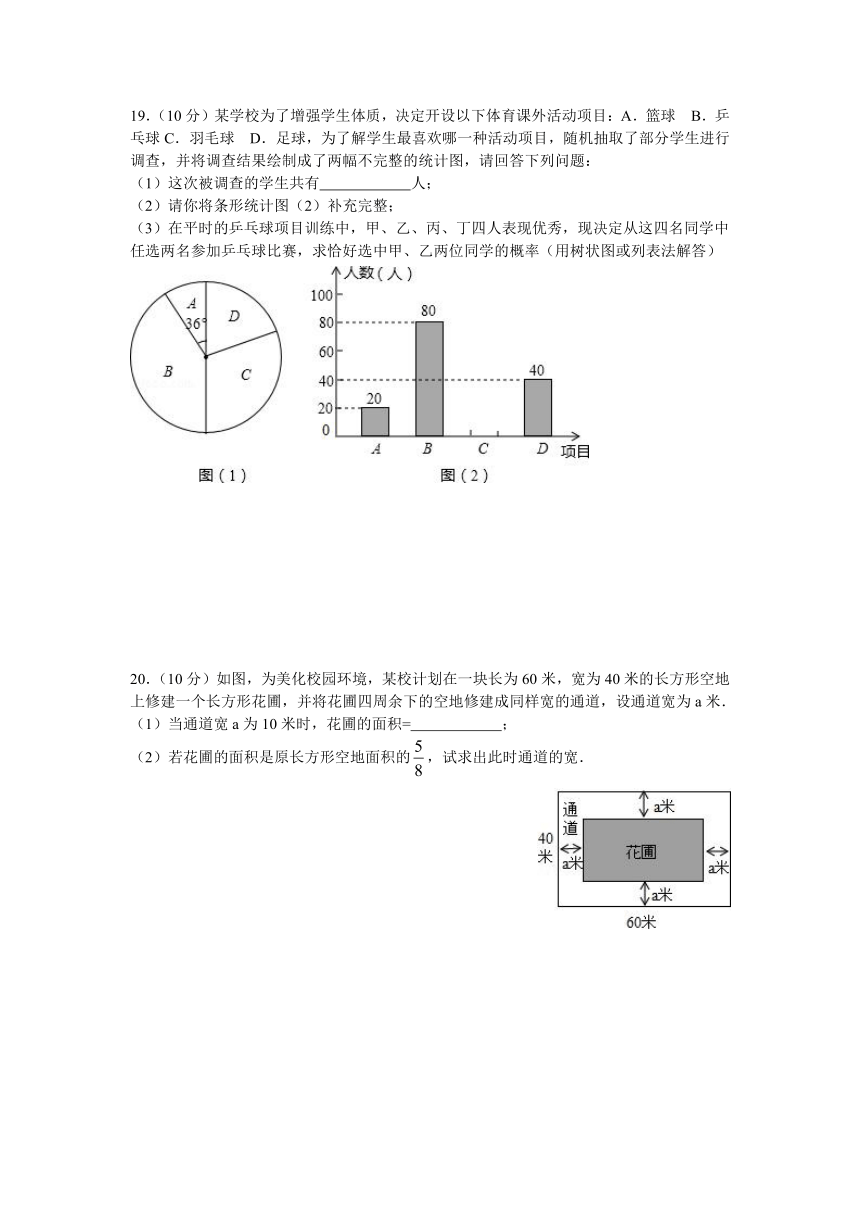
19.(10分)某学校为了增强学生体质,决 ( http: / / www.21cnjy.com )定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙 ( http: / / www.21cnjy.com )、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
( http: / / www.21cnjy.com )
20.(10分)如图,为美 ( http: / / www.21cnjy.com )化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)当通道宽a为10米时,花圃的面积= ;
(2)若花圃的面积是原长方形空地面积的,试求出此时通道的宽.
( http: / / www.21cnjy.com )
21.(10分)为了弘扬“社会主义核心 ( http: / / www.21cnjy.com )价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.
(1)求公益广告牌的高度AB;
(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号)
( http: / / www.21cnjy.com )
22.(12分)为了响应政府提出的 ( http: / / www.21cnjy.com )由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.
(1)求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本);
(2)当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?
23.(12分)如图,在梯形ABC ( http: / / www.21cnjy.com )D中,AD∥BC,∠A=∠ABC=90°,且AD=CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.
(1)求证:△DEF≌△CBF;
(2)判断四边形BCED是什么特殊四边形?说明理由;
(3)求∠ADC的度数.(直接写结论,不用证明)
( http: / / www.21cnjy.com )
24.(12分)如图,抛物线y=x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
( http: / / www.21cnjy.com )
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D B C A C A A A B D C
二、填空题:
13. __x=2_____ 14.__x(x-1)(x-4)___15._m<2______
16.___2_____ 17.___16_______18.__5______
三、解答题
19. 解:(1)根据题意得:20÷=200(人),
则这次被调查的学生共有200人;
(2)补全图形,如图所示:
( http: / / www.21cnjy.com )
(3)列表如下:
甲 乙 丙 丁
甲 ﹣﹣﹣ (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) ﹣﹣﹣ (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) ﹣﹣﹣ (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁) ﹣﹣﹣
所有等可能的结果为12种,其中符合要求的只有2种,
则P==.
20. 解:(1)由图可知,花圃的面积为:(40﹣2×10)(60﹣2×10)=800(平方米).
故答案为:800;
(2)根据题意得:
(40﹣2a)(60﹣2a)=×60×40,
解得:a1=5,a2=45(舍去).
答:此时通道的宽为5米.
21. 解:(1)在Rt△ADC中,∵∠ADC=60°,CD=3,
∵tan∠ADC=,
∴AC=3 tan60°=3,
在Rt△BDC中,∵∠BDC=45°,
∴BC=CD=3,
∴AB=AC﹣BC=(3﹣3)米.
(2)在Rt△ADC中,∵cos∠ADC=,
∴AD===6米,
在Rt△BDC中,∵cos∠BDC=,
∴BD===3米.
22. 解:(1)S=y(x﹣40)=(x﹣40)(﹣10x+1200)=﹣10x2+1600x﹣48000;
(2)S=﹣10x2+1600x﹣48000=﹣10(x﹣80)2+16000
则当销售单价定为80元时,工厂每天获得的利润最大,最大利润是16000元.
23. (1)证明:∵梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,
∴∠DFB=∠A=90°,AD=DF,
∵AD=CD,
∴DF=CD,
∴DF=CF,
∵AD∥BC,
∴∠FDE=∠FCB,
在△DEF和△CBF中,
∴△DEF≌△CBF;
(2)四边形BCED是菱形.
理由:∵△DEF≌△CBF,
∴DF=FC,EF=BF,
∴四边形BCED平行四边形,
在△DBF和△CFE中,
∴△DBF≌△CFE,
∴DB=DE,
∴四边形BCED是菱形.
(3)∠ADC=120°.
(∵折叠,∴∠ADB=∠CDB,
∵四边形BCED是菱形,
∴∠CDB=∠CDE,
∴∠ADB=∠CDB=∠CDE=60°,
∴∠ADC=120°.)
24. 解:(1)∵点A(﹣1,0)在抛物线上,
∴,
解得 ,
∴抛物线的解析式为.
∵,
∴顶点D的坐标为;
(2)△ABC是直角三角形.理由如下:
当x=0时,y=﹣2,
∴C(0,﹣2),则OC=2.
当y=0时,,
∴x1=﹣1,x2=4,则B(4,0),
∴OA=1,OB=4,
∴AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(3)由题意A、B两点关于对称轴对称,故直线BC与对称轴的交点即为点M.
由B(4,0),C(0,-2)
设直线BC:y=kx-2
4k-2=0,
k=.
所以直线BC:.
当时,.
所以M(,).
一.选择题(每小题3分,共36分)
1.(2016 南岗区一模)下列计算正确的是( )
A.2a+3a=6a B.a2 a3=a6 C.a8÷a4=a2 D.(﹣2a3)2=4a6
2.(2015 随州)若代数式+有意义,则实数x的取值范围是( )
A.x≠1 B.x≥0 C.x≠0 D.x≥0且x≠1
3.(2016 安徽模拟)2015年春运期间,全国有23.2亿人次进行
东西南北大流动,用科学记数法表示23.2亿是( )
A.23.2×108 B.2.32×109 C.232×107 D.2.32×108
4.(2015 攀枝花)如图所示的几何体为圆台,其俯视图正确的是( )
A. B. C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.(2015 庆阳)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. ( http: / / www.21cnjy.com ) D.
6.(2016 锦江区模拟)已知关于x的一元二次方程x2﹣2x﹣3=0
两实数根为x1、x2,则x1+x2的值是( )
A.3 B.﹣3 C.2 D.﹣2
7.(2016 安徽模拟)如图,等腰△ABC中,AB=AC=8,BC=5,
AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的
周长为( )
A.13 B.14 C.15 D.16
8.(2015 长沙县模拟)若2a﹣b=3,则9﹣4a+2b的值为( )
A.3 B.6 C.12 D.0
9.(2015 包头一模)若点P(2k﹣1,1﹣k)在第四象限,则k的取值范围为( )
A.k>1 B.k< C.k> D.<k<1
10.(2015 黔东南州)若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
11.(2015 乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
A. B. C. D.
12.(2016 深圳模拟)如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( )
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
A.1 B.2 C.3 D.4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(第11题) (第12题)
二.填空题(每小题3分,共18分)
13.(2015 德州)方程﹣=1的解是 .
14.(2015 昆山市一模)因式分解:x3﹣5x2+4x= .
15.(2015 成都校级模拟)不等式(m﹣2)x>2﹣m的解集为x<﹣1,则m的取值范围是 .
16.(2015 武汉)如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元.
17.(2016 宝山区一模)如图,菱形ABCD的边长为10,sin∠BAC=,则对角线AC的长为 .
18.(2015 扬州)如图,已知Rt△ ( http: / / www.21cnjy.com )ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(第16题) (第17题) (第18题)
友情提示:请将选择题、填空题答案填写到第二卷上,只交第二卷.
初三数学月考试题
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题:
13._________ 14.__________15.___________
16._________ 17.__________18.___________
三.解答题(共66分)
19.(10分)某学校为了增强学生体质,决 ( http: / / www.21cnjy.com )定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙 ( http: / / www.21cnjy.com )、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
( http: / / www.21cnjy.com )
20.(10分)如图,为美 ( http: / / www.21cnjy.com )化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)当通道宽a为10米时,花圃的面积= ;
(2)若花圃的面积是原长方形空地面积的,试求出此时通道的宽.
( http: / / www.21cnjy.com )
21.(10分)为了弘扬“社会主义核心 ( http: / / www.21cnjy.com )价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.
(1)求公益广告牌的高度AB;
(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号)
( http: / / www.21cnjy.com )
22.(12分)为了响应政府提出的 ( http: / / www.21cnjy.com )由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.
(1)求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本);
(2)当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?
23.(12分)如图,在梯形ABC ( http: / / www.21cnjy.com )D中,AD∥BC,∠A=∠ABC=90°,且AD=CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.
(1)求证:△DEF≌△CBF;
(2)判断四边形BCED是什么特殊四边形?说明理由;
(3)求∠ADC的度数.(直接写结论,不用证明)
( http: / / www.21cnjy.com )
24.(12分)如图,抛物线y=x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
( http: / / www.21cnjy.com )
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D B C A C A A A B D C
二、填空题:
13. __x=2_____ 14.__x(x-1)(x-4)___15._m<2______
16.___2_____ 17.___16_______18.__5______
三、解答题
19. 解:(1)根据题意得:20÷=200(人),
则这次被调查的学生共有200人;
(2)补全图形,如图所示:
( http: / / www.21cnjy.com )
(3)列表如下:
甲 乙 丙 丁
甲 ﹣﹣﹣ (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) ﹣﹣﹣ (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) ﹣﹣﹣ (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁) ﹣﹣﹣
所有等可能的结果为12种,其中符合要求的只有2种,
则P==.
20. 解:(1)由图可知,花圃的面积为:(40﹣2×10)(60﹣2×10)=800(平方米).
故答案为:800;
(2)根据题意得:
(40﹣2a)(60﹣2a)=×60×40,
解得:a1=5,a2=45(舍去).
答:此时通道的宽为5米.
21. 解:(1)在Rt△ADC中,∵∠ADC=60°,CD=3,
∵tan∠ADC=,
∴AC=3 tan60°=3,
在Rt△BDC中,∵∠BDC=45°,
∴BC=CD=3,
∴AB=AC﹣BC=(3﹣3)米.
(2)在Rt△ADC中,∵cos∠ADC=,
∴AD===6米,
在Rt△BDC中,∵cos∠BDC=,
∴BD===3米.
22. 解:(1)S=y(x﹣40)=(x﹣40)(﹣10x+1200)=﹣10x2+1600x﹣48000;
(2)S=﹣10x2+1600x﹣48000=﹣10(x﹣80)2+16000
则当销售单价定为80元时,工厂每天获得的利润最大,最大利润是16000元.
23. (1)证明:∵梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,
∴∠DFB=∠A=90°,AD=DF,
∵AD=CD,
∴DF=CD,
∴DF=CF,
∵AD∥BC,
∴∠FDE=∠FCB,
在△DEF和△CBF中,
∴△DEF≌△CBF;
(2)四边形BCED是菱形.
理由:∵△DEF≌△CBF,
∴DF=FC,EF=BF,
∴四边形BCED平行四边形,
在△DBF和△CFE中,
∴△DBF≌△CFE,
∴DB=DE,
∴四边形BCED是菱形.
(3)∠ADC=120°.
(∵折叠,∴∠ADB=∠CDB,
∵四边形BCED是菱形,
∴∠CDB=∠CDE,
∴∠ADB=∠CDB=∠CDE=60°,
∴∠ADC=120°.)
24. 解:(1)∵点A(﹣1,0)在抛物线上,
∴,
解得 ,
∴抛物线的解析式为.
∵,
∴顶点D的坐标为;
(2)△ABC是直角三角形.理由如下:
当x=0时,y=﹣2,
∴C(0,﹣2),则OC=2.
当y=0时,,
∴x1=﹣1,x2=4,则B(4,0),
∴OA=1,OB=4,
∴AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(3)由题意A、B两点关于对称轴对称,故直线BC与对称轴的交点即为点M.
由B(4,0),C(0,-2)
设直线BC:y=kx-2
4k-2=0,
k=.
所以直线BC:.
当时,.
所以M(,).
同课章节目录
