7.1.2两条直线垂直 课件(共24张PPT)
文档属性
| 名称 | 7.1.2两条直线垂直 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 21:56:52 | ||
图片预览








文档简介
(共24张PPT)
7.1.2 两条直线垂直
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1.了解垂线、垂线段等概念,能过一点作已知直线的垂线;理解点到直线的距离的意义,能度量点到直线的距离.
2.理解并掌握垂线的两个性质,能利用垂线的定义计算角的度数.
3.经历观察、操作 、探索、归纳 、总结的过程,初步形成几何概念的认识方式和几何结论的归纳方法.
新课导入
新课导入
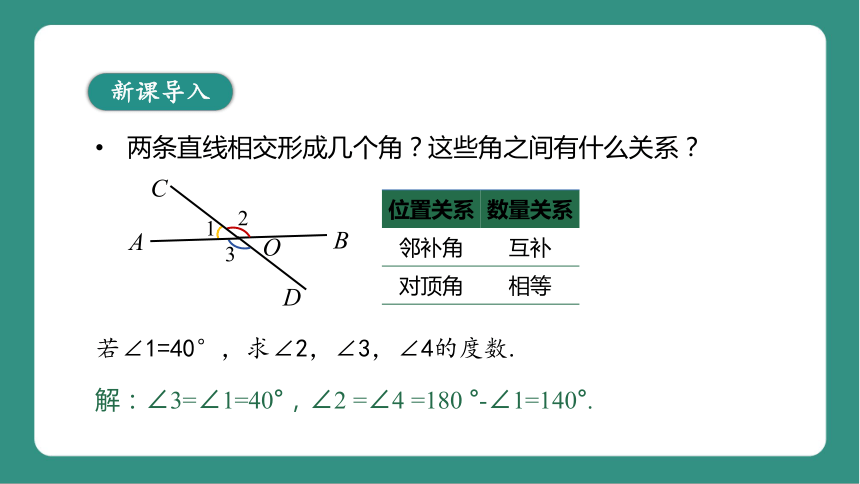
两条直线相交形成几个角?这些角之间有什么关系?
位置关系 数量关系
邻补角 互补
对顶角 相等
若∠1=40°,求∠2,∠3,∠4的度数.
解:∠3=∠1=40°,∠2 =∠4 =180 °-∠1=140°.
C
O
A
B
D
3
2
1
新课导入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
新知讲解
新知讲解
知识点 1
垂直、垂线、垂足的概念
如图,当∠AOC=90° 时,∠BOD,∠AOD,∠BOC 的度数是多少?
A
B
C
D
O
由对顶角和邻补角的性质可知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
新知讲解
知识点 1
垂直、垂线、垂足的概念
垂线:当两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
注意:两条直线互相垂直是它们相交的一种特殊情况.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
A
B
C
D
O
新知讲解
知识点 1
垂直、垂线、垂足的概念
垂直的表示方法:
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
如果用 l,m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
新知讲解
知识点 1
垂直、垂线、垂足的概念
垂直的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
A
B
C
D
O
l
m
新知讲解
知识点 2
垂线的画法及性质
(1)画已知直线l 的垂线能画几条
(2)过直线l上的一点A 画l 的垂线,这样的垂线能画几条
(3)过直线l外的一点B 画l 的垂线,这样的垂线能画几条
A
.B
l
.
(1)无数条
(2)有且只有一条
(3)有且只有一条
新知讲解
知识点 2
垂线的画法及性质
l
O
A
…
任务:观看动画演示,归纳经过一点画已知直线的垂线的通常画法.
新知讲解
知识点 2
垂线的画法及性质
归纳:“一落、二过、三画”:
“一落”是指把三角板的一条直角边落在已知直线上;
“二过”是指使三角板的另一条直角边过已知点;
“三画”是指沿已知点所在的直角边画直线.
总结:在同一平面内,过一点有且只有一条直线与已知直线垂直.
新知讲解
知识点 2
垂线的画法及性质
注意:
(1)不能忽略“在同一平面内”这个条件,∵ 如果不在同一平面内,那么过一点有无数条直线与已知直线垂直.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
新知讲解
知识点 3
点到直线的距离
运用直尺测量发现,线段PO 的长度最短.
这样的线段 PO 只有一条.
新知讲解
知识点 3
点到直线的距离
连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到
直线 l 的距离.
C
D
E
l
B
A
课后总结
课后总结
典例精析
考点1:利用垂直求角的度数
1.如图,AB⊥CD,垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等) .
课后总结
典例精析
考点1:利用垂直求角的度数
2. 如图,直线AB,CD相交于点O,OE⊥AB,∠AOD=125°,
求∠COE的度数.
解:∵∠AOD=125°,
又∵∠COB=∠AOD, ∴∠COB=125°.
∵OE⊥AB,∴∠EOB=90°.
∴∠COE=∠COB-∠EOB=125°-90°=35°.
课后总结
典例精析
考点2:画出点到直线的距离
4. 如图,火车站、码头分别位于 A,B 两点,直线 a 和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
A
a
B
b
课后总结
典例精析
考点3:存在性问题
5. 如图,直线 AB,CD 相交于点 O,∠AOC = 45°,∠AOD = 3∠DOE.图中是否存在互相垂直的直线?若存在,请写出互相垂直的直线;若不存在,请说明理由.
解:存在,OE⊥AB.理由如下:
∵ ∠AOC = 45°,∴ ∠AOD = 180°-∠AOC
= 180°-45° = 135°.
∵ ∠AOD =3∠DOE,∴ 3∠DOE = 135°,
∴ ∠DOE = 45°,∴ ∠AOE = ∠AOD-∠DOE =135°-45° = 90°,∴ OE⊥AB.
课后总结
典例精析
考点4:折叠问题
6. 将一张长方形纸片按如图5.1-12 所示方式折叠,EF,EG 为折痕,判断EF 与EG 的位置关系.
解题秘方:利用折叠的性质求出两线的夹角,根据夹角是90°判断两条直线的位置关系.
课后总结
典例精析
考点4:折叠问题
6. 将一张长方形纸片按如图5.1-12 所示方式折叠,EF,EG 为折痕,判断EF 与EG 的位置关系.
又∵ ∠A′EA+∠A′EB=180°,
∴∠FEG=∠A′EF+∠A′EG=
1/2 ∠ AEA′+ 1/2∠ A′EB= 1/2 (∠ AEA′+∠ A′EB)= 1/2 ×180°=90°.
∴EF ⊥ EG.(邻补角的平分线互相垂直.)
7.1.2 两条直线垂直
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1.了解垂线、垂线段等概念,能过一点作已知直线的垂线;理解点到直线的距离的意义,能度量点到直线的距离.
2.理解并掌握垂线的两个性质,能利用垂线的定义计算角的度数.
3.经历观察、操作 、探索、归纳 、总结的过程,初步形成几何概念的认识方式和几何结论的归纳方法.
新课导入
新课导入
两条直线相交形成几个角?这些角之间有什么关系?
位置关系 数量关系
邻补角 互补
对顶角 相等
若∠1=40°,求∠2,∠3,∠4的度数.
解:∠3=∠1=40°,∠2 =∠4 =180 °-∠1=140°.
C
O
A
B
D
3
2
1
新课导入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
新知讲解
新知讲解
知识点 1
垂直、垂线、垂足的概念
如图,当∠AOC=90° 时,∠BOD,∠AOD,∠BOC 的度数是多少?
A
B
C
D
O
由对顶角和邻补角的性质可知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
新知讲解
知识点 1
垂直、垂线、垂足的概念
垂线:当两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
注意:两条直线互相垂直是它们相交的一种特殊情况.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
A
B
C
D
O
新知讲解
知识点 1
垂直、垂线、垂足的概念
垂直的表示方法:
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
如果用 l,m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
新知讲解
知识点 1
垂直、垂线、垂足的概念
垂直的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
A
B
C
D
O
l
m
新知讲解
知识点 2
垂线的画法及性质
(1)画已知直线l 的垂线能画几条
(2)过直线l上的一点A 画l 的垂线,这样的垂线能画几条
(3)过直线l外的一点B 画l 的垂线,这样的垂线能画几条
A
.B
l
.
(1)无数条
(2)有且只有一条
(3)有且只有一条
新知讲解
知识点 2
垂线的画法及性质
l
O
A
…
任务:观看动画演示,归纳经过一点画已知直线的垂线的通常画法.
新知讲解
知识点 2
垂线的画法及性质
归纳:“一落、二过、三画”:
“一落”是指把三角板的一条直角边落在已知直线上;
“二过”是指使三角板的另一条直角边过已知点;
“三画”是指沿已知点所在的直角边画直线.
总结:在同一平面内,过一点有且只有一条直线与已知直线垂直.
新知讲解
知识点 2
垂线的画法及性质
注意:
(1)不能忽略“在同一平面内”这个条件,∵ 如果不在同一平面内,那么过一点有无数条直线与已知直线垂直.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
新知讲解
知识点 3
点到直线的距离
运用直尺测量发现,线段PO 的长度最短.
这样的线段 PO 只有一条.
新知讲解
知识点 3
点到直线的距离
连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到
直线 l 的距离.
C
D
E
l
B
A
课后总结
课后总结
典例精析
考点1:利用垂直求角的度数
1.如图,AB⊥CD,垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等) .
课后总结
典例精析
考点1:利用垂直求角的度数
2. 如图,直线AB,CD相交于点O,OE⊥AB,∠AOD=125°,
求∠COE的度数.
解:∵∠AOD=125°,
又∵∠COB=∠AOD, ∴∠COB=125°.
∵OE⊥AB,∴∠EOB=90°.
∴∠COE=∠COB-∠EOB=125°-90°=35°.
课后总结
典例精析
考点2:画出点到直线的距离
4. 如图,火车站、码头分别位于 A,B 两点,直线 a 和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
A
a
B
b
课后总结
典例精析
考点3:存在性问题
5. 如图,直线 AB,CD 相交于点 O,∠AOC = 45°,∠AOD = 3∠DOE.图中是否存在互相垂直的直线?若存在,请写出互相垂直的直线;若不存在,请说明理由.
解:存在,OE⊥AB.理由如下:
∵ ∠AOC = 45°,∴ ∠AOD = 180°-∠AOC
= 180°-45° = 135°.
∵ ∠AOD =3∠DOE,∴ 3∠DOE = 135°,
∴ ∠DOE = 45°,∴ ∠AOE = ∠AOD-∠DOE =135°-45° = 90°,∴ OE⊥AB.
课后总结
典例精析
考点4:折叠问题
6. 将一张长方形纸片按如图5.1-12 所示方式折叠,EF,EG 为折痕,判断EF 与EG 的位置关系.
解题秘方:利用折叠的性质求出两线的夹角,根据夹角是90°判断两条直线的位置关系.
课后总结
典例精析
考点4:折叠问题
6. 将一张长方形纸片按如图5.1-12 所示方式折叠,EF,EG 为折痕,判断EF 与EG 的位置关系.
又∵ ∠A′EA+∠A′EB=180°,
∴∠FEG=∠A′EF+∠A′EG=
1/2 ∠ AEA′+ 1/2∠ A′EB= 1/2 (∠ AEA′+∠ A′EB)= 1/2 ×180°=90°.
∴EF ⊥ EG.(邻补角的平分线互相垂直.)
同课章节目录
