7.1.3 两条直线被第三条直线所截 课件(共20张PPT)
文档属性
| 名称 | 7.1.3 两条直线被第三条直线所截 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 21:54:31 | ||
图片预览





文档简介
(共20张PPT)
7.1.3 两条直线被第三条直线所截
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1.理解同位角、内错角、同旁内角的概念,能结合具体图形识别同位角、内错角、同旁内角.
2.能从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.
3. 会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
新课导入
新课导入
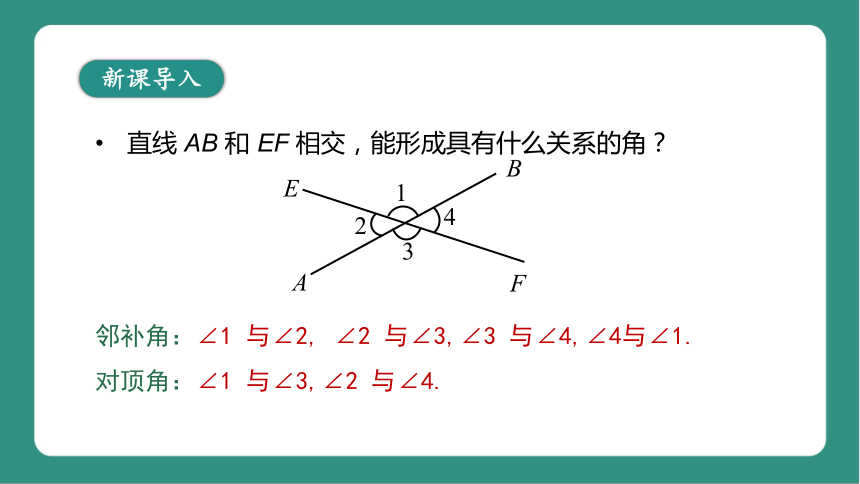
直线 AB 和 EF 相交,能形成具有什么关系的角?
邻补角:∠1 与∠2, ∠2 与∠3,∠3 与∠4,∠4与∠1.
对顶角:∠1 与∠3,∠2 与∠4.
B
A
F
E
1
4
2
3
新知讲解
新知讲解
知识点 1
同位角、内错角、同旁内角
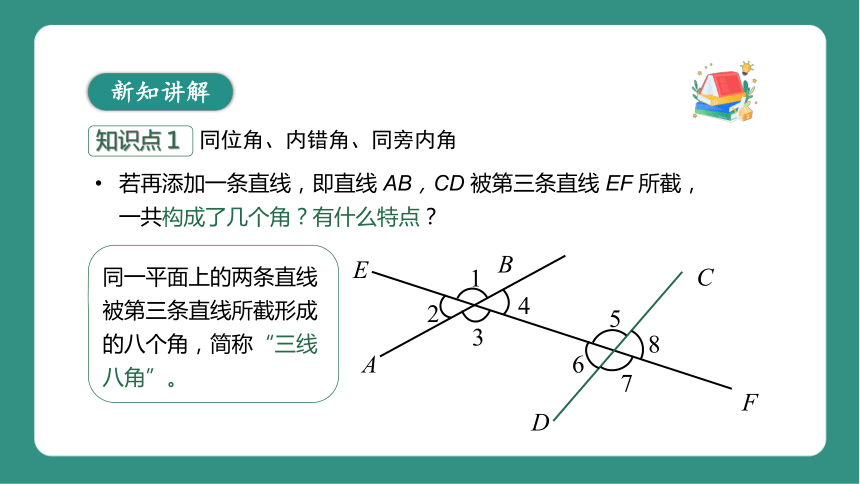
若再添加一条直线,即直线 AB,CD 被第三条直线 EF 所截,一共构成了几个角?有什么特点?
5
8
6
7
B
A
F
E
C
D
1
4
2
3
同一平面上的两条直线被第三条直线所截形成的八个角,简称“三线八角”。
新知讲解
知识点 1
同位角、内错角、同旁内角
F
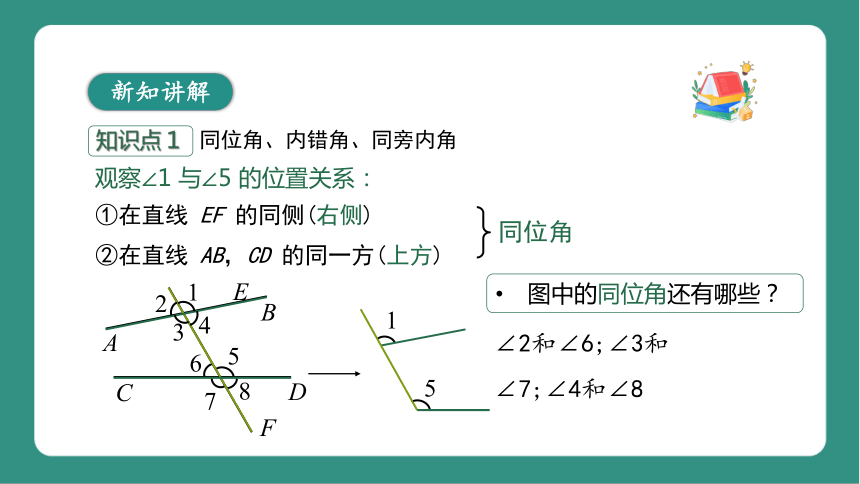
观察∠1 与∠5 的位置关系:
①在直线 EF 的同侧(右侧)
②在直线 AB,CD 的同一方(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
新知讲解
知识点 1
同位角、内错角、同旁内角
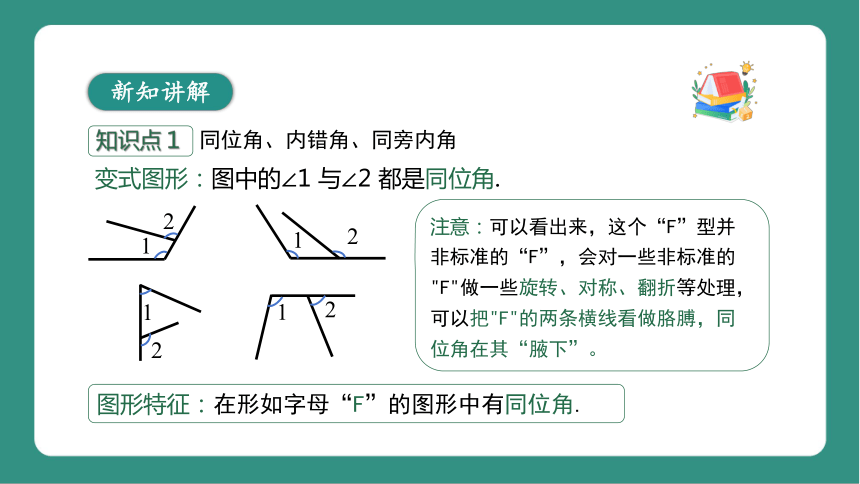
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1 与∠2 都是同位角.
1
1
2
1
2
1
2
2
注意:可以看出来,这个“F”型并非标准的“F”,会对一些非标准的"F"做一些旋转、对称、翻折等处理,可以把"F"的两条横线看做胳膊,同位角在其“腋下”。
新知讲解
知识点 1
同位角、内错角、同旁内角
观察∠3 与∠5 的位置关系:
①分别在直线 EF 的两侧
②在直线 AB,CD 之间
内错角
8
A
C
B
D
E
F
1
2
3
4
5
6
7
3
5
∠4 和∠6
图中的内错角还有哪些?
新知讲解
知识点 1
同位角、内错角、同旁内角
1
2
1
1
1
2
2
2
变式图形:图中的∠1 与∠2 都是同位角.
图形特征:在形如字母“Z”的图形中有同位角.
注意:这些“Z”字型也不是标准的“Z”字型,在它的内部形成的两个角就为内错角。
新知讲解
知识点 1
同位角、内错角、同旁内角
观察∠4 与∠5 的位置关系:
①在直线 EF 的同一旁(右侧)
②在直线 AB,CD 之间
同旁内角
4
5
8
A
C
B
D
E
F
1
2
3
4
5
6
7
∠3 和∠6
图中的同旁内角还有哪些?
新知讲解
知识点 1
同位角、内错角、同旁内角
变式图形:图中的∠1 与∠2 都是同位角.
1
1
1
1
2
2
2
2
图形特征:在形如字母“C”的图形中有同位角.
注意:这些也是非标准的“U”字,在出现的时候大家要能快速识别。
新知讲解
知识点 1
同位角、内错角、同旁内角
注意:
(1)同位角、内错角、同旁内角都是指两个角之间的位置关系,不是大小关系,它们之间的大小关系都是不确定的.
(2)同位角、内错角、同旁内角都是成对出现的,它们都没有公共顶点,但都有一条边共线.
新知讲解
知识点 1
同位角、内错角、同旁内角
判断三线八角的方法
1.把两个角在图中描画出来;
2.找到两个角的公共直线;
3.观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
课后总结
课后总结
数学归纳
同位角、内错角、同旁内角的特征
角的名称 位置特征 基本图形 结构特征 相同点 共同特征
同位角
同旁 内角 内错角 F
Z
U
1
2
1
2
1
2
都在截线同侧
都没有公共顶点
都在被截线之间
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
课后总结
典例精析
考点1:同位角、内错角、同旁内角的综合识别
如图,直线 DE,BC 被直线 AB 所截. (1) ∠1 和∠2, ∠1 和∠3,∠1 和∠4 各是什么位置关系的角?(2)如果∠1 =∠4,那么∠1 和∠2 相等吗?∠1 和∠3 互补吗?为什么?
解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角.(2)如果∠1 =∠4,由对顶角相等,得∠2 =∠4,那么∠1 =∠2.因为∠3 和∠4 互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠1+∠3=180°,即∠1和∠3互补.
拓展延伸
拓展延伸
三线八角手势记忆法
同位角
内错角
同旁内角
7.1.3 两条直线被第三条直线所截
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1.理解同位角、内错角、同旁内角的概念,能结合具体图形识别同位角、内错角、同旁内角.
2.能从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想.
3. 会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
新课导入
新课导入
直线 AB 和 EF 相交,能形成具有什么关系的角?
邻补角:∠1 与∠2, ∠2 与∠3,∠3 与∠4,∠4与∠1.
对顶角:∠1 与∠3,∠2 与∠4.
B
A
F
E
1
4
2
3
新知讲解
新知讲解
知识点 1
同位角、内错角、同旁内角
若再添加一条直线,即直线 AB,CD 被第三条直线 EF 所截,一共构成了几个角?有什么特点?
5
8
6
7
B
A
F
E
C
D
1
4
2
3
同一平面上的两条直线被第三条直线所截形成的八个角,简称“三线八角”。
新知讲解
知识点 1
同位角、内错角、同旁内角
F
观察∠1 与∠5 的位置关系:
①在直线 EF 的同侧(右侧)
②在直线 AB,CD 的同一方(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
新知讲解
知识点 1
同位角、内错角、同旁内角
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1 与∠2 都是同位角.
1
1
2
1
2
1
2
2
注意:可以看出来,这个“F”型并非标准的“F”,会对一些非标准的"F"做一些旋转、对称、翻折等处理,可以把"F"的两条横线看做胳膊,同位角在其“腋下”。
新知讲解
知识点 1
同位角、内错角、同旁内角
观察∠3 与∠5 的位置关系:
①分别在直线 EF 的两侧
②在直线 AB,CD 之间
内错角
8
A
C
B
D
E
F
1
2
3
4
5
6
7
3
5
∠4 和∠6
图中的内错角还有哪些?
新知讲解
知识点 1
同位角、内错角、同旁内角
1
2
1
1
1
2
2
2
变式图形:图中的∠1 与∠2 都是同位角.
图形特征:在形如字母“Z”的图形中有同位角.
注意:这些“Z”字型也不是标准的“Z”字型,在它的内部形成的两个角就为内错角。
新知讲解
知识点 1
同位角、内错角、同旁内角
观察∠4 与∠5 的位置关系:
①在直线 EF 的同一旁(右侧)
②在直线 AB,CD 之间
同旁内角
4
5
8
A
C
B
D
E
F
1
2
3
4
5
6
7
∠3 和∠6
图中的同旁内角还有哪些?
新知讲解
知识点 1
同位角、内错角、同旁内角
变式图形:图中的∠1 与∠2 都是同位角.
1
1
1
1
2
2
2
2
图形特征:在形如字母“C”的图形中有同位角.
注意:这些也是非标准的“U”字,在出现的时候大家要能快速识别。
新知讲解
知识点 1
同位角、内错角、同旁内角
注意:
(1)同位角、内错角、同旁内角都是指两个角之间的位置关系,不是大小关系,它们之间的大小关系都是不确定的.
(2)同位角、内错角、同旁内角都是成对出现的,它们都没有公共顶点,但都有一条边共线.
新知讲解
知识点 1
同位角、内错角、同旁内角
判断三线八角的方法
1.把两个角在图中描画出来;
2.找到两个角的公共直线;
3.观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
课后总结
课后总结
数学归纳
同位角、内错角、同旁内角的特征
角的名称 位置特征 基本图形 结构特征 相同点 共同特征
同位角
同旁 内角 内错角 F
Z
U
1
2
1
2
1
2
都在截线同侧
都没有公共顶点
都在被截线之间
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
课后总结
典例精析
考点1:同位角、内错角、同旁内角的综合识别
如图,直线 DE,BC 被直线 AB 所截. (1) ∠1 和∠2, ∠1 和∠3,∠1 和∠4 各是什么位置关系的角?(2)如果∠1 =∠4,那么∠1 和∠2 相等吗?∠1 和∠3 互补吗?为什么?
解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角.(2)如果∠1 =∠4,由对顶角相等,得∠2 =∠4,那么∠1 =∠2.因为∠3 和∠4 互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠1+∠3=180°,即∠1和∠3互补.
拓展延伸
拓展延伸
三线八角手势记忆法
同位角
内错角
同旁内角
同课章节目录
