7.2.3 平行线的性质(第一课时) 课件(共37张PPT)
文档属性
| 名称 | 7.2.3 平行线的性质(第一课时) 课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 22:02:13 | ||
图片预览









文档简介
(共37张PPT)
7.2.3 平行线的性质
第一课时
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能熟练运用平行线的性质进行简单的推理证明.
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力,已知平行用性质,要证平行用判定.
新课导入
新课导入
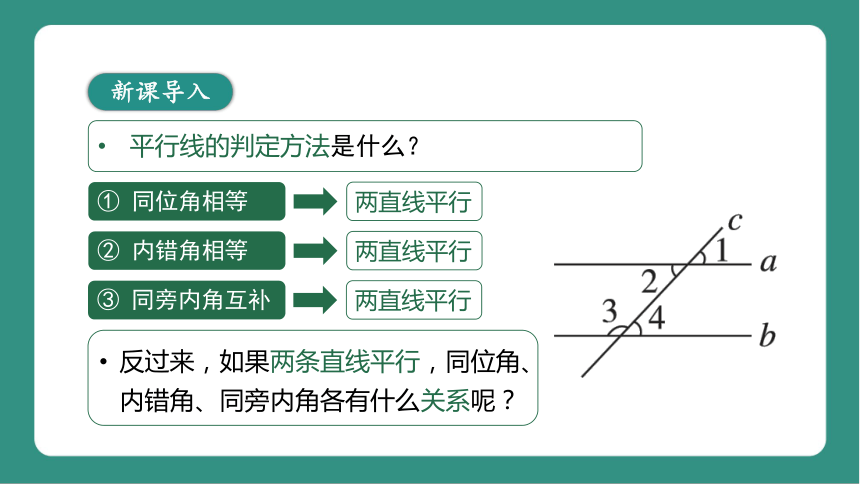
平行线的判定方法是什么?
① 同位角相等
两直线平行
② 内错角相等
两直线平行
③ 同旁内角互补
两直线平行
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
新知讲解
新知讲解
知识点 1
两直线平行,同位角相等
如图,直线a与直线b平行.
(1)测量同位角∠1和∠5的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
相等:∠1=∠5,
∠2=∠6,
∠3=∠7,
∠4=∠8 .
在画图过程中,三角尺起着什么样的作用
解:使∠1=∠2.
新知讲解
知识点 1
两直线平行,同位角相等
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
所以∠1=∠2
(两直线平行,同位角相等)
因为a∥b(已知)
几何语言:
新知讲解
知识点 1
两直线平行,同位角相等
【新课标·深入研究】如果∠1 ≠ ∠2,AB与CD的位置关系会怎样呢?
A
B
C
D
E
M
N
G
H
1
2
证明:假设∠1 ≠ ∠2,那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
根据“同位角相等,两直线平行”,可知GH ∥ CD.
又因为AB ∥ CD,这样经过点M存在两条直线AB和GH都与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2的假设不成立,所以∠1 =∠2.
新知讲解
知识点 1
两直线平行,同位角相等
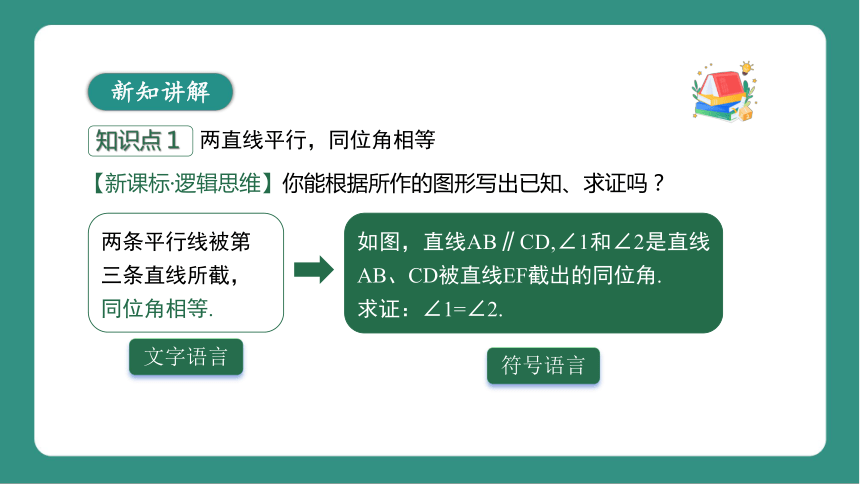
【新课标·逻辑思维】你能根据所作的图形写出已知、求证吗?
文字语言
两条平行线被第三条直线所截,同位角相等.
如图,直线AB∥CD,∠1和∠2是直线AB、CD被直线EF截出的同位角.
求证:∠1=∠2.
符号语言
新知讲解
知识点 2
两直线平行,内错角相等
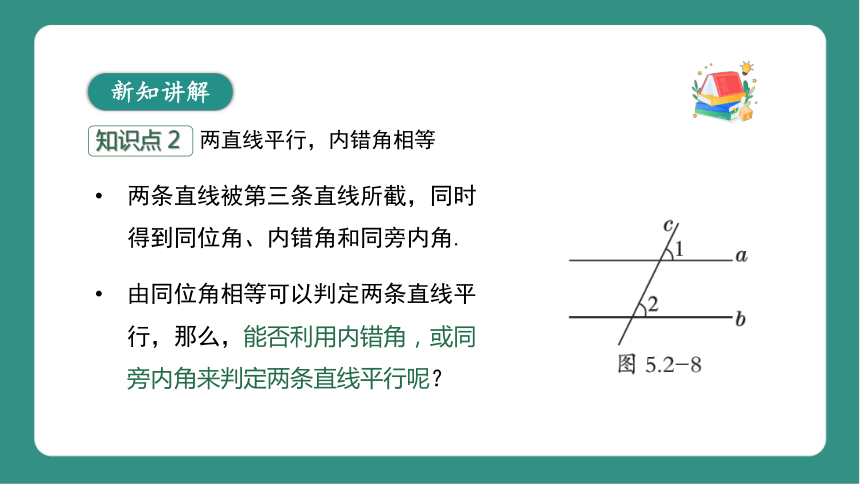
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角.
由同位角相等可以判定两条直线平行,那么,能否利用内错角,或同旁内角来判定两条直线平行呢?
新知讲解
知识点 2
两直线平行,内错角相等
如图,直线a与直线b平行.
(2)图中有几对内错角?它们的大小有什么关系?为什么?
有两对内错角:
∠3=∠6、
∠4=∠5;
因为∠3=∠7, ∠7= ∠6,
同理: ∠4=∠5.
所以∠3=∠6.
说明:
新知讲解
知识点 2
两直线平行,内错角相等
一般地,平行线具有性质:
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
所以∠2=∠3
(两直线平行,内错角相等)
因为a∥b(已知)
几何语言:
新知讲解
知识点 2
两直线平行,内错角相等
1.如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.
所以∠ 2= 50° (等量代换).
解:因为 a∥b(已知),
所以∠ 1= ∠ 2
(两直线平行,内错角相等).
又因为∠ 1 = 50° (已知),
新知讲解
知识点 3
两直线平行,同旁内角互补
如图,直线a与直线b平行.
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
有两对同旁内角:
∠3+∠5=180°,
∠4+∠6=180°.
说明:因为∠1=∠5, ∠3 + ∠1 =180°,
所以∠3+∠5=180°.
新知讲解
知识点 3
两直线平行,同旁内角互补
一般地,平行线具有如下性质:
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
所以∠2+∠4=180°
(两直线平行,同旁内角互补)
因为a∥b(已知)
几何语言:
新知讲解
知识点 3
两直线平行,同旁内角互补
2.如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
解:因为梯形上、下底互相平行,
所以∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°,65°.
于是∠D=180 °-∠A=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.
新知讲解
知识点 3
两直线平行,同旁内角互补
3.如图所示,直线a∥b,直线l与a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为 ( )
A. 58° B. 42°
C. 32° D. 28°
C
课后总结
课后总结
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
课后总结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
课后总结
性质 文字语言 符号语言 图示
性质1 两直线平行,同位角相等 如果 a//b, 那么∠1=∠2
性质2 两直线平行,内错角相等 如果 a//b, 那么∠2=∠3 性质3 两直线平行,同旁内角互补 如果 a//b, 那么∠2+∠4=180° 数学归纳
平行线的性质
课后总结
典例精析
考点1:两直线平行,同位角相等的综合应用
1.如图,AB//CD,BC//AE,∠1 =50°,求∠A,∠B,∠C 的度数.
解:∵ AB//CD,∴∠A=∠1=50°.
∵BC//AE,
∴ ∠C=∠1=50°, ∠A +∠B= 180°
∴ ∠B=180°-∠A= 130°.
课后总结
典例精析
考点2:两直线平行,内错角相等的综合应用
2.如图,在 A,B 两地之间要修一条笔直的公路,从 A 地测得公路走向是北偏东 48°,A,B 两地同时开工,若干天后公路准确接通.
(1)从 B 地测得公路的走向是南偏西多少度
解:(1)根据两直线平行,内错角相等,
可得∠ABG=48°,
∴ 从 B 地测得公路的走向是南偏西 48°.
课后总结
典例精析
考点3:两直线平行,同旁内角互补的综合应用
3.如图,AB//CD,直线 EF 分别交 AB,CD 于 M,N 两点,将一个含有 45°角的直角三角尺按如图所示的方式摆放,若∠EMB =75°,则∠PNM = .
30°
∠DNM=∠EMB =75°
∠PNM=∠DNM-∠DNP=30°
课后总结
典例精析
考点4:利用平行线的性质求角的度数
解析:∵ 直尺的两边互相平行,∠1=35°,
∴ ∠3=35°.∵ ∠2+∠3+90°=180°,∴∠2=55°.
4.如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45°
C.55° D.65°
C
课后总结
典例精析
考点5:以折叠为背景求角度数
解:由题意得 AD//BC,
∴∠GFE =∠1,∠DFE +∠1=180°,
又∠1=55°,∴∠GFE =55°,
∠DFE =180° -55°=125°.
由折叠的性质,可得∠D'FE=∠DFE=125°,
∴∠2=∠D'FE-∠GFE=125°- 55°=70° .
5.如图,将一张长方形纸片 ABCD 沿 EF 折叠后,C,D 两点分别落在点 C ′,D′的位置,C′E 交 AF 于点 G,测得∠1=55°,求∠2 的度数.
课后总结
典例精析
考点6:借助学具特征求角度数
6.将一个直角三角尺与两边平行的纸条如图放置,则下列结论正确的是(填序号)__________.
① ∠1=∠2; ② ∠4+∠5=180°;
③ ∠1+∠4=90°; ④ ∠4+90°=∠3.
①②③④
拓展延伸
7.如图,已知EF//CD,GD//CA,∠1=140°.
拓展延伸
典例精析
考点4: 进阶 · 利用平行线的性质求角的度数
(1)求∠2的度数;
(2)若DG平分∠CDB,求∠A的度数.
解:(1)因为EF//CD,所以∠1+∠ACD=180°.
因为∠1=140°,所以∠ACD=40°.
因为GD//CA,所以∠2=∠ACD=40°.
(2)因为DG平分∠CDB,∠2=40°,
所以∠BDG=∠2=40°.
因为GD//CA,所以∠A=∠BDG=40°
8.如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=40°,则∠2=( )
拓展延伸
典例精析
考点4: 进阶 · 利用平行线的性质求角的度数
A.35° B.40°
C.45° D.50°
D
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
9.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是 .
解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
180°﹣3α.
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
9.如图,把一张长方形纸片ABCD沿EF折叠后,点A与点A′重合(点A在BC边上),点B落在点B′的位置上,若∠DEA′=40°,则∠1+∠2= °.
120
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
9.详解:
解:∵AD∥BC,∠DEA′=40°,
∴∠EA'F=40°,
又∵∠B'A'E=∠BAD=90°,
∴∠2=90°﹣40°=50°,
由折叠可得,∠1=
∠AEA'=
(180°﹣∠DEA')=
∴∠1+∠2=70°+50°=120°.
70°
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
10.【2018·衢州】如图,将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110°
C.108° D.106°
D
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
10.详解:
解:由折叠可得:∠DGH=∠HGE=×(180°-32°)=74°,再根据AD∥BC,即可得到∠GHC=180°-∠DGH=106°.故选D.
拓展延伸
典例精析
考点6: 进阶 · 借助学具特征求角度数
11.【2017·枣庄】如图,将一副三角尺和一张对边平行的纸条按下列方式摆放,两个三角尺的一直角边重合,含30°角的直角三角尺的斜边与纸条一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是
( )
A.15° B.22.5°
C.30° D.45°
A
7.2.3 平行线的性质
第一课时
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能熟练运用平行线的性质进行简单的推理证明.
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力,已知平行用性质,要证平行用判定.
新课导入
新课导入
平行线的判定方法是什么?
① 同位角相等
两直线平行
② 内错角相等
两直线平行
③ 同旁内角互补
两直线平行
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
新知讲解
新知讲解
知识点 1
两直线平行,同位角相等
如图,直线a与直线b平行.
(1)测量同位角∠1和∠5的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
相等:∠1=∠5,
∠2=∠6,
∠3=∠7,
∠4=∠8 .
在画图过程中,三角尺起着什么样的作用
解:使∠1=∠2.
新知讲解
知识点 1
两直线平行,同位角相等
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
所以∠1=∠2
(两直线平行,同位角相等)
因为a∥b(已知)
几何语言:
新知讲解
知识点 1
两直线平行,同位角相等
【新课标·深入研究】如果∠1 ≠ ∠2,AB与CD的位置关系会怎样呢?
A
B
C
D
E
M
N
G
H
1
2
证明:假设∠1 ≠ ∠2,那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
根据“同位角相等,两直线平行”,可知GH ∥ CD.
又因为AB ∥ CD,这样经过点M存在两条直线AB和GH都与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2的假设不成立,所以∠1 =∠2.
新知讲解
知识点 1
两直线平行,同位角相等
【新课标·逻辑思维】你能根据所作的图形写出已知、求证吗?
文字语言
两条平行线被第三条直线所截,同位角相等.
如图,直线AB∥CD,∠1和∠2是直线AB、CD被直线EF截出的同位角.
求证:∠1=∠2.
符号语言
新知讲解
知识点 2
两直线平行,内错角相等
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角.
由同位角相等可以判定两条直线平行,那么,能否利用内错角,或同旁内角来判定两条直线平行呢?
新知讲解
知识点 2
两直线平行,内错角相等
如图,直线a与直线b平行.
(2)图中有几对内错角?它们的大小有什么关系?为什么?
有两对内错角:
∠3=∠6、
∠4=∠5;
因为∠3=∠7, ∠7= ∠6,
同理: ∠4=∠5.
所以∠3=∠6.
说明:
新知讲解
知识点 2
两直线平行,内错角相等
一般地,平行线具有性质:
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
所以∠2=∠3
(两直线平行,内错角相等)
因为a∥b(已知)
几何语言:
新知讲解
知识点 2
两直线平行,内错角相等
1.如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.
所以∠ 2= 50° (等量代换).
解:因为 a∥b(已知),
所以∠ 1= ∠ 2
(两直线平行,内错角相等).
又因为∠ 1 = 50° (已知),
新知讲解
知识点 3
两直线平行,同旁内角互补
如图,直线a与直线b平行.
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
有两对同旁内角:
∠3+∠5=180°,
∠4+∠6=180°.
说明:因为∠1=∠5, ∠3 + ∠1 =180°,
所以∠3+∠5=180°.
新知讲解
知识点 3
两直线平行,同旁内角互补
一般地,平行线具有如下性质:
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
所以∠2+∠4=180°
(两直线平行,同旁内角互补)
因为a∥b(已知)
几何语言:
新知讲解
知识点 3
两直线平行,同旁内角互补
2.如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
解:因为梯形上、下底互相平行,
所以∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°,65°.
于是∠D=180 °-∠A=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.
新知讲解
知识点 3
两直线平行,同旁内角互补
3.如图所示,直线a∥b,直线l与a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为 ( )
A. 58° B. 42°
C. 32° D. 28°
C
课后总结
课后总结
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
课后总结
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
课后总结
性质 文字语言 符号语言 图示
性质1 两直线平行,同位角相等 如果 a//b, 那么∠1=∠2
性质2 两直线平行,内错角相等 如果 a//b, 那么∠2=∠3 性质3 两直线平行,同旁内角互补 如果 a//b, 那么∠2+∠4=180° 数学归纳
平行线的性质
课后总结
典例精析
考点1:两直线平行,同位角相等的综合应用
1.如图,AB//CD,BC//AE,∠1 =50°,求∠A,∠B,∠C 的度数.
解:∵ AB//CD,∴∠A=∠1=50°.
∵BC//AE,
∴ ∠C=∠1=50°, ∠A +∠B= 180°
∴ ∠B=180°-∠A= 130°.
课后总结
典例精析
考点2:两直线平行,内错角相等的综合应用
2.如图,在 A,B 两地之间要修一条笔直的公路,从 A 地测得公路走向是北偏东 48°,A,B 两地同时开工,若干天后公路准确接通.
(1)从 B 地测得公路的走向是南偏西多少度
解:(1)根据两直线平行,内错角相等,
可得∠ABG=48°,
∴ 从 B 地测得公路的走向是南偏西 48°.
课后总结
典例精析
考点3:两直线平行,同旁内角互补的综合应用
3.如图,AB//CD,直线 EF 分别交 AB,CD 于 M,N 两点,将一个含有 45°角的直角三角尺按如图所示的方式摆放,若∠EMB =75°,则∠PNM = .
30°
∠DNM=∠EMB =75°
∠PNM=∠DNM-∠DNP=30°
课后总结
典例精析
考点4:利用平行线的性质求角的度数
解析:∵ 直尺的两边互相平行,∠1=35°,
∴ ∠3=35°.∵ ∠2+∠3+90°=180°,∴∠2=55°.
4.如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45°
C.55° D.65°
C
课后总结
典例精析
考点5:以折叠为背景求角度数
解:由题意得 AD//BC,
∴∠GFE =∠1,∠DFE +∠1=180°,
又∠1=55°,∴∠GFE =55°,
∠DFE =180° -55°=125°.
由折叠的性质,可得∠D'FE=∠DFE=125°,
∴∠2=∠D'FE-∠GFE=125°- 55°=70° .
5.如图,将一张长方形纸片 ABCD 沿 EF 折叠后,C,D 两点分别落在点 C ′,D′的位置,C′E 交 AF 于点 G,测得∠1=55°,求∠2 的度数.
课后总结
典例精析
考点6:借助学具特征求角度数
6.将一个直角三角尺与两边平行的纸条如图放置,则下列结论正确的是(填序号)__________.
① ∠1=∠2; ② ∠4+∠5=180°;
③ ∠1+∠4=90°; ④ ∠4+90°=∠3.
①②③④
拓展延伸
7.如图,已知EF//CD,GD//CA,∠1=140°.
拓展延伸
典例精析
考点4: 进阶 · 利用平行线的性质求角的度数
(1)求∠2的度数;
(2)若DG平分∠CDB,求∠A的度数.
解:(1)因为EF//CD,所以∠1+∠ACD=180°.
因为∠1=140°,所以∠ACD=40°.
因为GD//CA,所以∠2=∠ACD=40°.
(2)因为DG平分∠CDB,∠2=40°,
所以∠BDG=∠2=40°.
因为GD//CA,所以∠A=∠BDG=40°
8.如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=40°,则∠2=( )
拓展延伸
典例精析
考点4: 进阶 · 利用平行线的性质求角的度数
A.35° B.40°
C.45° D.50°
D
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
9.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是 .
解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
180°﹣3α.
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
9.如图,把一张长方形纸片ABCD沿EF折叠后,点A与点A′重合(点A在BC边上),点B落在点B′的位置上,若∠DEA′=40°,则∠1+∠2= °.
120
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
9.详解:
解:∵AD∥BC,∠DEA′=40°,
∴∠EA'F=40°,
又∵∠B'A'E=∠BAD=90°,
∴∠2=90°﹣40°=50°,
由折叠可得,∠1=
∠AEA'=
(180°﹣∠DEA')=
∴∠1+∠2=70°+50°=120°.
70°
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
10.【2018·衢州】如图,将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110°
C.108° D.106°
D
拓展延伸
典例精析
考点5: 进阶 · 以折叠为背景求角度数
10.详解:
解:由折叠可得:∠DGH=∠HGE=×(180°-32°)=74°,再根据AD∥BC,即可得到∠GHC=180°-∠DGH=106°.故选D.
拓展延伸
典例精析
考点6: 进阶 · 借助学具特征求角度数
11.【2017·枣庄】如图,将一副三角尺和一张对边平行的纸条按下列方式摆放,两个三角尺的一直角边重合,含30°角的直角三角尺的斜边与纸条一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是
( )
A.15° B.22.5°
C.30° D.45°
A
同课章节目录
