7.2.3 平行线的性质(第二课时) 课件(共43张PPT)
文档属性
| 名称 | 7.2.3 平行线的性质(第二课时) 课件(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-22 00:00:00 | ||
图片预览










文档简介
(共43张PPT)
7.2.3 平行线的性质
第二课时
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1.掌握平行线的性质与判定的区别与联系,发展推理意识,能够理解数学基本概念之间的联系.
2.会能综合运用平行线的性质与判定进行推理和计算,锻炼识图能力,会对已有条件进行归纳与转化,提升应用能力.
3.通过对平行线的性质与判定的运用,培养数学语言表达能力,发展应用意识和决策能力.
新课导入
新课导入
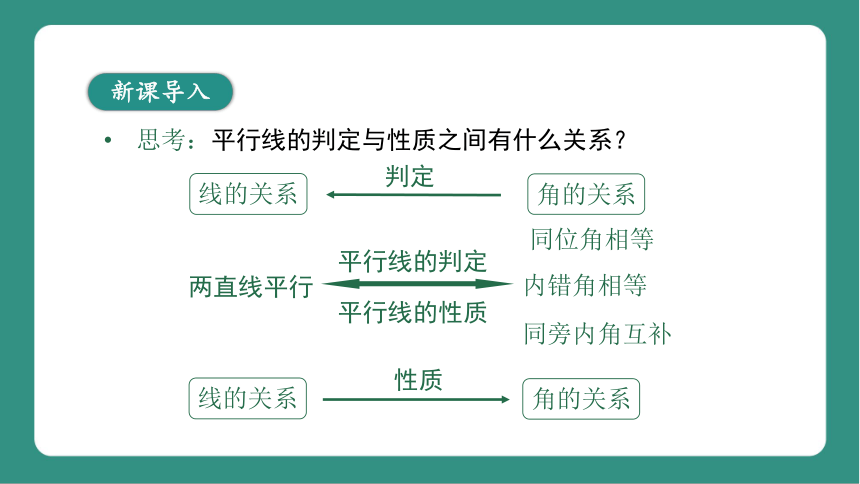
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
思考:平行线的判定与性质之间有什么关系?
新课导入
性质 文字语言 符号语言 图示
性质1 两直线平行,同位角相等 如果 a//b, 那么∠1=∠2
性质2 两直线平行,内错角相等 如果 a//b, 那么∠2=∠3 性质3 两直线平行,同旁内角互补 如果 a//b, 那么∠2+∠4=180° 思考:上节课我们学行线的哪些性质?
新知讲解
新知讲解
知识点 1
平行线性质和判定的综合应用
解:(1) DE∥BC. 理由如下:
∵ ∠ADE=60°,∠B = 60°,
∴ ∠ADE=∠B.
∴ DE∥BC. (同位角相等,两直线平行)
1. 如图,在三角形 ABC 中,D 是 AB 上一点,E 是 AC 上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(1) DE 和 BC 平行吗?为什么?
新知讲解
知识点 1
平行线性质和判定的综合应用
1. 如图,在三角形 ABC 中,D 是 AB 上一点,E 是 AC 上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(2)∠C 是多少度?为什么?
解:(2) ∠C =40°. 理由如下:
由(1)得 DE∥BC,
∴ ∠C=∠AED. (两直线平行,同位角相等)
又∵∠AED=40°,
∴ ∠C=∠AED =40°.
新知讲解
知识点 1
平行线性质和判定的综合应用
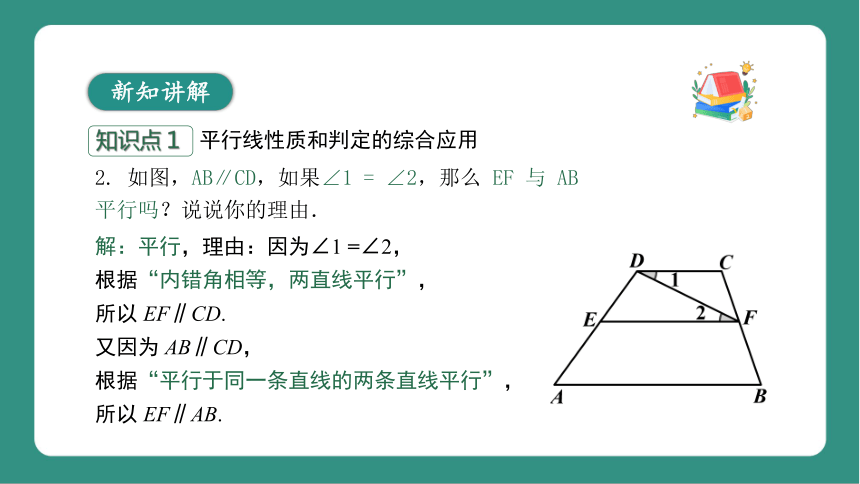
2. 如图,AB∥CD,如果∠1 = ∠2,那么 EF 与 AB
平行吗?说说你的理由.
解:平行,理由:因为∠1 =∠2,
根据“内错角相等,两直线平行”,
所以 EF∥CD.
又因为 AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以 EF∥AB.
新知讲解
知识点 1
平行线性质和判定的综合应用
3. 如图,已知直线 a∥b,直线 c∥d,∠1 = 107°,求∠2,∠3 的度数.
解:因为 a∥b,
所以 ∠1+∠3 = 180°,所以∠3 = 73°.
根据“两直线平行,内错角相等”,
所以 ∠2 =∠1 = 107°.
因为 c∥d,
根据“两直线平行,同旁内角互补”,
新知讲解
知识点 1
平行线性质和判定的综合应用
4. 如图 1,DB∥FG∥EC,∠ABD = 60°,∠ACE = 40°,AP 平分∠BAC.(1)求∠BAG的度数.(2)求∠PAG的度数.
新知讲解
知识点 2
添加辅助线的证明题
B
D
C
E
A
解:如图,过点 E 作 EF//AB.
∴∠B=∠BEF.
∵AB//CD,∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF =∠DEB,
即∠B+∠D=∠DEB.
F
5. 如图,若 AB//CD,你能确定∠B、∠D 与∠BED 之间的关系吗?说说你的看法.
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,AB∥CD,则:
性质1:当AB与CD之间有一个拐点时:∠A+∠C= ∠E.
性质2:当AB与CD之间有两个拐点时:∠A+∠F= ∠E +∠D.
性质3:当AB与CD之间有三个拐点时:∠A+∠F1 +∠C = ∠E1 +∠E2.
思考:你发现了什么?
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,AB∥CD,则∠A,∠F1 ,∠F2 ,… , ∠Fn-1与∠E1 ,E2 ,…,∠Em-1,∠D之间的关系:
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
∠A+∠F1 + ∠F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+ ∠Em-1+ ∠D
新知讲解
知识点 2
添加辅助线的证明题
6. 如图,AB//CD,试说明∠B+∠D +∠DEB=360°.
F
C
A
B
D
E
解:过点 E 作 EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,∴EF//CD.
∴∠D +∠DEF=180°,
∴∠B+∠D+∠DEB=∠B+∠D+∠BEF+∠DEF =360°,即∠B+∠D+∠DEB=360°.
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,AB∥CD,则:
性质1:当有一个拐点时: ∠A+∠E+∠C= 360°.
性质2:当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°.
性质3:当有三个拐点时:∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°.
思考:你发现了什么?
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,当有 n 个拐点时 :
…
A
B
C
D
E1
E2
En
∠A+∠ E1 + ∠ E2 +…+∠ En +∠C =(n+1)×180°.
新知讲解
知识点 2
添加辅助线的证明题
7. 如图,AB//CD,探究下面图中∠P 与∠A,∠C之间的关系.
解:∠APC+∠A=∠C.理由如下:
过点 P 作 PE//AB,则∠EPA+∠A=180°.
∵ ∠EPA=∠APC+∠1,
∴ ∠APC+∠1+∠A=180°,
∴ ∠APC+∠A=180°-∠1.
∵ AB//CD,∴ PE//CD,
∴ ∠1+∠C=180°,∴ ∠C= 180°-∠1.
∴ ∠APC+∠A=∠C.
E
1
(4)
新知讲解
知识点 2
添加辅助线的证明题
7. 如图,AB//CD,探究下面图中∠P 与∠A,∠C之间的关系.
解:∠A=∠APC+∠C.理由如下:
过点 P 作 PE//AB,则∠1+∠A=180°.
∵ AB//CD,∴ PE//CD,
∴ ∠EPC+∠C=180°,即∠1+∠APC+∠C=180°,
∴ 180°-∠A+∠APC+∠C=180°.
∴ ∠A=∠APC+ ∠C.
E
1
新知讲解
知识点 2
添加辅助线的证明题
8. [2021·泉州] 问题情境:我市某中学班级数学活动小组遇到问题:如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC 的度数.经过讨论形成的思路是:如图2,过P 作 PE//AB, 通过平行线性质,可求得∠APC的度数.
图1
图2
(1)按该数学活动小组的思路,请你帮忙求出∠APC的度数;
(2)如图3,AD//BC,点P在A、B两点之间运动时,∠ADP=α,∠BCP=β. 请你判断∠CPD 、α 、β 之间有何数量关系 并说明理由;
新知讲解
知识点 2
添加辅助线的证明题
解(1)(2)小问:
解 : ( 1 ) 过 点P 作PE//AB,
∵AB//CD,∴PE//AB//CD.
∴∠A+∠APE=180°,∠C+∠CPE=180°
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,∴∠APC=∠APE+∠CPE=110°.
(2)∠CPD=α+β,理由如下:过P作PE//AD交CD于E.
∵AD//BC,∴AD//PE//BC,
∴∠DPE=α,∠CPE=β,
∴∠CPD=∠DPE+∠CPE=α+β.
新知讲解
知识点 2
添加辅助线的证明题
9. 如图 5,已知 AB∥CD,∠ABE 的平分线与
∠CDE的平分线相交于点F.
(1)在图5中,求证:
①∠ABE + ∠CDE + ∠E = 360°;
②∠ABF + ∠CDF = ∠BFD;
图5
图6
新知讲解
知识点 2
添加辅助线的证明题
解(1)小问:
①如图,过点E作EN//AB,∵EN//AB,根据两直线平行,同旁内角互补,得 ∠ABE+∠BEN=180°,∵AB//CD,AB//NE,根据平行于同一条直线的两条直线,也互相平行,得NE//CD,根据两直线平行,同旁内角互补,得∠CDE+∠NED=180°,根据等式的性质,得∠ABE+∠E+∠CDE=36O°;
②如图,过点F作FG//AB,∵FG//AB,根据两直线平行,内错角相等,得∠ABF=∠BFG,∵AB//CD,FG//AB,根据平行于同一条直线的两条直线,也互相平行,得FG//CD,根据两直线平行,内错角相等,得∠CDF=∠GFD,根据等式的性质得∠ABF+∠CDF=∠BFG+∠GFD=∠BFD;
新知讲解
知识点 2
添加辅助线的证明题
解(2)小问:
结论:∠E+∠M=360°.∵设∠ABM=x,∠CDM=Y,则∠FBM=2x,∠EBF=3x,∠FDM=2y,∠EDF=3y,由(1)得∠ABE+∠E+∠CDE=360°,∴6x+6Y+∠E=360°,∴∠M+∠EBM+∠E+∠EDM=360°,∴6x+6y+∠E=∠M+5x+5y+∠E,∴∠M=x+y,∴∠E+6∠M=360°;
图6
新知讲解
知识点 3
运用平行线解决实际问题
平行线在实际生活中随处可见.
如图 8,在平面内每一点的南北方向互相平行,每一点的东西方向也互相平行;
如图 9,一条公路经过两次拐弯后要和原来的方向相同,必须保证所形成的同旁内角互补;
如图10,纸的两边无论如何折叠都互相平行.
新知讲解
知识点 3
运用平行线解决实际问题
10. 如图,MN,EF 表示两面互相平行的镜面,光线 AB 照射到镜面 MN 上,反射光线为 BC,此时∠1=∠2;光线 BC 经过镜面 EF 反射后的光线为 CD,此时∠3=∠4.试判断 AB 与 CD 的位置关系,并说明理由.
新知讲解
知识点 3
运用平行线解决实际问题
解:AB//CD.理由如下:
∵ MN//EF(已知),
∴ ∠2=∠3(两直线平行,内错角相等).
∵ ∠1=∠2,∠3=∠4(已知),
∴ ∠1=∠2=∠3=∠4, ∴∠1+∠2=∠3+∠4.
∵ ∠ABC+∠1+∠2=180°,
∠BCD+∠3+∠4=180°(平角的性质),
∴ ∠ABC=∠BCD(等量代换).
∴ AB//CD(内错角相等,两直线平行).
课后总结
课后总结
判定:已知角的关系得平行的关系.
推平行,用判定.
性质:已知平行的关系得角的关系.
知平行,用性质.
平行线的“判定”与“性质”有什么不同:
课后总结
典例精析
考点1:平行线性质和判定的综合应用
A.36° B.46° C.126° D.136°
1. [2021·陕西] 如图,直线l1∥l2,直线l1、l2被直线l3所截,若∠1=54°,则∠2的大小为( )
解:∵l1∥l2,
∴∠1=∠3=54°.
∴∠2=180°-∠3=180°-54°=126°.故选C.
C
3
课后总结
典例精析
考点2:添加辅助线的证明题
2. [2022·深圳] 如图,若AB∥CD,则α、β、γ满足的关系式为( )
A.α+β+γ=360° B.α-β+γ=180°
C.α+β-γ=180° D.α+β+γ=180°
解:如图,过点E作EF∥AB.易得AB∥CD∥EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∵∠AEC=β,∴∠FEA=β-γ,∴α+(β-γ)=180°即α+β-γ=180°.故选C.
C
课后总结
典例精析
考点3:运用平行线解决实际问题
3. [2020·山东] 一副直角三角板按如图所示的方式放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15°
C.18° D.30°
解:由题意可得∠EDF=45°,∠ABC=30°,
∵AB∥CF,∴∠ABD=∠EDF=45°,
∴∠DBC=∠ABD-∠ABC=45°-30°=15°.故选B.
B
A.112° B.110° C.108° D.106°
课后总结
典例精析
考点3:运用平行线解决实际问题
4. [2019·浙江] 如图,将长方形ABCD沿GH所在直线折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
D
拓展延伸
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
5. [2022·广东] 如图,点B、C在线段AD的异侧,点E、F分别在线段AB、CD上,∠AEG=∠AGE,,∠C=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,求证:∠B=∠C;
(3)在(2)的条件下,若∠BFC=4∠C,求∠D的度数.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
解:(1)证明:∵∠AEG=∠AGE,∠C=∠DGC,∠AGE=∠DGC,∴∠AEG=∠C,
∴AB∥CD.
(2)证明:∵∠AGE=∠DGC,∠AGE+∠AHF=180°,∴∠DGC+∠AHF=180°,
∴EC∥BF,∴∠B=∠AEG,由(1)得∠AEG=∠C.∴∠B=∠C.
(3)由(2)得EC∥BF,
∴∠BFC+∠C=180°,∵∠BFC=4∠C,∴∠C=36°,∴∠DGC=36°.
∵∠C+∠DGC+∠D=180°,∴∠D=108°.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
6. 将一副三角板的直角重合放置,如图1所示,
(1)图1中∠BEC的度数为______;
(2)三角板△AOB的位置保持不动,将三角板△COD绕其直角顶点O顺时针方向旋转:①当旋转至图2所示位置时,恰好OD∥AB,求此时∠AOC的大小;②若将三角板△COD继续绕O旋转,直至回到图1位置,在这一过程中,是否会存在△COD其中一边能与AB平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
解:(1)∠CAE=180°﹣∠BAO=180°﹣60°=120°,
∴∠BEC=∠C+∠CAE=45°+120°=165°,
故答案为:165°.
(2)①∵OD∥AB,∴∠BOD=∠B=30°,又∠BOD+∠BOC=90°,∠AOC+∠BOC=90°,∴∠AOC=∠BOD=30°.
②存在。
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
如图1,∠AOC=120°;如图2,∠AOC=165°;如图3,∠AOC=45°;如图4,∠AOC=150°;如图5,∠AOC=60°;如图6,∠AOC=15°.
新知讲解
这类题目要注意:
首先:要回答题目的问题,不能直接写证明过程;
注意:充分运用三角板角度的数量特性,确定动态下图形构成可能出现三线八角模型,并注意性质和判定是综合起来进行运用。
解题秘籍
考点1: 进阶 · 平行线性质和判定的综合应用
7. 如图1是一个舞台,上下两边a、b平行.在A、B两点处各有一个旋转灯,其灯光为一条射线,开始表演前,两灯均指向正右方.开始表演的瞬间,A灯开始顺时针旋转,速度为4°/分钟,B灯开始逆时针旋转,速度为5°/分钟,A灯转半圈停止,B灯转一圈停止.
(1)开始表演后t分钟,两灯灯光所在直线平行,求t.
(2)当B灯在旋转过程中某一时刻正好照向A点,A灯灯光与B灯灯光正好垂直,若此时A灯灯光照向直线b上的M点,求∠AMB的度数.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
动图演绎↓
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
解:(1)∠EAC=4t,∠DBF=5t
① 4t+5t=180,t=20,如图3,
② 4t=360-5t,t=40,如图4,
(2)5t+4t=90, t=10,∠AMB=4t=40°,如图5。
图3
图4
图5
7.2.3 平行线的性质
第二课时
第7章 相交线与平行线
人教版(新教材)数学七年级下册
《目录》
3
课后总结
4
拓展延伸
1
新课导入
2
新知讲解
学习目标
1.掌握平行线的性质与判定的区别与联系,发展推理意识,能够理解数学基本概念之间的联系.
2.会能综合运用平行线的性质与判定进行推理和计算,锻炼识图能力,会对已有条件进行归纳与转化,提升应用能力.
3.通过对平行线的性质与判定的运用,培养数学语言表达能力,发展应用意识和决策能力.
新课导入
新课导入
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
思考:平行线的判定与性质之间有什么关系?
新课导入
性质 文字语言 符号语言 图示
性质1 两直线平行,同位角相等 如果 a//b, 那么∠1=∠2
性质2 两直线平行,内错角相等 如果 a//b, 那么∠2=∠3 性质3 两直线平行,同旁内角互补 如果 a//b, 那么∠2+∠4=180° 思考:上节课我们学行线的哪些性质?
新知讲解
新知讲解
知识点 1
平行线性质和判定的综合应用
解:(1) DE∥BC. 理由如下:
∵ ∠ADE=60°,∠B = 60°,
∴ ∠ADE=∠B.
∴ DE∥BC. (同位角相等,两直线平行)
1. 如图,在三角形 ABC 中,D 是 AB 上一点,E 是 AC 上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(1) DE 和 BC 平行吗?为什么?
新知讲解
知识点 1
平行线性质和判定的综合应用
1. 如图,在三角形 ABC 中,D 是 AB 上一点,E 是 AC 上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(2)∠C 是多少度?为什么?
解:(2) ∠C =40°. 理由如下:
由(1)得 DE∥BC,
∴ ∠C=∠AED. (两直线平行,同位角相等)
又∵∠AED=40°,
∴ ∠C=∠AED =40°.
新知讲解
知识点 1
平行线性质和判定的综合应用
2. 如图,AB∥CD,如果∠1 = ∠2,那么 EF 与 AB
平行吗?说说你的理由.
解:平行,理由:因为∠1 =∠2,
根据“内错角相等,两直线平行”,
所以 EF∥CD.
又因为 AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以 EF∥AB.
新知讲解
知识点 1
平行线性质和判定的综合应用
3. 如图,已知直线 a∥b,直线 c∥d,∠1 = 107°,求∠2,∠3 的度数.
解:因为 a∥b,
所以 ∠1+∠3 = 180°,所以∠3 = 73°.
根据“两直线平行,内错角相等”,
所以 ∠2 =∠1 = 107°.
因为 c∥d,
根据“两直线平行,同旁内角互补”,
新知讲解
知识点 1
平行线性质和判定的综合应用
4. 如图 1,DB∥FG∥EC,∠ABD = 60°,∠ACE = 40°,AP 平分∠BAC.(1)求∠BAG的度数.(2)求∠PAG的度数.
新知讲解
知识点 2
添加辅助线的证明题
B
D
C
E
A
解:如图,过点 E 作 EF//AB.
∴∠B=∠BEF.
∵AB//CD,∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF =∠DEB,
即∠B+∠D=∠DEB.
F
5. 如图,若 AB//CD,你能确定∠B、∠D 与∠BED 之间的关系吗?说说你的看法.
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,AB∥CD,则:
性质1:当AB与CD之间有一个拐点时:∠A+∠C= ∠E.
性质2:当AB与CD之间有两个拐点时:∠A+∠F= ∠E +∠D.
性质3:当AB与CD之间有三个拐点时:∠A+∠F1 +∠C = ∠E1 +∠E2.
思考:你发现了什么?
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,AB∥CD,则∠A,∠F1 ,∠F2 ,… , ∠Fn-1与∠E1 ,E2 ,…,∠Em-1,∠D之间的关系:
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
∠A+∠F1 + ∠F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+ ∠Em-1+ ∠D
新知讲解
知识点 2
添加辅助线的证明题
6. 如图,AB//CD,试说明∠B+∠D +∠DEB=360°.
F
C
A
B
D
E
解:过点 E 作 EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,∴EF//CD.
∴∠D +∠DEF=180°,
∴∠B+∠D+∠DEB=∠B+∠D+∠BEF+∠DEF =360°,即∠B+∠D+∠DEB=360°.
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,AB∥CD,则:
性质1:当有一个拐点时: ∠A+∠E+∠C= 360°.
性质2:当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°.
性质3:当有三个拐点时:∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°.
思考:你发现了什么?
新知讲解
知识点 2
添加辅助线的证明题
一般地,如图,当有 n 个拐点时 :
…
A
B
C
D
E1
E2
En
∠A+∠ E1 + ∠ E2 +…+∠ En +∠C =(n+1)×180°.
新知讲解
知识点 2
添加辅助线的证明题
7. 如图,AB//CD,探究下面图中∠P 与∠A,∠C之间的关系.
解:∠APC+∠A=∠C.理由如下:
过点 P 作 PE//AB,则∠EPA+∠A=180°.
∵ ∠EPA=∠APC+∠1,
∴ ∠APC+∠1+∠A=180°,
∴ ∠APC+∠A=180°-∠1.
∵ AB//CD,∴ PE//CD,
∴ ∠1+∠C=180°,∴ ∠C= 180°-∠1.
∴ ∠APC+∠A=∠C.
E
1
(4)
新知讲解
知识点 2
添加辅助线的证明题
7. 如图,AB//CD,探究下面图中∠P 与∠A,∠C之间的关系.
解:∠A=∠APC+∠C.理由如下:
过点 P 作 PE//AB,则∠1+∠A=180°.
∵ AB//CD,∴ PE//CD,
∴ ∠EPC+∠C=180°,即∠1+∠APC+∠C=180°,
∴ 180°-∠A+∠APC+∠C=180°.
∴ ∠A=∠APC+ ∠C.
E
1
新知讲解
知识点 2
添加辅助线的证明题
8. [2021·泉州] 问题情境:我市某中学班级数学活动小组遇到问题:如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC 的度数.经过讨论形成的思路是:如图2,过P 作 PE//AB, 通过平行线性质,可求得∠APC的度数.
图1
图2
(1)按该数学活动小组的思路,请你帮忙求出∠APC的度数;
(2)如图3,AD//BC,点P在A、B两点之间运动时,∠ADP=α,∠BCP=β. 请你判断∠CPD 、α 、β 之间有何数量关系 并说明理由;
新知讲解
知识点 2
添加辅助线的证明题
解(1)(2)小问:
解 : ( 1 ) 过 点P 作PE//AB,
∵AB//CD,∴PE//AB//CD.
∴∠A+∠APE=180°,∠C+∠CPE=180°
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,∴∠APC=∠APE+∠CPE=110°.
(2)∠CPD=α+β,理由如下:过P作PE//AD交CD于E.
∵AD//BC,∴AD//PE//BC,
∴∠DPE=α,∠CPE=β,
∴∠CPD=∠DPE+∠CPE=α+β.
新知讲解
知识点 2
添加辅助线的证明题
9. 如图 5,已知 AB∥CD,∠ABE 的平分线与
∠CDE的平分线相交于点F.
(1)在图5中,求证:
①∠ABE + ∠CDE + ∠E = 360°;
②∠ABF + ∠CDF = ∠BFD;
图5
图6
新知讲解
知识点 2
添加辅助线的证明题
解(1)小问:
①如图,过点E作EN//AB,∵EN//AB,根据两直线平行,同旁内角互补,得 ∠ABE+∠BEN=180°,∵AB//CD,AB//NE,根据平行于同一条直线的两条直线,也互相平行,得NE//CD,根据两直线平行,同旁内角互补,得∠CDE+∠NED=180°,根据等式的性质,得∠ABE+∠E+∠CDE=36O°;
②如图,过点F作FG//AB,∵FG//AB,根据两直线平行,内错角相等,得∠ABF=∠BFG,∵AB//CD,FG//AB,根据平行于同一条直线的两条直线,也互相平行,得FG//CD,根据两直线平行,内错角相等,得∠CDF=∠GFD,根据等式的性质得∠ABF+∠CDF=∠BFG+∠GFD=∠BFD;
新知讲解
知识点 2
添加辅助线的证明题
解(2)小问:
结论:∠E+∠M=360°.∵设∠ABM=x,∠CDM=Y,则∠FBM=2x,∠EBF=3x,∠FDM=2y,∠EDF=3y,由(1)得∠ABE+∠E+∠CDE=360°,∴6x+6Y+∠E=360°,∴∠M+∠EBM+∠E+∠EDM=360°,∴6x+6y+∠E=∠M+5x+5y+∠E,∴∠M=x+y,∴∠E+6∠M=360°;
图6
新知讲解
知识点 3
运用平行线解决实际问题
平行线在实际生活中随处可见.
如图 8,在平面内每一点的南北方向互相平行,每一点的东西方向也互相平行;
如图 9,一条公路经过两次拐弯后要和原来的方向相同,必须保证所形成的同旁内角互补;
如图10,纸的两边无论如何折叠都互相平行.
新知讲解
知识点 3
运用平行线解决实际问题
10. 如图,MN,EF 表示两面互相平行的镜面,光线 AB 照射到镜面 MN 上,反射光线为 BC,此时∠1=∠2;光线 BC 经过镜面 EF 反射后的光线为 CD,此时∠3=∠4.试判断 AB 与 CD 的位置关系,并说明理由.
新知讲解
知识点 3
运用平行线解决实际问题
解:AB//CD.理由如下:
∵ MN//EF(已知),
∴ ∠2=∠3(两直线平行,内错角相等).
∵ ∠1=∠2,∠3=∠4(已知),
∴ ∠1=∠2=∠3=∠4, ∴∠1+∠2=∠3+∠4.
∵ ∠ABC+∠1+∠2=180°,
∠BCD+∠3+∠4=180°(平角的性质),
∴ ∠ABC=∠BCD(等量代换).
∴ AB//CD(内错角相等,两直线平行).
课后总结
课后总结
判定:已知角的关系得平行的关系.
推平行,用判定.
性质:已知平行的关系得角的关系.
知平行,用性质.
平行线的“判定”与“性质”有什么不同:
课后总结
典例精析
考点1:平行线性质和判定的综合应用
A.36° B.46° C.126° D.136°
1. [2021·陕西] 如图,直线l1∥l2,直线l1、l2被直线l3所截,若∠1=54°,则∠2的大小为( )
解:∵l1∥l2,
∴∠1=∠3=54°.
∴∠2=180°-∠3=180°-54°=126°.故选C.
C
3
课后总结
典例精析
考点2:添加辅助线的证明题
2. [2022·深圳] 如图,若AB∥CD,则α、β、γ满足的关系式为( )
A.α+β+γ=360° B.α-β+γ=180°
C.α+β-γ=180° D.α+β+γ=180°
解:如图,过点E作EF∥AB.易得AB∥CD∥EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∵∠AEC=β,∴∠FEA=β-γ,∴α+(β-γ)=180°即α+β-γ=180°.故选C.
C
课后总结
典例精析
考点3:运用平行线解决实际问题
3. [2020·山东] 一副直角三角板按如图所示的方式放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15°
C.18° D.30°
解:由题意可得∠EDF=45°,∠ABC=30°,
∵AB∥CF,∴∠ABD=∠EDF=45°,
∴∠DBC=∠ABD-∠ABC=45°-30°=15°.故选B.
B
A.112° B.110° C.108° D.106°
课后总结
典例精析
考点3:运用平行线解决实际问题
4. [2019·浙江] 如图,将长方形ABCD沿GH所在直线折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
D
拓展延伸
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
5. [2022·广东] 如图,点B、C在线段AD的异侧,点E、F分别在线段AB、CD上,∠AEG=∠AGE,,∠C=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,求证:∠B=∠C;
(3)在(2)的条件下,若∠BFC=4∠C,求∠D的度数.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
解:(1)证明:∵∠AEG=∠AGE,∠C=∠DGC,∠AGE=∠DGC,∴∠AEG=∠C,
∴AB∥CD.
(2)证明:∵∠AGE=∠DGC,∠AGE+∠AHF=180°,∴∠DGC+∠AHF=180°,
∴EC∥BF,∴∠B=∠AEG,由(1)得∠AEG=∠C.∴∠B=∠C.
(3)由(2)得EC∥BF,
∴∠BFC+∠C=180°,∵∠BFC=4∠C,∴∠C=36°,∴∠DGC=36°.
∵∠C+∠DGC+∠D=180°,∴∠D=108°.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
6. 将一副三角板的直角重合放置,如图1所示,
(1)图1中∠BEC的度数为______;
(2)三角板△AOB的位置保持不动,将三角板△COD绕其直角顶点O顺时针方向旋转:①当旋转至图2所示位置时,恰好OD∥AB,求此时∠AOC的大小;②若将三角板△COD继续绕O旋转,直至回到图1位置,在这一过程中,是否会存在△COD其中一边能与AB平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
解:(1)∠CAE=180°﹣∠BAO=180°﹣60°=120°,
∴∠BEC=∠C+∠CAE=45°+120°=165°,
故答案为:165°.
(2)①∵OD∥AB,∴∠BOD=∠B=30°,又∠BOD+∠BOC=90°,∠AOC+∠BOC=90°,∴∠AOC=∠BOD=30°.
②存在。
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
如图1,∠AOC=120°;如图2,∠AOC=165°;如图3,∠AOC=45°;如图4,∠AOC=150°;如图5,∠AOC=60°;如图6,∠AOC=15°.
新知讲解
这类题目要注意:
首先:要回答题目的问题,不能直接写证明过程;
注意:充分运用三角板角度的数量特性,确定动态下图形构成可能出现三线八角模型,并注意性质和判定是综合起来进行运用。
解题秘籍
考点1: 进阶 · 平行线性质和判定的综合应用
7. 如图1是一个舞台,上下两边a、b平行.在A、B两点处各有一个旋转灯,其灯光为一条射线,开始表演前,两灯均指向正右方.开始表演的瞬间,A灯开始顺时针旋转,速度为4°/分钟,B灯开始逆时针旋转,速度为5°/分钟,A灯转半圈停止,B灯转一圈停止.
(1)开始表演后t分钟,两灯灯光所在直线平行,求t.
(2)当B灯在旋转过程中某一时刻正好照向A点,A灯灯光与B灯灯光正好垂直,若此时A灯灯光照向直线b上的M点,求∠AMB的度数.
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
动图演绎↓
拓展延伸
典例精析
考点1: 进阶 · 平行线性质和判定的综合应用
解:(1)∠EAC=4t,∠DBF=5t
① 4t+5t=180,t=20,如图3,
② 4t=360-5t,t=40,如图4,
(2)5t+4t=90, t=10,∠AMB=4t=40°,如图5。
图3
图4
图5
同课章节目录
