人教版五年级数学上册《解决问题》期末复习练习题(含解析)
文档属性
| 名称 | 人教版五年级数学上册《解决问题》期末复习练习题(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 503.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版五年级数学上册《解决问题》期末复习练习题(含答案)
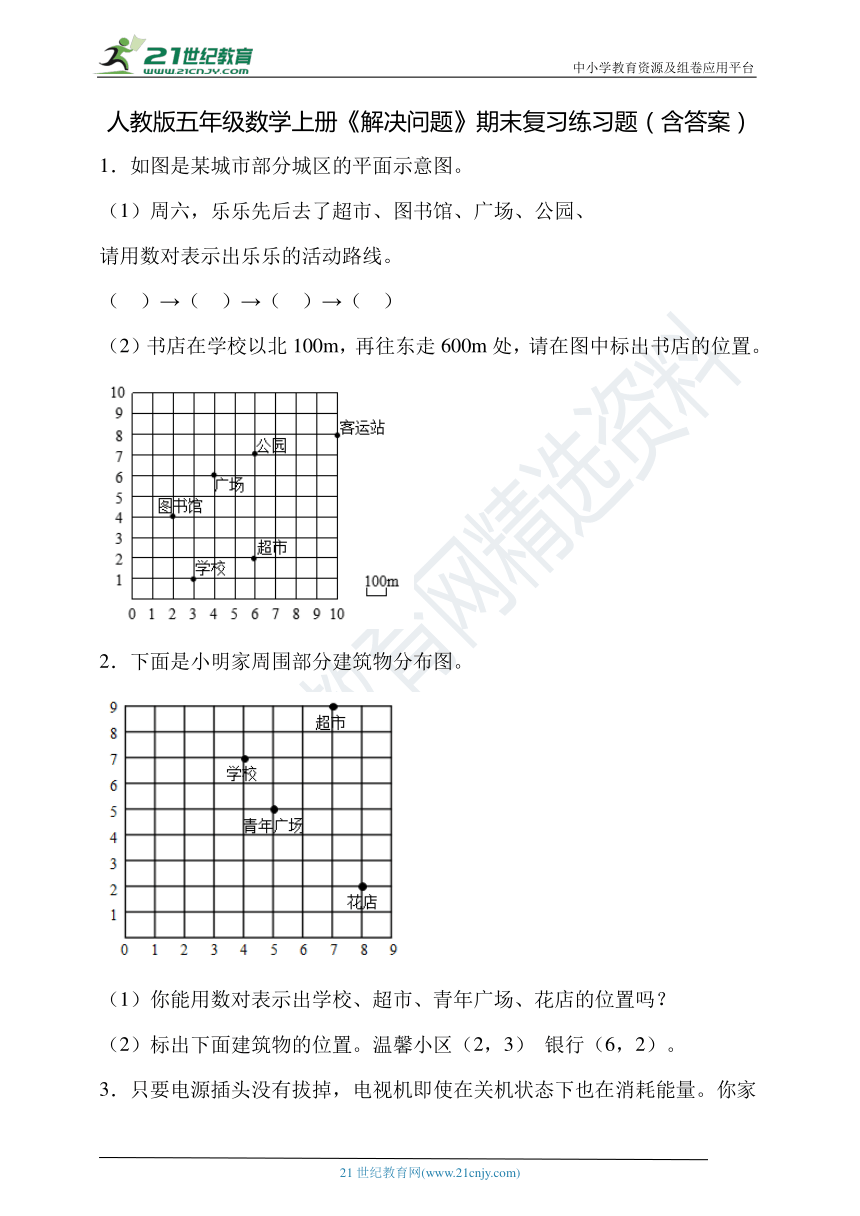
1.如图是某城市部分城区的平面示意图。
(1)周六,乐乐先后去了超市、图书馆、广场、公园、
请用数对表示出乐乐的活动路线。
( )→( )→( )→( )
(2)书店在学校以北100m,再往东走600m处,请在图中标出书店的位置。
2.下面是小明家周围部分建筑物分布图。
(1)你能用数对表示出学校、超市、青年广场、花店的位置吗?
(2)标出下面建筑物的位置。温馨小区(2,3) 银行(6,2)。
3.只要电源插头没有拔掉,电视机即使在关机状态下也在消耗能量。你家一台电视机一年(按365天计算)在这一项上要耗电多少千瓦时?
4.某快递公司收费标准如下:5千克及5千克以下每个包裹收费20元,超过5千克的每超过1千克加收5元(不足1千克的按1千克计算)。李阿姨寄了一个8.2千克的包裹,应付快递费多少元?
5.小明妈妈去水果市场买水果,她先花10元买了2.5千克的橘子,还要买5千克的苹果,苹果的单价是橘子的1.6倍,她买苹果一共付了多少元
6.李阿姨买了一套新房子,房子的建筑面积是68.2平方米,按照合同李阿姨要交一年的垃圾处理费102.3元。小区的垃圾处理费每年每平方米多少钱?
7.某家快递公司在双十一期间的运费标准如下:1千克以内10元,超出部分2.5元/千克(不足1千克按1千克计算)
(1)如果邮寄13.8千克的物品,需要支付运费多少钱?
(2)店家邮寄一些物品,一共付费25元,这些物品最多重多少千克?
8.育新小学400学生和36名老师去参加活动,每辆车限乘45人,租10辆车够吗?
9.顺达运输队要运8.4万块砖,每小时运3.5万块,正好按时运完,如果要提前0.4小时运完,每小时需要运多少万块?
10.李叔叔住在12层,有一次电梯坏了,他从下面上到4层用了60秒。照这样的速度,他步行还要走多少秒才能走到12层?
11.如图:平行四边形的面积是240cm2,求阴影部分的面积.
12.一本书有a页,妙妙已经看了b天,每天看25页。
(1)用含有字母的式子表示还剩下多少页没有看。
(2)当a=243,b=7时,还剩多少页没有看?
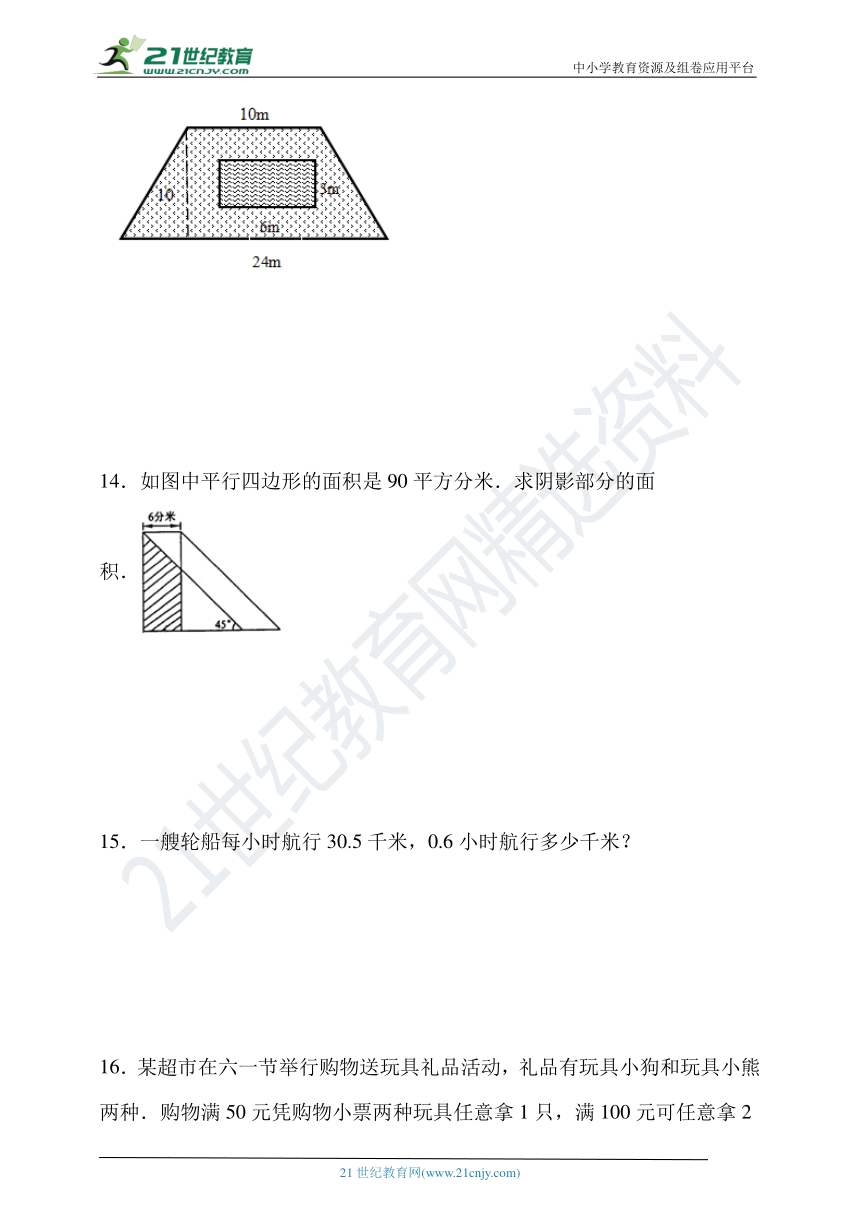
13.一块梯形的草坪,中间有一个水池,如下图。①求图中草坪的面积是多少平方米?②如果每平方米种植12棵草,每棵草5元钱,这块草坪需要多少元?
14.如图中平行四边形的面积是90平方分米.求阴影部分的面积.
15.一艘轮船每小时航行30.5千米,0.6小时航行多少千米?
16.某超市在六一节举行购物送玩具礼品活动,礼品有玩具小狗和玩具小熊两种.购物满50元凭购物小票两种玩具任意拿1只,满100元可任意拿2只.洋洋与妈妈购物达到110元,洋洋可能怎么拿?请你把每一种可能列举出来.
17.为了促进同学们的健康成长,激发运动兴趣,形成健康意识和终身体育观,确保“健康第一”,阳光小学六(2)班为“阳光大课间”活动,购买了40个毽子和36根跳绳。每个毽子的价钱是5.5元,每根跳绳的价钱是每个毽子的1.4倍。一共花了多少钱?
18.一辆汽车从甲地开往乙地,平均每小时行驶62千米,4.5小时到达。如果每小时行驶75千米,3.5小时能到达吗?
19.某城市出租车的收费标准是:3千米以内收费8元,3千米以外每千米收费1.8元(不足1千米按1千米计算),双休日小明从家打车去图书馆,共付了11.6元,他家到图书馆最远是多少千米?
20.淘气家上半年用水量76.2吨,每吨水的价格是2.7元,平均每个月需要付多少元水费?
21.文具店的英语本和数学本的价格相同,王芳买了5本英语本和4本数学本,每本1.8元。她带了10元钱,够用吗?(填够用或不够用)
22.一块梯形草地面积是450m2,梯形的下底是30m,上底的长度是下底的一半,这块梯形草地的高是多少米?
23.一块长方形广告牌长9.2米、宽5米,用油漆刷这块广告牌的一面,每平方米用油漆0.76千克,已知每桶油漆净重15千克。
(1)刷这块广告牌要用油漆多少千克?
(2)至少需要买回多少桶油漆?
24.三角形ABC三个顶点的位置用数对表示分别为A(2,1)、B(6,1)、C(4,7)。
(1)请将三角形ABC画在方格图中。
(2)三角形ABC的面积是( )cm2。(每个小方格的边长是1cm)
(3)以AB为底,画出一个与这个三角形面积相等的平行四边形。
25.科技书有55本,比故事书的3倍少14本。故事书有多少本?(用方程解答)
26.一套桌椅的售价是280元,已知桌子的单价是椅子的3倍,桌子和椅子的单价分别是多少元?
27.一块平行四边形的牌匾,底是20.2米,高是4.2米,给这块牌匾刷上油漆,每平方米用油漆0.6千克,需要多少千克油漆?
28.甲乙两车从A、B两地同时相向开出,甲车每小时行54千米,乙车每小时行60千米。两车相遇时,乙车比甲车多行了18千米,A、B两地相距多少千米?
29.如图是一块梯形菜地的示意图,张大伯把它分成一个平行四边形和一个三角形.平行四边形地里种大白菜,三角形地里种萝卜.
(1)每棵大白菜占地0.16m ,一共可以种多少棵?
(2)萝卜地一共有多少平方米?
30.葡萄每千克4.5元,苹果每千克4.1元,小丽付20元够吗?
31.为鼓励居民节约用电,重庆市电力公司制订下列收费办法:每户每月用电100度以内(含100度),1.8元/度。超出100度部分,按2.5元/度收取。
(1)小明家九月份用电120度,该交电费多少元?
(2)小红家十月份交电费225元,她家十月份用电多少度?
32.3台洒水车,0.4小时可以喷洒地面3.6公顷。照这样计算,一台洒水车1小时可喷洒多少公顷?
33.有两桶油,甲桶油的质量是乙桶油的1.8倍,如果从甲桶中取出1.2千克油倒入乙桶油中,两桶油的质量就相等了。原来两桶中各有油多少千克?(列方程解答)
34.沙茶面是福建省厦门市的一道传统小吃,某餐饮店在假期推出了以下三种套餐。
A套餐 B套餐 C套餐
16.5元/份 24.8元/份 20.6元/份
某旅游团在该店吃沙茶面,用500元买了16份A套餐,剩下的钱最多还能买多少份B套餐?
35.小明妈妈带了100元钱,打算买13千克苹果和9千克桃子,钱够吗?
36.下面每个小方格的边长都表示1厘米,请你按要求画图。
(1)画出一个面积是15平方厘米的平行四边形。
(2)画一个面积是12平方厘米、高是3厘米的梯形。
(3)用数对表示平行四边形各个顶点的位置。
37.张叔叔选择的上网收费标准是:每月缴费30元可以上网50小时,超过50小时每小时收费1.2元。张叔叔12月份上网90小时,需要缴纳多少元上网费?
38.一个梯形草地中间有一块三角形空地,其它地方都植有小草(如右图,单位:m)。植草部分的面积是多少平方米
39.学学和乐乐两人比赛射箭,每一局,胜利的一方得5分,输掉的一方减2分,平局则两人各得3分。比赛10局后,两人的分数之和为48分。那么,比赛中有多少局胜负局?
40.乐乐今年8岁,妈妈今年36岁。乐乐多少岁时,妈妈的年龄是乐乐年龄的3倍?(用方程解答)
参考答案:
1.(1)(6,2);(2,4);(4,6);(6,7)
(2)见详解
【分析】(1)根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数在前,行数在后。据此解答;
(2)根据利用方向和距离表示确定物体位置的方法,先确定方向,再确定距离。据此解答。
【详解】(1)超市的位置用数对表示是(6,2),图书馆的位置用数对表示是(2,4),广场的位置用数对表示是(4,6),公园的位置用数对表示是(6,7)。
(2)小正方形的边长是100米,书店在学校以北100m,再往东走600m处,由此可知,书店的位置用数对表示是(9,2)。
作图如下:
【点睛】此题考查的目的是理解掌握利用数对表示物体位置的方法,利用方向和距离确定物体位置的方法及应用。
2.(1)学校(4,7),超市(7,9),青年广场(5,5),花店(8,2)
(2)见详解
【分析】(1)根据用数对表示位置的方法,结合学校、超市、青年广场、花店分别所在的行数和列数,解题即可;
(2)根据温馨小区和银行的数对位置,在图上找出对应点即可。
【详解】(1)学校(4,7),超市(7,9),青年广场(5,5),花店(8,2)
(2)
【点睛】本题考查了用数对表示位置,属于基础题,解题时细心即可。
3.35.04千瓦时
【分析】用12×0.008先求出1天的耗电量,再乘365即可求出电视机一年的耗电量。
【详解】12×0.008×365
=0.096×365
=35.04(千瓦时)
答:一台电视机一年(按365天计算)在这一项上要耗电35.04千瓦时。
【点睛】本题主要考查小数连乘的简单应用。
4.40元
【分析】由题意可知,不足1千克的按1千克计算,所以8.2千克按照9千克计算,根据单价×数量=总价,先求出超过5千克的钱数,再加上20元即可求解。
【详解】(9-5)×5+20
=4×5+20
=20+20
=40(元)
答:应付快递费40元。
【点睛】本题考查单价、数量和总价,求出超过5千克的钱数是解题的关键。
5.32元
【详解】略
6.1.5元
【分析】用垃圾处理费的总钱数除以房子的建筑面积即可。
【详解】102.3÷68.2=1.5(元)
答:小区的垃圾处理费每年每平方米1.5元。
【点睛】此题考查小数除法的计算,认真解答即可。
7.(1)42.5元
(2)7千克
【分析】(1)13.8千克≈14千克;先用14千克-1千克,求出超出1千克的部分的重量,再乘2.5,求出超出部分需要付的钱数,再加上1千克以内的10元,即可求出需要支付的钱数;
(2)用一共付的钱数-10元,求出超出1千克需要支付的钱数,再用超出部分支付的钱数÷2.5,求出超出1千克部分的重量,再加上1千克,即可求出这些物品的重量。
【详解】(1)13.8千克≈14千克
10+(14-1)×2.5
=10+13×2.5
=10+32.5
=42.5(元)
答:需要支付42.5元。
(2)(25-10)÷2.5+1
=15÷2.5+1
=6+1
=7(千克)
答:这些物品最多重7千克。
8.够
【分析】利用加法求出一共有多少人需要乘车,再将总人数除以每辆车的限乘人数,利用进一法将商保留到整数部分,求出至少需要多少辆车,从而判断10辆车是否够用。
【详解】(400+36)÷45
=436÷45
≈10(辆)
答:租10辆车够。
【点睛】本题考查了商的近似数,能根据实际情况采用进一法是解题的关键。
9.4.2万块
【分析】用8.4÷3.5求出按时运完的时间,减去0.4小时即可求出提前运完的时间,再用砖的总块数除以提前运完的时间即可求出每小时需要运多少万块。
【详解】
=8.4÷2
=4.2(万块);
答:每小时需要运4.2万块。
【点睛】先求出提前运完的时间是解答本题的关键,再用总块数除以提前运完的时间即可解答。
10.160秒
【详解】60÷(4 – 1)×(12 – 4)= 160(秒)
11.80平方厘米
【详解】试题分析:根据平行四边形的面积公式:s=ah,已知平行四边形底面积和高,首先求出平行四边形的底,进而求出阴影部分三角形的底,再根据三角形的面积公式:s=ah,把数据代入公式解答.
解:240÷8=30(厘米),
(30﹣10)×,
=20×,
=80(平方厘米),
答:阴影部分的面积是80平方厘米.
点评:此题主要考查平行四边形、三角形的面积公式的灵活运用.
12.(1)a-25b;(2)68页
【分析】(1)用书的总页数减去已经看的,将还剩下多少没看表示出来;
(2)将a和b具体的值代入(1)中的式子,求出具体还剩下多少页没有看。
【详解】(1)还剩下(a-25b)页没有看;
(2)a-25b
=243-25×7
=243-175
=68(页)
答:还剩下68页没看。
【点睛】本题考查了含有字母式子的化简和求值,有一定运算能力是解题的关键。
13.①152平方米;②9120元
【分析】①观察图形可知,草坪的面积等于梯形的面积减去中间长方形的面积,根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据进行计算即可;②根据题意可知,每平方米种植12棵草,每棵草5元钱,要求种植这块草坪需要多少元钱,我们可以用每平方米种植的草的棵数乘草坪的面积,求出一共种植的草的数量,再用每棵草的价钱乘种植的草的数量,即可解答。
【详解】①由题意得:
(10+24)×10÷2
=34×10÷2
=340÷2
=170(平方米)
6×3=18(平方米)
170-18=152(平方米)
答:草坪的面积是152平方米。
②由题意得:
12×152×5
=1824×5
=9120(元)
答:这块草坪需要9120元。
14.72平方分米
【详解】试题分析:观察图形可知:图中有平行四边形ADEF,长方形ABCF,等腰直角三角形ABD和CDG;而阴影部分是一个梯形:只要求出这个梯形的上下底CG、AB和高BC的长度即可解答问题.
解:AB的长度是:90÷6=15(分米),
则BD的长度也是15分米,
因为BC=AF=6分米,
所以CD=DG=15﹣6=9(分米),
所以阴影部分的面积是:(9+15)×6÷2,
=24×3,
=72(平方分米);
答:阴影部分的面积是72平方分米.
点评:此题要充分利用图中已知的平行四边形、长方形、等腰直角三角形的性质进行解答.
15.18.3千米
【分析】根据路程=时间×速度,列式即可。
【详解】30.5×0.6=18.3(千米)
答:0.6小时航行18.3千米。
【点睛】关键是理解速度、时间、路程之间的关系,掌握小数乘小数的计算方法。
16.①玩具小狗2只; ②玩具小狗1只,玩具小熊1只 ;③玩具小熊2只
【解析】略
17.497.2元
【分析】根据求一个数的几倍是多少,用乘法计算,用5.5乘1.4即可求出每根跳绳的钱数,再根据单价×数量=总价,据此求出40个毽子和36根跳绳的钱数,然后再相加即可。
【详解】5.5×1.4×36+5.5×40
=7.7×36+5.5×40
=277.2+220
=497.2(元)
答:一共花了497.2元。
【点睛】本题考查小数乘法,明确单价、数量和总价之间的关系是解题的关键。
18.不能
【分析】根据速度×时间=路程,用62乘4.5即可求出甲地和乙地之间的路程,再根据路程÷速度=时间,据此求出每小时行驶75千米时所用的时间,再与3.5对比即可。
【详解】62×4.5=279(千米)
279÷75=3.72(小时)
3.72>3.5
答:3.5小时不能到达。
【点睛】本题考查小数乘除法,明确路程、速度和时间之间的关系是解题的关键。
19.5千米
【分析】首先用小明从家打车去图书馆共付的钱数减去起步价,求出超过起步价的费用是多少;然后用超过起步价的费用除以3千米以外每千米的收费,求出超过3千米的路程是多少,再加上3千米,即求出他家到图书馆的最远距离。
【详解】(11.6-8)÷1.8+3
=3.6÷1.8+3
=2+3
=5(千米)
答:他家到图书馆最远是5千米。
【点睛】解答此题的关键是求出超过起步价的费用,以及超过3千米的路程是多少。
20.34.29元
【分析】根据总价=单价×数量,将数据代入,先算出淘气家上半年付的水费,再除以月数,即可得出答案。
【详解】半年有6个月。
76.2×2.7÷6
=205.74÷6
=34.29(元)
答:平均每个月需要付34.29元。
【点睛】本题考查学生对小数乘除法的掌握和运用。
21.不够
【分析】因为两种本子的价钱相同,所以先求出英语本和数学本的总本数,再乘每本的价钱,求出花费的总钱数,再与带的钱数比较大小。
【详解】(5+4)×1.8
=9×1.8
=16.2(元)
16.2>10
答:不够用。
【点睛】本题考查经济问题,先求出总数量,再根据总价、单价和数量之间的关系解答。
22.20米
【分析】根据“梯形面积=(上底+下底)×高÷2”,得“高=梯形面积×2÷(上底+下底)”,据此计算得解。
【详解】450×2÷(30+30÷2)
=900÷(30+15)
=900÷45
=20(米)
答:这块梯形草地的高是20米。
【点睛】本题考查梯形面积,关键是熟练掌握梯形面积公式,并会运用逆运算对公式进行变形,本题也可列方程求解。
23.(1)34.96千克
(2)3桶
【分析】(1)利用长方形面积公式:S=ab计算长方形广告牌的面积,再乘每平方米所需油漆的质量,求出所需油漆的质量即可;
(2)根据(1)的结果,用所需油漆的质量除以每桶油漆的质量,求油漆的桶数。商不是整数时,利用进一法保留整数。
【详解】(1)9.2×5=46(平方米)
46×0.76=34.96(千克)
答:刷这块广告牌要用油漆34.96千克。
(2)34.96÷15≈2.33≈3(桶)
答:至少需要买回3桶油漆。
24.(1)(3)图见详解
(2)12
【分析】(1)用数对表示位置时,括号里第一个数字表示列,第二个数字表示行,据此找到点的位置,再将各点一次连接成图形即可。
(2)数出三角形底和高的方格数,可以知道它们的长度,再根据三角形面积=底×高÷2,进行计算即可。
(3)平行四边形面积=底×高,底不变与它面积相等的三角形的高是平行四边形高的2倍,据此解答。
【详解】(2)4×6÷2=12(cm2)
三角形ABC的面积是12cm2。
(3)由分析得:6÷2=3(cm)
以AB为底,画出一个与这个三角形面积相等的平行四边形的高为3cm。
(1)(3)如下图:
25.23本
【分析】根据题干可得等量关系:故事书的3倍-14本=科技书的本数,据此设故事书有x本,列出方程解决问题。
【详解】解:设故事书有x本。
3x-14=55
3x=55+14
3x=69
x=23
答:故事书有23本。
【点睛】解答此题容易找出基本数量关系:故事书的3倍-14本=科技书的本数,由此列方程解决问题。
26.桌子210元;椅子70元
【分析】首先假设椅子的单价是x元,根据已知桌子的单价是椅子的3倍,所以桌子的单价就是3x元,一套桌椅的售价是280元就是一张桌子加上一把椅子的价格,也是桌子的单价加上椅子的单价,即3x加上x等于280,通过解方程求出x,求出的x就是椅子的单价,再用x的值与3相乘,就是桌子的单价。据此解答即可。
【详解】解:设椅子的单价是x元,桌子的单价是3x元。
x+3x=280
4x=280
4x÷4=280÷4
x=70
3x=3×70=210(元)
答:桌子的单价是210元,椅子的单价是70元。
27.50.904千克
【详解】20.2×4.2×0.6
=84.84×0.6
=50.904(千克)
答:需要50.904千克油漆.
28.342千米
【分析】把相遇时间设为未知数,等量关系式:乙车速度×相遇时间-甲车速度×相遇时间=乙车比甲车多行驶的路程,解方程求出相遇时间,最后根据“相遇时间×速度和=总路程”求出A、B两地之间的总路程,据此解答。
【详解】解:设经过x小时相遇。
60x-54x=18
6x=18
x=18÷6
x=3
(54+60)×3
=114×3
=342(千米)
答:A、B两地相距342千米。
【点睛】本题主要考查相遇问题,找出等量关系式并列方程求出相遇时间是解答题目的关键。
29.(1)180棵;(2)10.8平方米
【详解】(1)6.4×4.5÷0.16=180(棵)
(2)(11.2-6.4)×4.5÷2=10.8(平方米)
30.不够
【详解】4.5×3.6+4.1=20.3(元) 20.3元>20元 答:小丽付20元不够.
31.(1)230元;(2)118度
【分析】(1)由题意可知,超过100度的部分有(120-100)度,根据电费单价×用电量=总价,据此求出超过100度的部分的价钱,100度的电费是(100×1.8)元,然后把这两部分的钱数加起来即可得解;
(2)100度的电费是(100×1.8)元,等于180元,用十月份的电费减去180元即可求出超过100度部分的电费,再根据总价÷电费单价=用电量,据此求出超过100度部分的用电量,再加上100度,即可求出小红家十月份用电的度数。
【详解】(1)100×1.8+(120-100)×2.5
=180+20×2.5
=180+50
=230(元)
答:该交电费230元。
(2)(225-100×1.8)÷2.5+100
=(225-180)÷2.5+100
=45÷2.5+100
=18+100
=118(度)
答:她家十月份用电118度。
【点睛】本题考查分段计费问题,利用小数乘除法的计算法则,明确总价、用电量和单价之间的关系是解题的关键。
32.3公顷
【分析】喷洒地面面积÷时间=1小时3台洒水车喷洒面积,再除以3就是一台洒水车1小时可喷洒面积。
【详解】3.6÷0.4÷3=3(公顷)
答:一台洒水车1小时可喷洒3公顷。
【点睛】关键是掌握小数除法的计算方法。
33.甲桶有油5.4千克,乙桶有油3千克
【分析】根据题意,可知“甲桶油的质量=乙桶油的质量×1.8”“ 甲桶油的质量-1.2=乙桶油的质量+1.2”,据此列方程解答即可。
【详解】解:设乙桶有油x千克,则甲桶有油1.8x千克;
1.8x-1.2=x+1.2
0.8x=2.4
x=3;
3×1.8=5.4(千克);
答:甲桶有油5.4千克,乙桶有油3千克。
【点睛】根据甲桶和乙桶油的倍数关系设出未知量,根据变化后质量相等列方程解答。
34.9份
【分析】已知每份A套餐16.5元,买了16份,根据“总价=单价×数量”,求出买A套餐的总花费;再用总钱数减去买A套餐的总花费,就是剩下的钱数;
已知每份B套餐24.8元,求用剩下的钱数最多还能买几份B套餐,根据“数量=总价÷单价”,得数采用“去尾法”保留整数,即可求解。
【详解】A套餐共花费:16.5×16=264(元)
还剩下:500-264=236(元)
最多还能买B套餐:236÷24.8≈9(份)
答:剩下的钱最多还能买9份B套餐。
35.够
【详解】4.8×13+3.45×9
=62.4+31.05
=93.45(元)
100>93.45,够.
答:钱够.
36.(1)见详解
(2)见详解
(3)A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【分析】(1)根据平行四边形的面积计算公式找出符合条件的底和高;
(2)根据梯形的面积和高,找出出上底和下底的关系,计算符合条件的上下底;
(3)数对表示位置的方法:先写列数再写行数,中间用逗号隔开,如:(列数,行数),括号前面标注点的名称即可。
【详解】(1)平行四边形面积为15平方厘米,则底为5厘米,高为3厘米(答案不唯一)
(2)梯形的面积是12平方厘米、高是3厘米,上底+下底=12×2÷3=8(厘米),上底为2厘米,下底为6厘米(答案不唯一)
(3)平行四边形各顶点位置表示为:A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【点睛】灵活运用平行四边形和梯形的面积公式是解答题目的关键。
37.78元
【分析】张叔叔上网时间超过50小时,先求出超出50小时的小时数,超出部分×对应收费标准+50小时内的费用=需要缴纳的上网费,据此列式解答。
【详解】30+(90-50)×1.2
=30+40×1.2
=30+48
=78(元)
答:需要缴纳78元上网费。
【点睛】关键是理解收费标准,掌握小数乘法的计算方法。
38.12平方米
【详解】(6+10)×4÷2=32(平方米)
4×10÷2=20(平方米)
32-20=12(平方米)
答:植草部分的面积是12平方米。
39.4局
【分析】假设比赛中有x局胜负局,则有平局(10-x)局,每一场胜负局两人的得分之和是(5-2)分,每一场平局两人的得分之和是3×2=6分,根据数量关系:每一场胜负局两人的得分之和×胜负局的场数+每一场平局两人的得分之和×平局的场数=48,据此列出方程,求解即可。
【详解】解:设比赛中有x局胜负局,则有平局(10-x)局,
(5-2)×x+3×2×(10-x)=48
3x+6×(10-x)=48
60-3x=48
3x=60-48
3x=12
x=4
答:比赛中有4局胜负局。
【点睛】此题属于鸡兔同笼的应用题,采用列方程的方法,解题关键是弄清题意,把胜负局的场数设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
40.14岁
【分析】年龄问题中,乐乐和妈妈的年龄差一直不变,即等量关系式为: 3倍时候妈妈年龄-乐乐的年龄=今年妈妈的年龄-今年乐乐的年龄,据此列出方程即可求解。
【详解】解:设乐乐x岁时,妈妈的年龄是乐乐的3倍。
3x-x=36-8
2x=28
2x÷2=28÷2
x=14
答:当乐乐14岁时,妈妈的年龄是乐乐的3倍。
【点睛】此题考查年龄问题,抓住年龄差不变是解题的关键,举例说明:今年小明年龄10岁,妈妈今年35岁,年龄差为35-10=25岁,2年后小明12岁,妈妈37岁,年龄差还是为37-12=25岁,所以年龄差一直不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版五年级数学上册《解决问题》期末复习练习题(含答案)
1.如图是某城市部分城区的平面示意图。
(1)周六,乐乐先后去了超市、图书馆、广场、公园、
请用数对表示出乐乐的活动路线。
( )→( )→( )→( )
(2)书店在学校以北100m,再往东走600m处,请在图中标出书店的位置。
2.下面是小明家周围部分建筑物分布图。
(1)你能用数对表示出学校、超市、青年广场、花店的位置吗?
(2)标出下面建筑物的位置。温馨小区(2,3) 银行(6,2)。
3.只要电源插头没有拔掉,电视机即使在关机状态下也在消耗能量。你家一台电视机一年(按365天计算)在这一项上要耗电多少千瓦时?
4.某快递公司收费标准如下:5千克及5千克以下每个包裹收费20元,超过5千克的每超过1千克加收5元(不足1千克的按1千克计算)。李阿姨寄了一个8.2千克的包裹,应付快递费多少元?
5.小明妈妈去水果市场买水果,她先花10元买了2.5千克的橘子,还要买5千克的苹果,苹果的单价是橘子的1.6倍,她买苹果一共付了多少元
6.李阿姨买了一套新房子,房子的建筑面积是68.2平方米,按照合同李阿姨要交一年的垃圾处理费102.3元。小区的垃圾处理费每年每平方米多少钱?
7.某家快递公司在双十一期间的运费标准如下:1千克以内10元,超出部分2.5元/千克(不足1千克按1千克计算)
(1)如果邮寄13.8千克的物品,需要支付运费多少钱?
(2)店家邮寄一些物品,一共付费25元,这些物品最多重多少千克?
8.育新小学400学生和36名老师去参加活动,每辆车限乘45人,租10辆车够吗?
9.顺达运输队要运8.4万块砖,每小时运3.5万块,正好按时运完,如果要提前0.4小时运完,每小时需要运多少万块?
10.李叔叔住在12层,有一次电梯坏了,他从下面上到4层用了60秒。照这样的速度,他步行还要走多少秒才能走到12层?
11.如图:平行四边形的面积是240cm2,求阴影部分的面积.
12.一本书有a页,妙妙已经看了b天,每天看25页。
(1)用含有字母的式子表示还剩下多少页没有看。
(2)当a=243,b=7时,还剩多少页没有看?
13.一块梯形的草坪,中间有一个水池,如下图。①求图中草坪的面积是多少平方米?②如果每平方米种植12棵草,每棵草5元钱,这块草坪需要多少元?
14.如图中平行四边形的面积是90平方分米.求阴影部分的面积.
15.一艘轮船每小时航行30.5千米,0.6小时航行多少千米?
16.某超市在六一节举行购物送玩具礼品活动,礼品有玩具小狗和玩具小熊两种.购物满50元凭购物小票两种玩具任意拿1只,满100元可任意拿2只.洋洋与妈妈购物达到110元,洋洋可能怎么拿?请你把每一种可能列举出来.
17.为了促进同学们的健康成长,激发运动兴趣,形成健康意识和终身体育观,确保“健康第一”,阳光小学六(2)班为“阳光大课间”活动,购买了40个毽子和36根跳绳。每个毽子的价钱是5.5元,每根跳绳的价钱是每个毽子的1.4倍。一共花了多少钱?
18.一辆汽车从甲地开往乙地,平均每小时行驶62千米,4.5小时到达。如果每小时行驶75千米,3.5小时能到达吗?
19.某城市出租车的收费标准是:3千米以内收费8元,3千米以外每千米收费1.8元(不足1千米按1千米计算),双休日小明从家打车去图书馆,共付了11.6元,他家到图书馆最远是多少千米?
20.淘气家上半年用水量76.2吨,每吨水的价格是2.7元,平均每个月需要付多少元水费?
21.文具店的英语本和数学本的价格相同,王芳买了5本英语本和4本数学本,每本1.8元。她带了10元钱,够用吗?(填够用或不够用)
22.一块梯形草地面积是450m2,梯形的下底是30m,上底的长度是下底的一半,这块梯形草地的高是多少米?
23.一块长方形广告牌长9.2米、宽5米,用油漆刷这块广告牌的一面,每平方米用油漆0.76千克,已知每桶油漆净重15千克。
(1)刷这块广告牌要用油漆多少千克?
(2)至少需要买回多少桶油漆?
24.三角形ABC三个顶点的位置用数对表示分别为A(2,1)、B(6,1)、C(4,7)。
(1)请将三角形ABC画在方格图中。
(2)三角形ABC的面积是( )cm2。(每个小方格的边长是1cm)
(3)以AB为底,画出一个与这个三角形面积相等的平行四边形。
25.科技书有55本,比故事书的3倍少14本。故事书有多少本?(用方程解答)
26.一套桌椅的售价是280元,已知桌子的单价是椅子的3倍,桌子和椅子的单价分别是多少元?
27.一块平行四边形的牌匾,底是20.2米,高是4.2米,给这块牌匾刷上油漆,每平方米用油漆0.6千克,需要多少千克油漆?
28.甲乙两车从A、B两地同时相向开出,甲车每小时行54千米,乙车每小时行60千米。两车相遇时,乙车比甲车多行了18千米,A、B两地相距多少千米?
29.如图是一块梯形菜地的示意图,张大伯把它分成一个平行四边形和一个三角形.平行四边形地里种大白菜,三角形地里种萝卜.
(1)每棵大白菜占地0.16m ,一共可以种多少棵?
(2)萝卜地一共有多少平方米?
30.葡萄每千克4.5元,苹果每千克4.1元,小丽付20元够吗?
31.为鼓励居民节约用电,重庆市电力公司制订下列收费办法:每户每月用电100度以内(含100度),1.8元/度。超出100度部分,按2.5元/度收取。
(1)小明家九月份用电120度,该交电费多少元?
(2)小红家十月份交电费225元,她家十月份用电多少度?
32.3台洒水车,0.4小时可以喷洒地面3.6公顷。照这样计算,一台洒水车1小时可喷洒多少公顷?
33.有两桶油,甲桶油的质量是乙桶油的1.8倍,如果从甲桶中取出1.2千克油倒入乙桶油中,两桶油的质量就相等了。原来两桶中各有油多少千克?(列方程解答)
34.沙茶面是福建省厦门市的一道传统小吃,某餐饮店在假期推出了以下三种套餐。
A套餐 B套餐 C套餐
16.5元/份 24.8元/份 20.6元/份
某旅游团在该店吃沙茶面,用500元买了16份A套餐,剩下的钱最多还能买多少份B套餐?
35.小明妈妈带了100元钱,打算买13千克苹果和9千克桃子,钱够吗?
36.下面每个小方格的边长都表示1厘米,请你按要求画图。
(1)画出一个面积是15平方厘米的平行四边形。
(2)画一个面积是12平方厘米、高是3厘米的梯形。
(3)用数对表示平行四边形各个顶点的位置。
37.张叔叔选择的上网收费标准是:每月缴费30元可以上网50小时,超过50小时每小时收费1.2元。张叔叔12月份上网90小时,需要缴纳多少元上网费?
38.一个梯形草地中间有一块三角形空地,其它地方都植有小草(如右图,单位:m)。植草部分的面积是多少平方米
39.学学和乐乐两人比赛射箭,每一局,胜利的一方得5分,输掉的一方减2分,平局则两人各得3分。比赛10局后,两人的分数之和为48分。那么,比赛中有多少局胜负局?
40.乐乐今年8岁,妈妈今年36岁。乐乐多少岁时,妈妈的年龄是乐乐年龄的3倍?(用方程解答)
参考答案:
1.(1)(6,2);(2,4);(4,6);(6,7)
(2)见详解
【分析】(1)根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数在前,行数在后。据此解答;
(2)根据利用方向和距离表示确定物体位置的方法,先确定方向,再确定距离。据此解答。
【详解】(1)超市的位置用数对表示是(6,2),图书馆的位置用数对表示是(2,4),广场的位置用数对表示是(4,6),公园的位置用数对表示是(6,7)。
(2)小正方形的边长是100米,书店在学校以北100m,再往东走600m处,由此可知,书店的位置用数对表示是(9,2)。
作图如下:
【点睛】此题考查的目的是理解掌握利用数对表示物体位置的方法,利用方向和距离确定物体位置的方法及应用。
2.(1)学校(4,7),超市(7,9),青年广场(5,5),花店(8,2)
(2)见详解
【分析】(1)根据用数对表示位置的方法,结合学校、超市、青年广场、花店分别所在的行数和列数,解题即可;
(2)根据温馨小区和银行的数对位置,在图上找出对应点即可。
【详解】(1)学校(4,7),超市(7,9),青年广场(5,5),花店(8,2)
(2)
【点睛】本题考查了用数对表示位置,属于基础题,解题时细心即可。
3.35.04千瓦时
【分析】用12×0.008先求出1天的耗电量,再乘365即可求出电视机一年的耗电量。
【详解】12×0.008×365
=0.096×365
=35.04(千瓦时)
答:一台电视机一年(按365天计算)在这一项上要耗电35.04千瓦时。
【点睛】本题主要考查小数连乘的简单应用。
4.40元
【分析】由题意可知,不足1千克的按1千克计算,所以8.2千克按照9千克计算,根据单价×数量=总价,先求出超过5千克的钱数,再加上20元即可求解。
【详解】(9-5)×5+20
=4×5+20
=20+20
=40(元)
答:应付快递费40元。
【点睛】本题考查单价、数量和总价,求出超过5千克的钱数是解题的关键。
5.32元
【详解】略
6.1.5元
【分析】用垃圾处理费的总钱数除以房子的建筑面积即可。
【详解】102.3÷68.2=1.5(元)
答:小区的垃圾处理费每年每平方米1.5元。
【点睛】此题考查小数除法的计算,认真解答即可。
7.(1)42.5元
(2)7千克
【分析】(1)13.8千克≈14千克;先用14千克-1千克,求出超出1千克的部分的重量,再乘2.5,求出超出部分需要付的钱数,再加上1千克以内的10元,即可求出需要支付的钱数;
(2)用一共付的钱数-10元,求出超出1千克需要支付的钱数,再用超出部分支付的钱数÷2.5,求出超出1千克部分的重量,再加上1千克,即可求出这些物品的重量。
【详解】(1)13.8千克≈14千克
10+(14-1)×2.5
=10+13×2.5
=10+32.5
=42.5(元)
答:需要支付42.5元。
(2)(25-10)÷2.5+1
=15÷2.5+1
=6+1
=7(千克)
答:这些物品最多重7千克。
8.够
【分析】利用加法求出一共有多少人需要乘车,再将总人数除以每辆车的限乘人数,利用进一法将商保留到整数部分,求出至少需要多少辆车,从而判断10辆车是否够用。
【详解】(400+36)÷45
=436÷45
≈10(辆)
答:租10辆车够。
【点睛】本题考查了商的近似数,能根据实际情况采用进一法是解题的关键。
9.4.2万块
【分析】用8.4÷3.5求出按时运完的时间,减去0.4小时即可求出提前运完的时间,再用砖的总块数除以提前运完的时间即可求出每小时需要运多少万块。
【详解】
=8.4÷2
=4.2(万块);
答:每小时需要运4.2万块。
【点睛】先求出提前运完的时间是解答本题的关键,再用总块数除以提前运完的时间即可解答。
10.160秒
【详解】60÷(4 – 1)×(12 – 4)= 160(秒)
11.80平方厘米
【详解】试题分析:根据平行四边形的面积公式:s=ah,已知平行四边形底面积和高,首先求出平行四边形的底,进而求出阴影部分三角形的底,再根据三角形的面积公式:s=ah,把数据代入公式解答.
解:240÷8=30(厘米),
(30﹣10)×,
=20×,
=80(平方厘米),
答:阴影部分的面积是80平方厘米.
点评:此题主要考查平行四边形、三角形的面积公式的灵活运用.
12.(1)a-25b;(2)68页
【分析】(1)用书的总页数减去已经看的,将还剩下多少没看表示出来;
(2)将a和b具体的值代入(1)中的式子,求出具体还剩下多少页没有看。
【详解】(1)还剩下(a-25b)页没有看;
(2)a-25b
=243-25×7
=243-175
=68(页)
答:还剩下68页没看。
【点睛】本题考查了含有字母式子的化简和求值,有一定运算能力是解题的关键。
13.①152平方米;②9120元
【分析】①观察图形可知,草坪的面积等于梯形的面积减去中间长方形的面积,根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据进行计算即可;②根据题意可知,每平方米种植12棵草,每棵草5元钱,要求种植这块草坪需要多少元钱,我们可以用每平方米种植的草的棵数乘草坪的面积,求出一共种植的草的数量,再用每棵草的价钱乘种植的草的数量,即可解答。
【详解】①由题意得:
(10+24)×10÷2
=34×10÷2
=340÷2
=170(平方米)
6×3=18(平方米)
170-18=152(平方米)
答:草坪的面积是152平方米。
②由题意得:
12×152×5
=1824×5
=9120(元)
答:这块草坪需要9120元。
14.72平方分米
【详解】试题分析:观察图形可知:图中有平行四边形ADEF,长方形ABCF,等腰直角三角形ABD和CDG;而阴影部分是一个梯形:只要求出这个梯形的上下底CG、AB和高BC的长度即可解答问题.
解:AB的长度是:90÷6=15(分米),
则BD的长度也是15分米,
因为BC=AF=6分米,
所以CD=DG=15﹣6=9(分米),
所以阴影部分的面积是:(9+15)×6÷2,
=24×3,
=72(平方分米);
答:阴影部分的面积是72平方分米.
点评:此题要充分利用图中已知的平行四边形、长方形、等腰直角三角形的性质进行解答.
15.18.3千米
【分析】根据路程=时间×速度,列式即可。
【详解】30.5×0.6=18.3(千米)
答:0.6小时航行18.3千米。
【点睛】关键是理解速度、时间、路程之间的关系,掌握小数乘小数的计算方法。
16.①玩具小狗2只; ②玩具小狗1只,玩具小熊1只 ;③玩具小熊2只
【解析】略
17.497.2元
【分析】根据求一个数的几倍是多少,用乘法计算,用5.5乘1.4即可求出每根跳绳的钱数,再根据单价×数量=总价,据此求出40个毽子和36根跳绳的钱数,然后再相加即可。
【详解】5.5×1.4×36+5.5×40
=7.7×36+5.5×40
=277.2+220
=497.2(元)
答:一共花了497.2元。
【点睛】本题考查小数乘法,明确单价、数量和总价之间的关系是解题的关键。
18.不能
【分析】根据速度×时间=路程,用62乘4.5即可求出甲地和乙地之间的路程,再根据路程÷速度=时间,据此求出每小时行驶75千米时所用的时间,再与3.5对比即可。
【详解】62×4.5=279(千米)
279÷75=3.72(小时)
3.72>3.5
答:3.5小时不能到达。
【点睛】本题考查小数乘除法,明确路程、速度和时间之间的关系是解题的关键。
19.5千米
【分析】首先用小明从家打车去图书馆共付的钱数减去起步价,求出超过起步价的费用是多少;然后用超过起步价的费用除以3千米以外每千米的收费,求出超过3千米的路程是多少,再加上3千米,即求出他家到图书馆的最远距离。
【详解】(11.6-8)÷1.8+3
=3.6÷1.8+3
=2+3
=5(千米)
答:他家到图书馆最远是5千米。
【点睛】解答此题的关键是求出超过起步价的费用,以及超过3千米的路程是多少。
20.34.29元
【分析】根据总价=单价×数量,将数据代入,先算出淘气家上半年付的水费,再除以月数,即可得出答案。
【详解】半年有6个月。
76.2×2.7÷6
=205.74÷6
=34.29(元)
答:平均每个月需要付34.29元。
【点睛】本题考查学生对小数乘除法的掌握和运用。
21.不够
【分析】因为两种本子的价钱相同,所以先求出英语本和数学本的总本数,再乘每本的价钱,求出花费的总钱数,再与带的钱数比较大小。
【详解】(5+4)×1.8
=9×1.8
=16.2(元)
16.2>10
答:不够用。
【点睛】本题考查经济问题,先求出总数量,再根据总价、单价和数量之间的关系解答。
22.20米
【分析】根据“梯形面积=(上底+下底)×高÷2”,得“高=梯形面积×2÷(上底+下底)”,据此计算得解。
【详解】450×2÷(30+30÷2)
=900÷(30+15)
=900÷45
=20(米)
答:这块梯形草地的高是20米。
【点睛】本题考查梯形面积,关键是熟练掌握梯形面积公式,并会运用逆运算对公式进行变形,本题也可列方程求解。
23.(1)34.96千克
(2)3桶
【分析】(1)利用长方形面积公式:S=ab计算长方形广告牌的面积,再乘每平方米所需油漆的质量,求出所需油漆的质量即可;
(2)根据(1)的结果,用所需油漆的质量除以每桶油漆的质量,求油漆的桶数。商不是整数时,利用进一法保留整数。
【详解】(1)9.2×5=46(平方米)
46×0.76=34.96(千克)
答:刷这块广告牌要用油漆34.96千克。
(2)34.96÷15≈2.33≈3(桶)
答:至少需要买回3桶油漆。
24.(1)(3)图见详解
(2)12
【分析】(1)用数对表示位置时,括号里第一个数字表示列,第二个数字表示行,据此找到点的位置,再将各点一次连接成图形即可。
(2)数出三角形底和高的方格数,可以知道它们的长度,再根据三角形面积=底×高÷2,进行计算即可。
(3)平行四边形面积=底×高,底不变与它面积相等的三角形的高是平行四边形高的2倍,据此解答。
【详解】(2)4×6÷2=12(cm2)
三角形ABC的面积是12cm2。
(3)由分析得:6÷2=3(cm)
以AB为底,画出一个与这个三角形面积相等的平行四边形的高为3cm。
(1)(3)如下图:
25.23本
【分析】根据题干可得等量关系:故事书的3倍-14本=科技书的本数,据此设故事书有x本,列出方程解决问题。
【详解】解:设故事书有x本。
3x-14=55
3x=55+14
3x=69
x=23
答:故事书有23本。
【点睛】解答此题容易找出基本数量关系:故事书的3倍-14本=科技书的本数,由此列方程解决问题。
26.桌子210元;椅子70元
【分析】首先假设椅子的单价是x元,根据已知桌子的单价是椅子的3倍,所以桌子的单价就是3x元,一套桌椅的售价是280元就是一张桌子加上一把椅子的价格,也是桌子的单价加上椅子的单价,即3x加上x等于280,通过解方程求出x,求出的x就是椅子的单价,再用x的值与3相乘,就是桌子的单价。据此解答即可。
【详解】解:设椅子的单价是x元,桌子的单价是3x元。
x+3x=280
4x=280
4x÷4=280÷4
x=70
3x=3×70=210(元)
答:桌子的单价是210元,椅子的单价是70元。
27.50.904千克
【详解】20.2×4.2×0.6
=84.84×0.6
=50.904(千克)
答:需要50.904千克油漆.
28.342千米
【分析】把相遇时间设为未知数,等量关系式:乙车速度×相遇时间-甲车速度×相遇时间=乙车比甲车多行驶的路程,解方程求出相遇时间,最后根据“相遇时间×速度和=总路程”求出A、B两地之间的总路程,据此解答。
【详解】解:设经过x小时相遇。
60x-54x=18
6x=18
x=18÷6
x=3
(54+60)×3
=114×3
=342(千米)
答:A、B两地相距342千米。
【点睛】本题主要考查相遇问题,找出等量关系式并列方程求出相遇时间是解答题目的关键。
29.(1)180棵;(2)10.8平方米
【详解】(1)6.4×4.5÷0.16=180(棵)
(2)(11.2-6.4)×4.5÷2=10.8(平方米)
30.不够
【详解】4.5×3.6+4.1=20.3(元) 20.3元>20元 答:小丽付20元不够.
31.(1)230元;(2)118度
【分析】(1)由题意可知,超过100度的部分有(120-100)度,根据电费单价×用电量=总价,据此求出超过100度的部分的价钱,100度的电费是(100×1.8)元,然后把这两部分的钱数加起来即可得解;
(2)100度的电费是(100×1.8)元,等于180元,用十月份的电费减去180元即可求出超过100度部分的电费,再根据总价÷电费单价=用电量,据此求出超过100度部分的用电量,再加上100度,即可求出小红家十月份用电的度数。
【详解】(1)100×1.8+(120-100)×2.5
=180+20×2.5
=180+50
=230(元)
答:该交电费230元。
(2)(225-100×1.8)÷2.5+100
=(225-180)÷2.5+100
=45÷2.5+100
=18+100
=118(度)
答:她家十月份用电118度。
【点睛】本题考查分段计费问题,利用小数乘除法的计算法则,明确总价、用电量和单价之间的关系是解题的关键。
32.3公顷
【分析】喷洒地面面积÷时间=1小时3台洒水车喷洒面积,再除以3就是一台洒水车1小时可喷洒面积。
【详解】3.6÷0.4÷3=3(公顷)
答:一台洒水车1小时可喷洒3公顷。
【点睛】关键是掌握小数除法的计算方法。
33.甲桶有油5.4千克,乙桶有油3千克
【分析】根据题意,可知“甲桶油的质量=乙桶油的质量×1.8”“ 甲桶油的质量-1.2=乙桶油的质量+1.2”,据此列方程解答即可。
【详解】解:设乙桶有油x千克,则甲桶有油1.8x千克;
1.8x-1.2=x+1.2
0.8x=2.4
x=3;
3×1.8=5.4(千克);
答:甲桶有油5.4千克,乙桶有油3千克。
【点睛】根据甲桶和乙桶油的倍数关系设出未知量,根据变化后质量相等列方程解答。
34.9份
【分析】已知每份A套餐16.5元,买了16份,根据“总价=单价×数量”,求出买A套餐的总花费;再用总钱数减去买A套餐的总花费,就是剩下的钱数;
已知每份B套餐24.8元,求用剩下的钱数最多还能买几份B套餐,根据“数量=总价÷单价”,得数采用“去尾法”保留整数,即可求解。
【详解】A套餐共花费:16.5×16=264(元)
还剩下:500-264=236(元)
最多还能买B套餐:236÷24.8≈9(份)
答:剩下的钱最多还能买9份B套餐。
35.够
【详解】4.8×13+3.45×9
=62.4+31.05
=93.45(元)
100>93.45,够.
答:钱够.
36.(1)见详解
(2)见详解
(3)A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【分析】(1)根据平行四边形的面积计算公式找出符合条件的底和高;
(2)根据梯形的面积和高,找出出上底和下底的关系,计算符合条件的上下底;
(3)数对表示位置的方法:先写列数再写行数,中间用逗号隔开,如:(列数,行数),括号前面标注点的名称即可。
【详解】(1)平行四边形面积为15平方厘米,则底为5厘米,高为3厘米(答案不唯一)
(2)梯形的面积是12平方厘米、高是3厘米,上底+下底=12×2÷3=8(厘米),上底为2厘米,下底为6厘米(答案不唯一)
(3)平行四边形各顶点位置表示为:A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【点睛】灵活运用平行四边形和梯形的面积公式是解答题目的关键。
37.78元
【分析】张叔叔上网时间超过50小时,先求出超出50小时的小时数,超出部分×对应收费标准+50小时内的费用=需要缴纳的上网费,据此列式解答。
【详解】30+(90-50)×1.2
=30+40×1.2
=30+48
=78(元)
答:需要缴纳78元上网费。
【点睛】关键是理解收费标准,掌握小数乘法的计算方法。
38.12平方米
【详解】(6+10)×4÷2=32(平方米)
4×10÷2=20(平方米)
32-20=12(平方米)
答:植草部分的面积是12平方米。
39.4局
【分析】假设比赛中有x局胜负局,则有平局(10-x)局,每一场胜负局两人的得分之和是(5-2)分,每一场平局两人的得分之和是3×2=6分,根据数量关系:每一场胜负局两人的得分之和×胜负局的场数+每一场平局两人的得分之和×平局的场数=48,据此列出方程,求解即可。
【详解】解:设比赛中有x局胜负局,则有平局(10-x)局,
(5-2)×x+3×2×(10-x)=48
3x+6×(10-x)=48
60-3x=48
3x=60-48
3x=12
x=4
答:比赛中有4局胜负局。
【点睛】此题属于鸡兔同笼的应用题,采用列方程的方法,解题关键是弄清题意,把胜负局的场数设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
40.14岁
【分析】年龄问题中,乐乐和妈妈的年龄差一直不变,即等量关系式为: 3倍时候妈妈年龄-乐乐的年龄=今年妈妈的年龄-今年乐乐的年龄,据此列出方程即可求解。
【详解】解:设乐乐x岁时,妈妈的年龄是乐乐的3倍。
3x-x=36-8
2x=28
2x÷2=28÷2
x=14
答:当乐乐14岁时,妈妈的年龄是乐乐的3倍。
【点睛】此题考查年龄问题,抓住年龄差不变是解题的关键,举例说明:今年小明年龄10岁,妈妈今年35岁,年龄差为35-10=25岁,2年后小明12岁,妈妈37岁,年龄差还是为37-12=25岁,所以年龄差一直不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
