人教版2024七年级下册数学 7.2.1 平行线的概念 教学设计(含巩固练习)
文档属性
| 名称 | 人教版2024七年级下册数学 7.2.1 平行线的概念 教学设计(含巩固练习) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 10:28:26 | ||
图片预览


文档简介
7.2.1平行线的概念 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第七章“相交线与平行线”7.2.1平行线的概念,内容包括:理解平行线的概念;能用三角板和直尺过已知直线外一点画这条直线的平行线;掌握平行线的基本事实:过直线外一点有且只有一条直线与这条直线平行;了解平行于同一条直线的两条直线平行.
2.内容解析
本节课的学习内容是平行线的概念, 关于平行线的基本事实及其推论.这是在研究了两条直线相交的基础上进行的,是进一步研究平行关系、平行线的性质和判定, 进一步认识三角形、平行四边形、梯形等图形的特征的基础.
基于以上分析,确定本节课的教学重点为:理解平行线的概念;掌握平行线的基本事实及其推论.
二、目标和目标解析
1.目标
(1)理解平行线的概念;能用三角板和直尺过已知直线外一点画这条直线的平行线;掌握平行线的基本事实:过直线外一点有且只有一条直线与这条直线平行;了解平行于同一条直线的两条直线平行.
(2)经历动手操作、观察、归纳平行线的概念及平行线的基本事实的过程,提高观察归纳、动手操作、空间想象及逻辑思维能力.
(3)会利用所学知识进行简单的推理,感受数学语言的简洁美,并能将学到的知识应用到生活中去,提高应用意识.
2.目标解析
在本节课的学习中,学生从一条直线分别与两条直线相交出发,通过转动木条,观察理解平行线的概念,在这个过程中感悟“从一般到特殊”的数学研究路径. 学生在动手操作、观察、归纳的过程中,体会关于平行线的基本事实及其推论,逐步提高空间想象能力和逻辑思维能力,为今后的几何学习打下基础.
学生从实际问题中抽象出平行线模型,再用数学知识解决实际问题,在这个过程中逐步提高数学应用能力和数学建模的核心素养.
三、教学问题诊断分析
学习平行线的相关知识,难点主要在以下方面.
概念上,理解“在同一平面内”这一条件易出错,因为在空间中不相交的直线不一定平行,这就需要学生具备一定的空间想象能力.在日常生活中,空间物体干扰认知,学生很难直观地看到纯粹的平面内的直线关系,而且视觉上近似平行的直线可能存在微小夹角,这也影响对平行线概念的准确把握.
关于平行线的基本事实中,理解“过直线外一点”和“有且只有”也需要学生具备较强的逻辑思维能力.
基于以上分析,确定本节课的教学难点为:理解平行线的概念;掌握平行线的基本事实.
四、教学过程设计
(一)复习引入
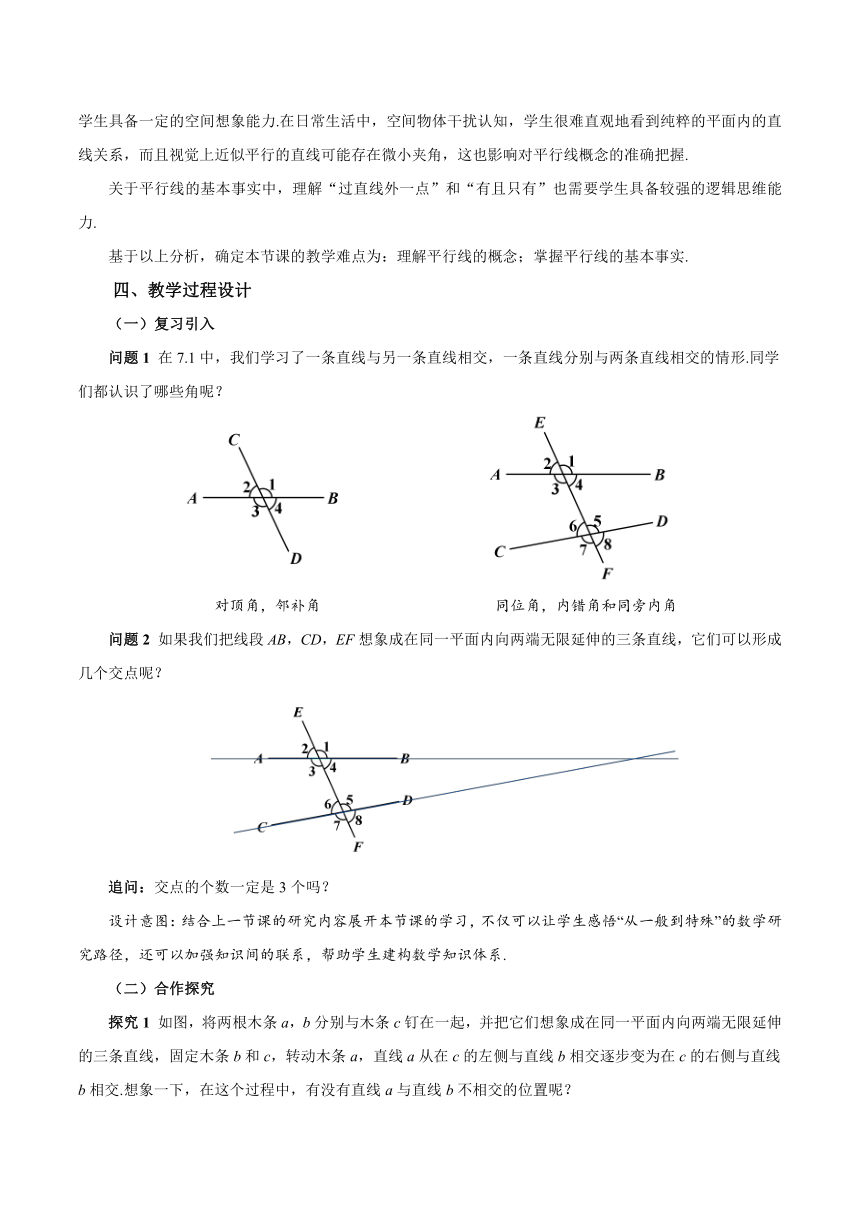
问题1 在7.1中,我们学习了一条直线与另一条直线相交,一条直线分别与两条直线相交的情形.同学们都认识了哪些角呢?
对顶角,邻补角 同位角,内错角和同旁内角
问题2 如果我们把线段AB,CD,EF想象成在同一平面内向两端无限延伸的三条直线,它们可以形成几个交点呢?
追问:交点的个数一定是3个吗?
设计意图:结合上一节课的研究内容展开本节课的学习,不仅可以让学生感悟“从一般到特殊”的数学研究路径,还可以加强知识间的联系,帮助学生建构数学知识体系.
(二)合作探究
探究1 如图,将两根木条a,b分别与木条c钉在一起,并把它们想象成在同一平面内向两端无限延伸的三条直线,固定木条b和c,转动木条a,直线a从在c的左侧与直线b相交逐步变为在c的右侧与直线b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
【视频演示转动过程】
平行线
在同一平面内,当直线a,b不相交时,我们说直线a与b互相平行,记作a∥b.
追问:在同一平面内,不重合的两条直线有几种位置关系?
答:相交与平行.
问题3 在实际生活中,平行线随处可见.你能举出一些例子吗?
探究2 借助直尺和三角尺,你能画出直线a的平行线吗?
1.放,2.靠,3.推,4.画.
问题4 如图,过点B画直线a的平行线,能画出几条?过点C呢?
答:过点B画直线a的平行线,只能画出1条. 过点C画直线a的平行线,也只能画出1条.
问题5 在图中转动木条a的过程中,有几个位置使得直线a与b平行?
答:只有一个位置使得直线a与b平行.
关于平行线的基本事实
过直线外一点有且只有一条直线与这条直线平行.
推论
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
如果b∥a,c∥a,那么b∥c.
设计意图:使用视频对转动过程进行动态演示,可以使变化过程可视化,化抽象为形象.利用多媒体动态演示借助直尺和三角尺画平行线的步骤,可以更加清晰规范的向学生展示绘图过程.
(三)典例分析
1. 如图,用直尺和三角尺画平行线:
(1)过点A画MN∥BC;
(2)过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.
(1) (2)
2. 观察如图所示的长方体,用符号表示下列两条棱的位置关系:
A1B1 ∥ AB,AA1 ⊥ AB,A1D1 ⊥ D1C1,AD ∥ BC.
追问:你能在教室里找到这些位置关系的实例吗?与同学讨论一下.
(四)巩固练习
1. 判断下列说法是否正确.
(1)在同一平面内,不相交的两条射线是平行线.( × )
(2)在同一平面内,不相交的两条线段是平行线.( × )
(3)不相交的两条直线是平行线. ( × )
(4)一条直线的平行线有且只有一条. ( × )
(5)过一点有且只有一条直线与已知直线平行. ( × )
2. 同一平面内,不重合的两条直线的位置关系有( B )
A.相交、垂直 B.相交、平行 C.垂直、平行 D.相交、垂直、平行
3. 在同一个平面内,直线a、b相交于点P,a∥c,则b与c的位置关系是( B )
A.平行 B.相交 C.重合 D.平行或相交
4. 下列说法中:
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
②直线外一点到这条直线的垂线段叫做点到直线的距离;
③过一点有且只有一条直线平行于已知直线;
④过一点有且只有一条直线垂直于已知直线.
其中正确的个数有( A )
A.1个 B.2个 C.3个 D.4个
5. 四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那直线a,d的位置关系为__a∥d__.
6.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
解:因为CD∥EF,EF∥AB,所以CD∥AB.
7. 如图,在∠AOB内取一点P,过点P画PC∥OA交OB于点C,画PD∥OB交OA于点D.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
归纳总结
感受中考
1. (2024 常州) 如图,推动水桶,以点O为支点,使其向右倾斜.若在点A处分别施加推力F1、F2,则F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是( A )
A.垂线段最短 B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线 D.过直线外一点有且只有一条直线与已知直线平行
2. (2010 柳州)三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是( B )
A.a⊥b B.a∥b C.a⊥b或a∥b D.无法确定
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(七)小结梳理
(八)布置作业
1.必做题:习题7.2 第1题.
2.探究性作业:
在同一平面内有4条不重合的直线,它们可以把这个平面分成几部分?
(小组讨论探究,整理研究成果,选出代表课前交流.)
五、教学反思
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第七章“相交线与平行线”7.2.1平行线的概念,内容包括:理解平行线的概念;能用三角板和直尺过已知直线外一点画这条直线的平行线;掌握平行线的基本事实:过直线外一点有且只有一条直线与这条直线平行;了解平行于同一条直线的两条直线平行.
2.内容解析
本节课的学习内容是平行线的概念, 关于平行线的基本事实及其推论.这是在研究了两条直线相交的基础上进行的,是进一步研究平行关系、平行线的性质和判定, 进一步认识三角形、平行四边形、梯形等图形的特征的基础.
基于以上分析,确定本节课的教学重点为:理解平行线的概念;掌握平行线的基本事实及其推论.
二、目标和目标解析
1.目标
(1)理解平行线的概念;能用三角板和直尺过已知直线外一点画这条直线的平行线;掌握平行线的基本事实:过直线外一点有且只有一条直线与这条直线平行;了解平行于同一条直线的两条直线平行.
(2)经历动手操作、观察、归纳平行线的概念及平行线的基本事实的过程,提高观察归纳、动手操作、空间想象及逻辑思维能力.
(3)会利用所学知识进行简单的推理,感受数学语言的简洁美,并能将学到的知识应用到生活中去,提高应用意识.
2.目标解析
在本节课的学习中,学生从一条直线分别与两条直线相交出发,通过转动木条,观察理解平行线的概念,在这个过程中感悟“从一般到特殊”的数学研究路径. 学生在动手操作、观察、归纳的过程中,体会关于平行线的基本事实及其推论,逐步提高空间想象能力和逻辑思维能力,为今后的几何学习打下基础.
学生从实际问题中抽象出平行线模型,再用数学知识解决实际问题,在这个过程中逐步提高数学应用能力和数学建模的核心素养.
三、教学问题诊断分析
学习平行线的相关知识,难点主要在以下方面.
概念上,理解“在同一平面内”这一条件易出错,因为在空间中不相交的直线不一定平行,这就需要学生具备一定的空间想象能力.在日常生活中,空间物体干扰认知,学生很难直观地看到纯粹的平面内的直线关系,而且视觉上近似平行的直线可能存在微小夹角,这也影响对平行线概念的准确把握.
关于平行线的基本事实中,理解“过直线外一点”和“有且只有”也需要学生具备较强的逻辑思维能力.
基于以上分析,确定本节课的教学难点为:理解平行线的概念;掌握平行线的基本事实.
四、教学过程设计
(一)复习引入
问题1 在7.1中,我们学习了一条直线与另一条直线相交,一条直线分别与两条直线相交的情形.同学们都认识了哪些角呢?
对顶角,邻补角 同位角,内错角和同旁内角
问题2 如果我们把线段AB,CD,EF想象成在同一平面内向两端无限延伸的三条直线,它们可以形成几个交点呢?
追问:交点的个数一定是3个吗?
设计意图:结合上一节课的研究内容展开本节课的学习,不仅可以让学生感悟“从一般到特殊”的数学研究路径,还可以加强知识间的联系,帮助学生建构数学知识体系.
(二)合作探究
探究1 如图,将两根木条a,b分别与木条c钉在一起,并把它们想象成在同一平面内向两端无限延伸的三条直线,固定木条b和c,转动木条a,直线a从在c的左侧与直线b相交逐步变为在c的右侧与直线b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
【视频演示转动过程】
平行线
在同一平面内,当直线a,b不相交时,我们说直线a与b互相平行,记作a∥b.
追问:在同一平面内,不重合的两条直线有几种位置关系?
答:相交与平行.
问题3 在实际生活中,平行线随处可见.你能举出一些例子吗?
探究2 借助直尺和三角尺,你能画出直线a的平行线吗?
1.放,2.靠,3.推,4.画.
问题4 如图,过点B画直线a的平行线,能画出几条?过点C呢?
答:过点B画直线a的平行线,只能画出1条. 过点C画直线a的平行线,也只能画出1条.
问题5 在图中转动木条a的过程中,有几个位置使得直线a与b平行?
答:只有一个位置使得直线a与b平行.
关于平行线的基本事实
过直线外一点有且只有一条直线与这条直线平行.
推论
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
如果b∥a,c∥a,那么b∥c.
设计意图:使用视频对转动过程进行动态演示,可以使变化过程可视化,化抽象为形象.利用多媒体动态演示借助直尺和三角尺画平行线的步骤,可以更加清晰规范的向学生展示绘图过程.
(三)典例分析
1. 如图,用直尺和三角尺画平行线:
(1)过点A画MN∥BC;
(2)过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.
(1) (2)
2. 观察如图所示的长方体,用符号表示下列两条棱的位置关系:
A1B1 ∥ AB,AA1 ⊥ AB,A1D1 ⊥ D1C1,AD ∥ BC.
追问:你能在教室里找到这些位置关系的实例吗?与同学讨论一下.
(四)巩固练习
1. 判断下列说法是否正确.
(1)在同一平面内,不相交的两条射线是平行线.( × )
(2)在同一平面内,不相交的两条线段是平行线.( × )
(3)不相交的两条直线是平行线. ( × )
(4)一条直线的平行线有且只有一条. ( × )
(5)过一点有且只有一条直线与已知直线平行. ( × )
2. 同一平面内,不重合的两条直线的位置关系有( B )
A.相交、垂直 B.相交、平行 C.垂直、平行 D.相交、垂直、平行
3. 在同一个平面内,直线a、b相交于点P,a∥c,则b与c的位置关系是( B )
A.平行 B.相交 C.重合 D.平行或相交
4. 下列说法中:
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
②直线外一点到这条直线的垂线段叫做点到直线的距离;
③过一点有且只有一条直线平行于已知直线;
④过一点有且只有一条直线垂直于已知直线.
其中正确的个数有( A )
A.1个 B.2个 C.3个 D.4个
5. 四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那直线a,d的位置关系为__a∥d__.
6.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
解:因为CD∥EF,EF∥AB,所以CD∥AB.
7. 如图,在∠AOB内取一点P,过点P画PC∥OA交OB于点C,画PD∥OB交OA于点D.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
归纳总结
感受中考
1. (2024 常州) 如图,推动水桶,以点O为支点,使其向右倾斜.若在点A处分别施加推力F1、F2,则F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是( A )
A.垂线段最短 B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线 D.过直线外一点有且只有一条直线与已知直线平行
2. (2010 柳州)三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是( B )
A.a⊥b B.a∥b C.a⊥b或a∥b D.无法确定
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(七)小结梳理
(八)布置作业
1.必做题:习题7.2 第1题.
2.探究性作业:
在同一平面内有4条不重合的直线,它们可以把这个平面分成几部分?
(小组讨论探究,整理研究成果,选出代表课前交流.)
五、教学反思
同课章节目录
