2024-2025学年人教版八年级上册数学期末押题卷(含答案)
文档属性
| 名称 | 2024-2025学年人教版八年级上册数学期末押题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 316.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 10:48:35 | ||
图片预览


文档简介
2024-2025学年人教版八年级上册数学期末押题卷
考试时间:90分钟 满分:100分
一、单选题(共10题;共30分)
1.(3分)如图,三角形中,,是高,,,则的长为( )
A. B. C. D.
2.(3分)下列计算正确的是( )
A. B. C. D.
3.(3分)在中,为边的中线.若与的周长差为,,则的长为( )
A.5 B.11 C.5或8 D.5或11
4.(3分)如图,这是某正方形的房屋结构平面图,其中主卧与客卧也都是正方形,它们的边长分别为米,米,其面积之和比剩余面积(阴影部分)多4平方米.则主卧与客卧的周长差为( )
A.4米 B.6米 C.8米 D.10米
5.(3分)为了缅怀革命先烈,传承红色精神,青海省某学校九年级师生在清明节期间前往距离学校的烈士陵园扫墓.一部分师生骑自行车先走,过了后,其余师生乘汽车出发,结果他们同时到达;已知汽车的速度是骑车师生速度的2倍,设骑车师生的速度为.根据题意,下列方程正确的是( )
A. B. C. D.
6.(3分)已知a、b、c是△ABC的三边长,且满足,则△ABC的形状是 ( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.不能确定
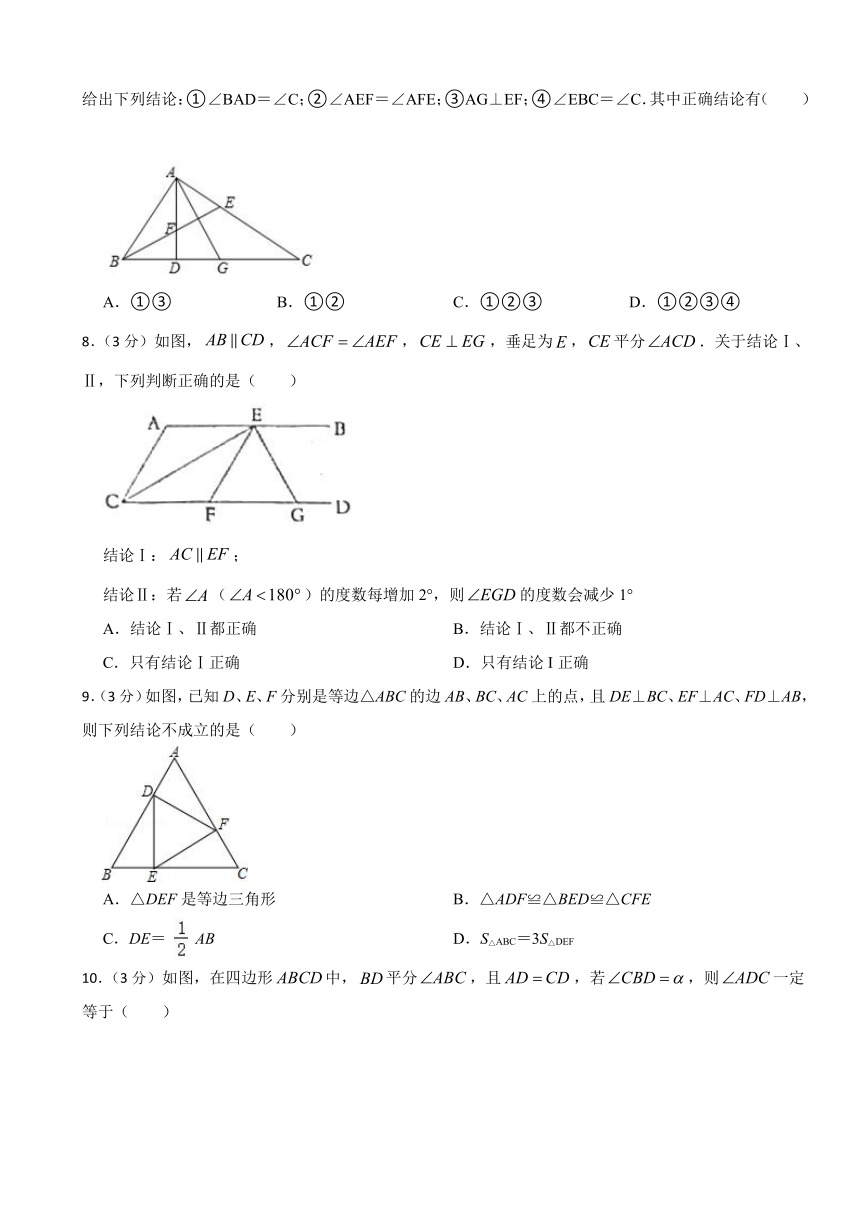
7.(3分)如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③AG⊥EF;④∠EBC=∠C.其中正确结论有( )
A.①③ B.①② C.①②③ D.①②③④
8.(3分)如图,,,,垂足为,平分.关于结论Ⅰ、Ⅱ,下列判断正确的是( )
结论Ⅰ:;
结论Ⅱ:若()的度数每增加2°,则的度数会减少1°
A.结论Ⅰ、Ⅱ都正确 B.结论Ⅰ、Ⅱ都不正确
C.只有结论Ⅰ正确 D.只有结论I正确
9.(3分)如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )
A.△DEF是等边三角形 B.△ADF≌△BED≌△CFE
C.DE= AB D.S△ABC=3S△DEF
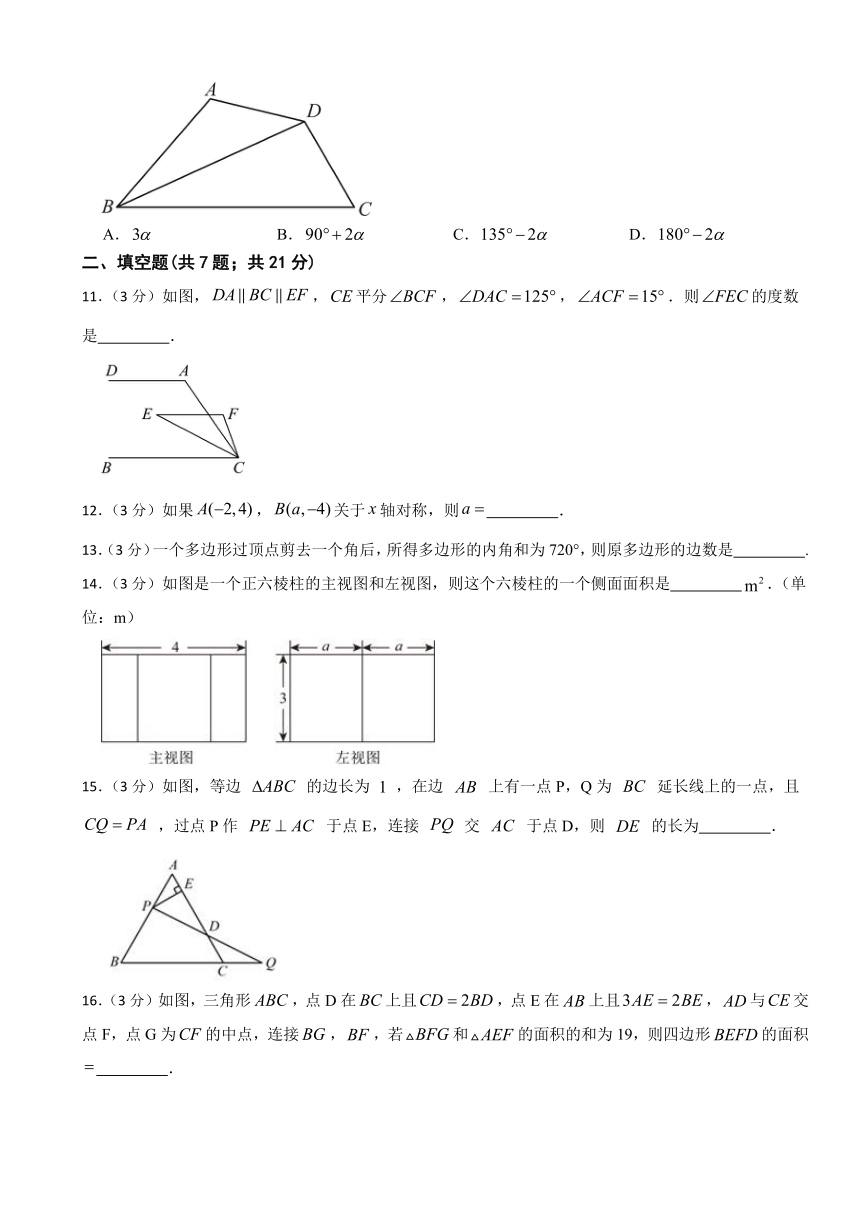
10.(3分)如图,在四边形中,平分,且,若,则一定等于( )
A. B. C. D.
二、填空题(共7题;共21分)
11.(3分)如图,,平分,,.则的度数是 .
12.(3分)如果,关于轴对称,则 .
13.(3分)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是 .
14.(3分)如图是一个正六棱柱的主视图和左视图,则这个六棱柱的一个侧面面积是 .(单位:m)
15.(3分)如图,等边 的边长为 ,在边 上有一点P,Q为 延长线上的一点,且 ,过点P作 于点E,连接 交 于点D,则 的长为 .
16.(3分)如图,三角形,点D在上且,点E在上且,与交点F,点G为的中点,连接,,若和的面积的和为19,则四边形的面积 .
17.(3分)如图,在 中, 平分 点 分别是 上的动点.若 则 的最小值是 .
三、解答题(共6题;共49分)
18.(6分)已知,求的值.
19.(7分)如图,分别是 的高和中线,若
(1)(3分)求的长.
(2)(4分)求 与的周长之差.
20.(8分)若一个正多边形的内角和加上它的外角和等于900°,求这个正多边形的边数与它每个内角的度数.
21.(8分)冰墩墩是2022年北京冬奥会的吉祥物,其敦厚、可爱的形象深入人心,制作的奥运纪念品很受大家喜爱。已知A型号的冰墩墩手办比B型号的冰墩墩钥匙扣的单价多30元,用880元购买A型号手办的数量是用290元购买B型号钥匙扣数量的2倍.
(1)(4分)求A,B两种型号纪念品的单价分别是多少元?
(2)(4分)若计划购买A,B两种型号的纪念品共100个,且所花费用不超过6800元,求最多能购买多少个A型号的纪念品?
22.(10分)某商店3月份购进一批T恤衫,进价合计12万元,因畅销,商店又于4月份购进一批同品牌T恤衫,进价合计15万元,数量是3月份的1.2倍,但每件进价涨了5元.
(1)(5分)3月份购进的T恤衫的单价是多少 4月份购进了多少件T恤衫
(2)(5分)这两批T恤衫开始都以每件180元出售,结果4月份后期出现滞销,还有一半的T恤衫没有售出,于是5月份商店便以定价的n折开始销售(n是正整数,且1≤n≤9),结果第二批T恤衫共盈利800m元(m为正整数).求m,n的值.
23.(10分)如图,在等边△ABC中,AB=6cm,动点P从点A出发以1cm/s的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.
(1)当t为何值时,△BPQ为直角三角形;
(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;
(3)求DE的长.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】
12.【答案】
13.【答案】6或7
14.【答案】6
15.【答案】
16.【答案】16
17.【答案】
18.【答案】9.
19.【答案】(1)
(2)1
20.【答案】解:设这个正多边形的边数为n,则根据题意,得:(n﹣2)×180°+360°=900°,
解得n=5, ;
答:这个多边形是正五边形,它每个内角的度数为108°.
21.【答案】(1)A型号的冰墩墩手办的单价为88元,B型号的冰墩墩钥匙扣的单价为58元
(2)33个
22.【答案】(1)解:设3月份购进的T恤衫的单价是x元,则4月份购进的T恤衫的单价是(x+5)元,
根据题意得:,
解得x=120,
经检验:x=120是原分式方程的解,
∴=1200件,
∴3月份购进的T恤衫的单价是120元,4月份购进了1200件T恤衫;
(2)解:4月份购进的T恤衫的单价为120+5=125元,
∴1200××(180-125)+1200××(180×-125)=800m,
整理得27n=2m+105,
∵m、n均为正整数,且1≤n≤9,
∴或或.
23.【答案】(1)2;(2)存在,t=3;(3)3cm
考试时间:90分钟 满分:100分
一、单选题(共10题;共30分)
1.(3分)如图,三角形中,,是高,,,则的长为( )
A. B. C. D.
2.(3分)下列计算正确的是( )
A. B. C. D.
3.(3分)在中,为边的中线.若与的周长差为,,则的长为( )
A.5 B.11 C.5或8 D.5或11
4.(3分)如图,这是某正方形的房屋结构平面图,其中主卧与客卧也都是正方形,它们的边长分别为米,米,其面积之和比剩余面积(阴影部分)多4平方米.则主卧与客卧的周长差为( )
A.4米 B.6米 C.8米 D.10米
5.(3分)为了缅怀革命先烈,传承红色精神,青海省某学校九年级师生在清明节期间前往距离学校的烈士陵园扫墓.一部分师生骑自行车先走,过了后,其余师生乘汽车出发,结果他们同时到达;已知汽车的速度是骑车师生速度的2倍,设骑车师生的速度为.根据题意,下列方程正确的是( )
A. B. C. D.
6.(3分)已知a、b、c是△ABC的三边长,且满足,则△ABC的形状是 ( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.不能确定
7.(3分)如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③AG⊥EF;④∠EBC=∠C.其中正确结论有( )
A.①③ B.①② C.①②③ D.①②③④
8.(3分)如图,,,,垂足为,平分.关于结论Ⅰ、Ⅱ,下列判断正确的是( )
结论Ⅰ:;
结论Ⅱ:若()的度数每增加2°,则的度数会减少1°
A.结论Ⅰ、Ⅱ都正确 B.结论Ⅰ、Ⅱ都不正确
C.只有结论Ⅰ正确 D.只有结论I正确
9.(3分)如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )
A.△DEF是等边三角形 B.△ADF≌△BED≌△CFE
C.DE= AB D.S△ABC=3S△DEF
10.(3分)如图,在四边形中,平分,且,若,则一定等于( )
A. B. C. D.
二、填空题(共7题;共21分)
11.(3分)如图,,平分,,.则的度数是 .
12.(3分)如果,关于轴对称,则 .
13.(3分)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是 .
14.(3分)如图是一个正六棱柱的主视图和左视图,则这个六棱柱的一个侧面面积是 .(单位:m)
15.(3分)如图,等边 的边长为 ,在边 上有一点P,Q为 延长线上的一点,且 ,过点P作 于点E,连接 交 于点D,则 的长为 .
16.(3分)如图,三角形,点D在上且,点E在上且,与交点F,点G为的中点,连接,,若和的面积的和为19,则四边形的面积 .
17.(3分)如图,在 中, 平分 点 分别是 上的动点.若 则 的最小值是 .
三、解答题(共6题;共49分)
18.(6分)已知,求的值.
19.(7分)如图,分别是 的高和中线,若
(1)(3分)求的长.
(2)(4分)求 与的周长之差.
20.(8分)若一个正多边形的内角和加上它的外角和等于900°,求这个正多边形的边数与它每个内角的度数.
21.(8分)冰墩墩是2022年北京冬奥会的吉祥物,其敦厚、可爱的形象深入人心,制作的奥运纪念品很受大家喜爱。已知A型号的冰墩墩手办比B型号的冰墩墩钥匙扣的单价多30元,用880元购买A型号手办的数量是用290元购买B型号钥匙扣数量的2倍.
(1)(4分)求A,B两种型号纪念品的单价分别是多少元?
(2)(4分)若计划购买A,B两种型号的纪念品共100个,且所花费用不超过6800元,求最多能购买多少个A型号的纪念品?
22.(10分)某商店3月份购进一批T恤衫,进价合计12万元,因畅销,商店又于4月份购进一批同品牌T恤衫,进价合计15万元,数量是3月份的1.2倍,但每件进价涨了5元.
(1)(5分)3月份购进的T恤衫的单价是多少 4月份购进了多少件T恤衫
(2)(5分)这两批T恤衫开始都以每件180元出售,结果4月份后期出现滞销,还有一半的T恤衫没有售出,于是5月份商店便以定价的n折开始销售(n是正整数,且1≤n≤9),结果第二批T恤衫共盈利800m元(m为正整数).求m,n的值.
23.(10分)如图,在等边△ABC中,AB=6cm,动点P从点A出发以1cm/s的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.
(1)当t为何值时,△BPQ为直角三角形;
(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;
(3)求DE的长.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】
12.【答案】
13.【答案】6或7
14.【答案】6
15.【答案】
16.【答案】16
17.【答案】
18.【答案】9.
19.【答案】(1)
(2)1
20.【答案】解:设这个正多边形的边数为n,则根据题意,得:(n﹣2)×180°+360°=900°,
解得n=5, ;
答:这个多边形是正五边形,它每个内角的度数为108°.
21.【答案】(1)A型号的冰墩墩手办的单价为88元,B型号的冰墩墩钥匙扣的单价为58元
(2)33个
22.【答案】(1)解:设3月份购进的T恤衫的单价是x元,则4月份购进的T恤衫的单价是(x+5)元,
根据题意得:,
解得x=120,
经检验:x=120是原分式方程的解,
∴=1200件,
∴3月份购进的T恤衫的单价是120元,4月份购进了1200件T恤衫;
(2)解:4月份购进的T恤衫的单价为120+5=125元,
∴1200××(180-125)+1200××(180×-125)=800m,
整理得27n=2m+105,
∵m、n均为正整数,且1≤n≤9,
∴或或.
23.【答案】(1)2;(2)存在,t=3;(3)3cm
同课章节目录
