5.2 视图 练习（含答案）

中小学教育资源及组卷应用平台
2 第1课时 认识几何体的三种视图
知识点1 简单几何体的三种视图
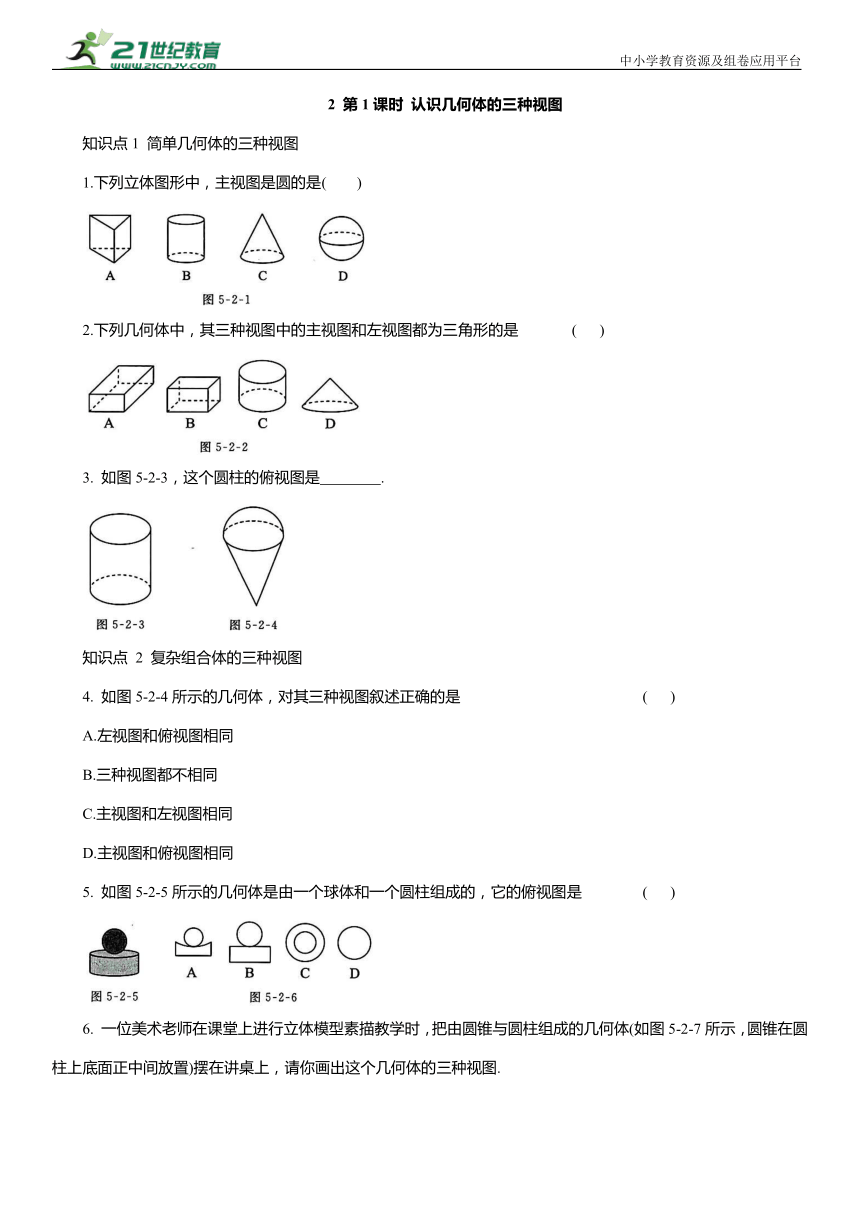
1.下列立体图形中，主视图是圆的是( )
2.下列几何体中，其三种视图中的主视图和左视图都为三角形的是 ( )
3. 如图5-2-3，这个圆柱的俯视图是 .
知识点 2 复杂组合体的三种视图
4. 如图5-2-4所示的几何体，对其三种视图叙述正确的是 ( )
A.左视图和俯视图相同
B.三种视图都不相同
C.主视图和左视图相同
D.主视图和俯视图相同
5. 如图5-2-5所示的几何体是由一个球体和一个圆柱组成的，它的俯视图是 ( )
6. 一位美术老师在课堂上进行立体模型素描教学时，把由圆锥与圆柱组成的几何体(如图5-2-7所示，圆锥在圆柱上底面正中间放置)摆在讲桌上，请你画出这个几何体的三种视图.
7. 将如图 5-2-8 所示的图形绕 AB所在的直线旋转一周，所得几何体的俯视图为 ( )
8. 如图5-2-10,空心卷筒纸的高度为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1：4的三种视图中，求主视图的面积.
第2课时 直棱柱的三种视图
知识点 1 认识直棱柱的三种视图
1. 如图5-2-11 所示的三棱柱的主视图是( )
2. 一个由长方体截去一部分后得到的几何体如图5-2-13水平放置，其俯视图是( )
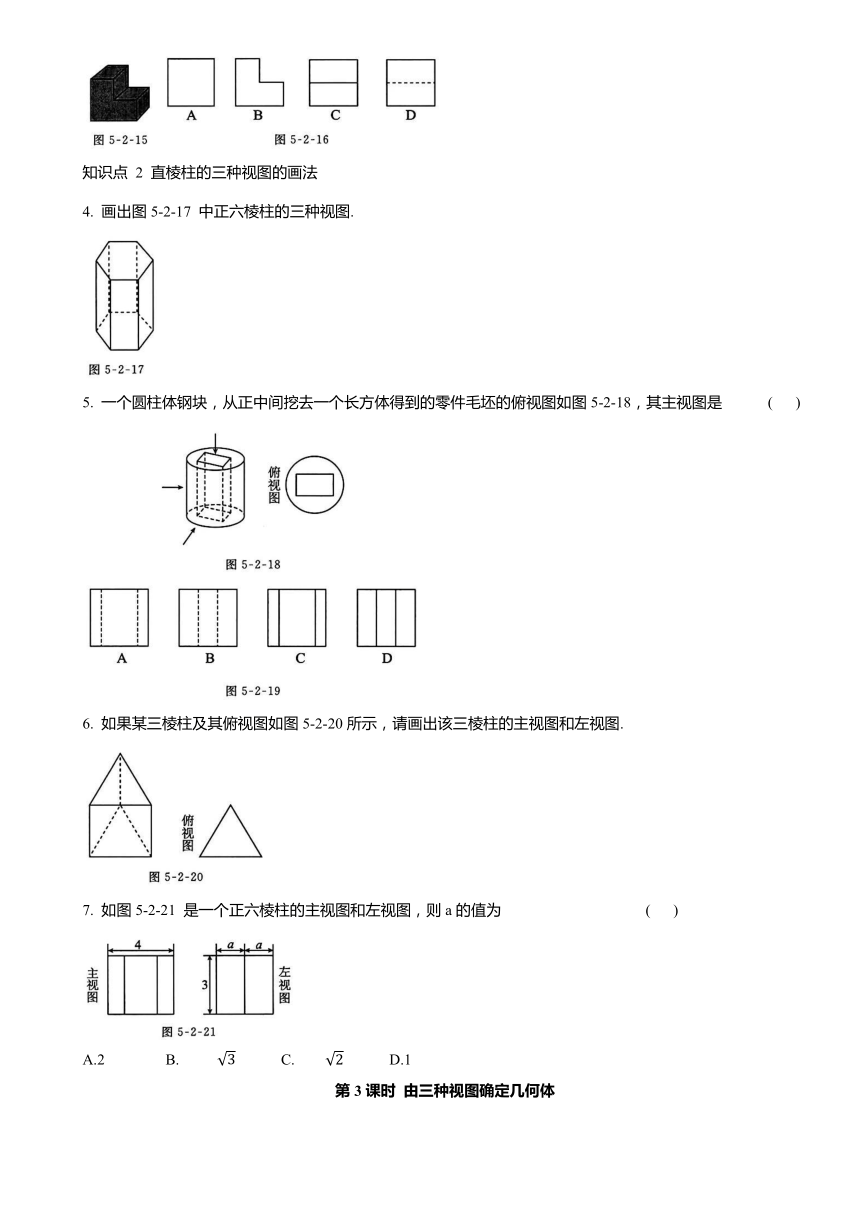
3. 一个正方体截去四分之一，得到如图5-2-15 所示的几何体，其左视图是 ( )
知识点 2 直棱柱的三种视图的画法
4. 画出图5-2-17 中正六棱柱的三种视图.
5. 一个圆柱体钢块，从正中间挖去一个长方体得到的零件毛坯的俯视图如图5-2-18，其主视图是 ( )
6. 如果某三棱柱及其俯视图如图5-2-20所示，请画出该三棱柱的主视图和左视图.
7. 如图5-2-21 是一个正六棱柱的主视图和左视图，则a的值为 ( )
A.2 B. C. D.1
第3课时 由三种视图确定几何体
知识点 1 由三种视图描述几何体
1.已知某几何体的三种视图如图5-2-22所示，则该几何体可能是 ( )
2. 如图5-2-24，根据三种视图，这个立体图形的名称是 ( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥知识点 2 画简单组合体的三种视图
3. 如图5-2-25 所示的几何体的俯视图可能是 ( )
4. 画出图5-2-27中立体图形的三种视图.
5. 某几何体的三种视图如图5-2-28所示，该几何体是 ( )
6. 如图5-2-30是实心零件的两种视图，求该零件的表面积.(结果保留π)
2 第1课时 认识几何体的三种视图
1. D 2. D
3. 圆 4. C
5. C [解析] 根据题意可得球体的俯视图是一个圆，圆柱的俯视图也是一个圆，且圆柱的底面圆的半径大于球体的半径，所以其俯视图如图.
故C选项符合题意.
故选 C.
6. 解：如图所示.
7. B [解析] 将该图形绕 AB 所在的直线旋转一周后得到由一个圆锥、一个圆柱组合而成的几何体，其俯视图是外面一个实线的大圆(包括圆心)，里面一个虚线的小圆.
故选 B.
8. 解:
∴3×2.5=7.5(cm ),
∴其主视图的面积是7.5 cm .
第2课时 直棱柱的三种视图
1. C 2. A 3. D
4. 解:如图.
5. A [解析] 从正面看，看不到中间挖去的长方体的侧棱，应为虚线.
6. 解：如图所示.
7. B
第3课时 由三种视图确定几何体
1. D
2. A [解析] 根据三种视图可以得出这个立体图形是三棱柱.故选 A.
3. C
4. 解：如图所示.
5. A
6. 解：由两种视图可得该零件为圆柱和长方体的组合体，所以该零件的表面积=2π×1×3+3×3×2+3×4×4=(6π+66)cm .