4.8 图形的位似练习（含答案）

中小学教育资源及组卷应用平台
8 第 1 课时 位似图形
知识点 1 位似图形的相关概念
1. 下列各选项的两个图形中，不是位似图形的是( )
2. 图4-8-2中的两个四边形是位似图形，位似中心是 ( )
A.点 M B.点 N C.点O D.点 P
知识点 2 位似图形的性质
3. 如图4-8-3,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C'，以下说法中错误的是 ( )
A.△ABC∽△A'B'C'
B. C,O,C'三点在同一直线上
D. AB∥A'B'
4. 如图4-8-4,四边形 ABCD 与四边形EFGH位似，其位似中心为点O，且 则
知识点 3 画位似图形
5.如图4-8-5,已知四边形 ABCD,以点O为位似中心画一个四边形A'B'C'D'，使四边形A'B'C'D'与四边形 ABCD 位似,且相似比为1: 2.
6.如图 4-8-6,△ABC 和△DEF 是以点O为位似中心的位似图形,相似 比为 2 : 3,则△ABC 和△DEF 的面积比是 .
7. 如图4-8-7,△ABC 与△A'B'C'是位似图形,点A,B,A',B',O共线,点O为位似中心.
(1)AC与A'C'平行吗 为什么
(2)若 AB=2A'B',OC'=5,则 CC'的长为
第 2课时 平面直角坐标系中的位似变换
知识点 1 已知位似图形求位似中心
1.在方格图中，以格点为顶点的三角形叫做格点三角形.在如图4-8-8所示的平面直角坐标系中，格点三角形 ABC，三角形DEF成位似关系，则位似中心的坐标为 ( )
A.(-1,0) B.(0,0)
C.(0,1) D.(1,0)
知识点 2 位似变换的坐标变化
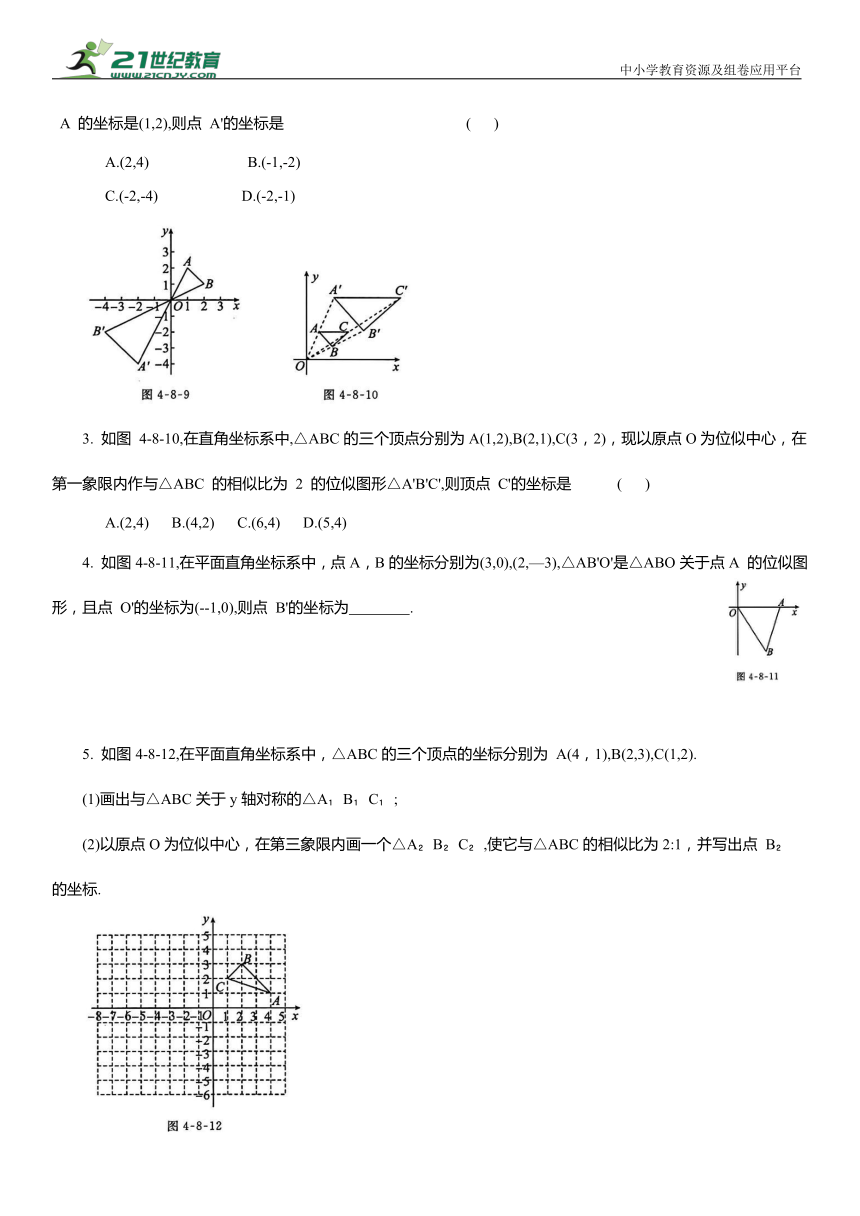
2. 如图4-8-9，在平面直角坐标系中，以原点O为位似中心，将△ABO扩大到原来的2倍，得到△A'B'O.若点 A 的坐标是(1,2),则点 A'的坐标是 ( )
A.(2,4) B.(-1,-2)
C.(-2,-4) D.(-2,-1)
3. 如图 4-8-10,在直角坐标系中,△ABC的三个顶点分别为A(1,2),B(2,1),C(3，2)，现以原点O为位似中心，在第一象限内作与△ABC 的相似比为 2 的位似图形△A'B'C',则顶点 C'的坐标是 ( )
A.(2,4) B.(4,2) C.(6,4) D.(5,4)
4. 如图4-8-11,在平面直角坐标系中，点A，B的坐标分别为(3,0),(2,—3),△AB'O'是△ABO关于点A 的位似图形，且点 O'的坐标为(--1,0),则点 B'的坐标为 .
5. 如图4-8-12,在平面直角坐标系中，△ABC的三个顶点的坐标分别为 A(4，1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A B C ;
(2)以原点O为位似中心，在第三象限内画一个△A B C ,使它与△ABC的相似比为2:1，并写出点 B 的坐标.
知识点 3 平面直角坐标系中的位似变换的应用
6.如图4-8-13,在平 面 直 角 坐 标 系 中，将△OAB 以原点O为位似中心放大后得到△OCD，若点B(0,1),D(0,3),则△OAB与△OCD 的相似比是
A.2:1 B.1:2 C.3:1 D.1:3
7. 如图 4-8-14,在平面直角坐标系中，四边形OABC 的顶点坐标分别是O(0，0),A(1,0),B(2,3),C(--1,2),若四边形OA'B'C'与四边形 OABC 关于原点 O位似,且四边形OA'B'C'的面积是四边形OABC 面积的 4 倍，则第一象限内点 B'的坐标为
8.如图4-8-15,在平面直角坐标系中,△OAB 与△OCD 位似,位似中心是原点 O.若点 A(4,0),C(2,0),则△OAB 与△OCD 周长的比值是 .
9. 如图4-8-16,在平面直角坐标系中,正方形 AB-CD与正方形 BEFG 是以原点O 为位似中心的位似图形，且相似比为 ,点 A,B,E在x轴上.若正方形 BEFG的边长为6，则点 C 的坐标为 ( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
10. 如图4-8-17,△AOB 三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以点O为位似中心，相似比为 ,将△AOB缩小,则点B的对应点 B'的坐标是 .
11. 如 图 4-8-18, 正方形 OABC 和正方形DEFG 是位似图形,点 B 的坐标为(-1,1),点 F 的坐标为(4，2)，且位似中心在这两个图形 的 同 侧，则位 似 中 心 的 坐 标 为
12. 已知：如图4-8-19，在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC三个顶点的坐标分别为A(0,-3),B(3,-2),C(2,-4).
(1)画出△ABC向上平移6个单位长度得到的△A B C ;
(2)以点 C 为位似中心，在网格中画出△A B C ,使△A B C 与△ABC 位似,且△A B C 与△ABC的相似比为2:1;
(3)求△A B C 与△A B C 的面积比.
1. C 2. D 3. C
4. [解析]
∵四边形 ABCD 与四边形EFGH 位似,
∴EH∥AD,∴易得△OEH∽△OAD,
故答案为
5. 解：答案不唯一，如图，画法如下：
(1)过点O分别作射线OA,OB,OC,OD;
(2)分别在射线OA,OB,OC,OD上取点A',B',C',D',使得
(3)顺次连接A'B',B'C',C'D',D'A',得到所要画的四边形A'B'C'D'.
6. 4:9
7. 解:(1)AC∥A'C'.理由如下:
∵△ABC与△A'B'C'是位似图形,
∴△ABC∽△A'B'C'.
∴∠A=∠C'A'B'.
∴AC∥A'C'.
(2)5 [解析] ∵△ABC与△A'B'C'是位似图形，点O为位似中心，
故答案为5.
第2课时 平面直角坐标系中的位似变换
1. A 2. C 3. C
5. 解:(1)如图,△A B C 为所作.
(2)如图,△A B C 为所作,点 B 的坐标为(--4,-6).
6. D [解析] ∵B(0,1),D(0,3),
∴OB=1,OD=3.
∵△OAB 以原点 O 为位似中心放大后得到△OCD,
∴△OAB 与△OCD 的相似比是 OB : OD=1:3.
故选 D.
7. (4,6) 8. 2 9. A
10. (2,4)或(-2,-4) [解析] 如图.
∵△OAB∽△OA'B',相似比为3:2,B(3,6),∴B'(2,4).根据对称性可知,当△OA"B"在第三象限时,B"(-2,-4),∴满足条件的点 B'的坐标为(2,4)或(-2,-4).
故答案为(2,4)或(-2,-4).
11. (-4,0) [解析] 如图,过点 B,G作直线交x轴于点 M，则点 M 即为位似中心.
∵点 B 的坐标为(-1,1),点 F 的坐标为(4,2),
∴AB=1,GD=2,AD=1+2=3.
∵AB∥GD,
∴易得△MAB∽△MDG,
∴MA=3,则OM=MA+OA=4,
∴M(-4,0).
12. 解:(1)如图所示,△A B C 即为所求.
(2)如图所示,△A B C 即为所求.
(3)∵△A B C 与△ABC 的相似比为 2 : 1,△ABC向上平移6个单位长度得到△A B C ,