2.3 第2课时 公式法的实际应用 练习(含答案)
文档属性
| 名称 | 2.3 第2课时 公式法的实际应用 练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第2课时 公式法的实际应用
知识点 实际生活中的应用
1. 用一条长 40 cm的绳子围成一个面积为64 cm 的矩形.设矩形的长为x cm,则可列方程为 ( )
A. x(20+x)=64 B. x(20-x)=64
C. x(40+x)=64 D. x(40-x)=64
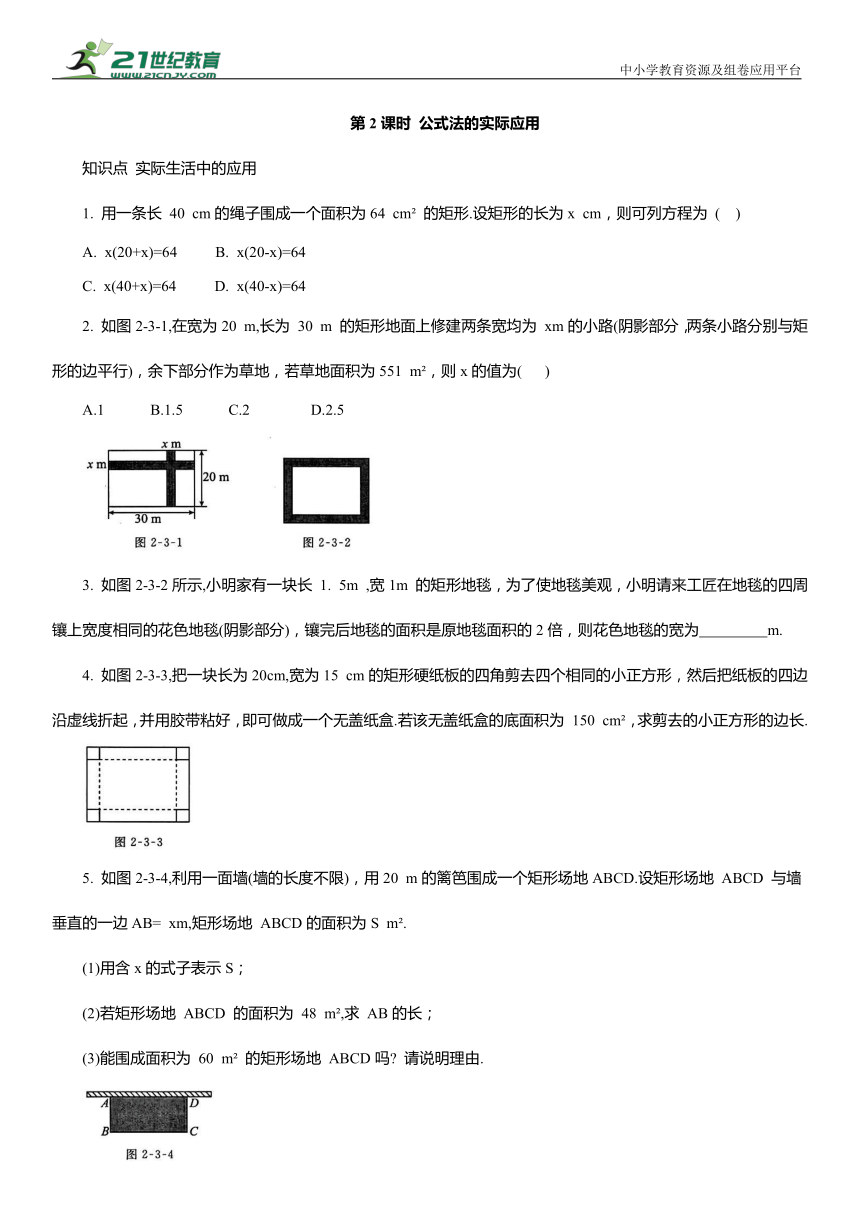
2. 如图2-3-1,在宽为20 m,长为 30 m 的矩形地面上修建两条宽均为 xm的小路(阴影部分,两条小路分别与矩形的边平行),余下部分作为草地,若草地面积为551 m ,则x的值为( )
A.1 B.1.5 C.2 D.2.5
3. 如图2-3-2所示,小明家有一块长 1. 5m ,宽1m 的矩形地毯,为了使地毯美观,小明请来工匠在地毯的四周镶上宽度相同的花色地毯(阴影部分),镶完后地毯的面积是原地毯面积的2倍,则花色地毯的宽为 m.
4. 如图2-3-3,把一块长为20cm,宽为15 cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为 150 cm ,求剪去的小正方形的边长.
5. 如图2-3-4,利用一面墙(墙的长度不限),用20 m的篱笆围成一个矩形场地ABCD.设矩形场地 ABCD 与墙垂直的一边AB= xm,矩形场地 ABCD的面积为S m .
(1)用含x的式子表示S;
(2)若矩形场地 ABCD 的面积为 48 m ,求 AB的长;
(3)能围成面积为 60 m 的矩形场地 ABCD吗 请说明理由.
6. 如 图 2-3-5, 在 △ABC中,∠ACB=90°,BC=a,AC=b.以点 B 为圆心,BC的长为半径画弧,交线段AB于点D,以点 A 为圆心,AD 的长为半径画弧,交线段AC于点E.下列哪条线段的长是关于x的方程 的一个根 ( )
A.线段 BC的长 B.线段AD 的长
C.线段EC的长 D.线段 AC 的长
7. 某新建火车站站前广场绿化工程中有一块长为20 米,宽为12 米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为112 平方米,两块绿地之间及周边留有宽度相等的人行通道(如图 2-3-6所示),则人行通道的宽是 米.
8. 在一块长16 m、宽 12 m 的矩形草坪上,要修建如图 2-3-7所示的两条宽均为 x m 的甬路,并使甬路所占面积为原来矩形草坪面积的一半,求甬路的宽.
9. 如图2-3-8,学校准备在围墙边用栅栏围成一个矩形场地 ABCD(靠墙一面不用栅栏),用于修建自行车棚,若所用栅栏的总长度为34米,墙的最大可用长度为18 米,为了出入方便,在垂直于墙的一边留了一个 2米宽的门(门用其他材料),设栅栏AB的长为x米,解答下列问题:
(1)BC= 米;(用含x的代数式表示)
(2)若围成的自行车棚 ABCD 的面积为154平方米,求栅栏 BC的长;
(3)围成的自行车棚ABCD 的面积能为200平方米吗 请说明理由.
10. 如图2-3-9,在△ABC中,∠B=90°,AB=12 cm,BC=16 cm.点 P 从点 A开始沿AB 边向点B 以1 cm/s的速度移动,点 Q 从点 B 开始沿 BC 边向点 C 以 2cm /s的速度移动.如果点 P,Q分别从点A,B同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为t s(t>0).
(1)当t= 时,△PBQ 的面积等于35 cm ;
(2)当t= 时,PQ的长度等于8 cm;
(3)若点 P,Q的速度保持不变,点P 在到达点B 后返回点A,点Q 在到达点C 后返回点B,一个点停止,另一个点也随之停止.当t为何值时,△PCQ的面积等于 32 cm
1. B
2. A [解析] 根据题意,得(30-x)(20-x)=551,化简,得 解得 因为当x=49时,20-x=-29<0,所以x的值为1.故选 A.
3. 0.25 [解析] 设花色地毯的宽为 xm,则(1.5+2x)(1+2x)=1.5×1×2,
解这个方程,得 (舍去),所以花色地毯的宽为0.25 m.
4. 解:设剪去的小正方形的边长是 x cm,则该无盖纸盒底面的长为(20-2x) cm,宽为(15-2x) cm.
根据题意,得(20-2x)(15-2x)=150,
整理,得
解得x =15(舍去),.
故剪去的小正方形的边长是2.5cm.
5. 解:(1)S=x(20-2x).
(2)依题意,得x(20-2x)=48,解得 故AB的长为4m 或6 m.
(3)不能.理由:假设能围成面积为60 m |的矩形场地 ABCD.
依题意,得x(20-2x)=60,
即
∴方程无实数解.
故不能围成面积为60 m 的矩形场地 ABCD.
6. B [解析] 由勾股定理,得
则
解方程 得
∴线段 AD的长是关于x的方程 的一个根.故选 B.
7. 2 [解析] 设人行通道的宽是x米,则两块矩形绿地可合成长为(20-3x)米,宽为(12--2x)米的矩形.
根据题意,得((20-3x)(12-2x)=112,解得
∵当 时,20-3x=--12<0,不符合题意,舍去,∴x=2.
故答案为2.
8. 解:设甬路的宽为 xm.
根据题意可列方程为 16×12,解得.
当x=24时,16-x=16-24=--8<0,不符合题意,舍去.
故甬路的宽为4m .
9. 解:(1)依题意得 AB+BC+CD-2=34,AB=CD=x,
∴BC=34+2-2x=(36-2x)米.
故答案为(36-2x).
(2)根据题意,可列方程为x(36-2x)=154,解得
当x=7时,36-2x=22>18,不合题意,舍去.
当x=11时,36-2x=14<18,符合题意,
∴栅栏 BC的长为14 米.
(3)不能.理由如下:
依题意得x(36-2x)=200,
整理得
,
∴方程没有实数根,
∴自行车棚ABCD的面积不能为200平方米.
10. 解:(1)由题意,得 BP=AB-AP=12-t,BQ=2t,
根据三角形的面积公式,得 即
整理,得 解得
故当 t 的值为 5 或7 时,△PBQ 的面积等于35 cm .故答案为5 或7.
根据勾股定理,得 整理,得 解得 故当t的值为 或4时,PQ的长度等于8 故答案为 或4.
(3)①当0②当8③当12解得 (舍去),
综上所述,当t的值为4 或16 时,△PCQ的面积等于 32 cm .
第2课时 公式法的实际应用
知识点 实际生活中的应用
1. 用一条长 40 cm的绳子围成一个面积为64 cm 的矩形.设矩形的长为x cm,则可列方程为 ( )
A. x(20+x)=64 B. x(20-x)=64
C. x(40+x)=64 D. x(40-x)=64
2. 如图2-3-1,在宽为20 m,长为 30 m 的矩形地面上修建两条宽均为 xm的小路(阴影部分,两条小路分别与矩形的边平行),余下部分作为草地,若草地面积为551 m ,则x的值为( )
A.1 B.1.5 C.2 D.2.5
3. 如图2-3-2所示,小明家有一块长 1. 5m ,宽1m 的矩形地毯,为了使地毯美观,小明请来工匠在地毯的四周镶上宽度相同的花色地毯(阴影部分),镶完后地毯的面积是原地毯面积的2倍,则花色地毯的宽为 m.
4. 如图2-3-3,把一块长为20cm,宽为15 cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为 150 cm ,求剪去的小正方形的边长.
5. 如图2-3-4,利用一面墙(墙的长度不限),用20 m的篱笆围成一个矩形场地ABCD.设矩形场地 ABCD 与墙垂直的一边AB= xm,矩形场地 ABCD的面积为S m .
(1)用含x的式子表示S;
(2)若矩形场地 ABCD 的面积为 48 m ,求 AB的长;
(3)能围成面积为 60 m 的矩形场地 ABCD吗 请说明理由.
6. 如 图 2-3-5, 在 △ABC中,∠ACB=90°,BC=a,AC=b.以点 B 为圆心,BC的长为半径画弧,交线段AB于点D,以点 A 为圆心,AD 的长为半径画弧,交线段AC于点E.下列哪条线段的长是关于x的方程 的一个根 ( )
A.线段 BC的长 B.线段AD 的长
C.线段EC的长 D.线段 AC 的长
7. 某新建火车站站前广场绿化工程中有一块长为20 米,宽为12 米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为112 平方米,两块绿地之间及周边留有宽度相等的人行通道(如图 2-3-6所示),则人行通道的宽是 米.
8. 在一块长16 m、宽 12 m 的矩形草坪上,要修建如图 2-3-7所示的两条宽均为 x m 的甬路,并使甬路所占面积为原来矩形草坪面积的一半,求甬路的宽.
9. 如图2-3-8,学校准备在围墙边用栅栏围成一个矩形场地 ABCD(靠墙一面不用栅栏),用于修建自行车棚,若所用栅栏的总长度为34米,墙的最大可用长度为18 米,为了出入方便,在垂直于墙的一边留了一个 2米宽的门(门用其他材料),设栅栏AB的长为x米,解答下列问题:
(1)BC= 米;(用含x的代数式表示)
(2)若围成的自行车棚 ABCD 的面积为154平方米,求栅栏 BC的长;
(3)围成的自行车棚ABCD 的面积能为200平方米吗 请说明理由.
10. 如图2-3-9,在△ABC中,∠B=90°,AB=12 cm,BC=16 cm.点 P 从点 A开始沿AB 边向点B 以1 cm/s的速度移动,点 Q 从点 B 开始沿 BC 边向点 C 以 2cm /s的速度移动.如果点 P,Q分别从点A,B同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为t s(t>0).
(1)当t= 时,△PBQ 的面积等于35 cm ;
(2)当t= 时,PQ的长度等于8 cm;
(3)若点 P,Q的速度保持不变,点P 在到达点B 后返回点A,点Q 在到达点C 后返回点B,一个点停止,另一个点也随之停止.当t为何值时,△PCQ的面积等于 32 cm
1. B
2. A [解析] 根据题意,得(30-x)(20-x)=551,化简,得 解得 因为当x=49时,20-x=-29<0,所以x的值为1.故选 A.
3. 0.25 [解析] 设花色地毯的宽为 xm,则(1.5+2x)(1+2x)=1.5×1×2,
解这个方程,得 (舍去),所以花色地毯的宽为0.25 m.
4. 解:设剪去的小正方形的边长是 x cm,则该无盖纸盒底面的长为(20-2x) cm,宽为(15-2x) cm.
根据题意,得(20-2x)(15-2x)=150,
整理,得
解得x =15(舍去),.
故剪去的小正方形的边长是2.5cm.
5. 解:(1)S=x(20-2x).
(2)依题意,得x(20-2x)=48,解得 故AB的长为4m 或6 m.
(3)不能.理由:假设能围成面积为60 m |的矩形场地 ABCD.
依题意,得x(20-2x)=60,
即
∴方程无实数解.
故不能围成面积为60 m 的矩形场地 ABCD.
6. B [解析] 由勾股定理,得
则
解方程 得
∴线段 AD的长是关于x的方程 的一个根.故选 B.
7. 2 [解析] 设人行通道的宽是x米,则两块矩形绿地可合成长为(20-3x)米,宽为(12--2x)米的矩形.
根据题意,得((20-3x)(12-2x)=112,解得
∵当 时,20-3x=--12<0,不符合题意,舍去,∴x=2.
故答案为2.
8. 解:设甬路的宽为 xm.
根据题意可列方程为 16×12,解得.
当x=24时,16-x=16-24=--8<0,不符合题意,舍去.
故甬路的宽为4m .
9. 解:(1)依题意得 AB+BC+CD-2=34,AB=CD=x,
∴BC=34+2-2x=(36-2x)米.
故答案为(36-2x).
(2)根据题意,可列方程为x(36-2x)=154,解得
当x=7时,36-2x=22>18,不合题意,舍去.
当x=11时,36-2x=14<18,符合题意,
∴栅栏 BC的长为14 米.
(3)不能.理由如下:
依题意得x(36-2x)=200,
整理得
,
∴方程没有实数根,
∴自行车棚ABCD的面积不能为200平方米.
10. 解:(1)由题意,得 BP=AB-AP=12-t,BQ=2t,
根据三角形的面积公式,得 即
整理,得 解得
故当 t 的值为 5 或7 时,△PBQ 的面积等于35 cm .故答案为5 或7.
根据勾股定理,得 整理,得 解得 故当t的值为 或4时,PQ的长度等于8 故答案为 或4.
(3)①当0
综上所述,当t的值为4 或16 时,△PCQ的面积等于 32 cm .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
