1.1 菱形的性质和判定 第2课时 菱形的判定 同步练习(含答案)
文档属性
| 名称 | 1.1 菱形的性质和判定 第2课时 菱形的判定 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 236.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 16:57:37 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.1菱形的性质和判定
第2课时菱形的判定
知识点 1 根据菱形的定义进行菱形的判定
1. 如图1-1-15,要使 ABCD成为菱形,则需添加的一个条件可以是 ( )
A. AC=AD B. BA=BC
C.∠ABC=90° D. AC=BD
2. 如图1-1-16,在 ABCD中,AB=9 cm,BC=4 cm,将 CB 沿 BA 方向平移得到 EF(点 F在边AB 上),则当 BF= cm时,四边形 DAFE 是菱形,依据是 .
3. 如图1-1-17,在△ABC中,AD 平分∠BAC,DE∥AC交AB 于点E,DF∥AB交AC 于点F.求证:四边形AEDF 是菱形.
知识点 2 根据对角线进行菱形的判定
4. 如图 1-1-18,已知 ABCD,AC,BD交于点O,绕点O旋转对角线 AC,∠AOD=α,当α= °时,四边形 ABCD 是菱形,依据是
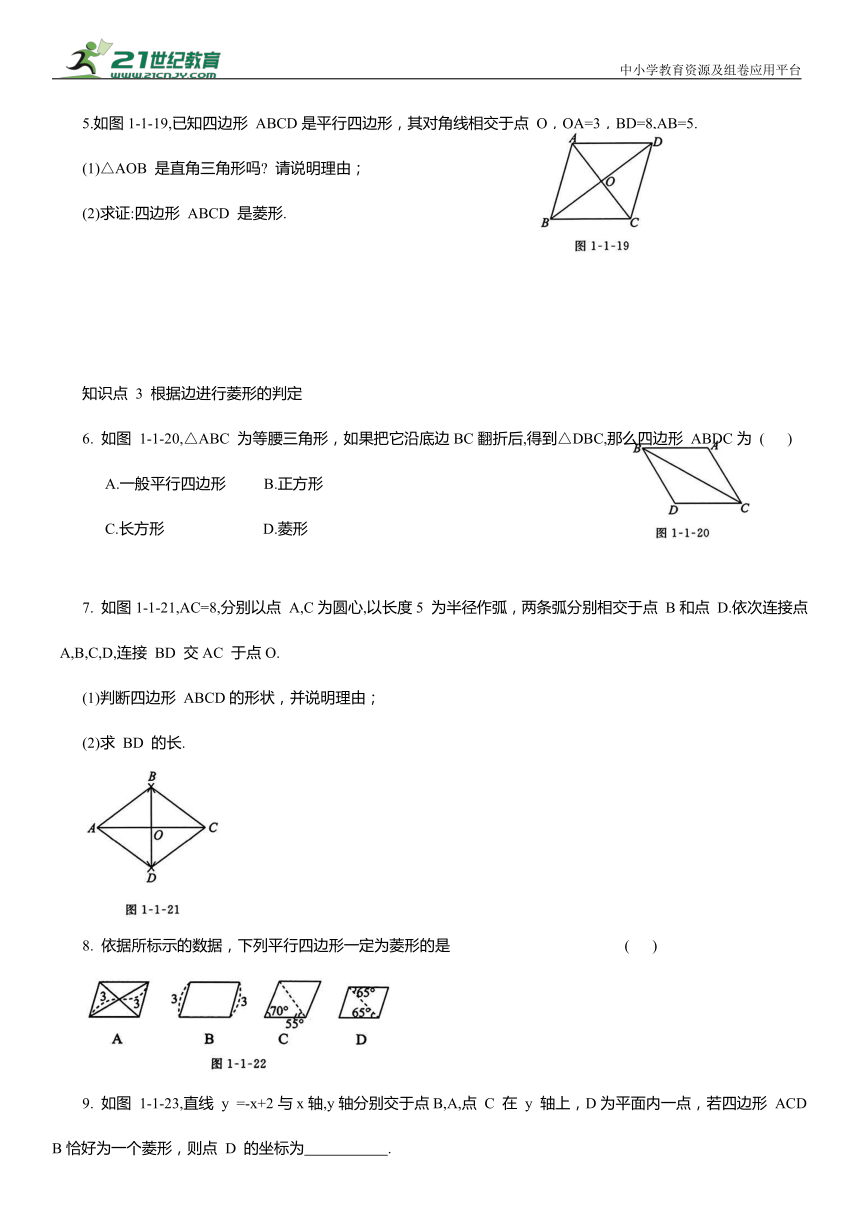
5.如图1-1-19,已知四边形 ABCD是平行四边形,其对角线相交于点 O,OA=3,BD=8,AB=5.
(1)△AOB 是直角三角形吗 请说明理由;
(2)求证:四边形 ABCD 是菱形.
知识点 3 根据边进行菱形的判定
6. 如图 1-1-20,△ABC 为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形 ABDC为 ( )
A.一般平行四边形 B.正方形
C.长方形 D.菱形
7. 如图1-1-21,AC=8,分别以点 A,C为圆心,以长度5 为半径作弧,两条弧分别相交于点 B和点 D.依次连接点 A,B,C,D,连接 BD 交AC 于点O.
(1)判断四边形 ABCD的形状,并说明理由;
(2)求 BD 的长.
8. 依据所标示的数据,下列平行四边形一定为菱形的是 ( )
9. 如图 1-1-23,直线 y =-x+2与x轴,y轴分别交于点B,A,点 C 在 y 轴上,D为平面内一点,若四边形 ACDB恰好为一个菱形,则点 D 的坐标为 .
10.如图1-1-24,四边形 ABCD 是平行四边形,BM∥DN,且分别交对角线 AC于点 M,N,连接MD,BN.
(1)求证:∠DMN=∠BNM;
(2)若∠BAC=∠DAC.求证:四边形 BMDN是菱形.
11. 某校九年级学习小组在探究学习过程中,用两块完全相同且含 60°角的三角尺ABC与三角尺 AEF 按图1-1-25①所示方式放置,点 F 在 AC 上,点 B 在 AE 上,∠A=90°,∠ABC=∠AFE=60°.现将三角尺 AEF 绕点A 按逆时针方向旋转角α(0°<α<90°),如图②,AE 与 BC 交于点 M,AC与EF 交于点N,BC 与EF 交于点 P.
(1)求证:AM=AN;
(2)当α=30°时,判断四边形 ABPF 的形状,并说明理由.
1. B [解析] 有一组邻边相等的平行四边形是菱形.要使 ABCD成为菱形,则需添加的一个条件可以是 BA=BC.
故选 B.
2. 5 有一组邻边相等的平行四边形是菱形
3. 证明:∵AD平分∠BAC,
∴∠EAD=∠FAD.
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∴∠FAD=∠ADF,则AF=DF,
∴四边形 AEDF 是菱形.
4. 90 对角线互相垂直的平行四边形是菱形
5. 解:(1)△AOB是直角三角形.理由如下:
∵四边形 ABCD 是平行四边形,
∴△AOB是直角三角形.
(2)证明:由(1)可得△AOB 是直角三角形,∠AOB=90°,即AC⊥BD.
又∵四边形 ABCD 是平行四边形,∴四边形 ABCD 是菱形.
6. D
7. 解:(1)四边形 ABCD 为菱形.
理由:由作法得AB=AD=CB=CD=5,∴四边形 ABCD 为菱形.
(2)∵四边形ABCD为菱形,
在Rt△AOB中,( ∴BD=2OB=6.
8. C
9. (2,2 )或(
[解析] ∵直线y=-x+2与x轴,y轴分别交于点B,A,
∴A(0,2),B(2,0),
∴OA=OB=2,
∵四边形 ACDB 是菱形,
∴AC=CD=BD=AB=2
当点C在点A 上方时,过点 D 作DH⊥y轴于点 H.
∵AC∥BD,AC⊥x轴,
∴BD⊥x轴,
∴四边形 OBDH 是长方形,
当点C在点 A下方时,同理可得D(2,-2 ).
故答案为(2,2 )或(
10. 证明:(1)连接BD,交AC于点O,如图.
∵四边形ABCD 是平行四边形,
∴OB=OD.
∵BM∥DN,
∴∠MBO=∠NDO.
又∠BOM=∠DON,
∴△BOM≌△DON(ASA),
∴BM=DN,
则四边形 BMDN 为平行四边形,
∴BN∥DM,
∴∠DMN=∠BNM.
(2)∵四边形ABCD 是平行四边形,
∴BC∥AD,
∴∠BCA=∠DAC.
又∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC,
则四边形ABCD是菱形,
∴AC⊥BD,
∴MN⊥BD,
∴平行四边形 BMDN 是菱形.
11. 解:(1)证明: ∵∠MAB +∠EAC = 90°,∠NAF+∠EAC=90°,
∴∠MAB=∠NAF.
又∵AB=AF,∠ABC=∠AFE,
∴△ABM≌△AFN.∴AM=AN.
(2)当α=30°时,四边形ABPF 是菱形.
理由:∵α=30°,∠EAF=90°,
∴∠BAF=120°.
又∵∠ABC=∠AFE=60°,
∴AF∥BC,AB∥EF.
∴四边形ABPF 是平行四边形.
又∵AB=AF,∴□ABPF 是菱形.
1.1菱形的性质和判定
第2课时菱形的判定
知识点 1 根据菱形的定义进行菱形的判定
1. 如图1-1-15,要使 ABCD成为菱形,则需添加的一个条件可以是 ( )
A. AC=AD B. BA=BC
C.∠ABC=90° D. AC=BD
2. 如图1-1-16,在 ABCD中,AB=9 cm,BC=4 cm,将 CB 沿 BA 方向平移得到 EF(点 F在边AB 上),则当 BF= cm时,四边形 DAFE 是菱形,依据是 .
3. 如图1-1-17,在△ABC中,AD 平分∠BAC,DE∥AC交AB 于点E,DF∥AB交AC 于点F.求证:四边形AEDF 是菱形.
知识点 2 根据对角线进行菱形的判定
4. 如图 1-1-18,已知 ABCD,AC,BD交于点O,绕点O旋转对角线 AC,∠AOD=α,当α= °时,四边形 ABCD 是菱形,依据是
5.如图1-1-19,已知四边形 ABCD是平行四边形,其对角线相交于点 O,OA=3,BD=8,AB=5.
(1)△AOB 是直角三角形吗 请说明理由;
(2)求证:四边形 ABCD 是菱形.
知识点 3 根据边进行菱形的判定
6. 如图 1-1-20,△ABC 为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形 ABDC为 ( )
A.一般平行四边形 B.正方形
C.长方形 D.菱形
7. 如图1-1-21,AC=8,分别以点 A,C为圆心,以长度5 为半径作弧,两条弧分别相交于点 B和点 D.依次连接点 A,B,C,D,连接 BD 交AC 于点O.
(1)判断四边形 ABCD的形状,并说明理由;
(2)求 BD 的长.
8. 依据所标示的数据,下列平行四边形一定为菱形的是 ( )
9. 如图 1-1-23,直线 y =-x+2与x轴,y轴分别交于点B,A,点 C 在 y 轴上,D为平面内一点,若四边形 ACDB恰好为一个菱形,则点 D 的坐标为 .
10.如图1-1-24,四边形 ABCD 是平行四边形,BM∥DN,且分别交对角线 AC于点 M,N,连接MD,BN.
(1)求证:∠DMN=∠BNM;
(2)若∠BAC=∠DAC.求证:四边形 BMDN是菱形.
11. 某校九年级学习小组在探究学习过程中,用两块完全相同且含 60°角的三角尺ABC与三角尺 AEF 按图1-1-25①所示方式放置,点 F 在 AC 上,点 B 在 AE 上,∠A=90°,∠ABC=∠AFE=60°.现将三角尺 AEF 绕点A 按逆时针方向旋转角α(0°<α<90°),如图②,AE 与 BC 交于点 M,AC与EF 交于点N,BC 与EF 交于点 P.
(1)求证:AM=AN;
(2)当α=30°时,判断四边形 ABPF 的形状,并说明理由.
1. B [解析] 有一组邻边相等的平行四边形是菱形.要使 ABCD成为菱形,则需添加的一个条件可以是 BA=BC.
故选 B.
2. 5 有一组邻边相等的平行四边形是菱形
3. 证明:∵AD平分∠BAC,
∴∠EAD=∠FAD.
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∴∠FAD=∠ADF,则AF=DF,
∴四边形 AEDF 是菱形.
4. 90 对角线互相垂直的平行四边形是菱形
5. 解:(1)△AOB是直角三角形.理由如下:
∵四边形 ABCD 是平行四边形,
∴△AOB是直角三角形.
(2)证明:由(1)可得△AOB 是直角三角形,∠AOB=90°,即AC⊥BD.
又∵四边形 ABCD 是平行四边形,∴四边形 ABCD 是菱形.
6. D
7. 解:(1)四边形 ABCD 为菱形.
理由:由作法得AB=AD=CB=CD=5,∴四边形 ABCD 为菱形.
(2)∵四边形ABCD为菱形,
在Rt△AOB中,( ∴BD=2OB=6.
8. C
9. (2,2 )或(
[解析] ∵直线y=-x+2与x轴,y轴分别交于点B,A,
∴A(0,2),B(2,0),
∴OA=OB=2,
∵四边形 ACDB 是菱形,
∴AC=CD=BD=AB=2
当点C在点A 上方时,过点 D 作DH⊥y轴于点 H.
∵AC∥BD,AC⊥x轴,
∴BD⊥x轴,
∴四边形 OBDH 是长方形,
当点C在点 A下方时,同理可得D(2,-2 ).
故答案为(2,2 )或(
10. 证明:(1)连接BD,交AC于点O,如图.
∵四边形ABCD 是平行四边形,
∴OB=OD.
∵BM∥DN,
∴∠MBO=∠NDO.
又∠BOM=∠DON,
∴△BOM≌△DON(ASA),
∴BM=DN,
则四边形 BMDN 为平行四边形,
∴BN∥DM,
∴∠DMN=∠BNM.
(2)∵四边形ABCD 是平行四边形,
∴BC∥AD,
∴∠BCA=∠DAC.
又∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC,
则四边形ABCD是菱形,
∴AC⊥BD,
∴MN⊥BD,
∴平行四边形 BMDN 是菱形.
11. 解:(1)证明: ∵∠MAB +∠EAC = 90°,∠NAF+∠EAC=90°,
∴∠MAB=∠NAF.
又∵AB=AF,∠ABC=∠AFE,
∴△ABM≌△AFN.∴AM=AN.
(2)当α=30°时,四边形ABPF 是菱形.
理由:∵α=30°,∠EAF=90°,
∴∠BAF=120°.
又∵∠ABC=∠AFE=60°,
∴AF∥BC,AB∥EF.
∴四边形ABPF 是平行四边形.
又∵AB=AF,∴□ABPF 是菱形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
