北师大版六年级上册数学第十一周灵活应用单位“1”课件(共21张PPT)
文档属性
| 名称 | 北师大版六年级上册数学第十一周灵活应用单位“1”课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 07:58:03 | ||
图片预览








文档简介
(共21张PPT)
甲、乙工厂生产产品的数量比是2:3,单价的比为9:10,已知两个厂的总产值为640万元,两厂的产值各是多少万元?
640 × = 240 (万元)
甲厂产值:乙厂产值=(2×9):(3×10) = 3 : 5
甲厂产值:
640 × = 400(万元)
乙厂产值:
答:甲厂产值240万元,乙厂产值400万元。
复习:
甲、乙、丙三个数的平均数是120,三个数的比是1:2:3,这三个数分别是多少?
三个数的和=120×3= 360
甲:
360 × = 60 (万元)
乙:
360 × = 120 (万元)
丙:
360 × = 180 (万元)
思维训练课
灵活应用单位“1”
小学 / 数学 / 北师大版 / 六年级上册
把一个完整的量(比如一段路程、一项工程、一筐苹果、一本书、一段时间等)或一个数看做为一个整体或一个单位,可记为“1”。
知识链接:
确定单位“1”是解答分数、百分数应用题的关键,是分析数量关系的突破点。灵活选用单位“1”,往往能起到事半功倍的效果。
判断单位“1”。
知识链接:
1、 一种服装原现在卖105元,相当于原来售价的
2、仓库有一堆货物。第一次运走5吨,占全部货物的
3、五年级人数的与六年级人数相等。
4、妈妈带200元,买肉用去了
5、一根绳子长12米,正好是另一根绳子的
思路点拨:题中有一个隐含的条件“一半”,“一半”用分率表示就是,题中的两个分率对应的单位“1”是相同的,都是这桶油的总量。这样就可以找出第一天用的9千克所对应的分率:(1--)。应用“量率对应”的思想就可以求出单位“1”,也就是这桶油原来的总质量。
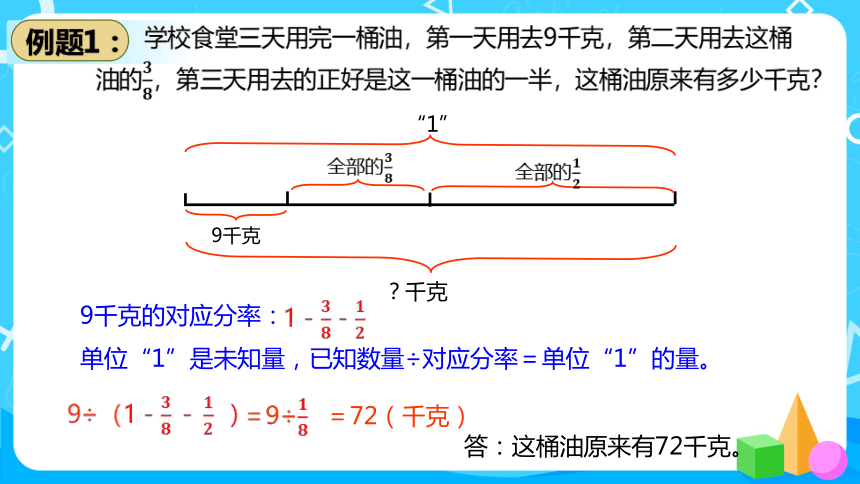
例题1:
学校食堂三天用完一桶油,第一天用去9千克,第二天用去这桶油的,第三天用去的正好是这一桶油的一半,这桶油原来有多少千克?
“一半”=
9千克的对应分率:1--
例题1:
“1”
全部的
9千克
?千克
单位“1”是未知量,已知数量÷对应分率=单位“1”的量。
9÷(1- )
=9÷
=72(千克)
答:这桶油原来有72千克。
学校食堂三天用完一桶油,第一天用去9千克,第二天用去这桶油的,第三天用去的正好是这一桶油的一半,这桶油原来有多少千克?
全部的
9千克的对应分率:
1--
练一练:
食堂职工三天用完一桶油,第一天用去5千克,第二天用去这桶油的,第三天用去的正好是这一桶油的一半,这桶油原来有多少千克?
5÷(1 )
=5÷
=5×4
=20(千克)
答:这桶油原来有20千克。
思路点拨:这道题的难点在于题中的单位“1”一直在变化:是以“中、高年级人数”为单位“1”,而是以“低,高年级人数”为单位“1”。遇到这类问题时,要找一个不变的量作为单位“1”,抓住不变量。
例题2:
开学时,学校统计学生人数时发现:低年级人数占中、高年级人数的,中年级人数占低、高年级人数的已知高年级有210人,这个学校一共有多少人?
全校人数是不变的,用全校人数作为单位“1”:
低年级人数占中、高年级人数的
低年级人数占全校人数的
中年级人数占低、高年级人数的
中年级人数占全校人数的
例题2:
开学时,学校总务处统计学生人数时发现:低年级人数占中、高年级人数的,中年级人数占低、高年级人数的已知高年级有210人,这个学校一共有多少人?
全校人数是不变的,用全校人数作为单位“1”:
低年级人数占中、高年级人数的
低年级人数占全校人数的
中年级人数占低、高年级人数的
中年级人数占全校人数的
高年级人数占全校人数的
1
210÷(1
=210÷
=735(人)
答:这个学校一共有735人。
练一练:
甲数是乙丙两数和的乙数是甲丙两数和的,丙数是25,
甲乙丙三个数的和是多少?
甲数是乙丙两数和的
甲数占总数的
乙数是甲丙两数和的
乙数占总数的
丙数占总数的
1
25÷
答:甲乙丙三个数的和是60。
思路点拨:这两个条件中都用甲筐做单位“1”,但是第一个“甲筐”和第二个“甲筐”数量变了,也就是单位“1”变了。
例题3:
有两筐梨,乙筐是甲筐的,从甲筐中取出5千克梨放入乙筐后,乙筐的梨是甲筐的,甲乙两筐梨原来各有多少千克?
思路点拨:由于题中两筐梨的总重量没有变,我们把两筐梨的总重量看作单位“1”,则原来甲筐的梨占总重量的,后来甲筐的梨占总重量的,所以5千克梨相当于总重量的=
例题3:
有两筐梨,乙筐是甲筐的,从甲筐中取出5千克梨放入乙筐后,乙筐的梨是甲筐的,甲乙两筐梨原来各有多少千克?
乙筐是甲筐的
甲筐占总量的=
乙筐是甲筐的
甲筐占总量的=
5÷(
=
答:甲筐原有50千克,乙筐原有30千克。
有两筐梨,乙筐是甲筐的,从甲筐中取出13千克梨放入乙筐后,乙筐的梨是甲筐的,甲乙两筐梨原来各有多少千克?
乙筐是甲筐的
甲筐占总量的=
乙筐是甲筐的
甲筐占总量的=
13÷(
=
答:甲筐原有48千克,乙筐原有12千克。
练一练:
思路点拨:两个分率对应的单位“1”不同,要找到40人的对应分率,用量率对应的方法可以求出单位“1”。
例题4:
参加六一儿童节联欢活动的少先队员中,女队员人数占全体少先队员的,男队员人数比女队员人数的多40人,女队员有多少人?
女队员人数占全体少先队员的,男队员人数比女队员人数的多40人
男队员人数比全体少先队员的×=多40人。
男队员人数占全体少先队员的1-=。
40人的对应分率:-
例题4:
参加六一儿童节联欢活动的少先队员中,女队员人数占全体少先队员的,男队员人数比女队员人数的多40人,女队员有多少人?
×=
1-=
-
=
=
答:女队员有480人。
学校买来一些皮球和足球,皮球占总数的,足球比皮球只数的少6只,学校买来皮球和足球各多少只?
×=
1-=
-
=
=
答:学校买来皮球54只,足球各36只。
练一练:
思路点拨:表面上看两个分率对应的单位“1”是相同的,但由于又买进20根长跳绳,题中“”与“”这两个分数的对应的单位“1”并不相同。根据短跳绳的根数没有变,我们把短跳绳的根数看作单位“1”。
例题5:
学校原有长跳绳的根数占长、短跳绳总数的,后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的,这所学校现有长、短跳绳共多少根?
原来的长跳绳根数占短跳绳的
买进20根长跳绳后,长跳绳根数占短跳绳的
20根长跳绳的对应分率:
例题5:
某学校原有长跳绳的根数占长、短跳绳总数的,后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的,这所学校现有长、短跳绳共多少根?
原来的长跳绳根数占短跳绳的
买进20根长跳绳后,长跳绳根数占短跳绳的
-
=
=
答:学校现有长跳绳35根,短跳绳25根。
学校原有篮球的数量占篮球和足球总数的,后来又买进12个篮球,这时篮球的数量占两种球总数的,这所学校现有篮球、足球共多少个?
原来的篮球占足球的
买进12个篮球后,篮球占足球的
-
=
=
答:学校现有篮球、足球共62个。
练一练:
练一练:
三个粮仓,甲仓库存粮120吨,乙仓库存的粮食占乙、丙两仓库和的丙仓存粮占甲、乙、丙三个仓库总和的,三个仓库共有存粮多少吨?
乙仓库占乙、丙两仓库和的
丙仓库占总数的
乙仓库占总数的:
乙仓库占丙仓的
120÷(1-
答:三个仓库共有存粮240吨。
甲仓库占丙仓的1-
总结:
这节课有什么收获?
甲、乙工厂生产产品的数量比是2:3,单价的比为9:10,已知两个厂的总产值为640万元,两厂的产值各是多少万元?
640 × = 240 (万元)
甲厂产值:乙厂产值=(2×9):(3×10) = 3 : 5
甲厂产值:
640 × = 400(万元)
乙厂产值:
答:甲厂产值240万元,乙厂产值400万元。
复习:
甲、乙、丙三个数的平均数是120,三个数的比是1:2:3,这三个数分别是多少?
三个数的和=120×3= 360
甲:
360 × = 60 (万元)
乙:
360 × = 120 (万元)
丙:
360 × = 180 (万元)
思维训练课
灵活应用单位“1”
小学 / 数学 / 北师大版 / 六年级上册
把一个完整的量(比如一段路程、一项工程、一筐苹果、一本书、一段时间等)或一个数看做为一个整体或一个单位,可记为“1”。
知识链接:
确定单位“1”是解答分数、百分数应用题的关键,是分析数量关系的突破点。灵活选用单位“1”,往往能起到事半功倍的效果。
判断单位“1”。
知识链接:
1、 一种服装原现在卖105元,相当于原来售价的
2、仓库有一堆货物。第一次运走5吨,占全部货物的
3、五年级人数的与六年级人数相等。
4、妈妈带200元,买肉用去了
5、一根绳子长12米,正好是另一根绳子的
思路点拨:题中有一个隐含的条件“一半”,“一半”用分率表示就是,题中的两个分率对应的单位“1”是相同的,都是这桶油的总量。这样就可以找出第一天用的9千克所对应的分率:(1--)。应用“量率对应”的思想就可以求出单位“1”,也就是这桶油原来的总质量。
例题1:
学校食堂三天用完一桶油,第一天用去9千克,第二天用去这桶油的,第三天用去的正好是这一桶油的一半,这桶油原来有多少千克?
“一半”=
9千克的对应分率:1--
例题1:
“1”
全部的
9千克
?千克
单位“1”是未知量,已知数量÷对应分率=单位“1”的量。
9÷(1- )
=9÷
=72(千克)
答:这桶油原来有72千克。
学校食堂三天用完一桶油,第一天用去9千克,第二天用去这桶油的,第三天用去的正好是这一桶油的一半,这桶油原来有多少千克?
全部的
9千克的对应分率:
1--
练一练:
食堂职工三天用完一桶油,第一天用去5千克,第二天用去这桶油的,第三天用去的正好是这一桶油的一半,这桶油原来有多少千克?
5÷(1 )
=5÷
=5×4
=20(千克)
答:这桶油原来有20千克。
思路点拨:这道题的难点在于题中的单位“1”一直在变化:是以“中、高年级人数”为单位“1”,而是以“低,高年级人数”为单位“1”。遇到这类问题时,要找一个不变的量作为单位“1”,抓住不变量。
例题2:
开学时,学校统计学生人数时发现:低年级人数占中、高年级人数的,中年级人数占低、高年级人数的已知高年级有210人,这个学校一共有多少人?
全校人数是不变的,用全校人数作为单位“1”:
低年级人数占中、高年级人数的
低年级人数占全校人数的
中年级人数占低、高年级人数的
中年级人数占全校人数的
例题2:
开学时,学校总务处统计学生人数时发现:低年级人数占中、高年级人数的,中年级人数占低、高年级人数的已知高年级有210人,这个学校一共有多少人?
全校人数是不变的,用全校人数作为单位“1”:
低年级人数占中、高年级人数的
低年级人数占全校人数的
中年级人数占低、高年级人数的
中年级人数占全校人数的
高年级人数占全校人数的
1
210÷(1
=210÷
=735(人)
答:这个学校一共有735人。
练一练:
甲数是乙丙两数和的乙数是甲丙两数和的,丙数是25,
甲乙丙三个数的和是多少?
甲数是乙丙两数和的
甲数占总数的
乙数是甲丙两数和的
乙数占总数的
丙数占总数的
1
25÷
答:甲乙丙三个数的和是60。
思路点拨:这两个条件中都用甲筐做单位“1”,但是第一个“甲筐”和第二个“甲筐”数量变了,也就是单位“1”变了。
例题3:
有两筐梨,乙筐是甲筐的,从甲筐中取出5千克梨放入乙筐后,乙筐的梨是甲筐的,甲乙两筐梨原来各有多少千克?
思路点拨:由于题中两筐梨的总重量没有变,我们把两筐梨的总重量看作单位“1”,则原来甲筐的梨占总重量的,后来甲筐的梨占总重量的,所以5千克梨相当于总重量的=
例题3:
有两筐梨,乙筐是甲筐的,从甲筐中取出5千克梨放入乙筐后,乙筐的梨是甲筐的,甲乙两筐梨原来各有多少千克?
乙筐是甲筐的
甲筐占总量的=
乙筐是甲筐的
甲筐占总量的=
5÷(
=
答:甲筐原有50千克,乙筐原有30千克。
有两筐梨,乙筐是甲筐的,从甲筐中取出13千克梨放入乙筐后,乙筐的梨是甲筐的,甲乙两筐梨原来各有多少千克?
乙筐是甲筐的
甲筐占总量的=
乙筐是甲筐的
甲筐占总量的=
13÷(
=
答:甲筐原有48千克,乙筐原有12千克。
练一练:
思路点拨:两个分率对应的单位“1”不同,要找到40人的对应分率,用量率对应的方法可以求出单位“1”。
例题4:
参加六一儿童节联欢活动的少先队员中,女队员人数占全体少先队员的,男队员人数比女队员人数的多40人,女队员有多少人?
女队员人数占全体少先队员的,男队员人数比女队员人数的多40人
男队员人数比全体少先队员的×=多40人。
男队员人数占全体少先队员的1-=。
40人的对应分率:-
例题4:
参加六一儿童节联欢活动的少先队员中,女队员人数占全体少先队员的,男队员人数比女队员人数的多40人,女队员有多少人?
×=
1-=
-
=
=
答:女队员有480人。
学校买来一些皮球和足球,皮球占总数的,足球比皮球只数的少6只,学校买来皮球和足球各多少只?
×=
1-=
-
=
=
答:学校买来皮球54只,足球各36只。
练一练:
思路点拨:表面上看两个分率对应的单位“1”是相同的,但由于又买进20根长跳绳,题中“”与“”这两个分数的对应的单位“1”并不相同。根据短跳绳的根数没有变,我们把短跳绳的根数看作单位“1”。
例题5:
学校原有长跳绳的根数占长、短跳绳总数的,后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的,这所学校现有长、短跳绳共多少根?
原来的长跳绳根数占短跳绳的
买进20根长跳绳后,长跳绳根数占短跳绳的
20根长跳绳的对应分率:
例题5:
某学校原有长跳绳的根数占长、短跳绳总数的,后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的,这所学校现有长、短跳绳共多少根?
原来的长跳绳根数占短跳绳的
买进20根长跳绳后,长跳绳根数占短跳绳的
-
=
=
答:学校现有长跳绳35根,短跳绳25根。
学校原有篮球的数量占篮球和足球总数的,后来又买进12个篮球,这时篮球的数量占两种球总数的,这所学校现有篮球、足球共多少个?
原来的篮球占足球的
买进12个篮球后,篮球占足球的
-
=
=
答:学校现有篮球、足球共62个。
练一练:
练一练:
三个粮仓,甲仓库存粮120吨,乙仓库存的粮食占乙、丙两仓库和的丙仓存粮占甲、乙、丙三个仓库总和的,三个仓库共有存粮多少吨?
乙仓库占乙、丙两仓库和的
丙仓库占总数的
乙仓库占总数的:
乙仓库占丙仓的
120÷(1-
答:三个仓库共有存粮240吨。
甲仓库占丙仓的1-
总结:
这节课有什么收获?
同课章节目录
