中考备考攻坚课程第九讲:压轴题难点突破5:新定义阅读题 课件
文档属性
| 名称 | 中考备考攻坚课程第九讲:压轴题难点突破5:新定义阅读题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 11:28:23 | ||
图片预览







文档简介
(共52张PPT)
新定义型阅读理解题
罗湖外语实验学校
王少萍
罗湖区中考备考攻坚课程之压轴题难点突破5
知识技能梳理
01
分类讲解
02
目录
CONTENT
01
知识技能梳理
Part one
一、知识技能梳理
1、新定义的类型:
(1)定义新运算;
(2)定义初、高中衔接的"新知识";
(3)定义新概念
2、解决定义新概念的关键
正确理解新定义概念的意义.
(1)理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论.
(2)重视“举例”——利用“举例”检验是否理解“新定义”的意义,归纳“举例”提供的解题方法及分类方法。
(3)类比新定义中的概念、原理、方法,解决问题.
3、利用的数学思想
(1)转化的思想,把未知的问题转化为学过的知识。
(2)迁移的应用,对全新的概念,需要灵活的迁移运用。
(3)类比的思想。
02
分类讲解
Part two
二、分类讲解
新定义阅读理解题
以函数为载体
以三角形、四边形为载体
以圆为载体
模块一
以函数为载体
罗湖区中考备考攻坚课程之压轴题难点突破5
模块1 以函数为载体
P
C
J
K
模块1 以函数为载体
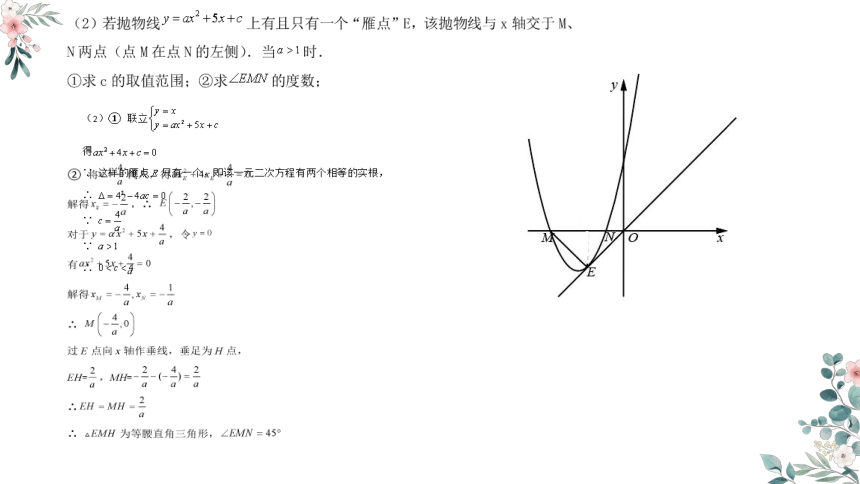
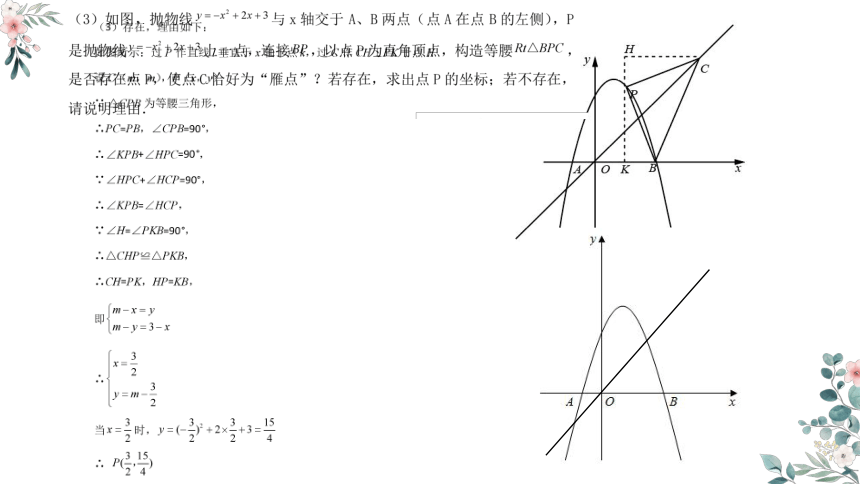
(4)如图,以M为原点,MN所在的直线为x轴建立平面直角坐标系xOy,
将函数y=﹣x的图象沿y轴正方向平移,直到与景观湖边界所在曲线有交点时停止,
设交点为E,过点E作EH⊥MN,垂足为H,
修建方案是:先沿MN方向修建到H处,再沿HE方向修建到E处.
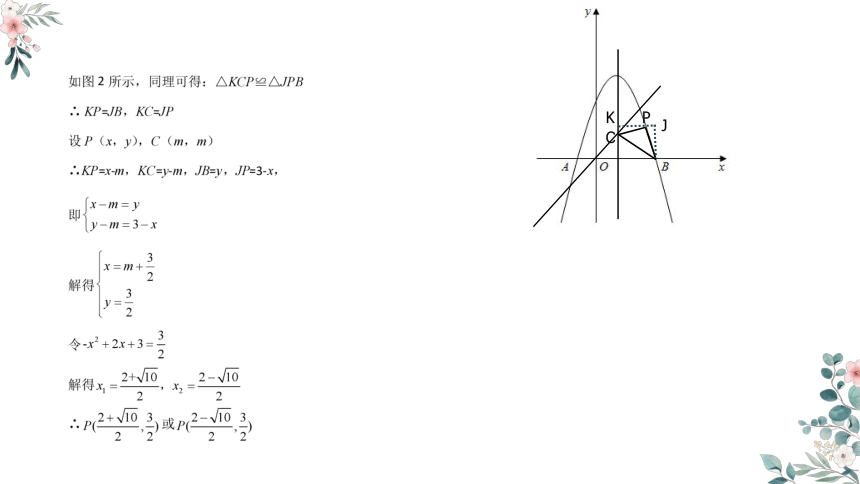
理由:设过点E的直线l1与x轴相交于点F.
在景观湖边界所在曲线上任取一点P,过点P作直线l2∥l1,l2与x轴相交于点G.
∵∠EFH=45°,
∴EH=HF,d(O,E)=OH+EH=OF,
同理d(O,P)=OG,
∵OG≥OF,
∴d(O,P)≥d(O,E),
∴上述方案修建的道路最短.
03
巩固练习
Part three
模块二
以三角形、四边形
为载体
罗湖区中考备考攻坚课程之压轴题难点突破5
模块2 以三角形、四边形为载体
例题1:以三角形为载体
【定义理解】如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5,则CP= .
(2)【类比探究】
①如图2,E是菱形ABCD一边上的中点,P是BE上的中点,则称AP是菱形ABCD的“双中线”,若AB=4,∠BAD=120°,则AP= .
②如图3,AP是矩形ABCD的“双中线”,若AB=4,BC=6,求AP的长.
(3)【拓展应用】
如图4,AP是平行四边形ABCD的“双中线”,若AB=4,BC=6,∠BAD=120°,求AP的长.
①如图2,E是菱形ABCD一边上的中点,P是BE上的中点,则称AP是菱形ABCD的“双中线”,若AB=4,∠BAD=120°,则AP= .
②如图3,AP是矩形ABCD的“双中线”,若AB=4,BC=6,求AP的长.
(3)【拓展应用】
如图4,AP是平行四边形ABCD的“双中线”,若AB=4,BC=6,∠BAD=120°,求AP的长.
模块2 以三角形、四边形为载体
(1)解:∵四边形ABCD为等邻角四边形,
∠A=130°,∠B=120°,
∴∠C=∠D,
∴∠D=55°,
故答案为:55;
(2)①证明:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵ED∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠ABD,
∴四边形ABDE为等邻角四边形;
②解:△BDC是等边三角形,理由如下:
∵∠BDC=∠C,
∴BD=BC,∠DBC=180°﹣2∠C,
∵∠A+∠E+∠ABD+∠BDE=360°,
∴∠A+∠E=360°﹣2∠ABD,
∵∠A+∠C+∠E=300°,
∴300°﹣∠C=360°﹣2(180°﹣2∠C),
∴∠C=60°,
又∵BD=BC,
∴△BDC是等边三角形;
巩固练习
模块三
以圆为载体
罗湖区中考备考攻坚课程之压轴题难点突破5
例题1
模块3 以圆为载体
例题2
03
巩固练习
Part three
感谢您的观看
新定义型阅读理解题
罗湖外语实验学校
王少萍
罗湖区中考备考攻坚课程之压轴题难点突破5
知识技能梳理
01
分类讲解
02
目录
CONTENT
01
知识技能梳理
Part one
一、知识技能梳理
1、新定义的类型:
(1)定义新运算;
(2)定义初、高中衔接的"新知识";
(3)定义新概念
2、解决定义新概念的关键
正确理解新定义概念的意义.
(1)理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论.
(2)重视“举例”——利用“举例”检验是否理解“新定义”的意义,归纳“举例”提供的解题方法及分类方法。
(3)类比新定义中的概念、原理、方法,解决问题.
3、利用的数学思想
(1)转化的思想,把未知的问题转化为学过的知识。
(2)迁移的应用,对全新的概念,需要灵活的迁移运用。
(3)类比的思想。
02
分类讲解
Part two
二、分类讲解
新定义阅读理解题
以函数为载体
以三角形、四边形为载体
以圆为载体
模块一
以函数为载体
罗湖区中考备考攻坚课程之压轴题难点突破5
模块1 以函数为载体
P
C
J
K
模块1 以函数为载体
(4)如图,以M为原点,MN所在的直线为x轴建立平面直角坐标系xOy,
将函数y=﹣x的图象沿y轴正方向平移,直到与景观湖边界所在曲线有交点时停止,
设交点为E,过点E作EH⊥MN,垂足为H,
修建方案是:先沿MN方向修建到H处,再沿HE方向修建到E处.
理由:设过点E的直线l1与x轴相交于点F.
在景观湖边界所在曲线上任取一点P,过点P作直线l2∥l1,l2与x轴相交于点G.
∵∠EFH=45°,
∴EH=HF,d(O,E)=OH+EH=OF,
同理d(O,P)=OG,
∵OG≥OF,
∴d(O,P)≥d(O,E),
∴上述方案修建的道路最短.
03
巩固练习
Part three
模块二
以三角形、四边形
为载体
罗湖区中考备考攻坚课程之压轴题难点突破5
模块2 以三角形、四边形为载体
例题1:以三角形为载体
【定义理解】如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5,则CP= .
(2)【类比探究】
①如图2,E是菱形ABCD一边上的中点,P是BE上的中点,则称AP是菱形ABCD的“双中线”,若AB=4,∠BAD=120°,则AP= .
②如图3,AP是矩形ABCD的“双中线”,若AB=4,BC=6,求AP的长.
(3)【拓展应用】
如图4,AP是平行四边形ABCD的“双中线”,若AB=4,BC=6,∠BAD=120°,求AP的长.
①如图2,E是菱形ABCD一边上的中点,P是BE上的中点,则称AP是菱形ABCD的“双中线”,若AB=4,∠BAD=120°,则AP= .
②如图3,AP是矩形ABCD的“双中线”,若AB=4,BC=6,求AP的长.
(3)【拓展应用】
如图4,AP是平行四边形ABCD的“双中线”,若AB=4,BC=6,∠BAD=120°,求AP的长.
模块2 以三角形、四边形为载体
(1)解:∵四边形ABCD为等邻角四边形,
∠A=130°,∠B=120°,
∴∠C=∠D,
∴∠D=55°,
故答案为:55;
(2)①证明:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵ED∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠ABD,
∴四边形ABDE为等邻角四边形;
②解:△BDC是等边三角形,理由如下:
∵∠BDC=∠C,
∴BD=BC,∠DBC=180°﹣2∠C,
∵∠A+∠E+∠ABD+∠BDE=360°,
∴∠A+∠E=360°﹣2∠ABD,
∵∠A+∠C+∠E=300°,
∴300°﹣∠C=360°﹣2(180°﹣2∠C),
∴∠C=60°,
又∵BD=BC,
∴△BDC是等边三角形;
巩固练习
模块三
以圆为载体
罗湖区中考备考攻坚课程之压轴题难点突破5
例题1
模块3 以圆为载体
例题2
03
巩固练习
Part three
感谢您的观看
同课章节目录
