中考备考攻坚课程第六讲:压轴题难点突破2:函数图像与性质应用探究题 课件
文档属性
| 名称 | 中考备考攻坚课程第六讲:压轴题难点突破2:函数图像与性质应用探究题 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 11:28:23 | ||
图片预览



文档简介
(共24张PPT)
2023罗湖区中考数学备考攻坚课程之压轴题难点突破2
第6讲 函数图象与性质应用探究题
模块一 函数图象及性质应用
(1)
例题1.在﹣4、﹣2,1、2四个数中、随机取两个数分别作为函数y=ax2+bx+1中a,b的值 , 利用列表或画树状图求该二次函数图象恰好经过第一、二、四象限的概率为 .
例题精讲
0
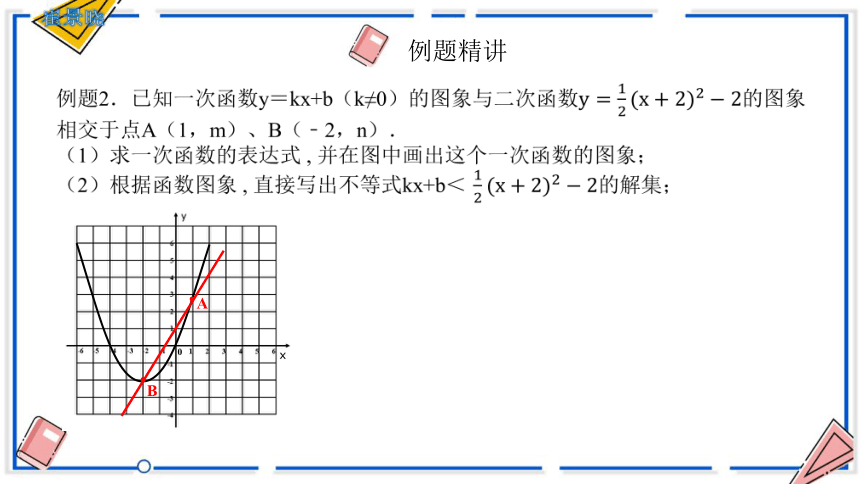
例题2.已知一次函数y=kx+b(k≠0)的图象与二次函数的图象相交于点A(1,m)、B(﹣2,n).
(1)求一次函数的表达式 , 并在图中画出这个一次函数的图象;
(2)根据函数图象 , 直接写出不等式kx+b<的解集;
例题精讲
B
.
A
.
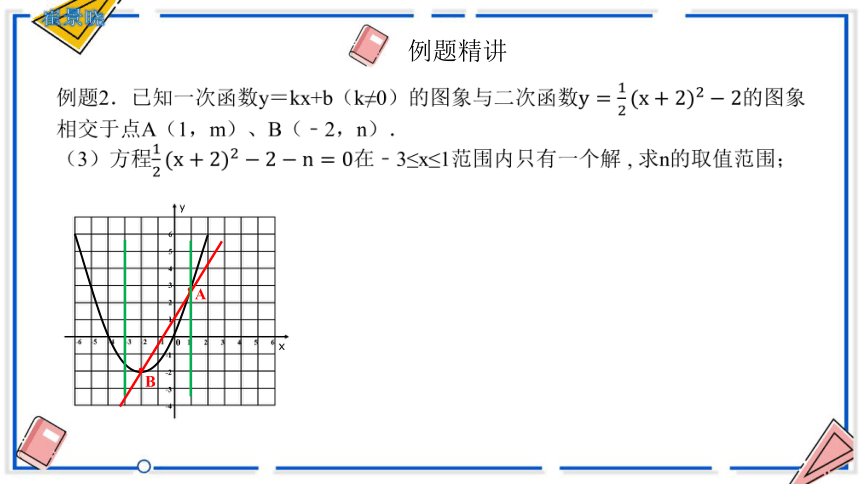
例题2.已知一次函数y=kx+b(k≠0)的图象与二次函数的图象相交于点A(1,m)、B(﹣2,n).
(3)方程在﹣3≤x≤1范围内只有一个解 , 求n的取值范围;
例题精讲
0
B
.
A
.
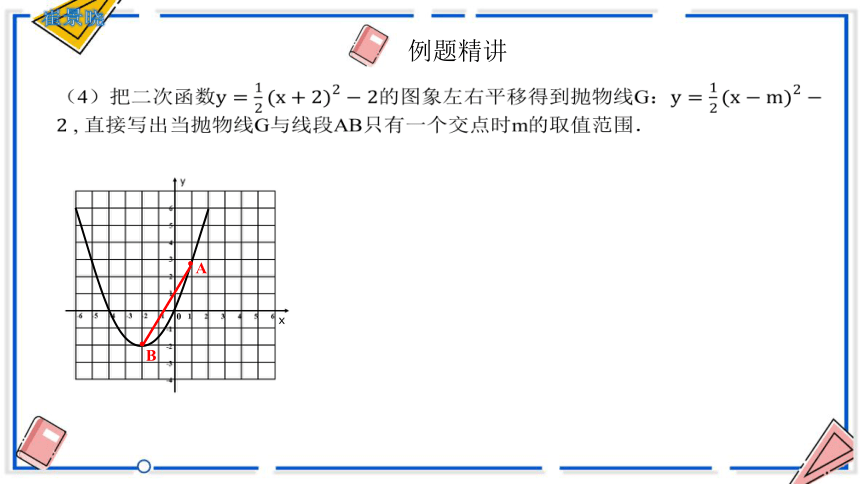
(4)把二次函数的图象左右平移得到抛物线G: , 直接写出当抛物线G与线段AB只有一个交点时m的取值范围.
例题精讲
0
B
.
A
.
0
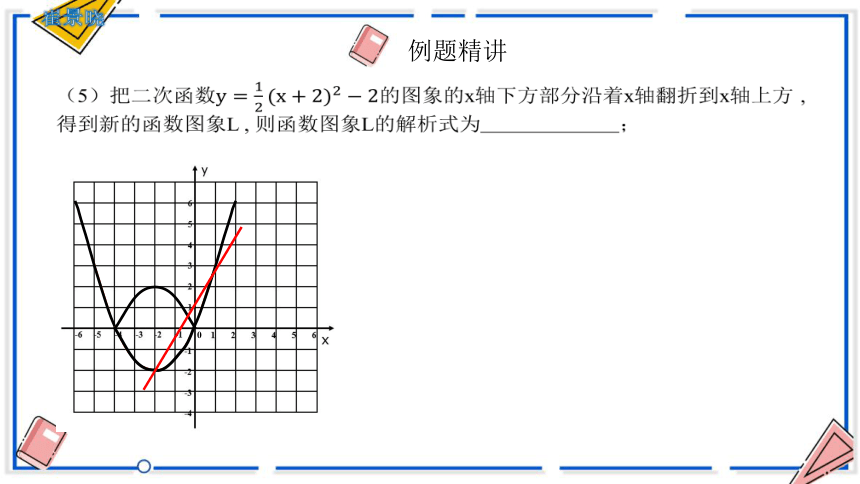
(5)把二次函数的图象的x轴下方部分沿着x轴翻折到x轴上方 , 得到新的函数图象L , 则函数图象L的解析式为;
例题精讲
0
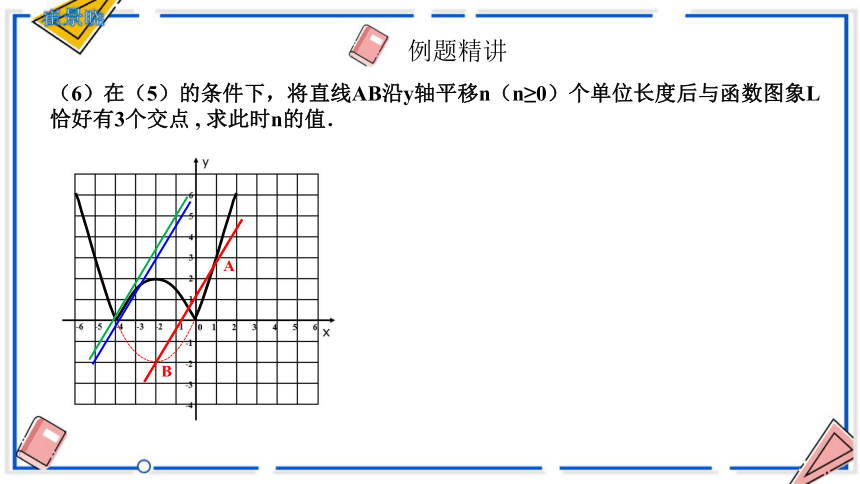
(6)在(5)的条件下,将直线AB沿y轴平移n(n≥0)个单位长度后与函数图象L恰好有3个交点 , 求此时n的值.
例题精讲
B
A
0
例题精讲
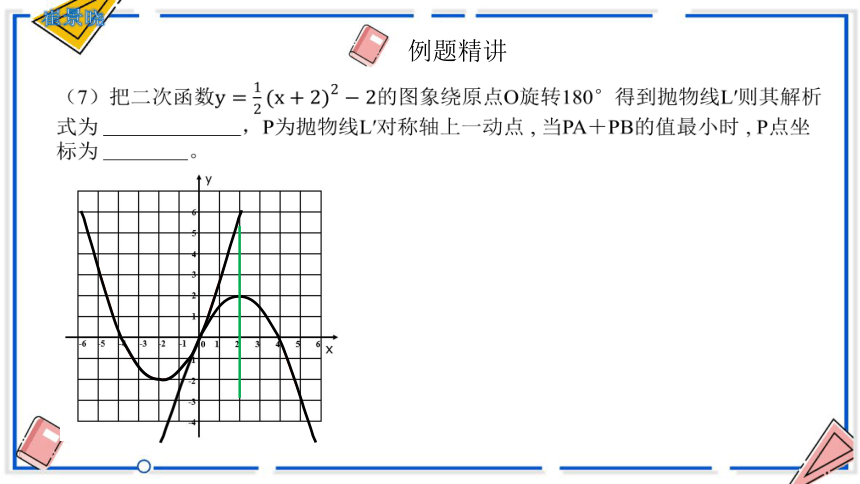
(7)把二次函数的图象绕原点O旋转180°得到抛物线L′则其解析式为,P为抛物线L′对称轴上一动点 , 当PA+PB的值最小时 , P点坐标为 。
模块二 函数图象与性质应用
(2)
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(1)当m=0时,若x1<x2,判断y1与y2的大小关系,并说明理由;
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
x
y
o
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
l
x = m
.
P
.
Q
.
M
.
N
x
y
o
图2
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
l
x = m
x
y
o
图3
.
P
(M)
.
Q (N)
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
P
(M)
.
Q
.
l
x = m
x
y
o
图4
N
.
例题4.已知直线l:y=kx+b经过点(0,7)和点(1,6).
(1)求直线l的解析式;
(2)若点P(m,n)在直线l上 , 以P为顶点的抛物线G过点(0,﹣3), 且开口下. ①求m的取值范围;
例题精讲
例题4.已知直线l:y=kx+b经过点(0,7)和点(1,6).
(2)若点P(m,n)在直线l上 , 以P为顶点的抛物线G过点(0,﹣3), 且开口下.
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单位长度后得到的点Q′也在G上时 , 求G在x1的图象的最高点的坐标.
例题精讲
模块三 函数图象及性质应用
(3)
例题5.【阅读】
通过构造恰当的图形 , 可以对线段长度、图形面积大小等进行比较 , 直观地得到一些不等关系或最值 , 这是“数形结合”思想的典型应用.
【理解】
(1)如图1 , AC⊥BC , CD⊥AB , 垂足分别为C、D , E是AB的中点 , 连接CE.已知AD=a , BD=b(0<a<b).
①分别求线段CE、CD的长(用含a、b的代数式表示);
②比较大小:CE CD(填“<”、“=”或“>”),
并用含a、b的代数式表示该大小关系.
例题精讲
【应用】
(2)如图2,在平面直角坐标系xOy中 , 点M、N在反比例函数y(x>0)的图象上 , 横坐标分别为m、n.设p=m+n , q,记lpq.
①当m=1 , n=2时,l= ;当m=3,n=3时 , l= ;
例题精讲
【应用】
(2)如图2,在平面直角坐标系xOy中 , 点M、N在反比例函数y(x>0)的图象上 , 横坐标分别为m、n.设p=m+n , q,记lpq.
②通过归纳猜想 , 可得l的最小值是 .请利用图2构造恰当的图形 , 并说明你的猜想成立.
例题精讲
.
M
.
N
.
J
A
C
B
E
G
F
例题6.学习了图形的旋转之后 , 小明知道 , 将点P绕着某定点A顺时针旋转一定的角度α , 能得到一个新的点P′ , 经过进一步探究 , 小明发现 , 当上述点P在某函数图象上运动时 , 点P′也随之运动 , 并且点P′的运动轨迹能形成一个新的图形.
试根据下列各题中所给的定点A的坐标、角度α的大小来解决相关问题.
【初步感知】
如图1,设A(1,1), α=90°, 点P是一次函数y=kx+b图象上的动点,已知该一次函数的图象经过点P1(﹣1,1).
(1)点P1旋转后 , 得到的点P1′的坐标为 ;
(2)若点P′的运动轨迹经过点P2′(2,1),
求原一次函数的表达式.
例题精讲
【深入感悟】
(3)如图2, 设A(0,0), α=45°, 点P是反比例函数y(x<0)的图象上的动点 , 过点P′作二、四象限角平分线的垂线 , 垂足为M,求△OMP′的面积.
例题精讲
图2
.
N
Q
M
【深入感悟】
(3)如图2, 设A(0,0), α=45°, 点P是反比例函数y(x<0)的图象上的动点 , 过点P′作二、四象限角平分线的垂线 , 垂足为M,求△OMP′的面积.
例题精讲
备用图
.
N’
.
p
.
P’
M
H
感谢聆听!
2023罗湖区中考数学备考攻坚课程之压轴题难点突破2
第6讲 函数图象与性质应用探究题
模块一 函数图象及性质应用
(1)
例题1.在﹣4、﹣2,1、2四个数中、随机取两个数分别作为函数y=ax2+bx+1中a,b的值 , 利用列表或画树状图求该二次函数图象恰好经过第一、二、四象限的概率为 .
例题精讲
0
例题2.已知一次函数y=kx+b(k≠0)的图象与二次函数的图象相交于点A(1,m)、B(﹣2,n).
(1)求一次函数的表达式 , 并在图中画出这个一次函数的图象;
(2)根据函数图象 , 直接写出不等式kx+b<的解集;
例题精讲
B
.
A
.
例题2.已知一次函数y=kx+b(k≠0)的图象与二次函数的图象相交于点A(1,m)、B(﹣2,n).
(3)方程在﹣3≤x≤1范围内只有一个解 , 求n的取值范围;
例题精讲
0
B
.
A
.
(4)把二次函数的图象左右平移得到抛物线G: , 直接写出当抛物线G与线段AB只有一个交点时m的取值范围.
例题精讲
0
B
.
A
.
0
(5)把二次函数的图象的x轴下方部分沿着x轴翻折到x轴上方 , 得到新的函数图象L , 则函数图象L的解析式为;
例题精讲
0
(6)在(5)的条件下,将直线AB沿y轴平移n(n≥0)个单位长度后与函数图象L恰好有3个交点 , 求此时n的值.
例题精讲
B
A
0
例题精讲
(7)把二次函数的图象绕原点O旋转180°得到抛物线L′则其解析式为,P为抛物线L′对称轴上一动点 , 当PA+PB的值最小时 , P点坐标为 。
模块二 函数图象与性质应用
(2)
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(1)当m=0时,若x1<x2,判断y1与y2的大小关系,并说明理由;
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
x
y
o
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
l
x = m
.
P
.
Q
.
M
.
N
x
y
o
图2
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
l
x = m
x
y
o
图3
.
P
(M)
.
Q (N)
例题3.在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
(2)若对于x1=m﹣2,x2=m+2,都有y1>y2,求m的取值范围.
例题精讲
P
(M)
.
Q
.
l
x = m
x
y
o
图4
N
.
例题4.已知直线l:y=kx+b经过点(0,7)和点(1,6).
(1)求直线l的解析式;
(2)若点P(m,n)在直线l上 , 以P为顶点的抛物线G过点(0,﹣3), 且开口下. ①求m的取值范围;
例题精讲
例题4.已知直线l:y=kx+b经过点(0,7)和点(1,6).
(2)若点P(m,n)在直线l上 , 以P为顶点的抛物线G过点(0,﹣3), 且开口下.
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单位长度后得到的点Q′也在G上时 , 求G在x1的图象的最高点的坐标.
例题精讲
模块三 函数图象及性质应用
(3)
例题5.【阅读】
通过构造恰当的图形 , 可以对线段长度、图形面积大小等进行比较 , 直观地得到一些不等关系或最值 , 这是“数形结合”思想的典型应用.
【理解】
(1)如图1 , AC⊥BC , CD⊥AB , 垂足分别为C、D , E是AB的中点 , 连接CE.已知AD=a , BD=b(0<a<b).
①分别求线段CE、CD的长(用含a、b的代数式表示);
②比较大小:CE CD(填“<”、“=”或“>”),
并用含a、b的代数式表示该大小关系.
例题精讲
【应用】
(2)如图2,在平面直角坐标系xOy中 , 点M、N在反比例函数y(x>0)的图象上 , 横坐标分别为m、n.设p=m+n , q,记lpq.
①当m=1 , n=2时,l= ;当m=3,n=3时 , l= ;
例题精讲
【应用】
(2)如图2,在平面直角坐标系xOy中 , 点M、N在反比例函数y(x>0)的图象上 , 横坐标分别为m、n.设p=m+n , q,记lpq.
②通过归纳猜想 , 可得l的最小值是 .请利用图2构造恰当的图形 , 并说明你的猜想成立.
例题精讲
.
M
.
N
.
J
A
C
B
E
G
F
例题6.学习了图形的旋转之后 , 小明知道 , 将点P绕着某定点A顺时针旋转一定的角度α , 能得到一个新的点P′ , 经过进一步探究 , 小明发现 , 当上述点P在某函数图象上运动时 , 点P′也随之运动 , 并且点P′的运动轨迹能形成一个新的图形.
试根据下列各题中所给的定点A的坐标、角度α的大小来解决相关问题.
【初步感知】
如图1,设A(1,1), α=90°, 点P是一次函数y=kx+b图象上的动点,已知该一次函数的图象经过点P1(﹣1,1).
(1)点P1旋转后 , 得到的点P1′的坐标为 ;
(2)若点P′的运动轨迹经过点P2′(2,1),
求原一次函数的表达式.
例题精讲
【深入感悟】
(3)如图2, 设A(0,0), α=45°, 点P是反比例函数y(x<0)的图象上的动点 , 过点P′作二、四象限角平分线的垂线 , 垂足为M,求△OMP′的面积.
例题精讲
图2
.
N
Q
M
【深入感悟】
(3)如图2, 设A(0,0), α=45°, 点P是反比例函数y(x<0)的图象上的动点 , 过点P′作二、四象限角平分线的垂线 , 垂足为M,求△OMP′的面积.
例题精讲
备用图
.
N’
.
p
.
P’
M
H
感谢聆听!
同课章节目录
