中考备考攻坚课程第四讲:填空题难点突破2:计算中的图形建构 课件
文档属性
| 名称 | 中考备考攻坚课程第四讲:填空题难点突破2:计算中的图形建构 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 11:28:23 | ||
图片预览


文档简介
(共21张PPT)
罗湖区2023中考数学培优课
第四讲 计算中的图形建构
模块一:熟练应用通法一题多解
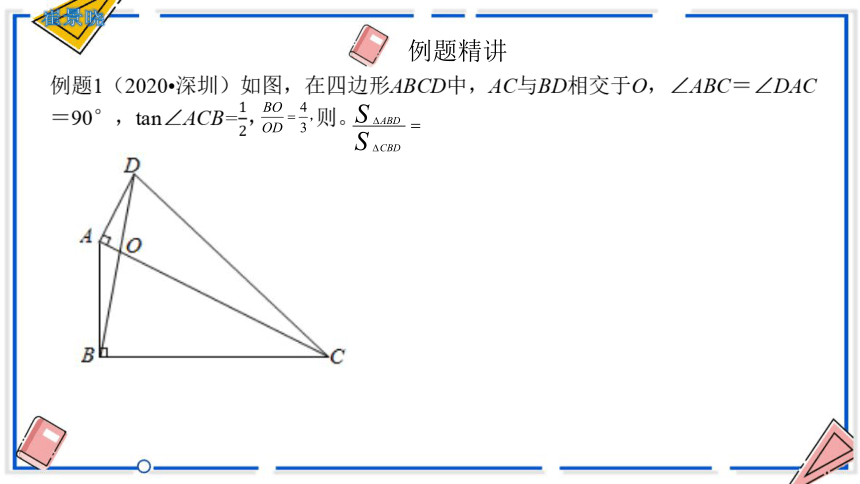
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
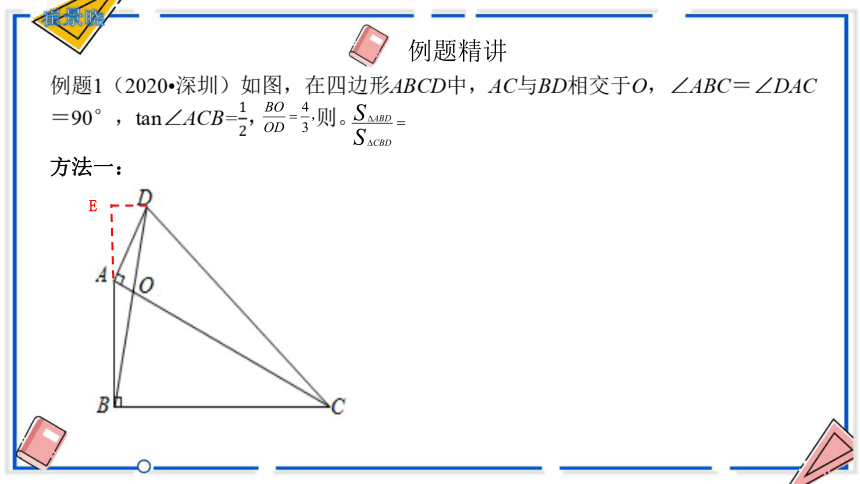
方法一:
E
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
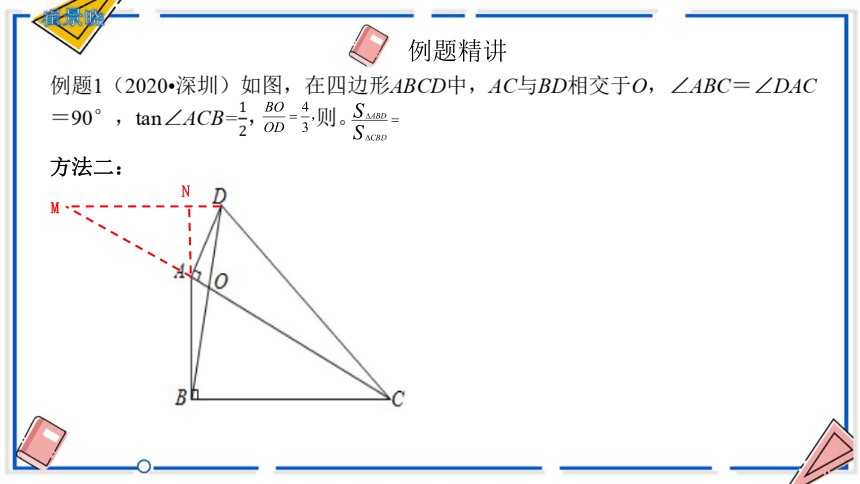
方法二:
N
M
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
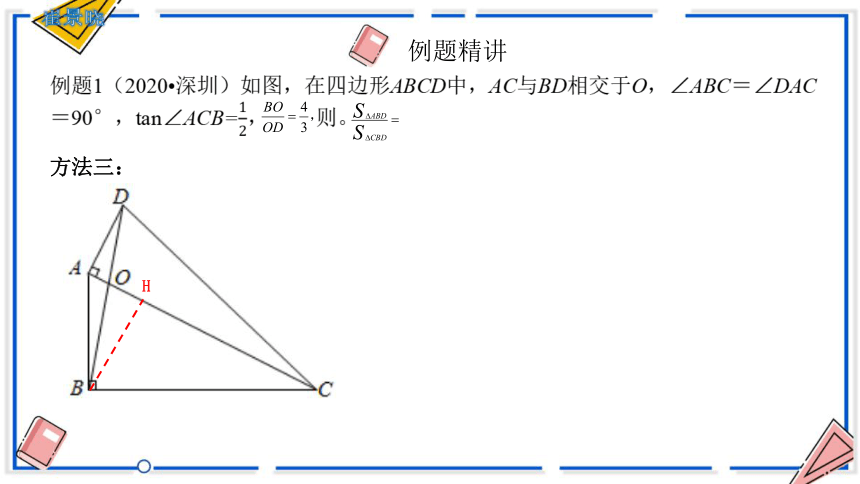
方法三:
H
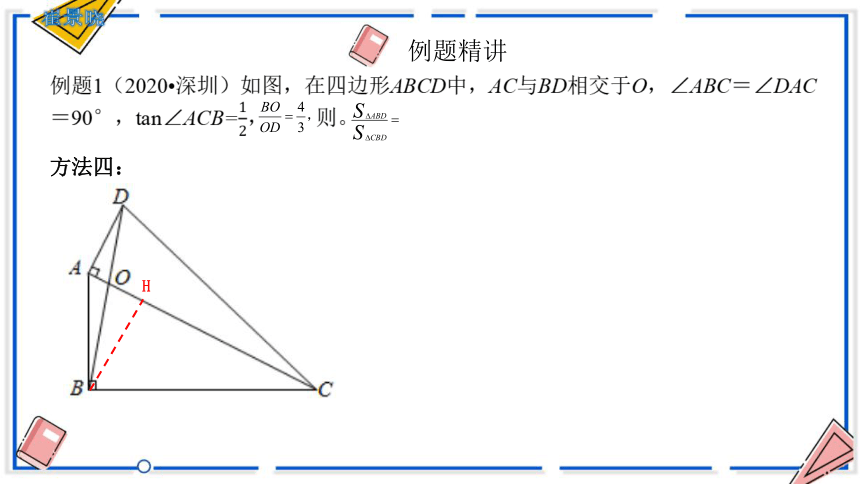
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
方法四:
H
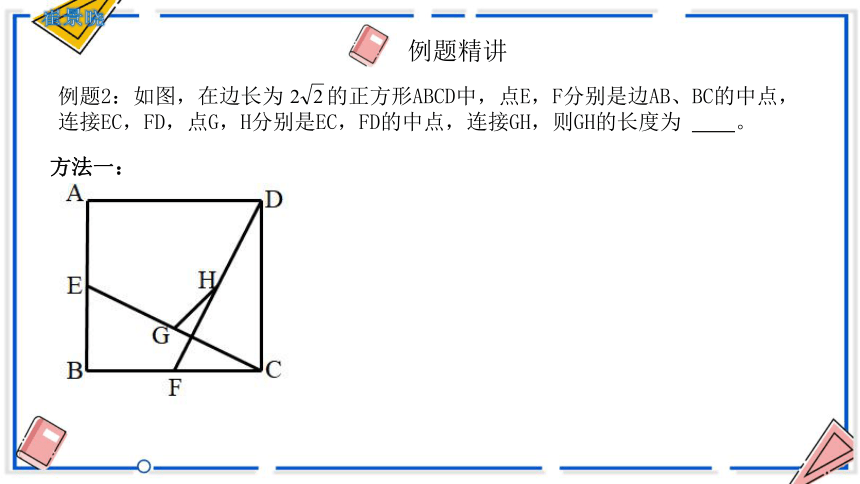
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法一:
P
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法二:
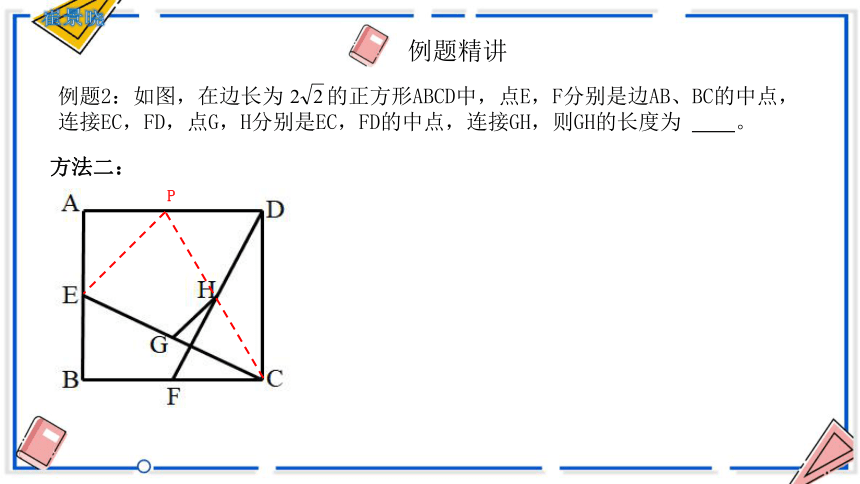
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法三:
M
P
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法四:
x
y
模块二:有效应用通法一题多变
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
1. 如图,在边长为6等边△ABC 中,点E,F分别是边AB,BC上的点,且AE=BF=2,连接EC,AF,点G,H分别是EC,FA的中点,连接GH,则GH的长度为 。
P
变式学习
M
2. 如图, 菱形ABCD 中, AB=8 , ∠D=60°;点F是CD的中点,点E是BC上一动点,连接AE, BF .G, H分别是AE, BF的中点, 连接GH , 则GH的最小是 .
Q
M
变式学习
3. 如图,正方形ABCD 的边长为4,点E,F分别为边BC,CD上一动点,且BE=CF.连接AE,BF相交于点P,点G,H分别是AE,BF的中点,连接GH,点Q为GH的中点.点E从点B运动到点C 的过程中,点P经过的路径长为 ,线段PQ扫过的面积为 .
O
J
.
变式学习
模块三:综合应用通法多解归一
图2
例题1,如图,矩形ABCD中,∠BAC=60°,点E在AB上,且BE:AB=1:3,点F在BC边上运动,以线段EF为斜边在点B的异侧作等腰直角三角形GEF,连接CG,当CG最小时,的值为.
图1
例题精讲
例题2,矩形ABCD中,∠ADB=30°,Rt△AEF中,∠EAF=90°,∠AFE=30°,将Rt△AEF绕A旋转至图中位置,使得点F落在BD上,此时,则此时=;
例题精讲
例题2变式引深:如图,Rt△ABC中,∠ACB=90°,,D为AB上一点,H为AC上一点,∠ABC=∠HDC,CB=CD,则 .
E
P
变式学习
感谢聆听!
罗湖区2023中考数学培优课
第四讲 计算中的图形建构
模块一:熟练应用通法一题多解
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
方法一:
E
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
方法二:
N
M
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
方法三:
H
例题1(2020 深圳)如图,在四边形ABCD中,AC与BD相交于O,∠ABC=∠DAC=90°,tan∠ACB=, 则。
例题精讲
方法四:
H
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法一:
P
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法二:
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法三:
M
P
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
方法四:
x
y
模块二:有效应用通法一题多变
例题精讲
例题2:如图,在边长为 的正方形ABCD中,点E,F分别是边AB、BC的中点,
连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 。
1. 如图,在边长为6等边△ABC 中,点E,F分别是边AB,BC上的点,且AE=BF=2,连接EC,AF,点G,H分别是EC,FA的中点,连接GH,则GH的长度为 。
P
变式学习
M
2. 如图, 菱形ABCD 中, AB=8 , ∠D=60°;点F是CD的中点,点E是BC上一动点,连接AE, BF .G, H分别是AE, BF的中点, 连接GH , 则GH的最小是 .
Q
M
变式学习
3. 如图,正方形ABCD 的边长为4,点E,F分别为边BC,CD上一动点,且BE=CF.连接AE,BF相交于点P,点G,H分别是AE,BF的中点,连接GH,点Q为GH的中点.点E从点B运动到点C 的过程中,点P经过的路径长为 ,线段PQ扫过的面积为 .
O
J
.
变式学习
模块三:综合应用通法多解归一
图2
例题1,如图,矩形ABCD中,∠BAC=60°,点E在AB上,且BE:AB=1:3,点F在BC边上运动,以线段EF为斜边在点B的异侧作等腰直角三角形GEF,连接CG,当CG最小时,的值为.
图1
例题精讲
例题2,矩形ABCD中,∠ADB=30°,Rt△AEF中,∠EAF=90°,∠AFE=30°,将Rt△AEF绕A旋转至图中位置,使得点F落在BD上,此时,则此时=;
例题精讲
例题2变式引深:如图,Rt△ABC中,∠ACB=90°,,D为AB上一点,H为AC上一点,∠ABC=∠HDC,CB=CD,则 .
E
P
变式学习
感谢聆听!
同课章节目录
