中考备考攻坚课程第二讲:选择题难点突破2:几何图形(轨迹)最值问题 课件
文档属性
| 名称 | 中考备考攻坚课程第二讲:选择题难点突破2:几何图形(轨迹)最值问题 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 40.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 11:28:23 | ||
图片预览




文档简介
(共19张PPT)
第二讲 几何图形轨迹(最值)问题
2023罗湖区数学备考攻坚课程之选择题难点突破2
学习目标
1、复习几何最值问题的基本图形以及辅助线的做法。
2、学会动点轨迹不明显的几何图形最值问题的方法
和技巧。
3、理解并体会转化思想在题目中的运用,会利用平移、
旋转、轴对称,三角函数,全等,相似,位似图形
性质等手段,构造出符合几何最值问题基本结构解决
问题。
复习回顾
主要是利用两个基本图形:
两点之间线段最短
垂线段最短
其他基本图形和结论:
三角形两边之和大于第三边,两边之差小于第三边
平行线之间,垂线段最短
点圆最值:点圆之间,点心线截距最短(长)
线圆最值:心垂线截距最短
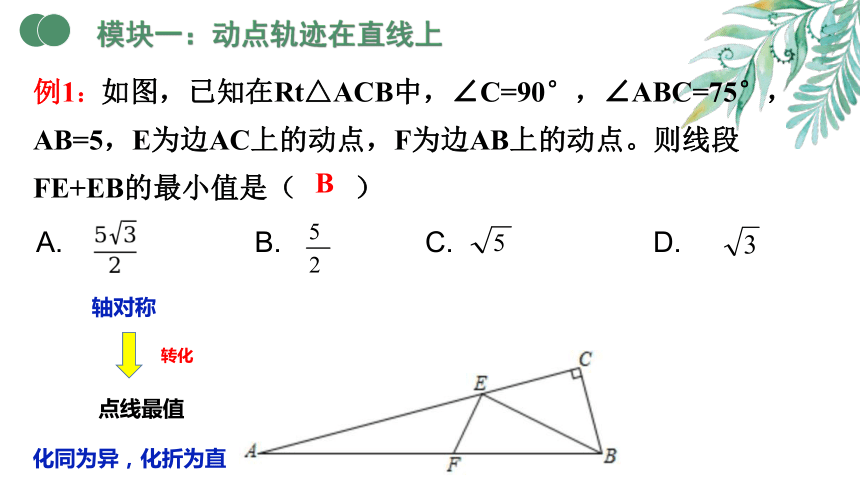
例1:如图,已知在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,E为边AC上的动点,F为边AB上的动点。则线段FE+EB的最小值是( )
A. B. C. D.
B
模块一:动点轨迹在直线上
转化
轴对称
化同为异,化折为直
点线最值
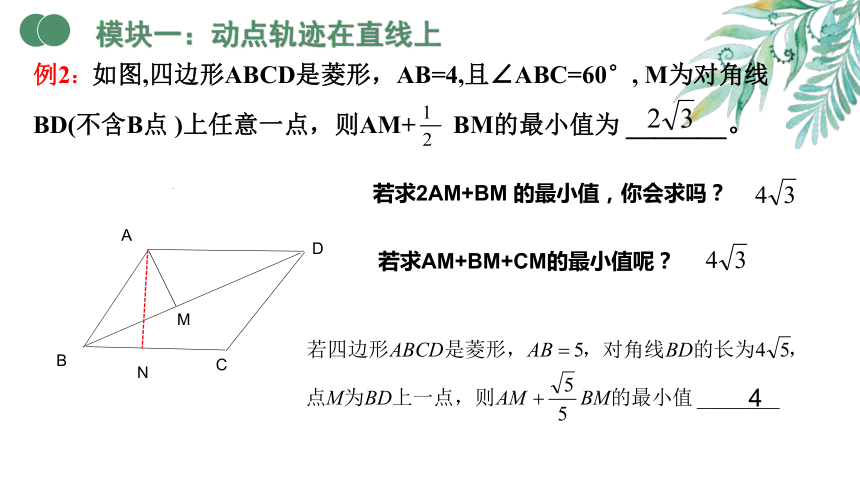
例2:如图,四边形ABCD是菱形,AB=4,且∠ABC=60°, M为对角线BD(不含B点 )上任意一点,则AM+ BM的最小值为 _______。
A
D
M
B
C
若求2AM+BM 的最小值,你会求吗?
若求AM+BM+CM的最小值呢?
模块一:动点轨迹在直线上
N
4
练习1:如图△ABC中,AB=AC=10.tanA=2, BE⊥AC于点 E,D是线段BE上的一个动点,则CD+ BD的最小值是( )
A. B. C. D.
B
模块一:动点轨迹在直线上
H
M
利用三角函数把系数不为1的线段转化为其他线段
模块一:动点轨迹在直线上
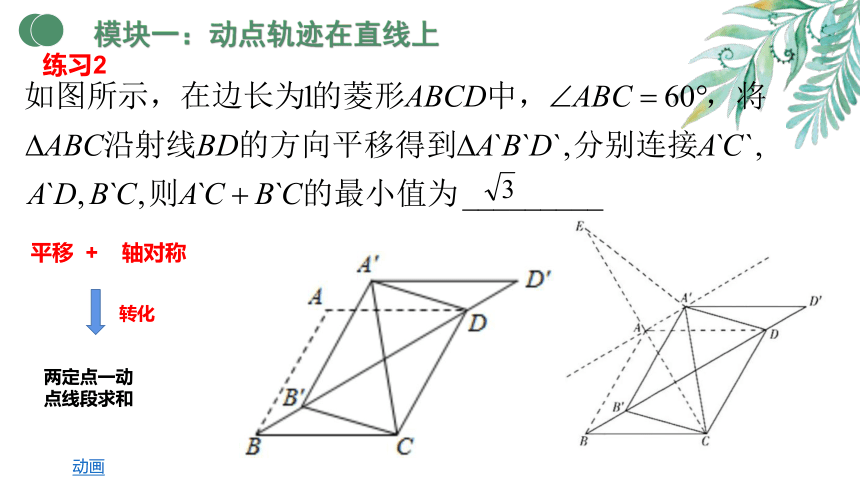
练移 + 轴对称
转化
两定点一动点线段求和
动画
例3:如图,在△ABC中,∠ACB=90°BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D,连接AD,BD,CD,则 AD+BD 的最小值为( )
A. B. C D.
B
B
D
C
A
模块二:动点轨迹在圆(弧)上
相似转化法
共角共边的相似
转化
两点之间线段最短
例4:如图,点A,B在圆O上,OA=OB=6.OA⊥OB.C是OA的中点,点D在OB上,且OD=4动点P在圆O上,则2PC+PD的最小值 _______。
O
C
A
P
D
B
模块二:动点轨迹在圆(弧)上
变式思考:
(1) (2)
练习1:已知半圆直径为8,P点是圆弧上的一动点,连接PA,PB,求PA+PB的最大值。
P
A
8
B
转换思维
模块二:动点轨迹在圆(弧)上
例5:如图,边长为4的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60 得到FC,连接DF, 则在点E运动过程中,DF的最小值是_______
你能画出点F的运动轨迹吗?
A
B
F
D
C
E
模块三:隐形轨迹问题
1
练习1如图①,在正方形ABCD中,AB=4,点P为平面内一点,PD=3,连接AP,将线段AP绕点A)顺时针旋转90°得到线段AQ.
(1)画出点Q的运动轨迹;
(2)如图②,连接 DQ,求DQ的最大值
Q
A
B
C
D
P
图一
A
D
Q
B
P
C
图二
模块三:隐形轨迹问题
动图
练习2:如图,在Rt△ABC中,∠ACB=90 ,AC=8,BC=6,点D是以A为圆心,4为半径的圆上一点,连接BD,M为BD的中点,则线段CM的长度的最大值为__________
.
模块三:隐形轨迹问题
动图
例6:如图,在边长为6的等边三角形ABC中,E,F分别是边AC,BC上的动点,且AE=CF,连接BE,AF交于点P,连接CP,则CP的最小值为_________。
你能画出点F的运动轨迹吗?
A
P
C
E
F
B
模块三:隐形轨迹问题
+
定边AB
点P在过A、B的圆上
练习3:如图,在△ABC中,∠BAC=90°,∠C=60°,点D在BC边上由点C向点B运动(不与点BC重合),过点D作DE⊥AD,交射线AB于点E若AB=6,则运动过程中线段AE长度的最小值为_____。
模块三:隐形轨迹问题
动图
练习4:如图,已知点A(2,4),点E(1,0),B为y轴正半轴上一动点,以A为直角顶点构造直角三角形ABC,AC交x轴于点C,D为BC边的中点,则DE的最小值为 ________。
A
B
O
D
C
E
模块三:隐形轨迹问题
动图
A
C
B
D
E
F
练习5: △ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F,如图2,若点D在△ABC内,∠DBC=20°,则∠BAF= _______;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长运动度的最小值是_________。
80°
模块三:隐形轨迹问题
动图
解决问题的主要方法是转化,
找到变化过程中不变的量或关系,
利用几何变换(比如等值变换:平移、旋转、轴对称;
比例变换:三角函数、相似图形性质)等手段
把所求量进行转化,构造出符合几何最值问题
理论依据的基本结构进而解决问题。
方法小结
再 见
第二讲 几何图形轨迹(最值)问题
2023罗湖区数学备考攻坚课程之选择题难点突破2
学习目标
1、复习几何最值问题的基本图形以及辅助线的做法。
2、学会动点轨迹不明显的几何图形最值问题的方法
和技巧。
3、理解并体会转化思想在题目中的运用,会利用平移、
旋转、轴对称,三角函数,全等,相似,位似图形
性质等手段,构造出符合几何最值问题基本结构解决
问题。
复习回顾
主要是利用两个基本图形:
两点之间线段最短
垂线段最短
其他基本图形和结论:
三角形两边之和大于第三边,两边之差小于第三边
平行线之间,垂线段最短
点圆最值:点圆之间,点心线截距最短(长)
线圆最值:心垂线截距最短
例1:如图,已知在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,E为边AC上的动点,F为边AB上的动点。则线段FE+EB的最小值是( )
A. B. C. D.
B
模块一:动点轨迹在直线上
转化
轴对称
化同为异,化折为直
点线最值
例2:如图,四边形ABCD是菱形,AB=4,且∠ABC=60°, M为对角线BD(不含B点 )上任意一点,则AM+ BM的最小值为 _______。
A
D
M
B
C
若求2AM+BM 的最小值,你会求吗?
若求AM+BM+CM的最小值呢?
模块一:动点轨迹在直线上
N
4
练习1:如图△ABC中,AB=AC=10.tanA=2, BE⊥AC于点 E,D是线段BE上的一个动点,则CD+ BD的最小值是( )
A. B. C. D.
B
模块一:动点轨迹在直线上
H
M
利用三角函数把系数不为1的线段转化为其他线段
模块一:动点轨迹在直线上
练移 + 轴对称
转化
两定点一动点线段求和
动画
例3:如图,在△ABC中,∠ACB=90°BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D,连接AD,BD,CD,则 AD+BD 的最小值为( )
A. B. C D.
B
B
D
C
A
模块二:动点轨迹在圆(弧)上
相似转化法
共角共边的相似
转化
两点之间线段最短
例4:如图,点A,B在圆O上,OA=OB=6.OA⊥OB.C是OA的中点,点D在OB上,且OD=4动点P在圆O上,则2PC+PD的最小值 _______。
O
C
A
P
D
B
模块二:动点轨迹在圆(弧)上
变式思考:
(1) (2)
练习1:已知半圆直径为8,P点是圆弧上的一动点,连接PA,PB,求PA+PB的最大值。
P
A
8
B
转换思维
模块二:动点轨迹在圆(弧)上
例5:如图,边长为4的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60 得到FC,连接DF, 则在点E运动过程中,DF的最小值是_______
你能画出点F的运动轨迹吗?
A
B
F
D
C
E
模块三:隐形轨迹问题
1
练习1如图①,在正方形ABCD中,AB=4,点P为平面内一点,PD=3,连接AP,将线段AP绕点A)顺时针旋转90°得到线段AQ.
(1)画出点Q的运动轨迹;
(2)如图②,连接 DQ,求DQ的最大值
Q
A
B
C
D
P
图一
A
D
Q
B
P
C
图二
模块三:隐形轨迹问题
动图
练习2:如图,在Rt△ABC中,∠ACB=90 ,AC=8,BC=6,点D是以A为圆心,4为半径的圆上一点,连接BD,M为BD的中点,则线段CM的长度的最大值为__________
.
模块三:隐形轨迹问题
动图
例6:如图,在边长为6的等边三角形ABC中,E,F分别是边AC,BC上的动点,且AE=CF,连接BE,AF交于点P,连接CP,则CP的最小值为_________。
你能画出点F的运动轨迹吗?
A
P
C
E
F
B
模块三:隐形轨迹问题
+
定边AB
点P在过A、B的圆上
练习3:如图,在△ABC中,∠BAC=90°,∠C=60°,点D在BC边上由点C向点B运动(不与点BC重合),过点D作DE⊥AD,交射线AB于点E若AB=6,则运动过程中线段AE长度的最小值为_____。
模块三:隐形轨迹问题
动图
练习4:如图,已知点A(2,4),点E(1,0),B为y轴正半轴上一动点,以A为直角顶点构造直角三角形ABC,AC交x轴于点C,D为BC边的中点,则DE的最小值为 ________。
A
B
O
D
C
E
模块三:隐形轨迹问题
动图
A
C
B
D
E
F
练习5: △ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F,如图2,若点D在△ABC内,∠DBC=20°,则∠BAF= _______;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长运动度的最小值是_________。
80°
模块三:隐形轨迹问题
动图
解决问题的主要方法是转化,
找到变化过程中不变的量或关系,
利用几何变换(比如等值变换:平移、旋转、轴对称;
比例变换:三角函数、相似图形性质)等手段
把所求量进行转化,构造出符合几何最值问题
理论依据的基本结构进而解决问题。
方法小结
再 见
同课章节目录
