中考备考攻坚课程第二讲:选择题难点突破2:几何图形轨迹最值问题 (教学设计)
文档属性
| 名称 | 中考备考攻坚课程第二讲:选择题难点突破2:几何图形轨迹最值问题 (教学设计) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 11:28:23 | ||
图片预览




文档简介
中考选择题难点突破2:《几何图形轨迹(最值)问题》
---------邓雪玲
知识梳理
几何图形轨迹最值问题是中考的热点问题,题型丰富,变化灵活,综合性强,考查的知识点众多,涉及数形结合、转化等多种数学思想,考查了学生的添加辅助线,依题画图,建构知识体系等能力,一般都是各题型的压轴题,发展了学生的几何直观和推理能力的核心素养。
初中数学的几何动点最值问题其实都来自两个基本图形:
定点到定点:两点之间,线段最短
定点到定线:点线之间,垂线段最短
在此基础上又产生了以下基础图形和结论:
三角形两边之和大于第三边,两边之差小于第三边
平行线之间,垂线段最短
点圆最值:点圆之间,点心线截距最短(长)
线圆最值:心垂线截距最短
解决几何最值问题的主要方法是转化,通过变化过程中不变特征的分析,利用几何变换(比如等值变换:平移、旋转、轴对称;比例变换:三角函数、相似图形性质)等手段把所求量进行转化,构造出符合几何最值问题理论依据的基本结构进而解决问题。
教学过程:
模块一:动点轨迹在直线上
【设计意图】通过尝试解决例1、例2,使学生体会:当动点轨迹明确是直线(或线段,射线)时,动中求静,找到变化过程中的不变量是解决问题的关键,可以利用对称,平移,三角函数等知识,化同为异,化折为直的思维方法解决,可以回顾将军饮马,建桥选址,胡不归等常见模型。
【例题精讲】
例1:如图,已知在中,,,,为边上的动点,为边上的动点。则线段的最小值是( )
A. B. C. D.
【解答】B
如图,作点关于的对称点,连接并延长交的延长线于,连接,
.
.
当三点共线且与垂直时,线段的值最小,即作于.在Rt中,.
例2:如图,四边形是菱形,AB=4,且,为对角线(不含点)上任意一点,则的最小值为___________。
变式思考:(1)本题若求“的最小值,你会求吗?
(2)本题若求“的最小值,你会求吗?
(3) 若四边形是菱形,,对角线的长为,点为上一点,则的最小值__________.
【解答】
如何将转化为其他线段呢?
本题值为,可转化为某一角的正弦值,即转化为角的正弦值.
思考到这里,不难发现,只要作垂直于点,则,即最小转化为最小,本题得解.
如图,作,垂足为交于点,
四边形是菱形且,
.
,
即的最小值为的长.
在Rt中,.
的最小值为.
【变式思考答案】(1)(2) (3)4
模块一:跟进练习解答
1、如图,在Rt中,,点是上的任意一点,作于点于点,连接,则的最小值为______。
【解答】2.4
中,,
连接CP
于点与点E
四边形是矩形
当DE最小时,则CP最小,根据垂线段最短可知时,最小
2、如图,中,为边上的一动点,则的最小值等于________.
【解答】
如图,过点作交延长线于点,
在Rt中,易得,当三点共线时,的值最小,此时,即的最小值为,
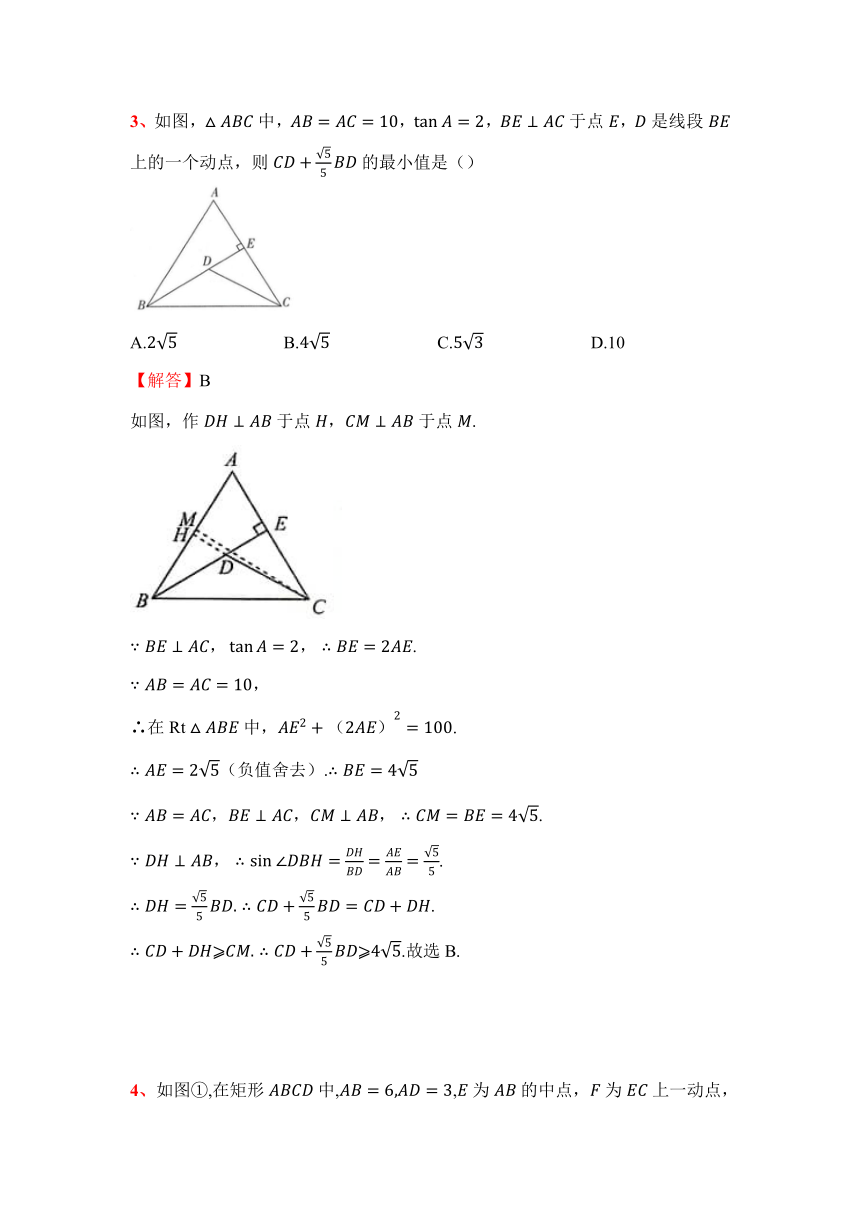
3、如图,中,,,于点,是线段上的一个动点,则的最小值是()
A. B. C. D.10
【解答】B
如图,作于点于点.
.
,
∴在中,.
(负值舍去).
.
.
.
.故选B.
4、如图①,在矩形中,,为的中点,为上一动点,为的中点.
(1)画出当从点运动到点时,点的运动轨迹;
(2)如图②,连接求的最小值.
【解答】
取的中点,连接并延长,交于点,连接点分别是的中点,为的中位线,在点运动的过程中,点始终在的中位线上运动.当时,取得最小值.
在矩形中,为的中点,
均为等腰直角三角形,,即的最小值即为的长,在Rt中,的最小值是
5、如图,在中,,,,交于点.点为线段上的动点,则的最小值为________.
【解答】.
过点作于点,过点作于点,首先得出,根据,得,则的最小值为的最小值,即求的长,再通过等积法即可解决问题.
过点作于点,过点作于点,
,
,
,,,
由勾股定理得,
,
,
.
即点三点共线时,最小,的最小值为的长,
,
,
的最小值为.
故答案为:.
6、如图所示,在边长为1的菱形中,,沿射线的方向平移得到,分别连接,则的最小值为_________
【解答】
作直线AA',并作点C关于直线的对称点E,连接EA,.
四边形为菱形,,由平移得,
当三点共线时,的值最小.
,
,,
即的最小值为.
方法总结求不在同一条直线上的两条线段长的和的最小值,一般是通过轴对称转化为求一条直线上的两条线段的长度和.
模块二:动点轨迹是圆(弧)
【设计意图】通过解决例3、例4,经历自主调用数学方法,运用数学思维分析探究的过程,相似转化法求最值。“PA+kPB”型的最值问题,当明确动点在圆上运动(阿氏圆问题),通过构造相似三角形,转化成两线段和的最小值。
【例题精讲】
例3:如图,在中,,以点为圆心,6为半径的圆上有一个动点,连接,则的最小值为()
A.3 B.4 C.5 D.6
【解答】B
在线段上截取,使得4,连接,
易得,
,即.
,
在Rt中,由勾股定理得的最小值为.
例4:如图,点在圆上,是的中点,点在上,且动点在圆上,则的最小值_________。
变式思考:(1)本题若求“”的最小值,你会求吗?
(2)本题若求“”的最小值,你会求吗?
【解答】
如何将转化为其他线段呢?不难发现本题出现了中点,即2倍关系,套用“阿氏圆”模型:构造共边共角相似.
连接,在射线上截取,连接交于点,此时的值最小.易知.
即三点共线时,最小.
在Rt中,.
即的最小值为.
【答案】(1)
模块二 跟踪练习解答
1、如图所示,,半径为2的圆内切于,为圆上一动点,过点作分别垂直于的两边,垂足为则的最大值__________
【解答】
作于,作于,如图所示:
当与 切时,取得最大和最小,
①连接,如图1所示:
可得:四边形为正方形,
在中,,
在Rt中,,
2、已知半圆直径为8,点是圆弧上的一动点,连接,求的最大值。
【解答】
3、点的坐标分别为(2,0),(0,2)点为坐标平面内的一点,,点为线段上的中点,连接,则的最大值为( )
A. B. C. D.
【解答】B
点为坐标平面内一点,点在以点为圆心、1为半径的圆上.如图,在轴上取,连接,
当三点共线时,最大,的最大值为.因此本题选B.
4、如图,正方形的边长为4,的半径为2,为上的动点,则的最大值是_______
【解答】5
如图,在上截取,连接
正方形的边长为的半径为2,
.
当三点共线时,值最小,即的值最小.
的最小值为.故答案为5.
5、正方形边长为4,为内切圆周上动点,求的最小值_________.
【解答】 如解图,连接,
设的半径为,则,取的中点,连接是公共角,当在一条直线上时,最小,最小值为的长,过点作于点最小值为的最小值是.
6、菱形边长为2,,圆的半径为,与圆相切于点,点在圆上运动,求的最小值_______。
【解答】
模块三:隐形轨迹问题
【设计意图】如果题目中并未直接给出动点轨迹,这时需要我们去分析和寻找动点的运动轨迹,这是学生最难掌握的难点,确定轨迹后,再根据轨迹确定属于哪种最值问题,再进行分析和计算。例5是通过旋转构造手拉手全等,找到动点运动轨迹是线段,从而转化成点到直线最值问题;例6的核心思路是:由结论入手:求的最小值,是定点,是动点,的轨迹如何?由可得,定弦定角,即点在圆上运动。
练习涉及主从联动问题---其实质是构造旋转型全等或相似,找到对应点的运动轨迹。隐圆问题---利用定点定长,定边对定角,定角动弦,四点共圆,找到动点的运动轨迹是圆,从而寻找圆心与半径,转化成点圆,线圆最值问题。
【例题精讲】
例5:如图,边长为4的等边三角形中,是对称轴上的一个动点,连接,将线段逆时针旋转60°得到,连接,则在点运动过程中,的最小值是__________
你能画出点F的运动轨迹吗?
【解答】1
找到点的轨迹是本题的首要任务,直线型轨迹的常用寻找方法都是寻找定点定角,即找到过某一定点的定角,点的轨迹即可确定.如图
本题中易得,则不难发现点的轨迹为直线.再根据垂线段最短,可得的最小值为1.
例6如图,在边长为6的等边三角形中,分别是边上的动点,且,连接交于点,连接,则的最小值为___________.
你能画出点F的运动轨迹吗?
【解答】
易证.
如图3-3-13,过点,点,点作,连接
点在上运动.
当点在上时,有最小值,的最小值.
模块三 跟踪练习解答
1、如图,在Rt中,,点是内部一点,且,连接,则的最小值为_______.
【解答】 轨迹描述:点在以为直径的圆弧上运动
(利用同角的余角相等得到定角,再根据模型解题就清晰明了了)点在以的中点为圆心,长为直径的弧上运动(直径所对的圆周角为,连接当三点共线时,取得最小值,最小值为的值..
2、如图①,在正方形中,,点为平面内一点,,连接,将线段绕点顺时针旋转90°,得到线段.
(1)画出求的运动轨迹。
(2)如图②,连接,求的最大值
【解答】
(1)如解图①,虚线即为点的运动轨迹;
(2)如解图②,连接.
将线段绕点顺时针旋转,得到线段,
点在以点为圆心,3为半径的上运动,当三点共线时,有最大值,
的最大值为.
3、如图,在中,,点在边上由点向点运动(不与点重合),过点作,交射线于点若,则运动过程中线段长度的最小值为_________.
【解答】4
取的中点,连接,如图.
在中,是斜边上的中线,.当最小时,最小,此时.(可考虑以为直径的圆与直线的交点情况,当圆与直线相切时,圆的半径最短.)
4、是边长为5的等边三角形,是边长为3的等边三角形,直线与直线交于点,如图,若点在内,,则_______;现将绕点旋转1周,在这个旋转过程中,线段长运动度的最小值是________.
【解答】80°;
都是等边三角形,.
如图,设交于点.
同法可证..点在的外接圆上运动,当最小时,的值最小,此时,
5、如图,在Rt中,点是以为圆心,4为半径的圆上一点,连接,为的中点,则线段的长度的最大值为______.
【解答】7
如图,取的中点,连接.
在Rt中,.因为是的中点,所以.因为是的中点,是的中点,所以.在中,,即.当三点共线时,或.所以线段长度的最大值为7.
6、如图,已知点,点,为轴正半轴上一动点,以为直角顶点构造直角三角形,交轴于点为边的中点,则的最小值为_______.
【解答】
本题的实质为有一直角绕点旋转与坐标轴交于两点,求的中点所形成的轨迹是什么的问题.由点坐标可构造一系列直角三角形,
发现所有三角形中(四点共圆),故所有满足题意的三角形相似,故确定的运动轨迹为一条直线的一部分.当在原点时,,此时点;当在原点时,,此时点在射线上.设直线的解析式为,
的解析式为.
当时,最小,此时.
故答案为.
---------邓雪玲
知识梳理
几何图形轨迹最值问题是中考的热点问题,题型丰富,变化灵活,综合性强,考查的知识点众多,涉及数形结合、转化等多种数学思想,考查了学生的添加辅助线,依题画图,建构知识体系等能力,一般都是各题型的压轴题,发展了学生的几何直观和推理能力的核心素养。
初中数学的几何动点最值问题其实都来自两个基本图形:
定点到定点:两点之间,线段最短
定点到定线:点线之间,垂线段最短
在此基础上又产生了以下基础图形和结论:
三角形两边之和大于第三边,两边之差小于第三边
平行线之间,垂线段最短
点圆最值:点圆之间,点心线截距最短(长)
线圆最值:心垂线截距最短
解决几何最值问题的主要方法是转化,通过变化过程中不变特征的分析,利用几何变换(比如等值变换:平移、旋转、轴对称;比例变换:三角函数、相似图形性质)等手段把所求量进行转化,构造出符合几何最值问题理论依据的基本结构进而解决问题。
教学过程:
模块一:动点轨迹在直线上
【设计意图】通过尝试解决例1、例2,使学生体会:当动点轨迹明确是直线(或线段,射线)时,动中求静,找到变化过程中的不变量是解决问题的关键,可以利用对称,平移,三角函数等知识,化同为异,化折为直的思维方法解决,可以回顾将军饮马,建桥选址,胡不归等常见模型。
【例题精讲】
例1:如图,已知在中,,,,为边上的动点,为边上的动点。则线段的最小值是( )
A. B. C. D.
【解答】B
如图,作点关于的对称点,连接并延长交的延长线于,连接,
.
.
当三点共线且与垂直时,线段的值最小,即作于.在Rt中,.
例2:如图,四边形是菱形,AB=4,且,为对角线(不含点)上任意一点,则的最小值为___________。
变式思考:(1)本题若求“的最小值,你会求吗?
(2)本题若求“的最小值,你会求吗?
(3) 若四边形是菱形,,对角线的长为,点为上一点,则的最小值__________.
【解答】
如何将转化为其他线段呢?
本题值为,可转化为某一角的正弦值,即转化为角的正弦值.
思考到这里,不难发现,只要作垂直于点,则,即最小转化为最小,本题得解.
如图,作,垂足为交于点,
四边形是菱形且,
.
,
即的最小值为的长.
在Rt中,.
的最小值为.
【变式思考答案】(1)(2) (3)4
模块一:跟进练习解答
1、如图,在Rt中,,点是上的任意一点,作于点于点,连接,则的最小值为______。
【解答】2.4
中,,
连接CP
于点与点E
四边形是矩形
当DE最小时,则CP最小,根据垂线段最短可知时,最小
2、如图,中,为边上的一动点,则的最小值等于________.
【解答】
如图,过点作交延长线于点,
在Rt中,易得,当三点共线时,的值最小,此时,即的最小值为,
3、如图,中,,,于点,是线段上的一个动点,则的最小值是()
A. B. C. D.10
【解答】B
如图,作于点于点.
.
,
∴在中,.
(负值舍去).
.
.
.
.故选B.
4、如图①,在矩形中,,为的中点,为上一动点,为的中点.
(1)画出当从点运动到点时,点的运动轨迹;
(2)如图②,连接求的最小值.
【解答】
取的中点,连接并延长,交于点,连接点分别是的中点,为的中位线,在点运动的过程中,点始终在的中位线上运动.当时,取得最小值.
在矩形中,为的中点,
均为等腰直角三角形,,即的最小值即为的长,在Rt中,的最小值是
5、如图,在中,,,,交于点.点为线段上的动点,则的最小值为________.
【解答】.
过点作于点,过点作于点,首先得出,根据,得,则的最小值为的最小值,即求的长,再通过等积法即可解决问题.
过点作于点,过点作于点,
,
,
,,,
由勾股定理得,
,
,
.
即点三点共线时,最小,的最小值为的长,
,
,
的最小值为.
故答案为:.
6、如图所示,在边长为1的菱形中,,沿射线的方向平移得到,分别连接,则的最小值为_________
【解答】
作直线AA',并作点C关于直线的对称点E,连接EA,.
四边形为菱形,,由平移得,
当三点共线时,的值最小.
,
,,
即的最小值为.
方法总结求不在同一条直线上的两条线段长的和的最小值,一般是通过轴对称转化为求一条直线上的两条线段的长度和.
模块二:动点轨迹是圆(弧)
【设计意图】通过解决例3、例4,经历自主调用数学方法,运用数学思维分析探究的过程,相似转化法求最值。“PA+kPB”型的最值问题,当明确动点在圆上运动(阿氏圆问题),通过构造相似三角形,转化成两线段和的最小值。
【例题精讲】
例3:如图,在中,,以点为圆心,6为半径的圆上有一个动点,连接,则的最小值为()
A.3 B.4 C.5 D.6
【解答】B
在线段上截取,使得4,连接,
易得,
,即.
,
在Rt中,由勾股定理得的最小值为.
例4:如图,点在圆上,是的中点,点在上,且动点在圆上,则的最小值_________。
变式思考:(1)本题若求“”的最小值,你会求吗?
(2)本题若求“”的最小值,你会求吗?
【解答】
如何将转化为其他线段呢?不难发现本题出现了中点,即2倍关系,套用“阿氏圆”模型:构造共边共角相似.
连接,在射线上截取,连接交于点,此时的值最小.易知.
即三点共线时,最小.
在Rt中,.
即的最小值为.
【答案】(1)
模块二 跟踪练习解答
1、如图所示,,半径为2的圆内切于,为圆上一动点,过点作分别垂直于的两边,垂足为则的最大值__________
【解答】
作于,作于,如图所示:
当与 切时,取得最大和最小,
①连接,如图1所示:
可得:四边形为正方形,
在中,,
在Rt中,,
2、已知半圆直径为8,点是圆弧上的一动点,连接,求的最大值。
【解答】
3、点的坐标分别为(2,0),(0,2)点为坐标平面内的一点,,点为线段上的中点,连接,则的最大值为( )
A. B. C. D.
【解答】B
点为坐标平面内一点,点在以点为圆心、1为半径的圆上.如图,在轴上取,连接,
当三点共线时,最大,的最大值为.因此本题选B.
4、如图,正方形的边长为4,的半径为2,为上的动点,则的最大值是_______
【解答】5
如图,在上截取,连接
正方形的边长为的半径为2,
.
当三点共线时,值最小,即的值最小.
的最小值为.故答案为5.
5、正方形边长为4,为内切圆周上动点,求的最小值_________.
【解答】 如解图,连接,
设的半径为,则,取的中点,连接是公共角,当在一条直线上时,最小,最小值为的长,过点作于点最小值为的最小值是.
6、菱形边长为2,,圆的半径为,与圆相切于点,点在圆上运动,求的最小值_______。
【解答】
模块三:隐形轨迹问题
【设计意图】如果题目中并未直接给出动点轨迹,这时需要我们去分析和寻找动点的运动轨迹,这是学生最难掌握的难点,确定轨迹后,再根据轨迹确定属于哪种最值问题,再进行分析和计算。例5是通过旋转构造手拉手全等,找到动点运动轨迹是线段,从而转化成点到直线最值问题;例6的核心思路是:由结论入手:求的最小值,是定点,是动点,的轨迹如何?由可得,定弦定角,即点在圆上运动。
练习涉及主从联动问题---其实质是构造旋转型全等或相似,找到对应点的运动轨迹。隐圆问题---利用定点定长,定边对定角,定角动弦,四点共圆,找到动点的运动轨迹是圆,从而寻找圆心与半径,转化成点圆,线圆最值问题。
【例题精讲】
例5:如图,边长为4的等边三角形中,是对称轴上的一个动点,连接,将线段逆时针旋转60°得到,连接,则在点运动过程中,的最小值是__________
你能画出点F的运动轨迹吗?
【解答】1
找到点的轨迹是本题的首要任务,直线型轨迹的常用寻找方法都是寻找定点定角,即找到过某一定点的定角,点的轨迹即可确定.如图
本题中易得,则不难发现点的轨迹为直线.再根据垂线段最短,可得的最小值为1.
例6如图,在边长为6的等边三角形中,分别是边上的动点,且,连接交于点,连接,则的最小值为___________.
你能画出点F的运动轨迹吗?
【解答】
易证.
如图3-3-13,过点,点,点作,连接
点在上运动.
当点在上时,有最小值,的最小值.
模块三 跟踪练习解答
1、如图,在Rt中,,点是内部一点,且,连接,则的最小值为_______.
【解答】 轨迹描述:点在以为直径的圆弧上运动
(利用同角的余角相等得到定角,再根据模型解题就清晰明了了)点在以的中点为圆心,长为直径的弧上运动(直径所对的圆周角为,连接当三点共线时,取得最小值,最小值为的值..
2、如图①,在正方形中,,点为平面内一点,,连接,将线段绕点顺时针旋转90°,得到线段.
(1)画出求的运动轨迹。
(2)如图②,连接,求的最大值
【解答】
(1)如解图①,虚线即为点的运动轨迹;
(2)如解图②,连接.
将线段绕点顺时针旋转,得到线段,
点在以点为圆心,3为半径的上运动,当三点共线时,有最大值,
的最大值为.
3、如图,在中,,点在边上由点向点运动(不与点重合),过点作,交射线于点若,则运动过程中线段长度的最小值为_________.
【解答】4
取的中点,连接,如图.
在中,是斜边上的中线,.当最小时,最小,此时.(可考虑以为直径的圆与直线的交点情况,当圆与直线相切时,圆的半径最短.)
4、是边长为5的等边三角形,是边长为3的等边三角形,直线与直线交于点,如图,若点在内,,则_______;现将绕点旋转1周,在这个旋转过程中,线段长运动度的最小值是________.
【解答】80°;
都是等边三角形,.
如图,设交于点.
同法可证..点在的外接圆上运动,当最小时,的值最小,此时,
5、如图,在Rt中,点是以为圆心,4为半径的圆上一点,连接,为的中点,则线段的长度的最大值为______.
【解答】7
如图,取的中点,连接.
在Rt中,.因为是的中点,所以.因为是的中点,是的中点,所以.在中,,即.当三点共线时,或.所以线段长度的最大值为7.
6、如图,已知点,点,为轴正半轴上一动点,以为直角顶点构造直角三角形,交轴于点为边的中点,则的最小值为_______.
【解答】
本题的实质为有一直角绕点旋转与坐标轴交于两点,求的中点所形成的轨迹是什么的问题.由点坐标可构造一系列直角三角形,
发现所有三角形中(四点共圆),故所有满足题意的三角形相似,故确定的运动轨迹为一条直线的一部分.当在原点时,,此时点;当在原点时,,此时点在射线上.设直线的解析式为,
的解析式为.
当时,最小,此时.
故答案为.
同课章节目录
