中考备考攻坚课程第三讲:填空题难点突破1;反比例函数中K值的计算 教学设计
文档属性
| 名称 | 中考备考攻坚课程第三讲:填空题难点突破1;反比例函数中K值的计算 教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 11:28:23 | ||
图片预览



文档简介
罗湖区中考数学培优课之填空题难点突破1
第三讲 反比例函数中的K值计算
翠园初级中学 秦晓莉
一、知识技能梳理
1.反比例函数比例系数的计算属于深圳中考的必考内容,近年多出现在填空题的倒数第二题,难易程度属于中度偏难一点,出现的形式多以反比例函数中K的几何意义与几何图形的性质和图形变换相结合,反比例函数与一次函数相结合。
2.解决反比例函数的题目,要抓住它的两个不变性,一是图象上的一个点的横纵坐标的乘积不变,二是和面积为|k|的矩形相联系的面积不变。在解决点的坐标或是面积的过程中,经常要用到如下线段的比值。
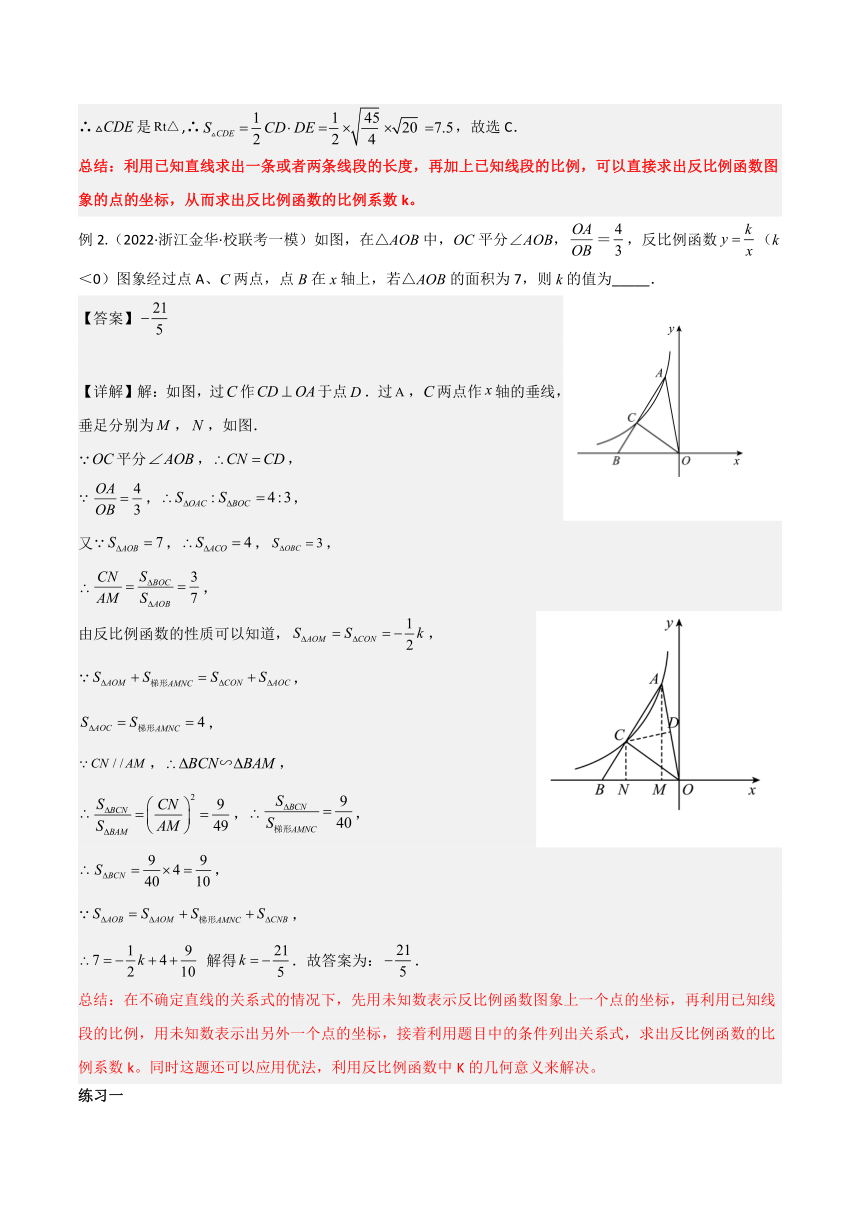
(1)如图①,过反比例函数上两点A,B,分别作坐标轴的垂线,垂足为C,D,则AB∥CD.
(2)如图②,过反比例函数图象上的点A,B分别向两条坐标轴作垂线,垂足分别为E,F,C,D,则AB∥CD∥EF.
(3)如图③,若一次函数与反比例函数交于点A,B,与坐标轴交于点C,D,则有
AC=BD;
(4)如图④,若一次函数与反比例函数交于点A,B,与坐标轴交于点C,D,则有
AC=BD .
3.数学思想:数形结合和转化思想。
二、学习过程
模块一:反比例函数与一次函数综合
例1(2022·广东深圳·深圳市宝安中学(集团)校考模拟预测)如图,直线y=2x+5
与x轴、y轴分别交于A、B两点,与反比例交于C、D两点,直线OD交反比例于点E,连接CE交y轴于点F,若CF:EF=1:4,则△DCE的面积为( )
A.8 B.5 C.7.5 D.6
【答案】C
【详解】解:∵直线y=2x+5与x轴、y轴分别交于A、B两点,
令得,令得,
∴,
如图,过点作轴的垂线,垂足分别为,
设,则,
∴,
∵,
∴,设,
∵CL⊥轴,轴,∴, ∴,∴,
∵轴,轴,∴,∴
设,则,∴,∴,∴,
∴,,
∵在上,∴,∴,解得,
∴,,
∴,,
∵关于对称,∴,
∴,,,
∵,
∴,
∴是,∴,故选C.
总结:利用已知直线求出一条或者两条线段的长度,再加上已知线段的比例,可以直接求出反比例函数图象的点的坐标,从而求出反比例函数的比例系数k。
例2.(2022·浙江金华·校联考一模)如图,在△AOB中,OC平分∠AOB,=,反比例函数(k<0)图象经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为_____.
【答案】
【详解】解:如图,过作于点.过,两点作轴的垂线,
垂足分别为,,如图.
平分,,
,,
又,,,
,
由反比例函数的性质可以知道,,
,
,
,,
,,
,
,
解得.故答案为:.
总结:在不确定直线的关系式的情况下,先用未知数表示反比例函数图象上一个点的坐标,再利用已知线段的比例,用未知数表示出另外一个点的坐标,接着利用题目中的条件列出关系式,求出反比例函数的比例系数k。同时这题还可以应用优法,利用反比例函数中K的几何意义来解决。
练习一
1.(2023春·八年级课时练习)如图,已知直线与轴交于点,与轴交于点,与双曲线交于、两点,若,则k的值为_____.
(对应例题1)
【答案】
【详解】解:在中,令,解得,则的坐标是;
令,解得:,则的坐标是,则.
,
作于点.则,
直线与反比例函数的交点是、,则根据题意得:,
即,解得:,,则,,
,,,,
是的角平分线,,
,解得:故答案是:.
2.如图,菱形的顶点与对角线交点都在反比例函数的图像上,对角线交轴于点,,且的面积为15,则______;延长交轴于点,则点的坐标为______.
(对应例题2)
【答案】 8
【详解】解:延长交轴于点,
设,则,,
∵,∴,
∴中,,,
∴,
∵,
∴,
∴
过作轴,则,
即,
∵,
∴,即.
∵,
∴,过点作于,易证,
∵,
∴,,
∴,联立得,
∴
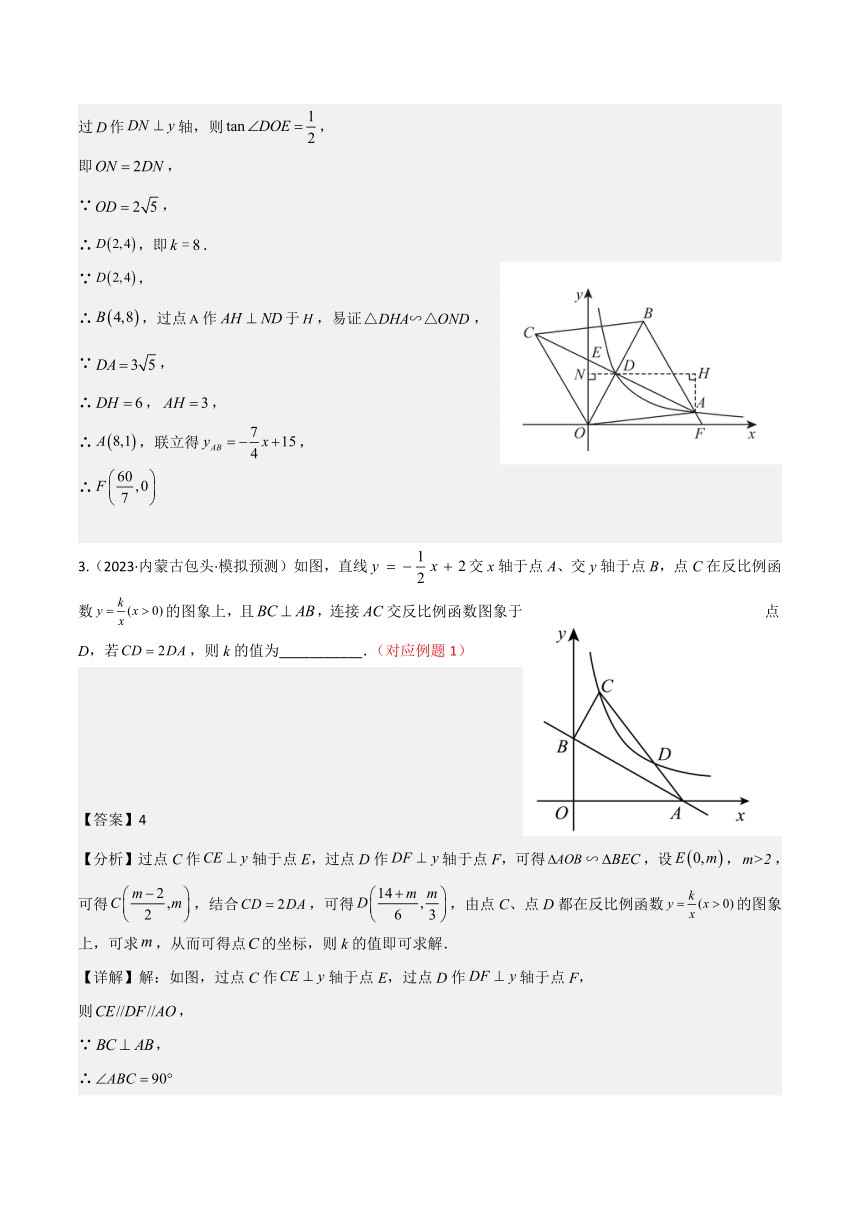
3.(2023·内蒙古包头·模拟预测)如图,直线交x轴于点A、交y轴于点B,点C在反比例函数的图象上,且,连接交反比例函数图象于点D,若,则k的值为___________.(对应例题1)
【答案】4
【分析】过点C作轴于点E,过点D作轴于点F,可得∽,设,,可得,结合,可得,由点C、点D都在反比例函数的图象上,可求,从而可得点的坐标,则k的值即可求解.
【详解】解:如图,过点C作轴于点E,过点D作轴于点F,
则,
∵,
∴
∴,
∵,
∴,
在与中,
,
∴∽,
∴.
∵直线交x轴于点A、交y轴于点B,
令,得;令,得,
∴,,
∴,,
∴,
即;
设,,
则,
∴,
∴,
∵,,
∴,即EF=2OF,
∴,
∵,
∴,
所以,
∴,
∵点C、点D都在反比例函数的图象上,
∴,
解得:(舍去)或,
∴,
∴.
故答案为:4.
4.(2023·陕西西安·校考模拟预测)如图,已知函数经过点,延长交双曲线另一分支于点C,过点A作直线交y轴正半轴于点D,交x轴负半轴于点E,交双曲线另一分支于点B,且.则的面积______.
(直线与双曲线的两支相交)
【答案】16
【详解】解:把点代入,
,
反比例函数的表达式为;
,
,
如图,过点作轴,垂足为,
,
,,
,
,
点,
,
,
,即;
设直线的表达式为:,
,
解得,
直线的表达式为:;
直线和反比例函数都关于原点对称,且,
EMBED Equation.DSMT4 ,
联立,
解得或,
,
过点作轴的平行线交于点,则,
,
.
模块二 :反比例函数中K的几何意义
例3.(2023春·江苏无锡·八年级江苏省锡山高级中学实验学校校考期中)如图,在平面直角坐标系中,O是斜边的中点,点A、E均在反比例函数图象上,延长线交x轴于点D,且,.则的面积为( )
A.9 B.12 C.18 D.24
【答案】B
【详解】解:如图,连接,
过点E作于点F,过点A作于点G,
∵.
∴点E的横纵坐标等于点A、D的横纵坐标之和的一半,
∴,,
∵点A、E均在反比例函数上,
∴,即,
∴,∴,∴,
∴,∴,∴,
∵O是斜边的中点,
∴,∴,∴,
∵,∴,∴,
∴.故选:B.
例4.(2021秋·重庆九龙坡·九年级重庆实验外国语学校校考期末)如图,在等腰中,,点为反比例函数(其中)图象上的一点,点在轴正半轴上,过点作,交反比例函数的图象于点,连接交于点,若的面积为2,则的值为( )
A.20 B. C.16 D.
【答案】A
【详解】解:如图,过点作交轴于,交于点,
,,,
,,
,,
,设,则,
,,,,
EMBED Equation.DSMT4 ,,
,,,
的面积为2,,,
,,,,,
,,,
,,.故选:A.
总结:认真观察,寻找面积为的三角形的面积,再结合线段的比值得出等底等高的三角形的面积的比,往往会帮我们更轻松地解题。
练习二
5.(2022·四川内江·四川省内江市第六中学校考二模)如图,已知双曲线y=(x<0)和y=(x>0),与直线交于点A,将直线OA向下平移与双曲线y=,与y轴分别交于点,与双曲线y=交于点,S△ABC=6,BP:CP=2:1,则k的值为____.
【答案】﹣3.
【详解】解:如图连接OB,OC,CF⊥y轴于F,过作轴于
∵OA∥BC,∴S△OBC=S△ABC=6,
∵,∴S△OPB=4,S△OPC=2,
∵S△OBE= ∴
EMBED Equation.DSMT4 轴,轴,
∵△BEP∽△CFP,
∴
∴S△OCF=,
∴.故答案为:.
6.(2020秋·重庆·九年级西南大学附中校考阶段练习)如图,等腰中,,双曲线经过的三个顶点,边交x轴于点D,原点O在上,若且面积为2,则k的值为( )
A.6 B.8 C.10 D.12
【答案】A
【详解】如图,过点A作轴于点E,
过点C作轴于点F,连接OA,
由反比例函数的性质可知,,
,∵OC=2CD
,
在和中,,
∴△COD∽△CAO
,
解得,
,
,
又∵AE⊥X轴,CF⊥X轴
,∴△ADE∽△CDF
,即,
解得,经检验,是所列分式方程的解,
则的值为6,故选:A.
7.(2021·新疆乌鲁木齐·校考一模)如图,点A,B分别是反比例函数和图象上的点,且轴,点C在x轴的正半轴上,连接交反比例函数的图象于点D,已知,,,则的值为______.
【答案】24
【详解】延长BD与x轴交于点M,连接OA,
∵轴,∴△ABD∽△CMD,AB⊥y轴,
∴AD:CD=BD:DM,
∵,∴,S△ABD=4S△CDM,
∴S△BOD:S△OMD=2:1,
∵,∴,∵,∴S△CDM=2,∴S△ABD=8,∵,,
∴S△AOD=16,
∵点A,B分别是反比例函数和图象上的点,
∵AB⊥y轴,∴,;
∵
∴,
∴,故答案为:24
8.(2022春·九年级课时练习)已知点A是双曲线在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.
【答案】
【详解】解:设A(a,),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=AO,
∵AO=,
∴CO=,
过点C作CD⊥x轴于点D,
则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即,
解得:y=,
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+,
将y=代入,可得:x2=,
故x=,y==,
则xy=﹣9,
故可得:(x>0).
故答案为:(x>0).
【点睛】本题考查了反比例函数的综合题,涉及了解直角三角形、等边三角形的性质及勾股定理的知识,综合考查的知识点较多,解答本题的关键是将所学知识融会贯通,注意培养自己解答综合题的能力.
模块三:反比例函数与几何综合
例5.(2023·浙江宁波·统考二模)如图,将矩形的顶点O与原点重合,边分别与x、y轴重合.将矩形沿折叠,使得点O落在边上的点F处,反比例函数上恰好经过E、F两点,若B点的坐标为,则k的值为________.
【答案】
【详解】解:连结OF,过E作于H.
由B点坐标为,可得E点的坐标为,F点的坐标为,
由折叠的性质知:是线段的垂直平分线,
∴,
EMBED Equation.DSMT4 ,
又,
,
,即,
,
,,
由折叠可得,
在中,由勾股定理可得
,
解得,(舍).故答案为:.
例6.(2023·江西抚州·金溪一中校考模拟预测)如图,中,,三个顶点A,B,C都在反比例函数的图象上,其中点A,C在第一象限,点B在第三象限,过坐标系原点O,交x轴于点D,连接,若,则的值为______.
【答案】
【详解】解:分别过点A、B作x轴的平行线,
交过点C平行于y轴的直线于点E、F,
∵过原点O,
,,
,,,
∵轴,,
设,则,
∴,
,,,,
,
,∴,
,,,,
解得:,,故答案为:.
总结:反比例函数和几何综合的问题,多围绕三角形的相似、四边形的几何性质和图性变换的几何性质来命题。通常是结合图形,借助交点和关键点的坐标及图形的几何特征列方程求解。
练习三
9.(2023·广西·统考一模)如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以为边,在第一象限内作矩形,且.将矩形翻折,使点B与原点O重合,折痕为,点C的对应点落在第四象限,过点M的反比例函数的图象恰好过的中点E,则点E的坐标为___________.
【答案】
【详解】解:如图,连接,过作于,
过作于,
由折叠的性质与矩形的性质可知,,,,
∵,,
∴,
∴,
∵为中点,即,
∴,即是线段的中点,
∴是的中位线,
∴,
令,则点坐标为,点坐标为,
∵均为反比例函数上的点,
∴,
解得,
∴点坐标为,
∴,
在中,由勾股定理得,即,
解得,
∵,
解得,
则,
∴点坐标为,故答案为:.
10.(2021·江苏无锡·统考二模)如图,在中,,,与轴交于点,,点在反比例函数的图象上,且轴平分,求_____.
【答案】
【详解】解:过A作AE⊥x轴,垂足为E,
∵C(0,-4),
∴OC=4,
∵∠AED=∠COD=90°,∠ADE=∠CDO
∴△ADE∽△CDO,
,
∴AE=1;
又∵y轴平分∠ACB,CO⊥BD,
∴BO=OD,
∵∠ABC=90°,
∴∠OCD=∠DAE=∠ABE=∠BCE,
∵∠DOC=∠ADE=90°
∴△ABE~△COD,
∴
设DE=n,则BO=OD=4n,BE=9n,
∴,
∴,
∴OE=5n=,
故点A(,1),∴k=×1=故答案为:.
11.(2023·江苏苏州·统考一模)如图,在平面直角坐标系中,菱形的边经过原点,,且顶点、、都在反比例函数的图像上,则顶点的坐标为______.
【答案】
【详解】解:如图所示,过点A作轴于N,
过点C作轴于M,连接,
设,则由对称性可知,
∴,
∵四边形是菱形,
∴,
又∵,∴是等边三角形,
∴,
∵轴,轴,
∴,∴,∴,
∴,∴,
∴,∴,
∵四边形是菱形,
∴点B平移到点A和点C平移到到点D的平移方式相同,
∴点D的坐标为,
又∵点D在反比例函数图象上,∴,
∴,∴,∴,
解得(负值舍去),∴,故答案为:.
12.(2020·湖南长沙·校联考二模)如图,点A,B分别在反比例函数y=(x<0)与y=(x>0)的图象上,且△OAB是等边三角形,则点A的坐标为_____.
【答案】(1﹣,﹣﹣1)
【详解】解:延长AB到C,使得BC=AB,连接OC,
作AM⊥x轴于M,CN⊥x轴于N.设A(m,).
∵△OAB是等边三角形,
∴OB=BA=BC,
∴∠AOC=90°,
∵∠OAC=60°,
∴∠ACO=30°,
∴OC=OA,
∵∠AMO=∠AOC=∠CNO=90°,
∴∠AOM+∠MAO=90°,∠AOM+∠CON=90°,
∴∠OAM=∠CON,
∴△AMO∽△ONC,
∴===,
∵OM=﹣m,AM=﹣,
∴ON=﹣,CN=﹣m,
∴C(﹣, m),
∴B(,),
∵点B在y=﹣上,
∴×=﹣4,
整理得:m4+4m2﹣4=0,
解得:m=1﹣(不合题意的根已经舍弃),
∴A(1﹣,﹣﹣1).
故答案为:(1﹣,﹣﹣1).
① ② ③ ④
第三讲 反比例函数中的K值计算
翠园初级中学 秦晓莉
一、知识技能梳理
1.反比例函数比例系数的计算属于深圳中考的必考内容,近年多出现在填空题的倒数第二题,难易程度属于中度偏难一点,出现的形式多以反比例函数中K的几何意义与几何图形的性质和图形变换相结合,反比例函数与一次函数相结合。
2.解决反比例函数的题目,要抓住它的两个不变性,一是图象上的一个点的横纵坐标的乘积不变,二是和面积为|k|的矩形相联系的面积不变。在解决点的坐标或是面积的过程中,经常要用到如下线段的比值。
(1)如图①,过反比例函数上两点A,B,分别作坐标轴的垂线,垂足为C,D,则AB∥CD.
(2)如图②,过反比例函数图象上的点A,B分别向两条坐标轴作垂线,垂足分别为E,F,C,D,则AB∥CD∥EF.
(3)如图③,若一次函数与反比例函数交于点A,B,与坐标轴交于点C,D,则有
AC=BD;
(4)如图④,若一次函数与反比例函数交于点A,B,与坐标轴交于点C,D,则有
AC=BD .
3.数学思想:数形结合和转化思想。
二、学习过程
模块一:反比例函数与一次函数综合
例1(2022·广东深圳·深圳市宝安中学(集团)校考模拟预测)如图,直线y=2x+5
与x轴、y轴分别交于A、B两点,与反比例交于C、D两点,直线OD交反比例于点E,连接CE交y轴于点F,若CF:EF=1:4,则△DCE的面积为( )
A.8 B.5 C.7.5 D.6
【答案】C
【详解】解:∵直线y=2x+5与x轴、y轴分别交于A、B两点,
令得,令得,
∴,
如图,过点作轴的垂线,垂足分别为,
设,则,
∴,
∵,
∴,设,
∵CL⊥轴,轴,∴, ∴,∴,
∵轴,轴,∴,∴
设,则,∴,∴,∴,
∴,,
∵在上,∴,∴,解得,
∴,,
∴,,
∵关于对称,∴,
∴,,,
∵,
∴,
∴是,∴,故选C.
总结:利用已知直线求出一条或者两条线段的长度,再加上已知线段的比例,可以直接求出反比例函数图象的点的坐标,从而求出反比例函数的比例系数k。
例2.(2022·浙江金华·校联考一模)如图,在△AOB中,OC平分∠AOB,=,反比例函数(k<0)图象经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为_____.
【答案】
【详解】解:如图,过作于点.过,两点作轴的垂线,
垂足分别为,,如图.
平分,,
,,
又,,,
,
由反比例函数的性质可以知道,,
,
,
,,
,,
,
,
解得.故答案为:.
总结:在不确定直线的关系式的情况下,先用未知数表示反比例函数图象上一个点的坐标,再利用已知线段的比例,用未知数表示出另外一个点的坐标,接着利用题目中的条件列出关系式,求出反比例函数的比例系数k。同时这题还可以应用优法,利用反比例函数中K的几何意义来解决。
练习一
1.(2023春·八年级课时练习)如图,已知直线与轴交于点,与轴交于点,与双曲线交于、两点,若,则k的值为_____.
(对应例题1)
【答案】
【详解】解:在中,令,解得,则的坐标是;
令,解得:,则的坐标是,则.
,
作于点.则,
直线与反比例函数的交点是、,则根据题意得:,
即,解得:,,则,,
,,,,
是的角平分线,,
,解得:故答案是:.
2.如图,菱形的顶点与对角线交点都在反比例函数的图像上,对角线交轴于点,,且的面积为15,则______;延长交轴于点,则点的坐标为______.
(对应例题2)
【答案】 8
【详解】解:延长交轴于点,
设,则,,
∵,∴,
∴中,,,
∴,
∵,
∴,
∴
过作轴,则,
即,
∵,
∴,即.
∵,
∴,过点作于,易证,
∵,
∴,,
∴,联立得,
∴
3.(2023·内蒙古包头·模拟预测)如图,直线交x轴于点A、交y轴于点B,点C在反比例函数的图象上,且,连接交反比例函数图象于点D,若,则k的值为___________.(对应例题1)
【答案】4
【分析】过点C作轴于点E,过点D作轴于点F,可得∽,设,,可得,结合,可得,由点C、点D都在反比例函数的图象上,可求,从而可得点的坐标,则k的值即可求解.
【详解】解:如图,过点C作轴于点E,过点D作轴于点F,
则,
∵,
∴
∴,
∵,
∴,
在与中,
,
∴∽,
∴.
∵直线交x轴于点A、交y轴于点B,
令,得;令,得,
∴,,
∴,,
∴,
即;
设,,
则,
∴,
∴,
∵,,
∴,即EF=2OF,
∴,
∵,
∴,
所以,
∴,
∵点C、点D都在反比例函数的图象上,
∴,
解得:(舍去)或,
∴,
∴.
故答案为:4.
4.(2023·陕西西安·校考模拟预测)如图,已知函数经过点,延长交双曲线另一分支于点C,过点A作直线交y轴正半轴于点D,交x轴负半轴于点E,交双曲线另一分支于点B,且.则的面积______.
(直线与双曲线的两支相交)
【答案】16
【详解】解:把点代入,
,
反比例函数的表达式为;
,
,
如图,过点作轴,垂足为,
,
,,
,
,
点,
,
,
,即;
设直线的表达式为:,
,
解得,
直线的表达式为:;
直线和反比例函数都关于原点对称,且,
EMBED Equation.DSMT4 ,
联立,
解得或,
,
过点作轴的平行线交于点,则,
,
.
模块二 :反比例函数中K的几何意义
例3.(2023春·江苏无锡·八年级江苏省锡山高级中学实验学校校考期中)如图,在平面直角坐标系中,O是斜边的中点,点A、E均在反比例函数图象上,延长线交x轴于点D,且,.则的面积为( )
A.9 B.12 C.18 D.24
【答案】B
【详解】解:如图,连接,
过点E作于点F,过点A作于点G,
∵.
∴点E的横纵坐标等于点A、D的横纵坐标之和的一半,
∴,,
∵点A、E均在反比例函数上,
∴,即,
∴,∴,∴,
∴,∴,∴,
∵O是斜边的中点,
∴,∴,∴,
∵,∴,∴,
∴.故选:B.
例4.(2021秋·重庆九龙坡·九年级重庆实验外国语学校校考期末)如图,在等腰中,,点为反比例函数(其中)图象上的一点,点在轴正半轴上,过点作,交反比例函数的图象于点,连接交于点,若的面积为2,则的值为( )
A.20 B. C.16 D.
【答案】A
【详解】解:如图,过点作交轴于,交于点,
,,,
,,
,,
,设,则,
,,,,
EMBED Equation.DSMT4 ,,
,,,
的面积为2,,,
,,,,,
,,,
,,.故选:A.
总结:认真观察,寻找面积为的三角形的面积,再结合线段的比值得出等底等高的三角形的面积的比,往往会帮我们更轻松地解题。
练习二
5.(2022·四川内江·四川省内江市第六中学校考二模)如图,已知双曲线y=(x<0)和y=(x>0),与直线交于点A,将直线OA向下平移与双曲线y=,与y轴分别交于点,与双曲线y=交于点,S△ABC=6,BP:CP=2:1,则k的值为____.
【答案】﹣3.
【详解】解:如图连接OB,OC,CF⊥y轴于F,过作轴于
∵OA∥BC,∴S△OBC=S△ABC=6,
∵,∴S△OPB=4,S△OPC=2,
∵S△OBE= ∴
EMBED Equation.DSMT4 轴,轴,
∵△BEP∽△CFP,
∴
∴S△OCF=,
∴.故答案为:.
6.(2020秋·重庆·九年级西南大学附中校考阶段练习)如图,等腰中,,双曲线经过的三个顶点,边交x轴于点D,原点O在上,若且面积为2,则k的值为( )
A.6 B.8 C.10 D.12
【答案】A
【详解】如图,过点A作轴于点E,
过点C作轴于点F,连接OA,
由反比例函数的性质可知,,
,∵OC=2CD
,
在和中,,
∴△COD∽△CAO
,
解得,
,
,
又∵AE⊥X轴,CF⊥X轴
,∴△ADE∽△CDF
,即,
解得,经检验,是所列分式方程的解,
则的值为6,故选:A.
7.(2021·新疆乌鲁木齐·校考一模)如图,点A,B分别是反比例函数和图象上的点,且轴,点C在x轴的正半轴上,连接交反比例函数的图象于点D,已知,,,则的值为______.
【答案】24
【详解】延长BD与x轴交于点M,连接OA,
∵轴,∴△ABD∽△CMD,AB⊥y轴,
∴AD:CD=BD:DM,
∵,∴,S△ABD=4S△CDM,
∴S△BOD:S△OMD=2:1,
∵,∴,∵,∴S△CDM=2,∴S△ABD=8,∵,,
∴S△AOD=16,
∵点A,B分别是反比例函数和图象上的点,
∵AB⊥y轴,∴,;
∵
∴,
∴,故答案为:24
8.(2022春·九年级课时练习)已知点A是双曲线在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.
【答案】
【详解】解:设A(a,),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=AO,
∵AO=,
∴CO=,
过点C作CD⊥x轴于点D,
则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即,
解得:y=,
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+,
将y=代入,可得:x2=,
故x=,y==,
则xy=﹣9,
故可得:(x>0).
故答案为:(x>0).
【点睛】本题考查了反比例函数的综合题,涉及了解直角三角形、等边三角形的性质及勾股定理的知识,综合考查的知识点较多,解答本题的关键是将所学知识融会贯通,注意培养自己解答综合题的能力.
模块三:反比例函数与几何综合
例5.(2023·浙江宁波·统考二模)如图,将矩形的顶点O与原点重合,边分别与x、y轴重合.将矩形沿折叠,使得点O落在边上的点F处,反比例函数上恰好经过E、F两点,若B点的坐标为,则k的值为________.
【答案】
【详解】解:连结OF,过E作于H.
由B点坐标为,可得E点的坐标为,F点的坐标为,
由折叠的性质知:是线段的垂直平分线,
∴,
EMBED Equation.DSMT4 ,
又,
,
,即,
,
,,
由折叠可得,
在中,由勾股定理可得
,
解得,(舍).故答案为:.
例6.(2023·江西抚州·金溪一中校考模拟预测)如图,中,,三个顶点A,B,C都在反比例函数的图象上,其中点A,C在第一象限,点B在第三象限,过坐标系原点O,交x轴于点D,连接,若,则的值为______.
【答案】
【详解】解:分别过点A、B作x轴的平行线,
交过点C平行于y轴的直线于点E、F,
∵过原点O,
,,
,,,
∵轴,,
设,则,
∴,
,,,,
,
,∴,
,,,,
解得:,,故答案为:.
总结:反比例函数和几何综合的问题,多围绕三角形的相似、四边形的几何性质和图性变换的几何性质来命题。通常是结合图形,借助交点和关键点的坐标及图形的几何特征列方程求解。
练习三
9.(2023·广西·统考一模)如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以为边,在第一象限内作矩形,且.将矩形翻折,使点B与原点O重合,折痕为,点C的对应点落在第四象限,过点M的反比例函数的图象恰好过的中点E,则点E的坐标为___________.
【答案】
【详解】解:如图,连接,过作于,
过作于,
由折叠的性质与矩形的性质可知,,,,
∵,,
∴,
∴,
∵为中点,即,
∴,即是线段的中点,
∴是的中位线,
∴,
令,则点坐标为,点坐标为,
∵均为反比例函数上的点,
∴,
解得,
∴点坐标为,
∴,
在中,由勾股定理得,即,
解得,
∵,
解得,
则,
∴点坐标为,故答案为:.
10.(2021·江苏无锡·统考二模)如图,在中,,,与轴交于点,,点在反比例函数的图象上,且轴平分,求_____.
【答案】
【详解】解:过A作AE⊥x轴,垂足为E,
∵C(0,-4),
∴OC=4,
∵∠AED=∠COD=90°,∠ADE=∠CDO
∴△ADE∽△CDO,
,
∴AE=1;
又∵y轴平分∠ACB,CO⊥BD,
∴BO=OD,
∵∠ABC=90°,
∴∠OCD=∠DAE=∠ABE=∠BCE,
∵∠DOC=∠ADE=90°
∴△ABE~△COD,
∴
设DE=n,则BO=OD=4n,BE=9n,
∴,
∴,
∴OE=5n=,
故点A(,1),∴k=×1=故答案为:.
11.(2023·江苏苏州·统考一模)如图,在平面直角坐标系中,菱形的边经过原点,,且顶点、、都在反比例函数的图像上,则顶点的坐标为______.
【答案】
【详解】解:如图所示,过点A作轴于N,
过点C作轴于M,连接,
设,则由对称性可知,
∴,
∵四边形是菱形,
∴,
又∵,∴是等边三角形,
∴,
∵轴,轴,
∴,∴,∴,
∴,∴,
∴,∴,
∵四边形是菱形,
∴点B平移到点A和点C平移到到点D的平移方式相同,
∴点D的坐标为,
又∵点D在反比例函数图象上,∴,
∴,∴,∴,
解得(负值舍去),∴,故答案为:.
12.(2020·湖南长沙·校联考二模)如图,点A,B分别在反比例函数y=(x<0)与y=(x>0)的图象上,且△OAB是等边三角形,则点A的坐标为_____.
【答案】(1﹣,﹣﹣1)
【详解】解:延长AB到C,使得BC=AB,连接OC,
作AM⊥x轴于M,CN⊥x轴于N.设A(m,).
∵△OAB是等边三角形,
∴OB=BA=BC,
∴∠AOC=90°,
∵∠OAC=60°,
∴∠ACO=30°,
∴OC=OA,
∵∠AMO=∠AOC=∠CNO=90°,
∴∠AOM+∠MAO=90°,∠AOM+∠CON=90°,
∴∠OAM=∠CON,
∴△AMO∽△ONC,
∴===,
∵OM=﹣m,AM=﹣,
∴ON=﹣,CN=﹣m,
∴C(﹣, m),
∴B(,),
∵点B在y=﹣上,
∴×=﹣4,
整理得:m4+4m2﹣4=0,
解得:m=1﹣(不合题意的根已经舍弃),
∴A(1﹣,﹣﹣1).
故答案为:(1﹣,﹣﹣1).
① ② ③ ④
同课章节目录
