中考备考攻坚课程第五讲:压轴题难点突破1:利用平行线解决二次函数中的面积问题(教学设计,PDF版)
文档属性
| 名称 | 中考备考攻坚课程第五讲:压轴题难点突破1:利用平行线解决二次函数中的面积问题(教学设计,PDF版) |  | |
| 格式 | |||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-23 11:28:23 | ||
图片预览




文档简介
第五讲 中考压轴题难点突破 1
《利用平行线解决二次函数中的面积问题》---郭爱玲
一、考点和知识技能梳理:
二次函数中的面积问题常常出现在中考的压轴题中,是中考压轴题的难点之一。这类题
型一般综合性较强,主要考查学生的综合分析问题、解决问题能力,考察学生数形结合思想,
分类讨论思想、转化思想等。热点考题是:面积最值问题,用代数式表示面积问题,面积之
间的和、差、比值等问题。常见的解题方法有:1、设关键点坐标,利用三角形面积公式解
决问题;2、利用铅垂高、水平宽解决问题;3、利用割补法解决问题;4、利用三角形相似
解决问题; 5、 利用平行线解决问题等。其中,利用平行线解决二次函数中的面积问题的
方法常常可以做到简化问题,简便运算的作用。本节课主要学习: 利用平行线解决面积最
值问题;利用平行线转移三角形面积;利用平行线把面积比转化为线段比。
二、学习过程:
模块一
(一)知识铺垫 1:任何两条夹在平行线间的垂线段长度相等;
(1)如图 1,若直线 a∥b,则有 MN=PQ
(2)如图 2,直线 a∥b,则 S△ABC= S△BCD
(二)典例精讲:
例题 1. 已知:如图,抛物线 y=x2+4x+3 交 x 轴于 E、F 两点,交 y 轴于 A 点,若 Q 为抛
物线上一点,连接 QE,QA,设点 Q 的横坐标为 t(t<﹣3),△QAE 的面积为 S,求 S
与 t 函数关系式;
第 1 页(共 23 页)
【解答】解: 易得 A(0,3),E(-3,0),AE: y=x+3.
作 QH//AE, 交 y 轴于点 H,
S AEQ S AEH
设 Q(t,t2+4t+3),设 HQ:y=x+b
把 Q 点坐标代入 y=x+b
2
可得 HQ: y=x t 3t 3
2
∴H(0 , t 3t 3
2
), AH= t 3t ,
1
S AEQ S AEH AH OE
2
1
(t 2
3 9
3t) 3 t 2 t
2 2 2
小结:利用平行线转移面积,常常是过动点作定直线的平行线,利用“任何两条夹在平行
线间的垂线段长度相等”,把三角形转化为有一条边在坐标轴上的三角形,从而达到简
化问题的目的。
例题 2. 如图,抛物线 y=﹣x2+2x+3 交 x 轴于点 A,B,交 y 轴正半轴于点 C,连接 BC.如
图,过点 A 作 AD∥BC,交抛物线于点 D,点 P 为直线 BC 上方抛物线上任意一点,连接
DP,与 BC 交于点 E,连接 AE,AP,当△APE 面积最大时,求点 P 的坐标及△APE 面积的
最大值;
第 2 页(共 23 页)
【解答】
解法 1:解:易得 A(-1,0),B(3, 0)D(4, -5)
作∵PQ∥AD,交 x 轴于点 Q
∴S△DAP=S△QAD,S△EAD=S△BAD,
∴S△APE=S△DAP﹣S△EAD=S△QAD﹣S△BAD= S△QBD,
设点 P(m,﹣m2+2m+3),
∵PQ∥AD
∴直线 PQ 的表达式为:y=﹣x ﹣m2+3m+3,
∴Q(﹣m2+3m+3,0)
S△QBD= QB |yD|
5
= (﹣m2+3m+3)
2
=﹣ (m﹣ )2+ ≤ ,
故 S△APE 有最大值为 ,此时,点 P( , );
解法 2: 解:易得 A(-1,0),B(3, 0)D(4, -5)
过点 D 作 DF∥AP 交 x 轴于点 F,连接 PF,
∵DF∥AP, ∴S△DAP=S△FAP,
∵BC∥AD,∴S△EAD=S△BAD,
∴S△APE=S△DAP﹣S△EAD=S△FAP﹣S△BAD,
设点 P(m,﹣m2+2m+3),
直线 AP 的表达式为:y=(3﹣m)(x+1),
∵DF∥AP,则直线 FD 的表达式为:y=(3﹣m)(x﹣4)
﹣5,
令 y=(3﹣m)(x﹣4)﹣5,则 x= ,则 AF=5+ ,
则 S△APE=S△FAP﹣S△BAD= FA yP﹣ AB |yD|
= (5+ )×(﹣m2+2m+3)﹣ 4×5
=﹣ (m﹣ )2+ ≤ ,
第 3 页(共 23 页)
故 S△APE 有最大值为 ,此时,点 P( , );
解法 3:解:易得 A(-1,0),B(3, 0)D(4, -5)
设 P(t,﹣t 2+2 t +3),
直线 AD 的表达式为:y=-x﹣1
∴Q(t,﹣t -1) ∴PQ=﹣t 2+3 t +4
S△APE=S△DAP﹣S△EAD=S△DAP﹣S△BAD
= PQ ( xD xA )﹣ AB |yD|
= 5×(﹣t 2+3 t +4)﹣ 4×5
=﹣ (m﹣ )2+ ≤ ,
故 S△APE 有最大值为 ,此时,点 P( , );
小结:△APE 中,P、E 都是动点,只有一个定点 A,如果过三角形的某个点构造平行线,
在表达三边所在直线的解析式上运算量相对较大,所以不建议直接构造平行线转移△
APE,而是采用割补法把△APE 转移为△APD 的面积减去△AED 的面积,因为 BC//AD,
所以△AED 可以转移为△ABD 的面积,A、B、D 都是定点,面积可求,所以只需要表示
△APD 的面积,问题即可解决。A 和 D 为定点,P 为动点,可考虑构造平行线表示面积,
也可以考虑铅垂高水平宽求面积。
(三) 跟进练习:
1. 如图,已知二次函数 y=﹣ x2+ x+4 的图象与 y 轴交于点 A(0,4).与 x 轴交于点
B,C,点 C 坐标为(8,0),连接 AB、AC.若点 N 在线段 BC 上运动(不与点 B,C 重
合),过点 N 作 NM∥AC,交 AB 于点 M,当△AMN 面积最大时,求此时点 N 的坐标;
第 4 页(共 23 页)
【解答】
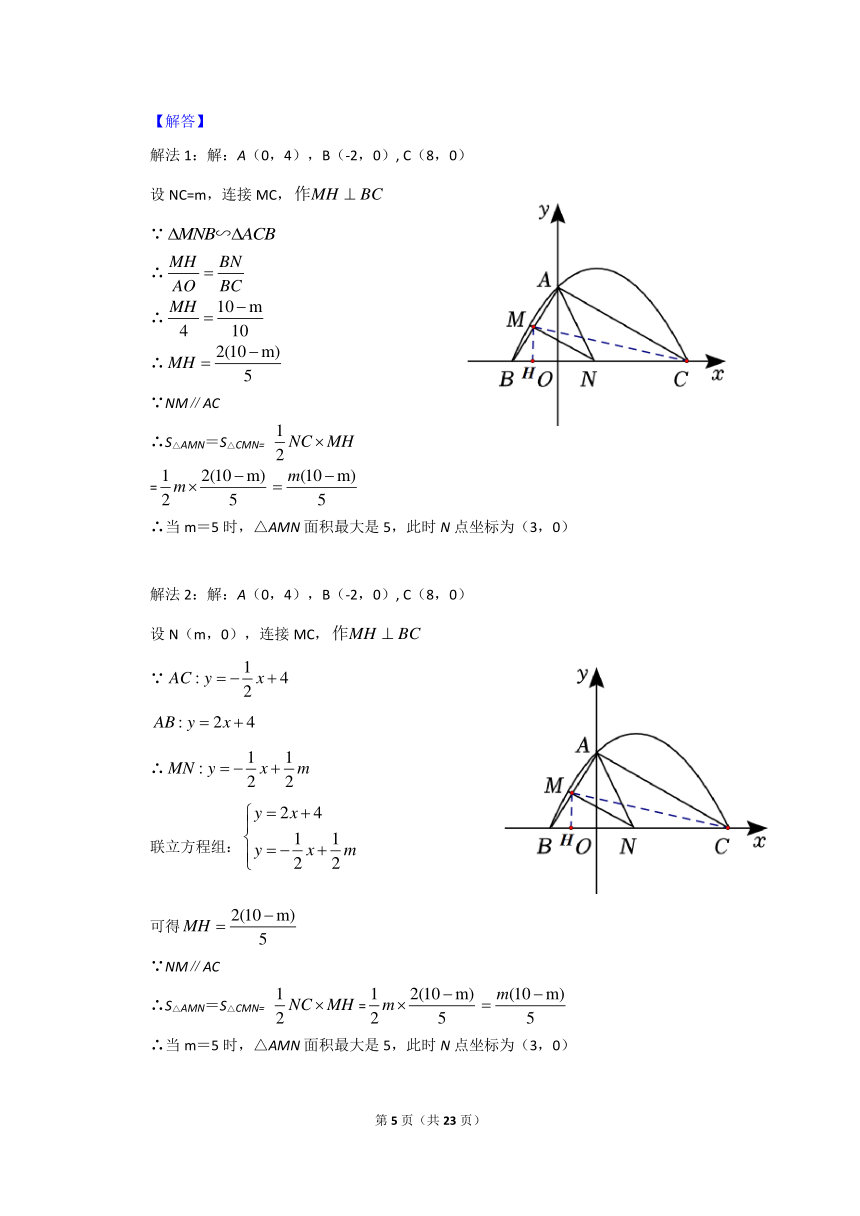
解法 1:解:A(0,4),B(-2,0), C(8,0)
设 NC=m,连接 MC,作MH BC
∵ MNB∽ ACB
MH BN
∴
AO BC
MH 10 m
∴
4 10
2(10 m)
∴MH
5
∵NM∥AC
1
∴S△AMN=S△CMN= NC MH
2
1 2(10 m) m(10 m)
= m
2 5 5
∴当 m=5 时,△AMN 面积最大是 5,此时 N 点坐标为(3,0)
解法 2:解:A(0,4),B(-2,0), C(8,0)
设 N(m,0),连接 MC,作MH BC
1
∵ AC : y x 4
2
AB : y 2x 4
1 1
∴MN : y x m
2 2
y 2x 4
1 1
联立方程组: y x m
2 2
2(10 m)
可得MH
5
∵NM∥AC
1 1 2(10 m) m(10 m)
∴S△AMN=S△CMN= NC MH = m
2 2 5 5
∴当 m=5 时,△AMN 面积最大是 5,此时 N 点坐标为(3,0)
第 5 页(共 23 页)
2.如图,在平面直角坐标系中,抛物线 y= x2+x﹣ 与 x 轴交于 A、B,与 y 轴交于点 C,
点 D(2,n)在抛物线上.过 B 作 BE∥AD 交抛物线于点 E,P 为直线 BE 下方抛物线上一
点,连接 PD 交直线 BE 于点 F,连接 AE、AF,求四边形 AEPF 的面积最大值,并求出此
时点 P 的坐标.
【解答】解:易得 A(﹣3,0),B(1,0)
∵D 点在抛物线上,∴n= , ∴D(2, ),
∴y= x+ ,
∵BE∥AD,∴ S AEF S DEF
∴ S S PEF S DEF S 四边形AEPF PED
∴直线 BE 的解析式为 y= x﹣ ,
令 x2+x﹣ = x﹣ ,解得 x=1 或 x=﹣2,
∴E(﹣2,﹣ ),
作 PH x轴,交DE于点H ,设 P(t, t2+t﹣ ),
∴DE:y=x+
∴H (t, t+ )
1 1 3 1
PH (t+ ) ( t2 t ) t2∴ 2
2 2 2 2
S S
四边形AEPF PEF
S DEF S PED
1 1 1
(x 2D xE ) PH 4 ( t 2) t
2 4
2 2 2
∴当 t=0 时,四边形 AEPF 的面积最大,最大值为 4,此时 P(0,﹣ );
第 6 页(共 23 页)
模块二
(一)典例精讲:
1 2
例题 1. 如图,在平面直角坐标系内抛物线 y= x x 4与 x 轴交于点 A,点 B,与 y 轴交
2
于点 C.过点 A 的直线 y=x+2 与抛物线交于点 E.点 P 为第四象限内抛物线上的一个动
点.在点 P 的运动过程中,是否存在点 P 使得△AEP 的面积最大,若存在,请求出点 P
的坐标.
【解答】解:存在点 P 使得△AEP 的面积最大,理由如下:
联立方程组 ,解得 或 ,∴E(6,8),
在直线 AE 的下方作 MN//AE,
当 MN 与抛物线有唯一交点 P 时,此时△AEP 的面积最大,P 为所求的点
设 MN: y=x b
y x b
联立方程组 1 2
y x x 4
2
1
可得 x
2 2x 4 b 0
2
1
4 4 ( 4 b) 0 解得b 6
2
y x 6
联立方程组 1
y x
2 3x 8
2
可得 P(2,﹣4).此时 S△APE=32,
小结:△APE 中,A 和 E 是定点,AE 长是定值,当 P 点到直线 AE 的距离最大时,△APE
面积最大。所以,当过 P 点且平行于 AE 的直线与抛物线有唯一交点时,这个唯一的交
点就是所求的点。
第 7 页(共 23 页)
例题 2. 如图,抛物线 y=﹣ x2+3x+8 与 x 轴交于点 A、B 点,与 y 轴交于点 C 点,P 是抛物
S 3
线上第一象限上的动点,连接 PB,PC,当 PBC 时,求点 P 的坐标.
S ABC 5
【解答】
解:易得 A(-2,0),B(8,0), C(0,8)
作 AD//BC,交 y 轴于 D,
易求 BC:y=﹣x+8
AD:y=﹣x-2,
∴CD=10,
在 C 点上方截取 CE=6,过 E 作 EP//BC,交抛物线于点 P,
则 P 为所求的点
PQ:y=﹣x+14,
y x 14
联立方程组, 1
y x2 3x 8
2
可得点 P 的坐标为(2,12)或 P(6,8)
小结;同底三角形面积比等于这条底边上的高的比,所以同底三角形面积比转化为线段比,
通过构造平行线,把高的比转化为 y 轴上的两段线段的比。
第 8 页(共 23 页)
(二) 跟进练习
2
1.如图,已知抛物线 y x 2x 3与 x 轴交于 A、B 两点,与 y 轴交于点 C.点 P 是第四
象限内抛物线上的一个动点,当四边形 ABPC 的面积最大时,求点 P 的坐标.
【解答】解:A(﹣2,0),B(4,0)C(0,-4)
连接 BC,过点 P 作 MN∥BC,当 MN 与抛物线有唯一交点 P 时,△PBC 的面积最大,此
时四边形 ABPC 的面积=S△ABC+S△PBC 取得最大面积,P 为所求的点。
由点 B、C 的坐标得,直线 BC 的表达式为:y=x﹣3,
设 MN: y x b
y x b
联立方程组
y x
2 2x 3
可得 x
2 3x 3 b 0
9 4 ( 3 b) 0
21
解得b
4
21
y x 3 15
联立方程组 4 可得P( ,- ).
2 4
y x
2 2x 3
则四边形 ABPC 的面积=S△ABC+S△PBC=6
3 15
故当P( ,- ),四边形 ABPC 的面积最大.
2 4
第 9 页(共 23 页)
2.如图,抛物线 y x2 2x 3的顶点坐标为点 C(1,4),交 x 轴于点 A(3,0),交
9
y 轴于点 B(0,3). 抛物线上第一象限内是否存在一动点 P,使 S△PAB= △CAB ,若存在,
8
求出 P 点的坐标;若不存在,请说明理由。
【解答】解:易得 AB:y=﹣x+3
作 CD//AB,交 y 轴于 D,可得 CD:y=﹣x+5
9
∴BD=2,在 B 点上方截取 BG= ,
4
过 G 作 GH//AB,交抛物线于点 P1, P2 ,
则 P1,P2 ,即为所求的点
21
GH:y=﹣x+ ,
4
21
y x
联立方程组, 4
2
y x 2x 3
3 15
可得点 P 的坐标为 P( , )
2 4
第 10 页(共 23 页)
3.如图,抛物线 y=﹣x2+2x+3 经过 A(﹣1,0)、B(3,0)、C(0,3)三点,对称轴
与抛物线相交于点 P、与 BC 相交于点 E,连接 PB.抛物线上是否存在一点 Q,使△QPB
与△EPB 的面积相等,若存在,请求出点 Q 的坐标;若不存在,说明理由.
【解答】解:存在,理由:
由 y=﹣x2+2x+3=﹣(x﹣1)2+4,
则顶点 P(1,4),对称轴为直线 x=1,
∴H(1,0),
∴PH=4,BH=2,
∵B(3,0),C(0,3),
∴直线 BC 解析式为 y=﹣x+3,
∴点 E(1,2),
如图,过点 E 作 EQ∥BC,交抛物线于 Q,此时△QPB 与△PEB 的面积相等,
由点 P、B 的坐标得,直线 PB 的表达式为:y=﹣2(x﹣3),
则直线 QE 的表达式为:y=﹣2(x﹣1)+2②,
联立①②并整理得:x2﹣4x+1=0,
解得:x=2 ,
则点 Q 的坐标为(2﹣ ,2 )或(2+ ,﹣2 );
对于直线 QE,设 QE 交 x 轴于点 R,
令 y=﹣2(x﹣1)+2=0,
解得:x=2,即点 R(2,0),
则 BR=3﹣2=1,
取点 R′使 BR=BR′,过点 R′作 PB 的平行线 l,如上图,则点 R′(4,0),
则直线 l 的表达式为:y=﹣2(x﹣4),
联立 y=﹣x2+2x+3 和 y=﹣2(x﹣4)得:x2﹣4x+5=0,
第 11 页(共 23 页)
则Δ=16﹣20<0,无解,
故在点 B 的右侧不存在点 Q,
综上,点 Q 的坐标为(2﹣ ,2 )或(2+ ,﹣2 );
4.如图所示抛物线 y= (x﹣3)2﹣6;与 x 轴交于 O,A 两点,OA=6,点 P 在抛物线上,
过点 P 的直线 y=x+m 与抛物线的对称轴交于点 Q.当△POQ 与△PAQ 的面积之比为 1:
3 时,求 m 的值.
【解答】解:设 PQ 与 y 轴交于点 H,作 OM//PQ,
作 AG//PQ,交 y 轴于点 G
易得 AG:y=x-6 ,OM:y=x
∴OG=6,OH m
∵△POQ 与△PAQ 的面积之比为 1:3,
OH m 1
如图 1,
HG m 6 3
解得 m=3
OH m 1
如图 2,
HG 6 m 3
解得 m=﹣ ∴m=﹣ 或 m=3.
第 12 页(共 23 页)
模块三
(一)典例精讲:
例题 1.如图,抛物线 y=x2﹣4x 与 x 轴相交于另一点 A.在第一象限内与直线 y=x 交于点
B,点 E 是点 B 关于抛物线对称轴的对称点,点 F 是直线 OB 下方的抛物线上的动点,EF
与直线 OB 交于点 G.设△BFG 和△BEG 的面积分别为 S1 和 S2,求 的最大值.
【解答】
解:如图 2,过点 F 作 FW∥x 轴交直线 OB 于点 W,
设 F(t,t2﹣4t),则 W 的纵坐标为 t2﹣4t,
∵直线 OB 的解析式为 y=x,
∴W(t2﹣4t,t2﹣4t),
∴WF=t﹣(t2﹣4t)=﹣t2+5t,
∵易得 B(5,5),点 E、B 关于抛物线对称轴直线 x=2 对称,
∴BE∥x 轴,BE=6,
∴BE∥WF,
∴△WFG∽△BEG,
∴ = = ,
∵ = = = =﹣ (t﹣ )2+ ,
∴当 t= 时, 的最大值为 .
第 13 页(共 23 页)
例题 2. 已知抛物线 y=﹣x2+2x+3 经过 A、B 两点.P 是抛物线上一点,且在直线 BC 的
上方.连结 AC、AP,AP 交 BC 于点 M,作 PH∥AC 交 BC 于点 H.记△PHM,△PMC,
△CAM 的面积分别为 S1,S2,S3.判断 是否存在最大值.若存在,求出最大值;
若不存在,请说明理由.
【解答】
解法 1 解: 存在最大值,理由如下:
易得 A(﹣1,0),B(3,0)
作 AR∥y 轴交 BC 于 R,过 P 作作 PQ⊥BC 交 BC 于 Q,
由直线 BC 解析式为 y=﹣x+3, A(﹣1,0),
∴R(﹣1,4),
∴AR=4
设 P(t,﹣t2+2t+3),
则 Q(t,﹣t+3),
∴PQ=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t,
∵PH∥AC,易证△PMH∽△AMC,
∴ = = ,
∴ , ,
第 14 页(共 23 页)
∴ ,
∵AR∥PQ,AC∥PH,
可得△ACR∽△PHQ,
PH PQ
∴ = ,
AC AR
S
∴ 1
S 2PH
2 = =﹣ (t﹣ )2+ ,
S2 S3 AC
∴当 t= 时, + 取最大值,最大值为 .
解法 2 解: 存在最大值,理由如下:
易得 A(﹣1,0),B(3,0)
作 AR∥BC 交 y 轴于 R,过 P 作作 PQ⊥BC 交 BC 于 Q,
由直线 BC 解析式为 y=﹣x+3,易得直线 AR 解析式为 y=﹣x﹣1,
令 x=0 得 y=﹣1,∴R(0,﹣1),
∵C(0,3),∴CR=4,
设 P(t,﹣t2+2t+3),则 Q(t,﹣t+3),
∴PQ=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t,
∵PH∥AC,易证△PMH∽△AMC,∴ = = ,
∴ , ,
∴ ,
∵AR∥BC,PH∥AC, PQ∥CR,
可得△ACR∽△HPQ,
PH PQ
∴ = ,
AC CR
S1 S2 2PH∴ = =﹣ (t﹣ )2+ ,
S2 S3 AC
第 15 页(共 23 页)
∴当 t= 时, + 取最大值,最大值为 .
小结:同高三角形面积比等于对应底边的比,可利用平行线把底边比转化为水平线段比
或铅垂线段比。具体到本题,因为 AC 长度是定值,所以表示面积比也可以作 PQ∥y 轴,
直接用含 t 的代数式表示 PQ
(二)跟进练习:
1. 抛物线 y=﹣ ,与 x 轴分别交于 A,B 两点(点 A 在点 B 的左侧),与 y 轴
交于点 C(0,3),抛物线对称轴为 x=1,点 P 是第一象限抛物线上动点,连接 BC,PB.如
图 1,连接 PA,交 BC 于点 M,设△ABM 的面积为 S1,
△PBM 的面积为 S2,求 的最小值及此时点 P 的坐标;
【解答】解:如图,作 PQ∥AB,交 BC 于 Q,
∴△PMQ∽△AMB, ∴ ,
设 P(m,﹣ ),
由﹣ 得,
x= ,
∴PQ=m﹣( )=﹣ +2m,
∵AB=4﹣(﹣2)=6,
第 16 页(共 23 页)
∴ = = ,
∴当 m=2 时,﹣ 的最大值为 2,
∴ 的最小值为 3,
当 m=2 时,y=3, ∴P(2,3);
2. 抛物线 y=﹣ x2+ x+3 与 y 轴交于点 C,与 x 轴交于 A、
B 两点(点 A 在点 B 的左侧),其中 A(﹣ ,0),点 D
为直线 BC 上方抛物线上一点,连接 AD、BC 交于点 E,连
接 BD,记△BDE 的面积为 S1,△ABE 的面积为 S2,求 的
最大值.
【解答】解: 过点 D 作 DG⊥x 轴于点 G,交 BC 于点 F,过点
A 作 AK⊥x 轴交 BC 的延长线于点 K,
∴△DEF∽△AEK,
∴ = ,
∵C(0,3),B(3 ,0),
∴直线 BC 的解析式为:y=﹣ x+3;
设点 D 的横坐标为 t,∴D(t,﹣ t2+ t+3),
∴F(t,﹣ t+3),K(﹣ ,4),
∴AF=4,DF=﹣ t2+ t+3﹣(﹣ t+3)=﹣ t2+ t;
∴ = =﹣ t2+ t=﹣ (t﹣ )2+ ,
第 17 页(共 23 页)
∴当 t= 时, 的最大值为 .
3 2 9
3. 如图,在平面直角坐标系中,抛物线 y x x 3与 x 轴交于点 A(4,0),C(﹣
4 4
1,0)与 y 轴交于点 B, 点 Q 为直线 AB 上方抛物线上一点,
OQ 交 AB 于点 D,QE∥BO 交 AB 于点 E.记△QDE,△QDB,
△BDO 的面积分别为 S1,S2,S3.求 的最大值.
【解答】解:设直线 AB 的解析式为 .
∵4E∥BO,易证△DQE∽△DOB,
∴ ,∴ , ,
∴ .
设 Q 点坐标为 ,则点 E 坐标为 ,
∴ ,
∴当 x=2 时,QE 最大为 3,即 的最大值为 2.
第 18 页(共 23 页)
4. 如图,在平面直角坐标系中,二次函数 y x2 6x 5的图象与 x 轴交于 A、B 两点,
与 y 轴交于点 C,其顶点为 P,连接 PA、 AC 、CP,过点 C 作 y 轴的垂线 l.直线 l上
是否存在点 Q,使△PBQ 的面积等于△PAC 的面积的 2 倍?若存在,求出点 Q 的坐标;
若不存在,请说明理由.
【解答】解:设 PC 与 x 轴交于 E 点,PQ 与坐标轴交于 F 点
1
AE PH
S
∵ MNB 2
AE
S 1 PBQ BFBF PH
2
根据解析式,可得 A(1,0),P(3,4),C(0,-5) B(5,0)
5
∴PC 解析式为: y=3x 5 可得 E( ,0)
3
2
∴AE=
3
4 11 19
∴BF= ∴F( ,0)或 F( ,0)
3 3 3
6 38
∴PF 解析式为: y=-6x 22 或 y=- x
5 5
27 21
当 y=-5 时,可求得 Q( ,-5)或 F( ,-5)
6 2
第 19 页(共 23 页)
5.如图 1,二次函数 y=x2﹣3x﹣4 的图象与 x 轴交于点 A、B 两点,与 y 轴交于点 C,直线
BC 的函数表达式为 y=x﹣4,直线 x=1 与 x 轴交于点 D,P 为直线 x=1 上一动点,连接
PB,将 PB 绕 P 顺时针旋转一定角度得到 PQ.若点 Q 恰好落在抛物线位于第四象限的图
象上,连接 AQ 交 BC 于点 E,连接 AC,CQ,当△CEQ 与△ACE 的面积之比最大时,求点
P 的坐标;
【解答】解: 如图 1,作 AM⊥x 轴交直线 BC 于点 M,作 QN⊥x 轴交直线 BC 于点 N,
则 AM∥QN,
∴△QEN∽△AEM,
∴ = = ,
直线 y=x﹣4,当 x=﹣1 时,y=﹣5,
∴M(﹣1,﹣5),
∴AM=5,
设 Q(m,m2﹣3m﹣4),则 N(m,m﹣4),
∴QN=m﹣4﹣(m2﹣3m﹣4)=﹣m2+4m,
∴ = =﹣ (m﹣2)2+ ,
∴当 m=2 时,△CEQ 与△ACE 的面积之比最大,此时 Q(2,﹣6),
设 P(1,n),
由旋转得 PQ=PB,
∴(1﹣2)2+(n+6)2=(4﹣1)2+(0﹣n)2,
解得 n=﹣ ,∴P(1,﹣ ).
第 20 页(共 23 页)
6.在平面直角坐标系中 xOy 中,二次函数 y=﹣x2+x+2 的图象与 x 轴交于点 A、B,与 y 轴
交于点 C.若点 P 是二次函数图象上位于线段 BC 上方的一个动点.如图,连接 AC,CP,
AP,AP交 BC于点 E,过点 P作AC的平行线交 BC于点Q,将△PEQ与△PCE的面积比
记为 a,将△PCE 与△ACE 的面积比 记为 b,当 a+ b 有最大值时,求点 P 的坐
标;
【解答】解:)①令 x=0,则 y=2,
∴C(0,2),
∴OC=2.
∵A(﹣1,0)、B(2,0),
∴OA=1,OB=2,
∴OB=OC,
∴∠OBC=∠OCB=45°.
过点 P 作 PF⊥x 轴于点 F,交 BC 于点 G,过点 Q 作 QH
⊥PF 于点 H,如图,
设 P(m,﹣m2+m+2),则 OF=m,PF=﹣m2+m+2,
∴BF=OB﹣OF=2﹣m,
∵△GFB 为等腰直角三角形,
∴GF=BF=2﹣m,
∴PG=PF﹣GF=﹣m2+2m.
∵OA=1,OC=2,∴AC= = .
∵AC∥PQ,PF∥OC,
第 21 页(共 23 页)
∴∠ACO=∠FPQ.
∵∠OAC=∠QHP=90°,
∴△OAC∽△HQP,
∴ .
设 QH=n,
∴ ,
∴PH=2n,PQ= n.
∵QH∥OB,
∴∠HQB=∠OBC=45°,
∴△QHG 为等腰直角三角形,
∴GH=QH=n,
∴PG=PH+HG=3n,
∴ ,
∴PQ= (﹣m2+2m).
∵PQ∥AC,∴△PQE∽△ACE,
∴ .
∵等高的三角形的面积比等于底的比,
∴ =a= , =b= ,
∴a=b= = (﹣m2+2m)=﹣ + m.
∴a+ b=(1+ )a=﹣( )(m﹣1)2+ ,
∵﹣( )<0,
∴当 m=1 时,a+ b 有最大值,
∴点 P 的坐标(1,1);
第 22 页(共 23 页)
第 23 页(共 23 页)
《利用平行线解决二次函数中的面积问题》---郭爱玲
一、考点和知识技能梳理:
二次函数中的面积问题常常出现在中考的压轴题中,是中考压轴题的难点之一。这类题
型一般综合性较强,主要考查学生的综合分析问题、解决问题能力,考察学生数形结合思想,
分类讨论思想、转化思想等。热点考题是:面积最值问题,用代数式表示面积问题,面积之
间的和、差、比值等问题。常见的解题方法有:1、设关键点坐标,利用三角形面积公式解
决问题;2、利用铅垂高、水平宽解决问题;3、利用割补法解决问题;4、利用三角形相似
解决问题; 5、 利用平行线解决问题等。其中,利用平行线解决二次函数中的面积问题的
方法常常可以做到简化问题,简便运算的作用。本节课主要学习: 利用平行线解决面积最
值问题;利用平行线转移三角形面积;利用平行线把面积比转化为线段比。
二、学习过程:
模块一
(一)知识铺垫 1:任何两条夹在平行线间的垂线段长度相等;
(1)如图 1,若直线 a∥b,则有 MN=PQ
(2)如图 2,直线 a∥b,则 S△ABC= S△BCD
(二)典例精讲:
例题 1. 已知:如图,抛物线 y=x2+4x+3 交 x 轴于 E、F 两点,交 y 轴于 A 点,若 Q 为抛
物线上一点,连接 QE,QA,设点 Q 的横坐标为 t(t<﹣3),△QAE 的面积为 S,求 S
与 t 函数关系式;
第 1 页(共 23 页)
【解答】解: 易得 A(0,3),E(-3,0),AE: y=x+3.
作 QH//AE, 交 y 轴于点 H,
S AEQ S AEH
设 Q(t,t2+4t+3),设 HQ:y=x+b
把 Q 点坐标代入 y=x+b
2
可得 HQ: y=x t 3t 3
2
∴H(0 , t 3t 3
2
), AH= t 3t ,
1
S AEQ S AEH AH OE
2
1
(t 2
3 9
3t) 3 t 2 t
2 2 2
小结:利用平行线转移面积,常常是过动点作定直线的平行线,利用“任何两条夹在平行
线间的垂线段长度相等”,把三角形转化为有一条边在坐标轴上的三角形,从而达到简
化问题的目的。
例题 2. 如图,抛物线 y=﹣x2+2x+3 交 x 轴于点 A,B,交 y 轴正半轴于点 C,连接 BC.如
图,过点 A 作 AD∥BC,交抛物线于点 D,点 P 为直线 BC 上方抛物线上任意一点,连接
DP,与 BC 交于点 E,连接 AE,AP,当△APE 面积最大时,求点 P 的坐标及△APE 面积的
最大值;
第 2 页(共 23 页)
【解答】
解法 1:解:易得 A(-1,0),B(3, 0)D(4, -5)
作∵PQ∥AD,交 x 轴于点 Q
∴S△DAP=S△QAD,S△EAD=S△BAD,
∴S△APE=S△DAP﹣S△EAD=S△QAD﹣S△BAD= S△QBD,
设点 P(m,﹣m2+2m+3),
∵PQ∥AD
∴直线 PQ 的表达式为:y=﹣x ﹣m2+3m+3,
∴Q(﹣m2+3m+3,0)
S△QBD= QB |yD|
5
= (﹣m2+3m+3)
2
=﹣ (m﹣ )2+ ≤ ,
故 S△APE 有最大值为 ,此时,点 P( , );
解法 2: 解:易得 A(-1,0),B(3, 0)D(4, -5)
过点 D 作 DF∥AP 交 x 轴于点 F,连接 PF,
∵DF∥AP, ∴S△DAP=S△FAP,
∵BC∥AD,∴S△EAD=S△BAD,
∴S△APE=S△DAP﹣S△EAD=S△FAP﹣S△BAD,
设点 P(m,﹣m2+2m+3),
直线 AP 的表达式为:y=(3﹣m)(x+1),
∵DF∥AP,则直线 FD 的表达式为:y=(3﹣m)(x﹣4)
﹣5,
令 y=(3﹣m)(x﹣4)﹣5,则 x= ,则 AF=5+ ,
则 S△APE=S△FAP﹣S△BAD= FA yP﹣ AB |yD|
= (5+ )×(﹣m2+2m+3)﹣ 4×5
=﹣ (m﹣ )2+ ≤ ,
第 3 页(共 23 页)
故 S△APE 有最大值为 ,此时,点 P( , );
解法 3:解:易得 A(-1,0),B(3, 0)D(4, -5)
设 P(t,﹣t 2+2 t +3),
直线 AD 的表达式为:y=-x﹣1
∴Q(t,﹣t -1) ∴PQ=﹣t 2+3 t +4
S△APE=S△DAP﹣S△EAD=S△DAP﹣S△BAD
= PQ ( xD xA )﹣ AB |yD|
= 5×(﹣t 2+3 t +4)﹣ 4×5
=﹣ (m﹣ )2+ ≤ ,
故 S△APE 有最大值为 ,此时,点 P( , );
小结:△APE 中,P、E 都是动点,只有一个定点 A,如果过三角形的某个点构造平行线,
在表达三边所在直线的解析式上运算量相对较大,所以不建议直接构造平行线转移△
APE,而是采用割补法把△APE 转移为△APD 的面积减去△AED 的面积,因为 BC//AD,
所以△AED 可以转移为△ABD 的面积,A、B、D 都是定点,面积可求,所以只需要表示
△APD 的面积,问题即可解决。A 和 D 为定点,P 为动点,可考虑构造平行线表示面积,
也可以考虑铅垂高水平宽求面积。
(三) 跟进练习:
1. 如图,已知二次函数 y=﹣ x2+ x+4 的图象与 y 轴交于点 A(0,4).与 x 轴交于点
B,C,点 C 坐标为(8,0),连接 AB、AC.若点 N 在线段 BC 上运动(不与点 B,C 重
合),过点 N 作 NM∥AC,交 AB 于点 M,当△AMN 面积最大时,求此时点 N 的坐标;
第 4 页(共 23 页)
【解答】
解法 1:解:A(0,4),B(-2,0), C(8,0)
设 NC=m,连接 MC,作MH BC
∵ MNB∽ ACB
MH BN
∴
AO BC
MH 10 m
∴
4 10
2(10 m)
∴MH
5
∵NM∥AC
1
∴S△AMN=S△CMN= NC MH
2
1 2(10 m) m(10 m)
= m
2 5 5
∴当 m=5 时,△AMN 面积最大是 5,此时 N 点坐标为(3,0)
解法 2:解:A(0,4),B(-2,0), C(8,0)
设 N(m,0),连接 MC,作MH BC
1
∵ AC : y x 4
2
AB : y 2x 4
1 1
∴MN : y x m
2 2
y 2x 4
1 1
联立方程组: y x m
2 2
2(10 m)
可得MH
5
∵NM∥AC
1 1 2(10 m) m(10 m)
∴S△AMN=S△CMN= NC MH = m
2 2 5 5
∴当 m=5 时,△AMN 面积最大是 5,此时 N 点坐标为(3,0)
第 5 页(共 23 页)
2.如图,在平面直角坐标系中,抛物线 y= x2+x﹣ 与 x 轴交于 A、B,与 y 轴交于点 C,
点 D(2,n)在抛物线上.过 B 作 BE∥AD 交抛物线于点 E,P 为直线 BE 下方抛物线上一
点,连接 PD 交直线 BE 于点 F,连接 AE、AF,求四边形 AEPF 的面积最大值,并求出此
时点 P 的坐标.
【解答】解:易得 A(﹣3,0),B(1,0)
∵D 点在抛物线上,∴n= , ∴D(2, ),
∴y= x+ ,
∵BE∥AD,∴ S AEF S DEF
∴ S S PEF S DEF S 四边形AEPF PED
∴直线 BE 的解析式为 y= x﹣ ,
令 x2+x﹣ = x﹣ ,解得 x=1 或 x=﹣2,
∴E(﹣2,﹣ ),
作 PH x轴,交DE于点H ,设 P(t, t2+t﹣ ),
∴DE:y=x+
∴H (t, t+ )
1 1 3 1
PH (t+ ) ( t2 t ) t2∴ 2
2 2 2 2
S S
四边形AEPF PEF
S DEF S PED
1 1 1
(x 2D xE ) PH 4 ( t 2) t
2 4
2 2 2
∴当 t=0 时,四边形 AEPF 的面积最大,最大值为 4,此时 P(0,﹣ );
第 6 页(共 23 页)
模块二
(一)典例精讲:
1 2
例题 1. 如图,在平面直角坐标系内抛物线 y= x x 4与 x 轴交于点 A,点 B,与 y 轴交
2
于点 C.过点 A 的直线 y=x+2 与抛物线交于点 E.点 P 为第四象限内抛物线上的一个动
点.在点 P 的运动过程中,是否存在点 P 使得△AEP 的面积最大,若存在,请求出点 P
的坐标.
【解答】解:存在点 P 使得△AEP 的面积最大,理由如下:
联立方程组 ,解得 或 ,∴E(6,8),
在直线 AE 的下方作 MN//AE,
当 MN 与抛物线有唯一交点 P 时,此时△AEP 的面积最大,P 为所求的点
设 MN: y=x b
y x b
联立方程组 1 2
y x x 4
2
1
可得 x
2 2x 4 b 0
2
1
4 4 ( 4 b) 0 解得b 6
2
y x 6
联立方程组 1
y x
2 3x 8
2
可得 P(2,﹣4).此时 S△APE=32,
小结:△APE 中,A 和 E 是定点,AE 长是定值,当 P 点到直线 AE 的距离最大时,△APE
面积最大。所以,当过 P 点且平行于 AE 的直线与抛物线有唯一交点时,这个唯一的交
点就是所求的点。
第 7 页(共 23 页)
例题 2. 如图,抛物线 y=﹣ x2+3x+8 与 x 轴交于点 A、B 点,与 y 轴交于点 C 点,P 是抛物
S 3
线上第一象限上的动点,连接 PB,PC,当 PBC 时,求点 P 的坐标.
S ABC 5
【解答】
解:易得 A(-2,0),B(8,0), C(0,8)
作 AD//BC,交 y 轴于 D,
易求 BC:y=﹣x+8
AD:y=﹣x-2,
∴CD=10,
在 C 点上方截取 CE=6,过 E 作 EP//BC,交抛物线于点 P,
则 P 为所求的点
PQ:y=﹣x+14,
y x 14
联立方程组, 1
y x2 3x 8
2
可得点 P 的坐标为(2,12)或 P(6,8)
小结;同底三角形面积比等于这条底边上的高的比,所以同底三角形面积比转化为线段比,
通过构造平行线,把高的比转化为 y 轴上的两段线段的比。
第 8 页(共 23 页)
(二) 跟进练习
2
1.如图,已知抛物线 y x 2x 3与 x 轴交于 A、B 两点,与 y 轴交于点 C.点 P 是第四
象限内抛物线上的一个动点,当四边形 ABPC 的面积最大时,求点 P 的坐标.
【解答】解:A(﹣2,0),B(4,0)C(0,-4)
连接 BC,过点 P 作 MN∥BC,当 MN 与抛物线有唯一交点 P 时,△PBC 的面积最大,此
时四边形 ABPC 的面积=S△ABC+S△PBC 取得最大面积,P 为所求的点。
由点 B、C 的坐标得,直线 BC 的表达式为:y=x﹣3,
设 MN: y x b
y x b
联立方程组
y x
2 2x 3
可得 x
2 3x 3 b 0
9 4 ( 3 b) 0
21
解得b
4
21
y x 3 15
联立方程组 4 可得P( ,- ).
2 4
y x
2 2x 3
则四边形 ABPC 的面积=S△ABC+S△PBC=6
3 15
故当P( ,- ),四边形 ABPC 的面积最大.
2 4
第 9 页(共 23 页)
2.如图,抛物线 y x2 2x 3的顶点坐标为点 C(1,4),交 x 轴于点 A(3,0),交
9
y 轴于点 B(0,3). 抛物线上第一象限内是否存在一动点 P,使 S△PAB= △CAB ,若存在,
8
求出 P 点的坐标;若不存在,请说明理由。
【解答】解:易得 AB:y=﹣x+3
作 CD//AB,交 y 轴于 D,可得 CD:y=﹣x+5
9
∴BD=2,在 B 点上方截取 BG= ,
4
过 G 作 GH//AB,交抛物线于点 P1, P2 ,
则 P1,P2 ,即为所求的点
21
GH:y=﹣x+ ,
4
21
y x
联立方程组, 4
2
y x 2x 3
3 15
可得点 P 的坐标为 P( , )
2 4
第 10 页(共 23 页)
3.如图,抛物线 y=﹣x2+2x+3 经过 A(﹣1,0)、B(3,0)、C(0,3)三点,对称轴
与抛物线相交于点 P、与 BC 相交于点 E,连接 PB.抛物线上是否存在一点 Q,使△QPB
与△EPB 的面积相等,若存在,请求出点 Q 的坐标;若不存在,说明理由.
【解答】解:存在,理由:
由 y=﹣x2+2x+3=﹣(x﹣1)2+4,
则顶点 P(1,4),对称轴为直线 x=1,
∴H(1,0),
∴PH=4,BH=2,
∵B(3,0),C(0,3),
∴直线 BC 解析式为 y=﹣x+3,
∴点 E(1,2),
如图,过点 E 作 EQ∥BC,交抛物线于 Q,此时△QPB 与△PEB 的面积相等,
由点 P、B 的坐标得,直线 PB 的表达式为:y=﹣2(x﹣3),
则直线 QE 的表达式为:y=﹣2(x﹣1)+2②,
联立①②并整理得:x2﹣4x+1=0,
解得:x=2 ,
则点 Q 的坐标为(2﹣ ,2 )或(2+ ,﹣2 );
对于直线 QE,设 QE 交 x 轴于点 R,
令 y=﹣2(x﹣1)+2=0,
解得:x=2,即点 R(2,0),
则 BR=3﹣2=1,
取点 R′使 BR=BR′,过点 R′作 PB 的平行线 l,如上图,则点 R′(4,0),
则直线 l 的表达式为:y=﹣2(x﹣4),
联立 y=﹣x2+2x+3 和 y=﹣2(x﹣4)得:x2﹣4x+5=0,
第 11 页(共 23 页)
则Δ=16﹣20<0,无解,
故在点 B 的右侧不存在点 Q,
综上,点 Q 的坐标为(2﹣ ,2 )或(2+ ,﹣2 );
4.如图所示抛物线 y= (x﹣3)2﹣6;与 x 轴交于 O,A 两点,OA=6,点 P 在抛物线上,
过点 P 的直线 y=x+m 与抛物线的对称轴交于点 Q.当△POQ 与△PAQ 的面积之比为 1:
3 时,求 m 的值.
【解答】解:设 PQ 与 y 轴交于点 H,作 OM//PQ,
作 AG//PQ,交 y 轴于点 G
易得 AG:y=x-6 ,OM:y=x
∴OG=6,OH m
∵△POQ 与△PAQ 的面积之比为 1:3,
OH m 1
如图 1,
HG m 6 3
解得 m=3
OH m 1
如图 2,
HG 6 m 3
解得 m=﹣ ∴m=﹣ 或 m=3.
第 12 页(共 23 页)
模块三
(一)典例精讲:
例题 1.如图,抛物线 y=x2﹣4x 与 x 轴相交于另一点 A.在第一象限内与直线 y=x 交于点
B,点 E 是点 B 关于抛物线对称轴的对称点,点 F 是直线 OB 下方的抛物线上的动点,EF
与直线 OB 交于点 G.设△BFG 和△BEG 的面积分别为 S1 和 S2,求 的最大值.
【解答】
解:如图 2,过点 F 作 FW∥x 轴交直线 OB 于点 W,
设 F(t,t2﹣4t),则 W 的纵坐标为 t2﹣4t,
∵直线 OB 的解析式为 y=x,
∴W(t2﹣4t,t2﹣4t),
∴WF=t﹣(t2﹣4t)=﹣t2+5t,
∵易得 B(5,5),点 E、B 关于抛物线对称轴直线 x=2 对称,
∴BE∥x 轴,BE=6,
∴BE∥WF,
∴△WFG∽△BEG,
∴ = = ,
∵ = = = =﹣ (t﹣ )2+ ,
∴当 t= 时, 的最大值为 .
第 13 页(共 23 页)
例题 2. 已知抛物线 y=﹣x2+2x+3 经过 A、B 两点.P 是抛物线上一点,且在直线 BC 的
上方.连结 AC、AP,AP 交 BC 于点 M,作 PH∥AC 交 BC 于点 H.记△PHM,△PMC,
△CAM 的面积分别为 S1,S2,S3.判断 是否存在最大值.若存在,求出最大值;
若不存在,请说明理由.
【解答】
解法 1 解: 存在最大值,理由如下:
易得 A(﹣1,0),B(3,0)
作 AR∥y 轴交 BC 于 R,过 P 作作 PQ⊥BC 交 BC 于 Q,
由直线 BC 解析式为 y=﹣x+3, A(﹣1,0),
∴R(﹣1,4),
∴AR=4
设 P(t,﹣t2+2t+3),
则 Q(t,﹣t+3),
∴PQ=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t,
∵PH∥AC,易证△PMH∽△AMC,
∴ = = ,
∴ , ,
第 14 页(共 23 页)
∴ ,
∵AR∥PQ,AC∥PH,
可得△ACR∽△PHQ,
PH PQ
∴ = ,
AC AR
S
∴ 1
S 2PH
2 = =﹣ (t﹣ )2+ ,
S2 S3 AC
∴当 t= 时, + 取最大值,最大值为 .
解法 2 解: 存在最大值,理由如下:
易得 A(﹣1,0),B(3,0)
作 AR∥BC 交 y 轴于 R,过 P 作作 PQ⊥BC 交 BC 于 Q,
由直线 BC 解析式为 y=﹣x+3,易得直线 AR 解析式为 y=﹣x﹣1,
令 x=0 得 y=﹣1,∴R(0,﹣1),
∵C(0,3),∴CR=4,
设 P(t,﹣t2+2t+3),则 Q(t,﹣t+3),
∴PQ=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t,
∵PH∥AC,易证△PMH∽△AMC,∴ = = ,
∴ , ,
∴ ,
∵AR∥BC,PH∥AC, PQ∥CR,
可得△ACR∽△HPQ,
PH PQ
∴ = ,
AC CR
S1 S2 2PH∴ = =﹣ (t﹣ )2+ ,
S2 S3 AC
第 15 页(共 23 页)
∴当 t= 时, + 取最大值,最大值为 .
小结:同高三角形面积比等于对应底边的比,可利用平行线把底边比转化为水平线段比
或铅垂线段比。具体到本题,因为 AC 长度是定值,所以表示面积比也可以作 PQ∥y 轴,
直接用含 t 的代数式表示 PQ
(二)跟进练习:
1. 抛物线 y=﹣ ,与 x 轴分别交于 A,B 两点(点 A 在点 B 的左侧),与 y 轴
交于点 C(0,3),抛物线对称轴为 x=1,点 P 是第一象限抛物线上动点,连接 BC,PB.如
图 1,连接 PA,交 BC 于点 M,设△ABM 的面积为 S1,
△PBM 的面积为 S2,求 的最小值及此时点 P 的坐标;
【解答】解:如图,作 PQ∥AB,交 BC 于 Q,
∴△PMQ∽△AMB, ∴ ,
设 P(m,﹣ ),
由﹣ 得,
x= ,
∴PQ=m﹣( )=﹣ +2m,
∵AB=4﹣(﹣2)=6,
第 16 页(共 23 页)
∴ = = ,
∴当 m=2 时,﹣ 的最大值为 2,
∴ 的最小值为 3,
当 m=2 时,y=3, ∴P(2,3);
2. 抛物线 y=﹣ x2+ x+3 与 y 轴交于点 C,与 x 轴交于 A、
B 两点(点 A 在点 B 的左侧),其中 A(﹣ ,0),点 D
为直线 BC 上方抛物线上一点,连接 AD、BC 交于点 E,连
接 BD,记△BDE 的面积为 S1,△ABE 的面积为 S2,求 的
最大值.
【解答】解: 过点 D 作 DG⊥x 轴于点 G,交 BC 于点 F,过点
A 作 AK⊥x 轴交 BC 的延长线于点 K,
∴△DEF∽△AEK,
∴ = ,
∵C(0,3),B(3 ,0),
∴直线 BC 的解析式为:y=﹣ x+3;
设点 D 的横坐标为 t,∴D(t,﹣ t2+ t+3),
∴F(t,﹣ t+3),K(﹣ ,4),
∴AF=4,DF=﹣ t2+ t+3﹣(﹣ t+3)=﹣ t2+ t;
∴ = =﹣ t2+ t=﹣ (t﹣ )2+ ,
第 17 页(共 23 页)
∴当 t= 时, 的最大值为 .
3 2 9
3. 如图,在平面直角坐标系中,抛物线 y x x 3与 x 轴交于点 A(4,0),C(﹣
4 4
1,0)与 y 轴交于点 B, 点 Q 为直线 AB 上方抛物线上一点,
OQ 交 AB 于点 D,QE∥BO 交 AB 于点 E.记△QDE,△QDB,
△BDO 的面积分别为 S1,S2,S3.求 的最大值.
【解答】解:设直线 AB 的解析式为 .
∵4E∥BO,易证△DQE∽△DOB,
∴ ,∴ , ,
∴ .
设 Q 点坐标为 ,则点 E 坐标为 ,
∴ ,
∴当 x=2 时,QE 最大为 3,即 的最大值为 2.
第 18 页(共 23 页)
4. 如图,在平面直角坐标系中,二次函数 y x2 6x 5的图象与 x 轴交于 A、B 两点,
与 y 轴交于点 C,其顶点为 P,连接 PA、 AC 、CP,过点 C 作 y 轴的垂线 l.直线 l上
是否存在点 Q,使△PBQ 的面积等于△PAC 的面积的 2 倍?若存在,求出点 Q 的坐标;
若不存在,请说明理由.
【解答】解:设 PC 与 x 轴交于 E 点,PQ 与坐标轴交于 F 点
1
AE PH
S
∵ MNB 2
AE
S 1 PBQ BFBF PH
2
根据解析式,可得 A(1,0),P(3,4),C(0,-5) B(5,0)
5
∴PC 解析式为: y=3x 5 可得 E( ,0)
3
2
∴AE=
3
4 11 19
∴BF= ∴F( ,0)或 F( ,0)
3 3 3
6 38
∴PF 解析式为: y=-6x 22 或 y=- x
5 5
27 21
当 y=-5 时,可求得 Q( ,-5)或 F( ,-5)
6 2
第 19 页(共 23 页)
5.如图 1,二次函数 y=x2﹣3x﹣4 的图象与 x 轴交于点 A、B 两点,与 y 轴交于点 C,直线
BC 的函数表达式为 y=x﹣4,直线 x=1 与 x 轴交于点 D,P 为直线 x=1 上一动点,连接
PB,将 PB 绕 P 顺时针旋转一定角度得到 PQ.若点 Q 恰好落在抛物线位于第四象限的图
象上,连接 AQ 交 BC 于点 E,连接 AC,CQ,当△CEQ 与△ACE 的面积之比最大时,求点
P 的坐标;
【解答】解: 如图 1,作 AM⊥x 轴交直线 BC 于点 M,作 QN⊥x 轴交直线 BC 于点 N,
则 AM∥QN,
∴△QEN∽△AEM,
∴ = = ,
直线 y=x﹣4,当 x=﹣1 时,y=﹣5,
∴M(﹣1,﹣5),
∴AM=5,
设 Q(m,m2﹣3m﹣4),则 N(m,m﹣4),
∴QN=m﹣4﹣(m2﹣3m﹣4)=﹣m2+4m,
∴ = =﹣ (m﹣2)2+ ,
∴当 m=2 时,△CEQ 与△ACE 的面积之比最大,此时 Q(2,﹣6),
设 P(1,n),
由旋转得 PQ=PB,
∴(1﹣2)2+(n+6)2=(4﹣1)2+(0﹣n)2,
解得 n=﹣ ,∴P(1,﹣ ).
第 20 页(共 23 页)
6.在平面直角坐标系中 xOy 中,二次函数 y=﹣x2+x+2 的图象与 x 轴交于点 A、B,与 y 轴
交于点 C.若点 P 是二次函数图象上位于线段 BC 上方的一个动点.如图,连接 AC,CP,
AP,AP交 BC于点 E,过点 P作AC的平行线交 BC于点Q,将△PEQ与△PCE的面积比
记为 a,将△PCE 与△ACE 的面积比 记为 b,当 a+ b 有最大值时,求点 P 的坐
标;
【解答】解:)①令 x=0,则 y=2,
∴C(0,2),
∴OC=2.
∵A(﹣1,0)、B(2,0),
∴OA=1,OB=2,
∴OB=OC,
∴∠OBC=∠OCB=45°.
过点 P 作 PF⊥x 轴于点 F,交 BC 于点 G,过点 Q 作 QH
⊥PF 于点 H,如图,
设 P(m,﹣m2+m+2),则 OF=m,PF=﹣m2+m+2,
∴BF=OB﹣OF=2﹣m,
∵△GFB 为等腰直角三角形,
∴GF=BF=2﹣m,
∴PG=PF﹣GF=﹣m2+2m.
∵OA=1,OC=2,∴AC= = .
∵AC∥PQ,PF∥OC,
第 21 页(共 23 页)
∴∠ACO=∠FPQ.
∵∠OAC=∠QHP=90°,
∴△OAC∽△HQP,
∴ .
设 QH=n,
∴ ,
∴PH=2n,PQ= n.
∵QH∥OB,
∴∠HQB=∠OBC=45°,
∴△QHG 为等腰直角三角形,
∴GH=QH=n,
∴PG=PH+HG=3n,
∴ ,
∴PQ= (﹣m2+2m).
∵PQ∥AC,∴△PQE∽△ACE,
∴ .
∵等高的三角形的面积比等于底的比,
∴ =a= , =b= ,
∴a=b= = (﹣m2+2m)=﹣ + m.
∴a+ b=(1+ )a=﹣( )(m﹣1)2+ ,
∵﹣( )<0,
∴当 m=1 时,a+ b 有最大值,
∴点 P 的坐标(1,1);
第 22 页(共 23 页)
第 23 页(共 23 页)
同课章节目录
