初中数学人教版八年级下册 18.2.3 正方形教学设计(表格式)
文档属性
| 名称 | 初中数学人教版八年级下册 18.2.3 正方形教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 16:12:44 | ||
图片预览

文档简介
教学设计
课题 正方形
教学内容分析在研究了矩形和菱形的概念、性质与判定的基础上,用直观的方法将矩形和菱形特殊化为正方形,所以正方形既是矩形也是菱形,这为研究正方形性质和判定提供方法.正方形是最特殊的平行四边形,教材从学生已有的经验出发,先得到正方形的部分性质,通过思考”让学生调用己有的研究矩形和菱形的方法研究正方形.因为正方形为本章的末端知识,性质更加丰富,应用更加广泛.本节课的学习将为进一步理解几何对象的性质和判定之间的互逆关系提供依据.
学情分析学生在小学初步接触过正方形的概念,前面刚刚学习了矩形和菱形.知道研究一个几何对象的一般路径:从概念、性质和判定三个视角研究;一般的研究方法:一般到特殊或者从构成图形的几何要素出发研究,这些都是进一步学习正方形的基础.但是,正方形与矩形、菱形之间关系密切又复杂,在从属关系和共同性质方面容易引起混淆,在判定方法的使用上也容易混淆,这是可能存在的问题.
目标确定1.能说出正方形的定义,知道正方形具有矩形和菱形的所有性质.2.能从正方形的定义出发,利用平行四边形的性质定理,推出正方形的性质.3.能用正方形的性质解决问题4.能利用性质与判定的关系,猜想并证明正方形的判定定理。5.能运用正方形的判定定理解决问题.
学习重点难点重点:正方形的概念、性质和判定难点:正方形判定和性质的归纳和应用
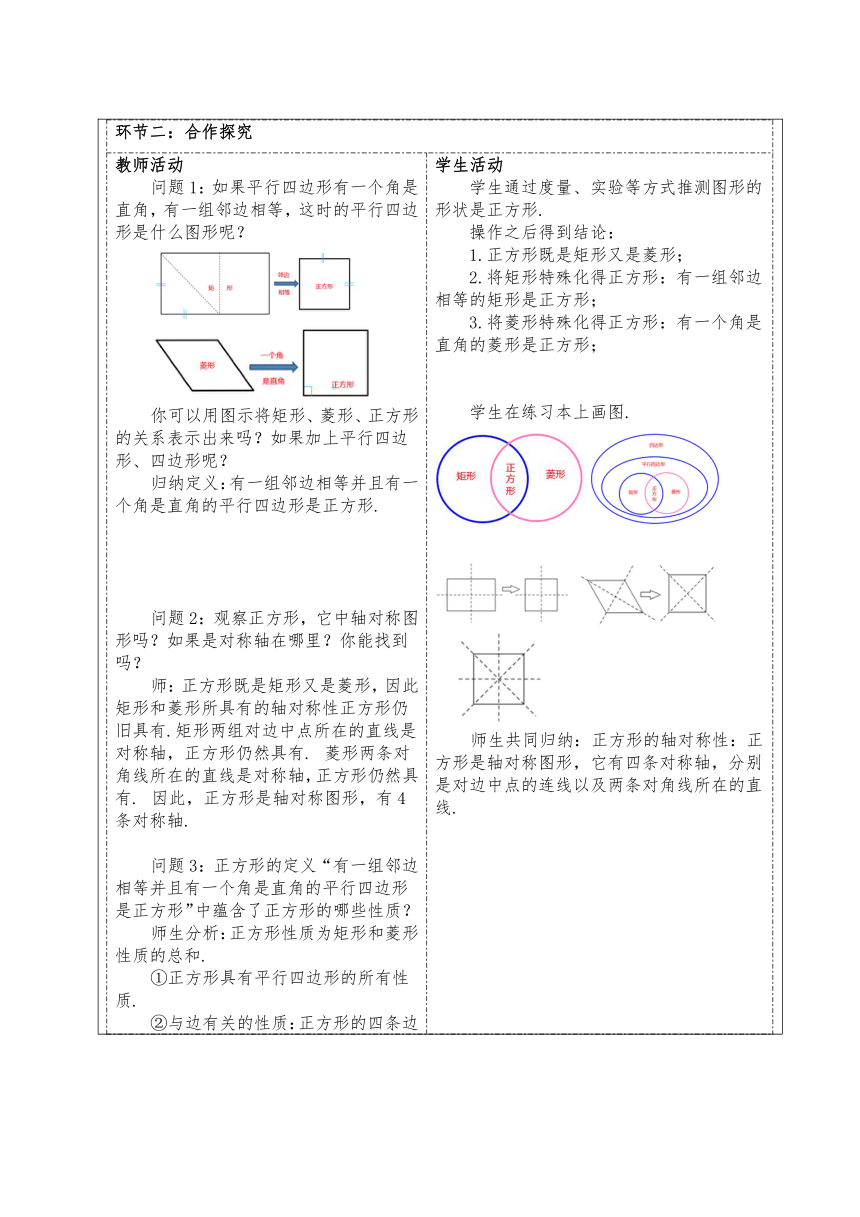
学习活动设计教师活动学生活动环节一:复习导入教师活动除了矩形和菱形外,还有什么特殊的平行四边形呢?怎样研究这类图形?想一想我们是怎样研究矩形和菱形的.通过前两节课的学习已经知道,将平行四边形的边或角特殊化可以得到特殊的平行四边形,回顾这个过程. 学生活动学生回答:正方形有一个角是直角的平行四边形是矩形.有一组邻边相等的平行四边形是菱形.设计意图 通过对已有知识与经验的回顾反思,引导学生提出研究正方形问题。环节二:合作探究教师活动问题1:如果平行四边形有一个角是直角,有一组邻边相等,这时的平行四边形是什么图形呢?你可以用图示将矩形、菱形、正方形的关系表示出来吗?如果加上平行四边形、四边形呢?归纳定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.问题2:观察正方形,它中轴对称图形吗?如果是对称轴在哪里?你能找到吗?师:正方形既是矩形又是菱形,因此矩形和菱形所具有的轴对称性正方形仍旧具有.矩形两组对边中点所在的直线是对称轴,正方形仍然具有. 菱形两条对角线所在的直线是对称轴,正方形仍然具有. 因此,正方形是轴对称图形,有4条对称轴.问题3:正方形的定义“有一组邻边相等并且有一个角是直角的平行四边形是正方形”中蕴含了正方形的哪些性质?师生分析:正方形性质为矩形和菱形性质的总和.①正方形具有平行四边形的所有性质.②与边有关的性质:正方形的四条边都相等.③与角有关的性质:正方形的四个角都是直角.④与对角线有关的性质:对角线互相垂直平分,并且每一条对角线平分一组对角.你能将正方形的性质归纳梳理吗?并用几何语言描述.问题4:由正方形的定义可知:有一组邻边相等并且有一个角是直角的平行四边形是正方形.还有没有其它判定方法呢?通过前面的实验已经发现,将矩形和菱形特殊化可以得到正方形,由此得到正方形的判定定理.判定方法整理:学生活动学生通过度量、实验等方式推测图形的形状是正方形.操作之后得到结论:1.正方形既是矩形又是菱形;2.将矩形特殊化得正方形:有一组邻边相等的矩形是正方形;3.将菱形特殊化得正方形:有一个角是直角的菱形是正方形;学生在练习本上画图.师生共同归纳:正方形的轴对称性:正方形是轴对称图形,它有四条对称轴,分别是对边中点的连线以及两条对角线所在的直线.生归纳梳理:1. 有一组邻边相等的矩形是正方形.2. 对角线互相垂直的矩形是正方形.3. 有一个角是直角的菱形是正方形.4. 对角线相等的菱形是正方形.学生猜想并证明:1.有一组邻边相等的矩形是正方形.2.对角线互相垂直的矩形是正方形.3.有一个角是直角的菱形是正方形.4.对角线相等的菱形是正方形.设计意图问题1:了解正方形的概念,知道正方形既是矩形又是菱形,从集合的视角初步体会一般和特殊之间的关系.问题2:通过正方形对称轴的研究,为了解正方形的几何性质提供了直观的依据.问题3:通过度量、实验操作、几何画板演示等方式,通过合情推理,发现结论,形成猜想,运用演绎推理证明猜想.把合情推理和演绎推理有机结合起来.问题4:从数学本身提出问题,通过正方形性质定理的逆命题,提出问题,通过运用演绎推理证明这些命题的真伪,得出正方形的判定定理,进一步说明正方形的性质定理与判定定理之间的关系.环节三:典例精析教师活动例:求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形. 追问:图中共有多少个等腰直角三角形?学生活动小组合作交流进行推理证明。小组代表上台展示交流成果。教师点评后板书解题过程.证明:∵四边形ABCD是正方形,∴AC=BD,AC⊥BD,OA=0B=OC=OD.∴△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,且△ABO≌△BCO≌△CDO≌△DAO.生答:8个设计意图 利用正方形的性质解决问题,通过此题进一步培养学生的合情推理能力和演绎推理能力.环节四:达标检测教师活动一、选择题1.下列说法错误的是()A.正方形是平行四边形B.正方形是菱形C.正方形是矩形D.菱形和矩形都是正方形2.圆,正方形,长方形,等腰梯形中有唯一条对称轴的是()A.圆B.正方形C.长方形D.等腰梯形3.在口ABCD中,AB=10,BC=14,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为()A.7 B.4或10 C.5或9 D.6或84.如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为 cm.6.如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE= .学生活动 学生独立完成后同伴交流.设计意图 检测学生达标程度.环节五:小结教师活动1.正方形与矩形和菱形有什么关系?2.正方形的性质有哪些?3.怎样证明一个四边形是正方形?学生活动学生畅谈。设计意图 总结归纳,形成知识框图、研究方法路线图。
板书设计正方形例:
教学反思与改进正方形的这种特殊性需要教学时结合图形来具体说明.分清这些平行四边形以及特殊平行四边形的从属关系,从基本研究要素出发,梳理它们的性质定理和判定定理,克服难点.教师需要引导学生从正方形的对称性统领整个课时教学.
学习评价设计达成目标1和2的标志是:知道正方形的四条边相等,四个角相等,有4条对称轴.能画出正方形和矩形,菱形的关系图.知道正方形是菱形(矩形),所以所有菱形(矩形)的性质都适用于正方形,并能分门别类的列举这些性质;达成目标3和5的标志是:会解答教材例题和练习;达成目标4的标志是:能从性质和判定的互逆性,得到正方形的判定;用取交集”的办法得到“既是矩形又是菱形即是正方形”。
4
课题 正方形
教学内容分析在研究了矩形和菱形的概念、性质与判定的基础上,用直观的方法将矩形和菱形特殊化为正方形,所以正方形既是矩形也是菱形,这为研究正方形性质和判定提供方法.正方形是最特殊的平行四边形,教材从学生已有的经验出发,先得到正方形的部分性质,通过思考”让学生调用己有的研究矩形和菱形的方法研究正方形.因为正方形为本章的末端知识,性质更加丰富,应用更加广泛.本节课的学习将为进一步理解几何对象的性质和判定之间的互逆关系提供依据.
学情分析学生在小学初步接触过正方形的概念,前面刚刚学习了矩形和菱形.知道研究一个几何对象的一般路径:从概念、性质和判定三个视角研究;一般的研究方法:一般到特殊或者从构成图形的几何要素出发研究,这些都是进一步学习正方形的基础.但是,正方形与矩形、菱形之间关系密切又复杂,在从属关系和共同性质方面容易引起混淆,在判定方法的使用上也容易混淆,这是可能存在的问题.
目标确定1.能说出正方形的定义,知道正方形具有矩形和菱形的所有性质.2.能从正方形的定义出发,利用平行四边形的性质定理,推出正方形的性质.3.能用正方形的性质解决问题4.能利用性质与判定的关系,猜想并证明正方形的判定定理。5.能运用正方形的判定定理解决问题.
学习重点难点重点:正方形的概念、性质和判定难点:正方形判定和性质的归纳和应用
学习活动设计教师活动学生活动环节一:复习导入教师活动除了矩形和菱形外,还有什么特殊的平行四边形呢?怎样研究这类图形?想一想我们是怎样研究矩形和菱形的.通过前两节课的学习已经知道,将平行四边形的边或角特殊化可以得到特殊的平行四边形,回顾这个过程. 学生活动学生回答:正方形有一个角是直角的平行四边形是矩形.有一组邻边相等的平行四边形是菱形.设计意图 通过对已有知识与经验的回顾反思,引导学生提出研究正方形问题。环节二:合作探究教师活动问题1:如果平行四边形有一个角是直角,有一组邻边相等,这时的平行四边形是什么图形呢?你可以用图示将矩形、菱形、正方形的关系表示出来吗?如果加上平行四边形、四边形呢?归纳定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.问题2:观察正方形,它中轴对称图形吗?如果是对称轴在哪里?你能找到吗?师:正方形既是矩形又是菱形,因此矩形和菱形所具有的轴对称性正方形仍旧具有.矩形两组对边中点所在的直线是对称轴,正方形仍然具有. 菱形两条对角线所在的直线是对称轴,正方形仍然具有. 因此,正方形是轴对称图形,有4条对称轴.问题3:正方形的定义“有一组邻边相等并且有一个角是直角的平行四边形是正方形”中蕴含了正方形的哪些性质?师生分析:正方形性质为矩形和菱形性质的总和.①正方形具有平行四边形的所有性质.②与边有关的性质:正方形的四条边都相等.③与角有关的性质:正方形的四个角都是直角.④与对角线有关的性质:对角线互相垂直平分,并且每一条对角线平分一组对角.你能将正方形的性质归纳梳理吗?并用几何语言描述.问题4:由正方形的定义可知:有一组邻边相等并且有一个角是直角的平行四边形是正方形.还有没有其它判定方法呢?通过前面的实验已经发现,将矩形和菱形特殊化可以得到正方形,由此得到正方形的判定定理.判定方法整理:学生活动学生通过度量、实验等方式推测图形的形状是正方形.操作之后得到结论:1.正方形既是矩形又是菱形;2.将矩形特殊化得正方形:有一组邻边相等的矩形是正方形;3.将菱形特殊化得正方形:有一个角是直角的菱形是正方形;学生在练习本上画图.师生共同归纳:正方形的轴对称性:正方形是轴对称图形,它有四条对称轴,分别是对边中点的连线以及两条对角线所在的直线.生归纳梳理:1. 有一组邻边相等的矩形是正方形.2. 对角线互相垂直的矩形是正方形.3. 有一个角是直角的菱形是正方形.4. 对角线相等的菱形是正方形.学生猜想并证明:1.有一组邻边相等的矩形是正方形.2.对角线互相垂直的矩形是正方形.3.有一个角是直角的菱形是正方形.4.对角线相等的菱形是正方形.设计意图问题1:了解正方形的概念,知道正方形既是矩形又是菱形,从集合的视角初步体会一般和特殊之间的关系.问题2:通过正方形对称轴的研究,为了解正方形的几何性质提供了直观的依据.问题3:通过度量、实验操作、几何画板演示等方式,通过合情推理,发现结论,形成猜想,运用演绎推理证明猜想.把合情推理和演绎推理有机结合起来.问题4:从数学本身提出问题,通过正方形性质定理的逆命题,提出问题,通过运用演绎推理证明这些命题的真伪,得出正方形的判定定理,进一步说明正方形的性质定理与判定定理之间的关系.环节三:典例精析教师活动例:求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形. 追问:图中共有多少个等腰直角三角形?学生活动小组合作交流进行推理证明。小组代表上台展示交流成果。教师点评后板书解题过程.证明:∵四边形ABCD是正方形,∴AC=BD,AC⊥BD,OA=0B=OC=OD.∴△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,且△ABO≌△BCO≌△CDO≌△DAO.生答:8个设计意图 利用正方形的性质解决问题,通过此题进一步培养学生的合情推理能力和演绎推理能力.环节四:达标检测教师活动一、选择题1.下列说法错误的是()A.正方形是平行四边形B.正方形是菱形C.正方形是矩形D.菱形和矩形都是正方形2.圆,正方形,长方形,等腰梯形中有唯一条对称轴的是()A.圆B.正方形C.长方形D.等腰梯形3.在口ABCD中,AB=10,BC=14,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为()A.7 B.4或10 C.5或9 D.6或84.如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为 cm.6.如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE= .学生活动 学生独立完成后同伴交流.设计意图 检测学生达标程度.环节五:小结教师活动1.正方形与矩形和菱形有什么关系?2.正方形的性质有哪些?3.怎样证明一个四边形是正方形?学生活动学生畅谈。设计意图 总结归纳,形成知识框图、研究方法路线图。
板书设计正方形例:
教学反思与改进正方形的这种特殊性需要教学时结合图形来具体说明.分清这些平行四边形以及特殊平行四边形的从属关系,从基本研究要素出发,梳理它们的性质定理和判定定理,克服难点.教师需要引导学生从正方形的对称性统领整个课时教学.
学习评价设计达成目标1和2的标志是:知道正方形的四条边相等,四个角相等,有4条对称轴.能画出正方形和矩形,菱形的关系图.知道正方形是菱形(矩形),所以所有菱形(矩形)的性质都适用于正方形,并能分门别类的列举这些性质;达成目标3和5的标志是:会解答教材例题和练习;达成目标4的标志是:能从性质和判定的互逆性,得到正方形的判定;用取交集”的办法得到“既是矩形又是菱形即是正方形”。
4
