重庆市南坪中学校2024-2025学年高二上学期期中考试数学试卷(含答案)
文档属性
| 名称 | 重庆市南坪中学校2024-2025学年高二上学期期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 852.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 17:23:01 | ||
图片预览



文档简介
重庆市南坪中学校2024-2025学年高二上学期期中考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知向量,,则( )
A. B.0 C.1 D.2
2.经过,两点的直线的倾斜角是( )
A. B. C. D.
3.已知圆C的方程是,则圆心C的坐标是( )
A. B. C. D.
4.抛物线的焦点到其准线的距离为( )
A. B.1 C.2 D.4
5.我国古代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”,意思是说,有一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切),如图所示已知圆O的半径为2丈,过C作圆O的两条切线,切点分别为M,N,若,则对角线AC长度为( )
A.丈 B.丈
C.丈 D.丈
6.设椭圆的两个焦点分别为,,过作椭圆长轴的垂线交椭圆于点P,若为等腰直角三角形,则椭圆的离心率是( )
A. B. C. D.
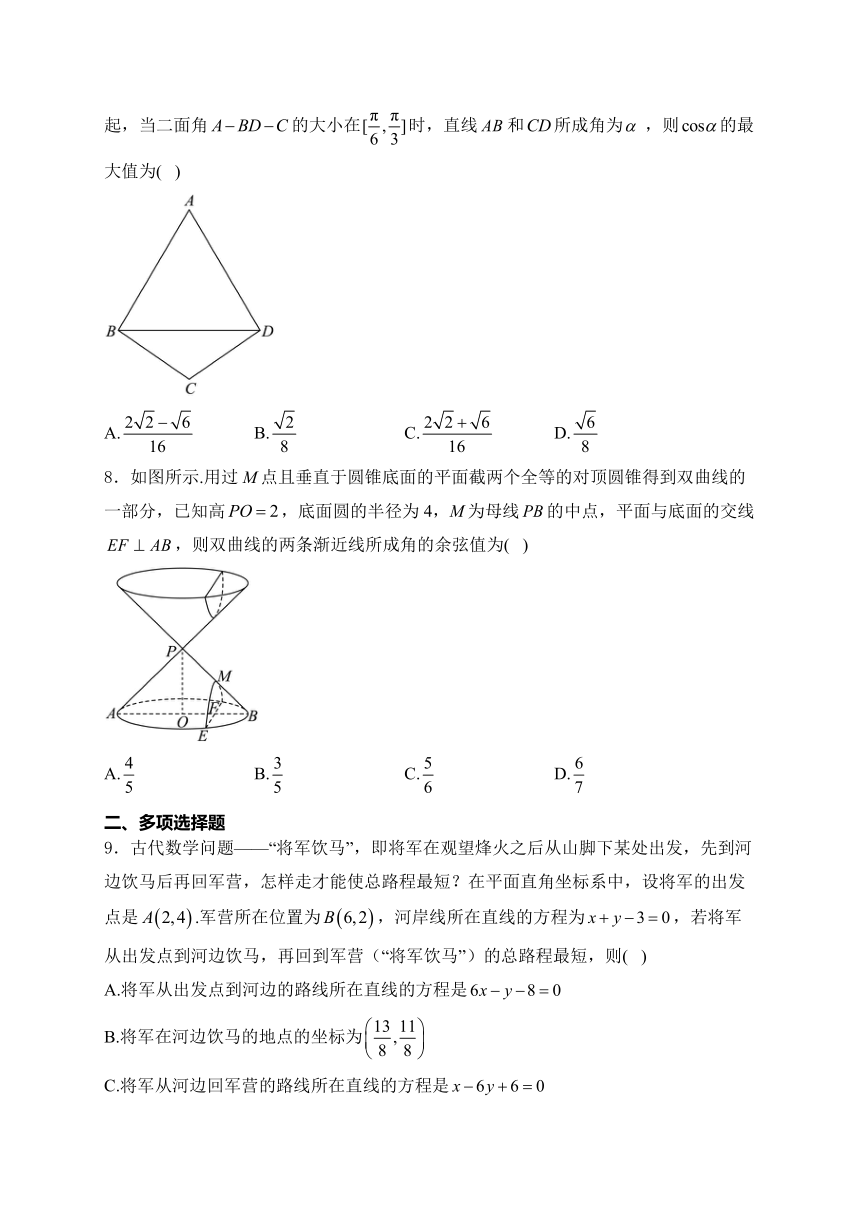
7.如图,四边形,,现将沿折起,当二面角的大小在时,直线和所成角为,则的最大值为( )
A. B. C. D.
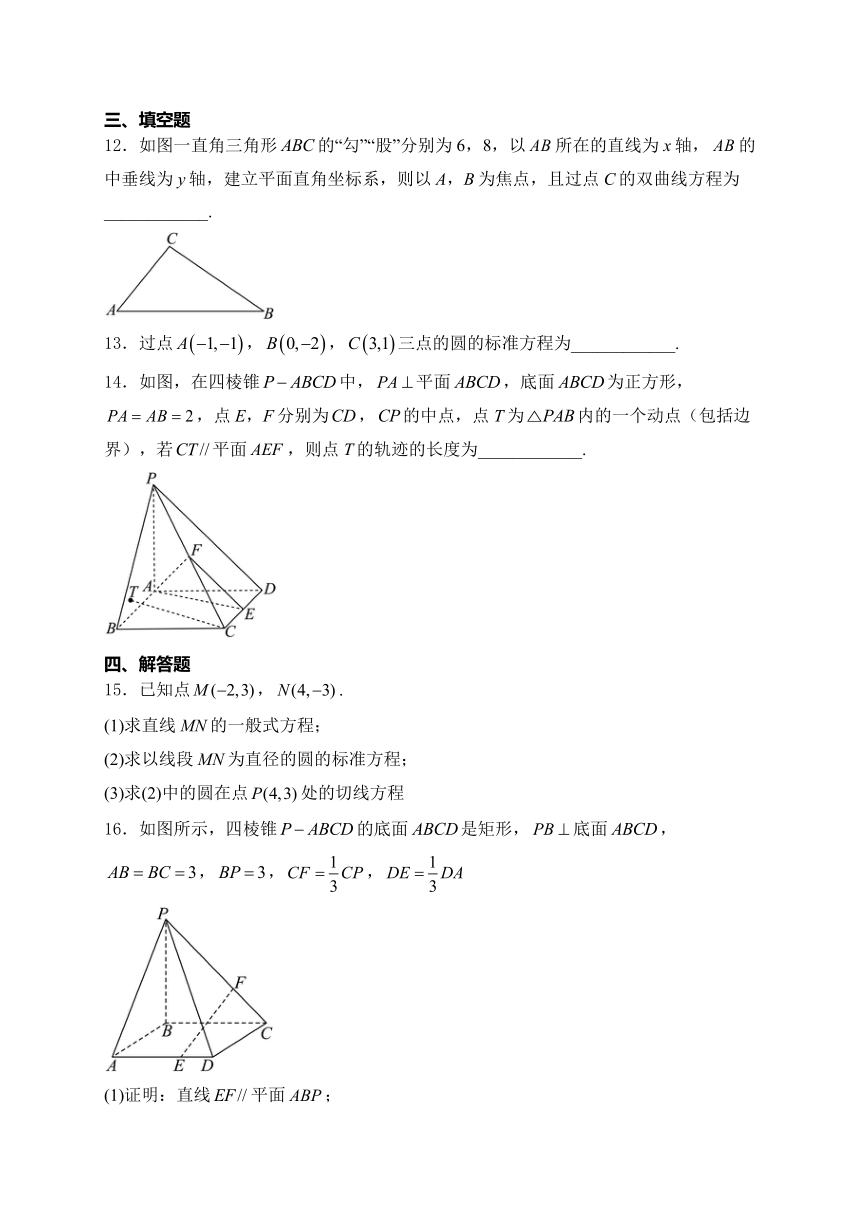
8.如图所示.用过M点且垂直于圆锥底面的平面截两个全等的对顶圆锥得到双曲线的一部分,已知高,底面圆的半径为4,M为母线的中点,平面与底面的交线,则双曲线的两条渐近线所成角的余弦值为( )
A. B. C. D.
二、多项选择题
9.古代数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设将军的出发点是.军营所在位置为,河岸线所在直线的方程为,若将军从出发点到河边饮马,再回到军营(“将军饮马”)的总路程最短,则( )
A.将军从出发点到河边的路线所在直线的方程是
B.将军在河边饮马的地点的坐标为
C.将军从河边回军营的路线所在直线的方程是
D.“将军饮马”走过的总路程为
10.如图,已知正方体的棱长为a,则下列选项中正确的有( )
A.异面直线与的夹角的正弦值为
B.二面角的平面角的正切值为
C.四棱锥的外接球体积为
D.三棱锥与三棱锥体积相等
11.如图是数学家GerminalDandelin用来证明一个平面截圆锥侧面得到的截口曲线是椭圆的模型(称为“Dandelin双球”)在圆锥内放两个大小不同的小球,使得它们分别与圆锥的侧面、截面相切,截面分别与球,球切于点E,F(E,F是截口椭圆C的焦点)设图中球,球的半径分别为4和1,球心距,则( )
A.椭圆C的中心不在直线上
B.
C.直线与椭圆C所在平面所成的角的正弦值为
D.椭圆C的离心率为
三、填空题
12.如图一直角三角形的“勾”“股”分别为6,8,以所在的直线为x轴,的中垂线为y轴,建立平面直角坐标系,则以A,B为焦点,且过点C的双曲线方程为____________.
13.过点,,三点的圆的标准方程为____________.
14.如图,在四棱锥中,平面,底面为正方形,,点E,F分别为,的中点,点T为内的一个动点(包括边界),若平面,则点T的轨迹的长度为____________.
四、解答题
15.已知点,.
(1)求直线MN的一般式方程;
(2)求以线段MN为直径的圆的标准方程;
(3)求(2)中的圆在点处的切线方程
16.如图所示,四棱锥的底面是矩形,底面,,,,
(1)证明:直线平面;
(2)求点P到平面的距离
17.设向量,满足.
(1)求动点的轨迹C的方程;
(2)若点,,设斜率为且过的直线l与(1)中的轨迹交于P,Q两点,求的面积
18.如图所示的几何体中,PD垂直于梯形ABCD所在的平面,,F为PA的中点,,,四边形PDCE为矩形,线段PC交DE于点N.
(1)求证:平面DEF;
(2)求二面角的余弦值;
(3)在线段EF上是否存在一点Q,使得BQ与平面BCP所成角的大小为?若存在,求出FQ的长;若不存在,请说明理由
19.如图,已知椭圆的上顶点为,离心率为,若过点A作圆的两条切线分别与椭圆C相交于点B,D(不同于点A).
(1)求椭圆C的方程;
(2)设直线和的斜率分别为,,求证:为定值;
(3)求证:直线过定点
参考答案
1.答案:B
2.答案:C
3.答案:A
4.答案:C
5.答案:A
6.答案:C
7.答案:B
8.答案:B
9.答案:BD
10.答案:ACD
11.答案:ACD
12.答案:
13.答案:
14.答案:
15.(1)直线MN的斜率为,
则直线MN的方程为,
即.
(2)由题意可知圆心C为线段MN的中点,即,
半径,
故所求圆的标准方程为.
(3)直线CP的斜率为,
则所求切线的斜率为-1,
故所求的切线方程为,
即.
16.(1)由平面,
且四边形为矩形,可建立如图所示空间直角坐标系,
则,,,,
由,得,
解得,同理,
,
显然面的一个法向量为,
显然且面,
故面
(2)设面的一个法向量为,
且,
由,
取,则,
所以为平面的一个法向量,
又,
点P到平面的距离为.
17.(1)由
得,
由椭圆定义知:点到两定点,的距离之和为4,
且,
所以,,,所以可得
所以点的轨迹C的方程为:.
(2)因为,
所以直线l方程为,
联立方程组
得,
设,
则,
所以
点到直线PQ的距离
所以
18.(1)因为四边形PDCE为矩形,
所以N为PC的中点,连接FN,
在中,F、N分别为PA、PC的中点,
所以,
因为平面DEF,平面DEF,
所以平面DEF;
(2)因为PD垂直于梯形ABCD所在的平面,
又AD、DC在平面ABCD内,
所以,
又,所以,
如图以D为原点,分别以DA、DC、DP所在直线为x、y、z轴,
建立空间直角坐标系,
则,,,
所以,
,
设平面PBC的法向量为,
则,即,
解得,
令,则,
所以平面PBC的一个法向量为,
设平面ABP的法向量为,
,
令,则,
所以平面ABP的一个法向量为,
,
因为二面角的平面角是钝角,
所以二面角的平面角余弦值为,
(3)设存在点Q满足条件,
由,
设,
则
,
因为BQ与平面BCP所成角的大小为,
所以
,
解得,又,
所以,即Q点E与重合,
故在线段EF上存在一点Q,
且.
19.(1)因为椭圆的上顶点为,
离心率为
则
解得,,
所以椭圆C的方程为.
(2)圆M的圆心为,半径为r,
设切线方程为,则,
即
因为两切线,的斜率分别为,
则,是上述方程的两根,根据韦达定理可得:为定值
(3)联立方程,
消掉y得,
设,
则,
同理可得,
则,
可得直线方程为,
令,得,
所以故直线过定点.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知向量,,则( )
A. B.0 C.1 D.2
2.经过,两点的直线的倾斜角是( )
A. B. C. D.
3.已知圆C的方程是,则圆心C的坐标是( )
A. B. C. D.
4.抛物线的焦点到其准线的距离为( )
A. B.1 C.2 D.4
5.我国古代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”,意思是说,有一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切),如图所示已知圆O的半径为2丈,过C作圆O的两条切线,切点分别为M,N,若,则对角线AC长度为( )
A.丈 B.丈
C.丈 D.丈
6.设椭圆的两个焦点分别为,,过作椭圆长轴的垂线交椭圆于点P,若为等腰直角三角形,则椭圆的离心率是( )
A. B. C. D.
7.如图,四边形,,现将沿折起,当二面角的大小在时,直线和所成角为,则的最大值为( )
A. B. C. D.
8.如图所示.用过M点且垂直于圆锥底面的平面截两个全等的对顶圆锥得到双曲线的一部分,已知高,底面圆的半径为4,M为母线的中点,平面与底面的交线,则双曲线的两条渐近线所成角的余弦值为( )
A. B. C. D.
二、多项选择题
9.古代数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设将军的出发点是.军营所在位置为,河岸线所在直线的方程为,若将军从出发点到河边饮马,再回到军营(“将军饮马”)的总路程最短,则( )
A.将军从出发点到河边的路线所在直线的方程是
B.将军在河边饮马的地点的坐标为
C.将军从河边回军营的路线所在直线的方程是
D.“将军饮马”走过的总路程为
10.如图,已知正方体的棱长为a,则下列选项中正确的有( )
A.异面直线与的夹角的正弦值为
B.二面角的平面角的正切值为
C.四棱锥的外接球体积为
D.三棱锥与三棱锥体积相等
11.如图是数学家GerminalDandelin用来证明一个平面截圆锥侧面得到的截口曲线是椭圆的模型(称为“Dandelin双球”)在圆锥内放两个大小不同的小球,使得它们分别与圆锥的侧面、截面相切,截面分别与球,球切于点E,F(E,F是截口椭圆C的焦点)设图中球,球的半径分别为4和1,球心距,则( )
A.椭圆C的中心不在直线上
B.
C.直线与椭圆C所在平面所成的角的正弦值为
D.椭圆C的离心率为
三、填空题
12.如图一直角三角形的“勾”“股”分别为6,8,以所在的直线为x轴,的中垂线为y轴,建立平面直角坐标系,则以A,B为焦点,且过点C的双曲线方程为____________.
13.过点,,三点的圆的标准方程为____________.
14.如图,在四棱锥中,平面,底面为正方形,,点E,F分别为,的中点,点T为内的一个动点(包括边界),若平面,则点T的轨迹的长度为____________.
四、解答题
15.已知点,.
(1)求直线MN的一般式方程;
(2)求以线段MN为直径的圆的标准方程;
(3)求(2)中的圆在点处的切线方程
16.如图所示,四棱锥的底面是矩形,底面,,,,
(1)证明:直线平面;
(2)求点P到平面的距离
17.设向量,满足.
(1)求动点的轨迹C的方程;
(2)若点,,设斜率为且过的直线l与(1)中的轨迹交于P,Q两点,求的面积
18.如图所示的几何体中,PD垂直于梯形ABCD所在的平面,,F为PA的中点,,,四边形PDCE为矩形,线段PC交DE于点N.
(1)求证:平面DEF;
(2)求二面角的余弦值;
(3)在线段EF上是否存在一点Q,使得BQ与平面BCP所成角的大小为?若存在,求出FQ的长;若不存在,请说明理由
19.如图,已知椭圆的上顶点为,离心率为,若过点A作圆的两条切线分别与椭圆C相交于点B,D(不同于点A).
(1)求椭圆C的方程;
(2)设直线和的斜率分别为,,求证:为定值;
(3)求证:直线过定点
参考答案
1.答案:B
2.答案:C
3.答案:A
4.答案:C
5.答案:A
6.答案:C
7.答案:B
8.答案:B
9.答案:BD
10.答案:ACD
11.答案:ACD
12.答案:
13.答案:
14.答案:
15.(1)直线MN的斜率为,
则直线MN的方程为,
即.
(2)由题意可知圆心C为线段MN的中点,即,
半径,
故所求圆的标准方程为.
(3)直线CP的斜率为,
则所求切线的斜率为-1,
故所求的切线方程为,
即.
16.(1)由平面,
且四边形为矩形,可建立如图所示空间直角坐标系,
则,,,,
由,得,
解得,同理,
,
显然面的一个法向量为,
显然且面,
故面
(2)设面的一个法向量为,
且,
由,
取,则,
所以为平面的一个法向量,
又,
点P到平面的距离为.
17.(1)由
得,
由椭圆定义知:点到两定点,的距离之和为4,
且,
所以,,,所以可得
所以点的轨迹C的方程为:.
(2)因为,
所以直线l方程为,
联立方程组
得,
设,
则,
所以
点到直线PQ的距离
所以
18.(1)因为四边形PDCE为矩形,
所以N为PC的中点,连接FN,
在中,F、N分别为PA、PC的中点,
所以,
因为平面DEF,平面DEF,
所以平面DEF;
(2)因为PD垂直于梯形ABCD所在的平面,
又AD、DC在平面ABCD内,
所以,
又,所以,
如图以D为原点,分别以DA、DC、DP所在直线为x、y、z轴,
建立空间直角坐标系,
则,,,
所以,
,
设平面PBC的法向量为,
则,即,
解得,
令,则,
所以平面PBC的一个法向量为,
设平面ABP的法向量为,
,
令,则,
所以平面ABP的一个法向量为,
,
因为二面角的平面角是钝角,
所以二面角的平面角余弦值为,
(3)设存在点Q满足条件,
由,
设,
则
,
因为BQ与平面BCP所成角的大小为,
所以
,
解得,又,
所以,即Q点E与重合,
故在线段EF上存在一点Q,
且.
19.(1)因为椭圆的上顶点为,
离心率为
则
解得,,
所以椭圆C的方程为.
(2)圆M的圆心为,半径为r,
设切线方程为,则,
即
因为两切线,的斜率分别为,
则,是上述方程的两根,根据韦达定理可得:为定值
(3)联立方程,
消掉y得,
设,
则,
同理可得,
则,
可得直线方程为,
令,得,
所以故直线过定点.
同课章节目录
