初中数学人教版九年级下册 27.2.2 相似三角形的性质 导学案(无答案)
文档属性
| 名称 | 初中数学人教版九年级下册 27.2.2 相似三角形的性质 导学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 578.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 18:09:29 | ||
图片预览

文档简介
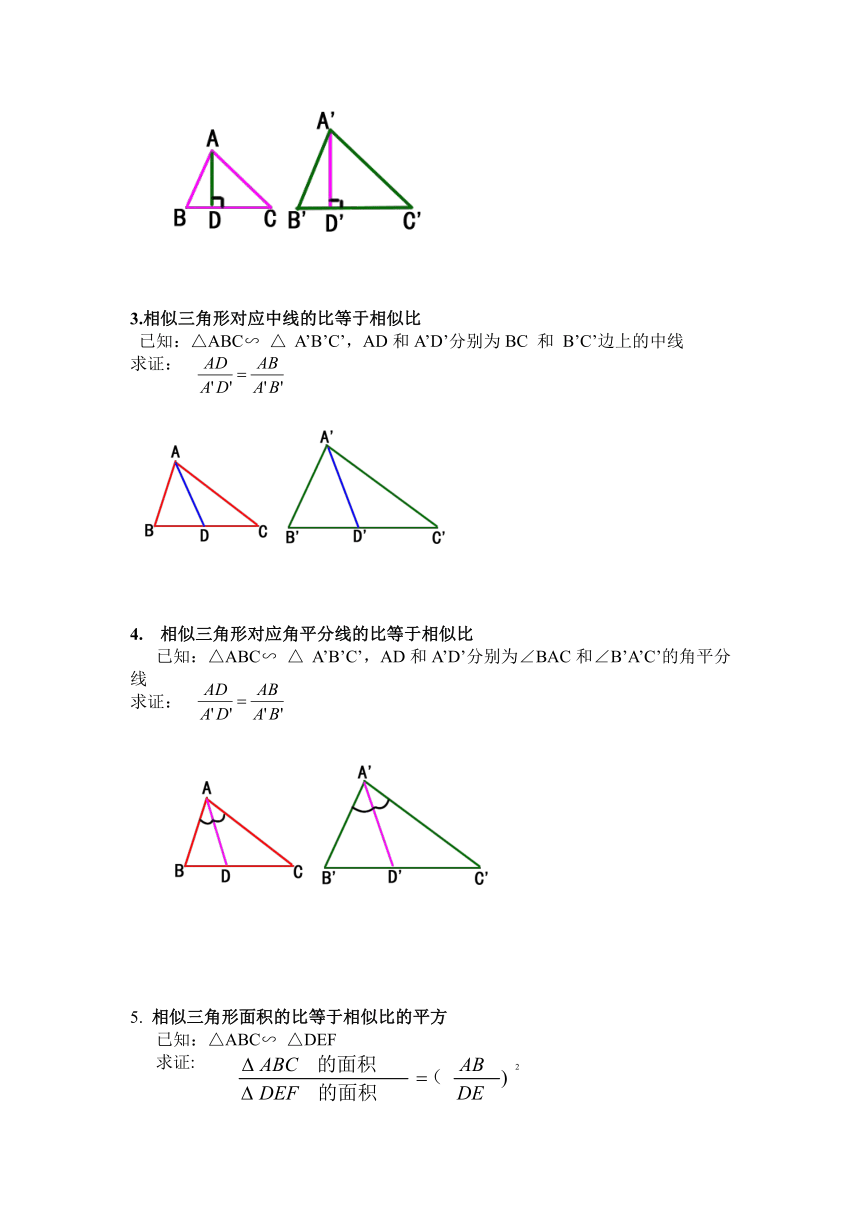
《相似三角形的周长和面积》导学案
学习目标
1. 理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方.
2. 能用三角形的特有性质解决简单的问题.
重点、难点
1.重点:相似三角形的性质与运用.
2.难点:相似三角形性质的灵活运用,及对“相似三角形面积的比等于相似比的平方”性质的理解,特别是对它的反向应用的理解,即对“由面积比求相似比”的理解.
一、自主学习
相似三角形周长的比、对应高的比、对应中线的比、对应角平分线的比、面积的比与相似比的关系。
二、合作交流
1. 相似三角形周长的比等于相似比
已知:△ABC∽△DEF
求证:
2. 相似三角形对应高的比等于相似比
已知:△ABC∽△ A’B’C’ , AD、A’D’分别是BC和B’C’边上的高.
求证:
3.相似三角形对应中线的比等于相似比
已知:△ABC∽ △ A’B’C’,AD和A’D’分别为BC 和 B’C’边上的中线
求证:
4. 相似三角形对应角平分线的比等于相似比
已知:△ABC∽ △ A’B’C’,AD和A’D’分别为∠BAC和∠B’A’C’的角平分线
求证:
5. 相似三角形面积的比等于相似比的平方
已知:△ABC∽ △DEF
求证:
6.通过以上学习,我发现
三、质疑探究
第一关 明辨是非
1 判断:
(1)一个三角形的各边长扩大为原来的5倍.这个三角形的周长
也扩大为原来的5倍; ( )
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍. ( )
第二关 慧眼识珠
2.两个相似三角形面积的比为4:9,则它们对应高的比为( )
A 3:2 B 2:3 C 9:4 D 4:9
3.已知D.E分别为△ABC的AB.AC边上的一点,DE∥BC,且△ADE与四边形DBCE的
面积之比为1:3,则AD:AB的值为( )
A 1:4 B 1:3 C1:2 D2:3
4.一个五边形各边的长分别为1,2,3,4,5,另一个和它相似的五边形的最大边的长为7,则后一个五边形的周长为( )
A 27 B 25 C21 D18
第三关 速度比拼
5 、两个相似多边形的相似比为3:4,它们的面积之差为14,则较大多边形的面积为 _____
6、D、F是AB的三等分点,且DE∥FG ∥ BC,则图中三部分图形的面积之比S1:S2:S3=_____
第四关 自主尝试
7.如图,这是圆桌正上方的灯泡A(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)阴影的示意图. 已知桌面直径DE为1.2米,桌面离地面1米. 若灯泡离地面3米,求地面上阴影部分的面积
四、测评反馈
1. 如果两个相似三角形对应边的比为3∶5 ,那么它们的相似比为________,周长的比为_____,面积的比为_____.
2.如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= .
3.若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则
DE= cm
E
D
C
B
A
S3
S2
S1
学习目标
1. 理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方.
2. 能用三角形的特有性质解决简单的问题.
重点、难点
1.重点:相似三角形的性质与运用.
2.难点:相似三角形性质的灵活运用,及对“相似三角形面积的比等于相似比的平方”性质的理解,特别是对它的反向应用的理解,即对“由面积比求相似比”的理解.
一、自主学习
相似三角形周长的比、对应高的比、对应中线的比、对应角平分线的比、面积的比与相似比的关系。
二、合作交流
1. 相似三角形周长的比等于相似比
已知:△ABC∽△DEF
求证:
2. 相似三角形对应高的比等于相似比
已知:△ABC∽△ A’B’C’ , AD、A’D’分别是BC和B’C’边上的高.
求证:
3.相似三角形对应中线的比等于相似比
已知:△ABC∽ △ A’B’C’,AD和A’D’分别为BC 和 B’C’边上的中线
求证:
4. 相似三角形对应角平分线的比等于相似比
已知:△ABC∽ △ A’B’C’,AD和A’D’分别为∠BAC和∠B’A’C’的角平分线
求证:
5. 相似三角形面积的比等于相似比的平方
已知:△ABC∽ △DEF
求证:
6.通过以上学习,我发现
三、质疑探究
第一关 明辨是非
1 判断:
(1)一个三角形的各边长扩大为原来的5倍.这个三角形的周长
也扩大为原来的5倍; ( )
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍. ( )
第二关 慧眼识珠
2.两个相似三角形面积的比为4:9,则它们对应高的比为( )
A 3:2 B 2:3 C 9:4 D 4:9
3.已知D.E分别为△ABC的AB.AC边上的一点,DE∥BC,且△ADE与四边形DBCE的
面积之比为1:3,则AD:AB的值为( )
A 1:4 B 1:3 C1:2 D2:3
4.一个五边形各边的长分别为1,2,3,4,5,另一个和它相似的五边形的最大边的长为7,则后一个五边形的周长为( )
A 27 B 25 C21 D18
第三关 速度比拼
5 、两个相似多边形的相似比为3:4,它们的面积之差为14,则较大多边形的面积为 _____
6、D、F是AB的三等分点,且DE∥FG ∥ BC,则图中三部分图形的面积之比S1:S2:S3=_____
第四关 自主尝试
7.如图,这是圆桌正上方的灯泡A(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)阴影的示意图. 已知桌面直径DE为1.2米,桌面离地面1米. 若灯泡离地面3米,求地面上阴影部分的面积
四、测评反馈
1. 如果两个相似三角形对应边的比为3∶5 ,那么它们的相似比为________,周长的比为_____,面积的比为_____.
2.如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= .
3.若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则
DE= cm
E
D
C
B
A
S3
S2
S1
