第三章 圆 小结与复习课件(51张PPT)2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 第三章 圆 小结与复习课件(51张PPT)2024-2025学年北师大版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 19:04:45 | ||
图片预览





文档简介
(共51张PPT)
小结与复习
第三章 圆
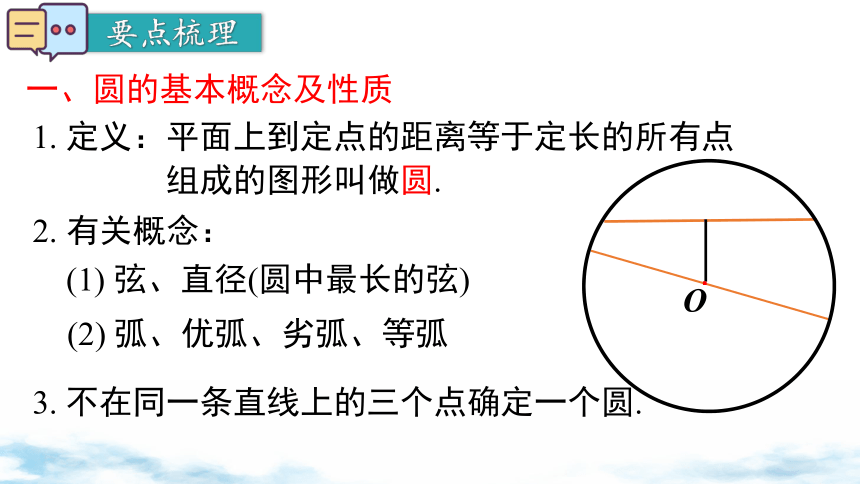
一、圆的基本概念及性质
1. 定义:平面上到定点的距离等于定长的所有点
组成的图形叫做圆.
2. 有关概念:
(1) 弦、直径(圆中最长的弦)
(2) 弧、优弧、劣弧、等弧
.
O
3. 不在同一条直线上的三个点确定一个圆.
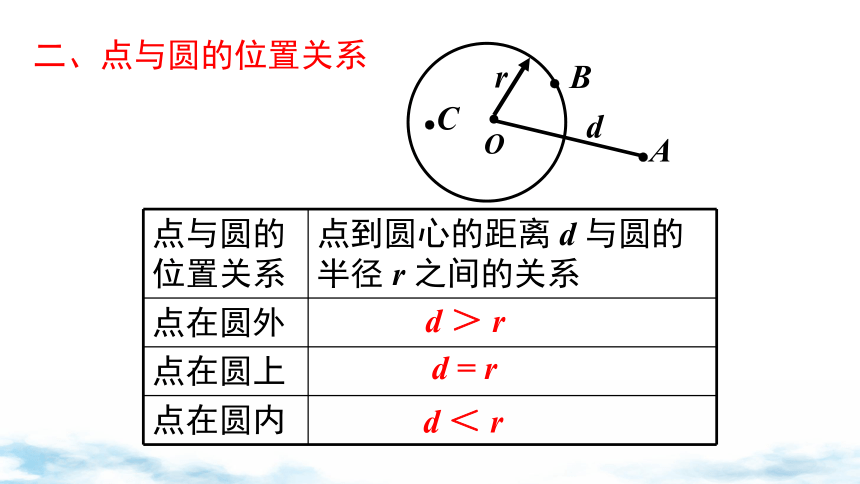
二、点与圆的位置关系
●A
● B
●C
点与圆的位置关系 点到圆心的距离 d 与圆的半径 r 之间的关系
点在圆外
点在圆上
点在圆内
●O
d
r
d > r
d = r
d < r
三、圆的对称性
1. 圆是轴对称图形,经过圆心的每一条直线都是
它的对称轴.圆有无数条对称轴.
2. 圆是中心对称图形,并且绕圆心旋转任何一
个角度都能与自身重合,
即圆具有旋转不变性.
.
3.在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、
两条弦中有一组量相等,那么它们所对应的其余
各组量都分别相等.
●O
A
B
C
D
M└
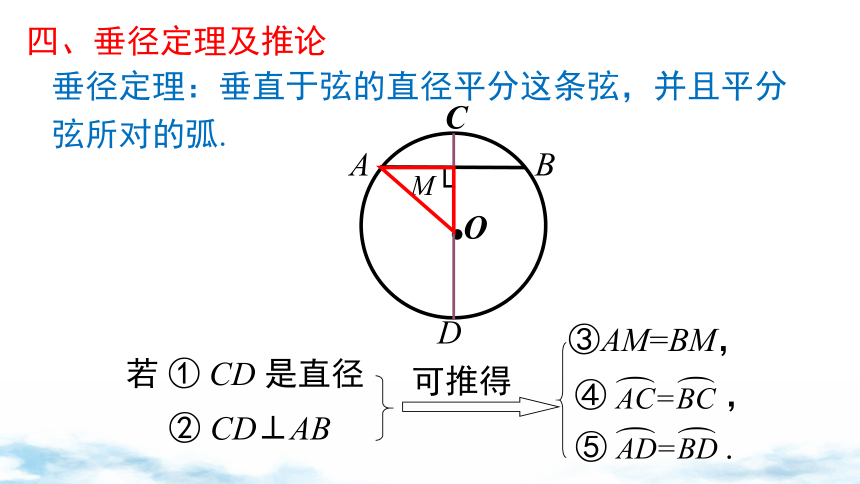
③AM=BM,
若 ① CD 是直径
② CD⊥AB
可推得
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
四、垂径定理及推论
④ ,
⑤ .
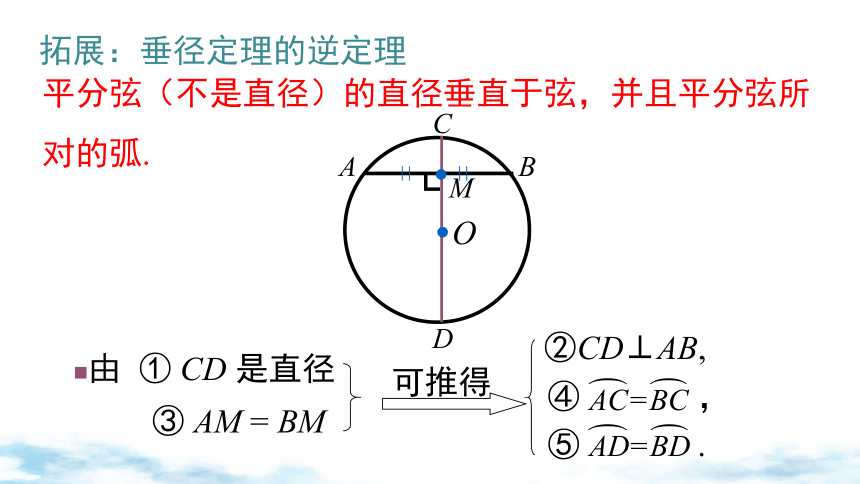
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
拓展:垂径定理的逆定理
②CD⊥AB,
由 ① CD 是直径
③ AM = BM
可推得
O
C
D
A
B
●
┗
M
④ ,
⑤ .
●
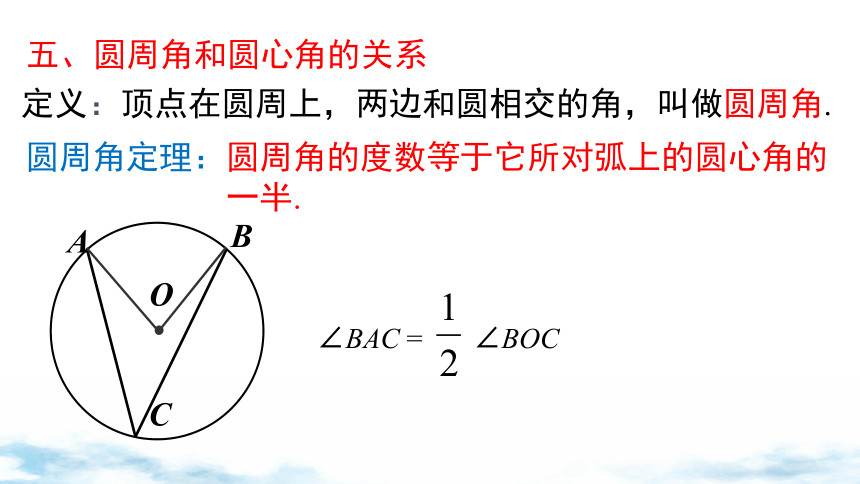
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角的
一半.
五、圆周角和圆心角的关系
∠BAC = ∠BOC
C
A
B
O
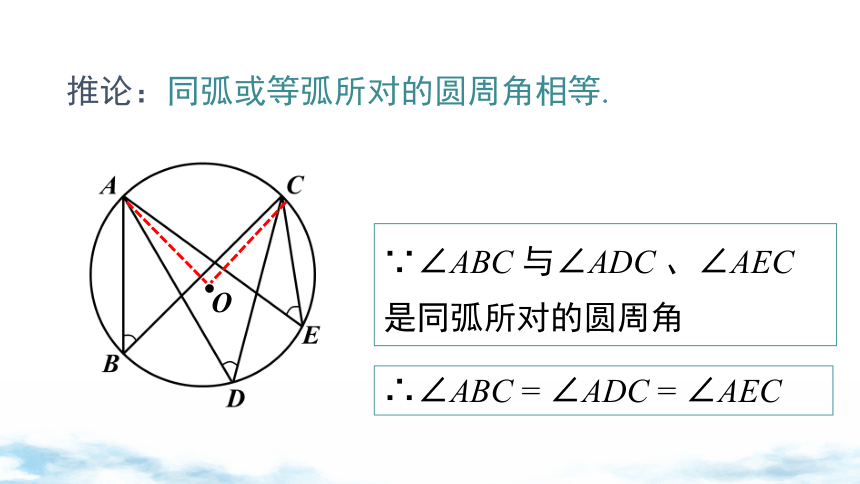
推论:同弧或等弧所对的圆周角相等.
∵∠ABC 与∠ADC 、∠AEC 是同弧所对的圆周角
∴∠ABC = ∠ADC = ∠AEC
●
O
推论:直径所对的圆周角是直角;
90° 的圆周角所对的弦是圆的直径.
推论:圆的内接四边形的对角互补.
A
B
O
C
D
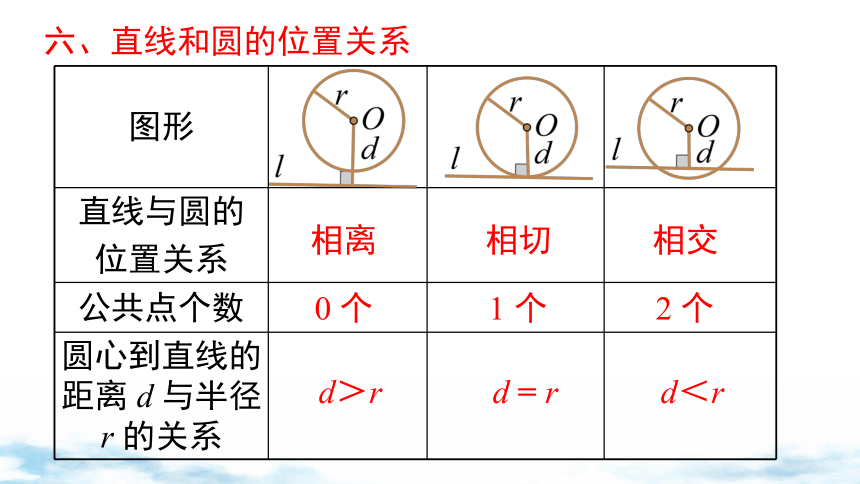
六、直线和圆的位置关系
图形
直线与圆的 位置关系
公共点个数
圆心到直线的距离 d 与半径 r 的关系
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
七、切线的判定与性质
1. 切线的判定一般有三种方法:
a. 定义法:和圆有唯一的一个公共点
b. 距离法: d = r
c. 判定定理:过半径的外端且垂直于半径
2. 切线的性质
圆的切线垂直于过切点的半径.
切线长定理:
过圆外一点画圆的两条切线,它们的切线长相等.
拓展:这一点和圆心的连线平分这两条切线的夹角.
切线长:
过圆外一点画圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
3.切线长及切线长定理
八、三角形的内切圆及内心
1. 与三角形各边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做三角形的内心.
3. 三角形的内心就是三角形的三条角平分线的交点.
三角形的内心到三角形的三边的距离相等.
O
C
D
A
B
M
半径 R
圆心角
弦心距 d
弦a
圆心
中心角
A
B
C
D
E
F
O
半径 R
边心距 r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
M
九、圆内接正多边形
1.正 n 边形的中心角=
C
D
O
B
E
F
A
P
3. 正 n 边形的边长 a,半径 R,边心距 r 之间的关系:
a
R
r
4. 边长 a,边心距 r 的正 n 边形面积的计算:
其中 l 为正 n 边形的周长.
2.正多边形的内角=
计算公式:
(1) 弧长公式:
(2) 扇形面积公式:
十、弧长及扇形的面积
例1 如图,在 ⊙O 中,∠ABC = 50°,则 ∠CAO
等于( )
A.30° B.40°
C.50° D.60°
B
考点一 圆的有关概念及性质
例2 在图中,BC 是 ☉O 的直径,AD⊥BC,若∠D=36°,则 ∠BAD 的度数是( )
A. 72° B. 54°
C. 45° D. 36 °
A
B
C
D
B
例3 ☉O 的半径为 r,圆心到点 A 的距离为 d,且 r、d 分别是方程 x2-6x+8=0 的两根,则点 A 与 ☉O 的位置关系是( )
A.点 A 在 ☉O 内部 B.点 A 在 ☉O 上
C.点 A 在 ☉O 外部 D.点 A 不在 ☉O 上
解析:此题需先计算出一元二次方程 x2-6x+8=0 的两个根,然后再根据R与d的之间的关系判断出点 A 与 ☉O 的关系.
D
1. 如图所示,在圆 O 中弦 AB∥CD,若 ∠ABC=50°,则 ∠BOD 等于( )
A.50° B.40° C.100° D.80°
C
针对训练
2.如图所示,四边形 ABCD 为 ☉O 的内接正方形,点 P 为劣弧 BC 上的任意一点(不与 B,C 重合),则∠BPC 的度数是 .
135°
C
D
B
A
P
O
考点二 垂径定理
例4 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是 10 mm,测得钢珠顶端离零件表面的距离为 8 mm,如图所示,则这个小圆孔的宽口 AB 的长度
为 mm.
8mm
A
B
8
C
D
O
解析:设圆心为 O,连接 AO,作出过点 O 的弓形高 CD,垂足为 D,可知AO=5 mm,OD=3 mm,利用勾股定理进行计算,AD=4 mm,所以 AB=8 mm.
3. 如图 a,点 C 是扇形 OAB 上的 的任意一点,OA=2,连接 AC,BC,过点 O 作 OE ⊥AC,OF ⊥BC,垂足分别为E,F,连接 EF,则 EF 的长度等于 .
A
O
B
C
E
F
图 a
针对训练
4. 如图 b,AB 是 ⊙O 的直径,且 AB=2,C,D 是同一半圆上的两点,并且 与 的度数分别是 96° 和 36°,动点 P 是 AB 上的任意一点,则 PC+PD 的最小值是 .
A
B
C
D
P
O
图b
D`
P
例5 如图,在 Rt△ABC 中,∠ABC=90°,以 AB 为直径的 ☉O 交 AC 于点 D,连接 BD.
考点三 切线的判定与性质
解:(1) ∵AB 是直径,∴∠ADB = 90°.
∵AD = 3,BD = 4,∴AB = 5.
∵∠CDB = ∠ABC,∠A = ∠A,
∴△ADB∽△ABC,
∵ 即 ∴BC=
(1) 若 AD = 3,BD = 4,求边 BC 的长.
又∵∠OBD +∠DBC=90°,∠C +∠DBC = 90°,
∴∠C =∠OBD. ∴∠BDO =∠CDE.
∵AB 是直径,∴∠ADB = 90°.
∴∠BDC = 90°.
即∠BDE +∠CDE= 90°.
∴∠BDE+∠BDO= 90°,即∠ODE=90°.
∴ED 与☉O 相切.
(2) 证明:连接 OD,在 Rt△BDC 中,
∵E 是 BC 的中点,∴CE = DE.∴∠C =∠CDE.
又OD = OB,∴∠ODB =∠OBD.
(2) 取 BC 的中点 E,连接 ED,试证明 ED 与 ☉O 相切.
例6 (多解题)如图,直线 AB,CD 相交于点 O, ∠AOD=30°,半径为 1 cm的 ☉P 的圆心在射线 OA 上,且与点 O 的距离为 6 cm,如果 ☉P 以 1 cm/s 的速度沿由 A 向 B 的方向移动,那么 秒钟后 ☉P 与直线 CD 相切.
4 或 8
解析: 本题应分为两种情况:(1) ☉P 在直线 CD 下面与直线 CD 相切;(2) ☉P 在直线 CD 上面与直线 CD 相切.
A
B
D
C
P
P2
P1
E
o
解析: 连接 BD,则在Rt△BCD 中,BE=DE,利用角的互余证明 ∠C=∠EDC.
例7 如图,在 Rt△ABC 中,∠ABC = 90°,以 AB 为直径的 ☉O 交 AC 于点 D,过点 D 的切线交 BC 于 E.
(1) 求证:BC = 2DE.
解:(1) 证明:连接 BD,
∵AB 为直径,∠ABC = 90°,
∴BE 切 ☉O 于点 B.
又∵DE 切 ☉O 于点 D,∴DE=BE,
∴∠EBD =∠EDB.
∵∠ADB = 90°,
∴∠EBD +∠C = 90°,∠BDE +∠CDE = 90°.
∴∠C =∠CDE,DE = CE.
∴BC = BE + CE = 2DE.
(2)∵ DE = 2,∴ BC = 2DE = 4.
在 Rt△ABC 中,
∴ AB = BC =
在 Rt△ABC 中,
又∵△ABD∽△ACB,
∴ 即
∴
(2) 若 tanC= ,DE=2,求 AD 的长.
例8 如图,已知灯塔 A 的周围 7 海里的范围内有暗礁,一艘渔轮在 B 处测得灯塔 A 在北偏东 60° 的方向,向东航行 8 海里到达 C 处后,又测得该灯塔在北偏东30°的方向,如果渔轮不改变航向,继续向东航行,有没有触礁的危险?请通过计算说明理由.
(参考数据 =1.732)
B
北
60°
30°
A
C
解析:灯塔 A 的周围 7 海里都是暗礁,即表示以 A 为圆心,7 海里为半径的圆中,都是暗礁.渔轮是否会触礁,关键是看渔轮与圆心 A 之间的距离 d 的大小关系.
B
北
60°
30°
A
C
D
解:如图,作 AD 垂直于 BC 于 D,根据题意,得 BC=8.设 AD 为 x.
∵∠ABC=30°,∴AB = 2x.
BD= x.
∵∠ACD = 90° - 30°= 60°,
∴ AD=CD×tan60°,CD = .
BC=BD-CD= = 8.
解得 x=
即渔船继续往东行驶,
有触礁的危险.
B
北
60°
30°
A
C
5. 如图 b,线段 AB 是直径,点 D 是 ☉O 上一点, ∠CDB=20°,过点 C 作☉O 的切线交 AB 的延长线于点 E,则 ∠E = .
O
C
A
B
E
D
图b
50°
针对训练
6. 如图,以 △ABC 的边 AB 为直径的 ⊙O 交边 AC 于点D,且过点 D 的切线 DE 平分边 BC.
问:BC 与 ⊙O 是否相切?
解:BC 与 ⊙O 相切.理由:连接 OD,BD,
∵DE 切 ⊙O 于 D,AB 为直径,
∴∠EDO=∠ADB=90°.
又 DE 平分 CB,∴DE= BC=BE.
∴∠EDB=∠EBD.
又∠ODB=∠OBD,∠ODB+∠EDB=90°,∴∠OBD+∠DBE=90°,
即∠ABC=90°. ∴BC 与 ⊙O 相切.
例9 如图,四边形 OABC 为菱形,点 B、C 在以点 O 为圆心的圆上, OA = 1,∠AOC = 120°,∠1=∠2,求扇形 OEF 的面积?
解:∵四边形 OABC 为菱形
∴OC = OA = 1
∵ ∠AOC = 120°,∠1 =∠2
∴ ∠FOE = 120°
又∵点 C 在以点 O 为圆心的圆上
考点四 弧长与扇形面积
8. 一条弧所对的圆心角为 135°,弧长等于半径为 5 cm的圆的周长的 3 倍,则这条弧的半径为 .
40 cm
针对训练
9. 如图,在正方形 ABCD 内有一条折线段,其中AE⊥EF,EF⊥FC,已知 AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段 FC 平移到直线 AE 上,此时点 F 与点 E 重合,
点 C 到达点 C' 的位置.连接 AC,如图所示.
根据平移的方法可知,四边形 EFCC' 是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在 Rt△AC'C 中,得
∴正方形 ABCD 外接圆的半径为 .
∴正方形 ABCD 的边长为 .
例10 若一个正六边形的周长为 24,则该正六边形的面积为______.
考点五 圆内接正多边形的有关计算
10. 如图,正六边形 ABCDEF 内接于半径为 5 的 ⊙O,四边形 EFGH 是正方形.
(1) 求正方形EFGH的面积;
解:(1) ∵正六边形的边长与其半径相等,
∴EF = OF = 5.
∵四边形 EFGH 是正方形,
∴FG = EF = 5,
∴正方形EFGH的面积是 25.
针对训练
(2) ∵正六边形的边长与其半径相等,
∴∠OFE = 60°.
∵正方形的内角是 90°,
∴∠OFG =∠OFE +∠EFG = 60°+90° = 150°.
由 (1) 得 OF = FG,
∴∠OGF= (180°-∠OFG)
= (180°-150°)=15°.
(2) 连接 OF、OG,求 ∠OGF 的度数.
例11 如图,在平面直角坐标系中,⊙P 经过 x 轴上一点 C,与 y 轴分别交于 A,B 两点,连接 AP 并延长分别交 ⊙P,x 轴于点 D,E,连接 DC 并延长交 y 轴于点 F,若点 F 的坐标为(0,1),点 D 的坐标为(6,﹣1).
(1) 求证:CD = CF;
(2) 判断⊙P 与 x 轴的位置关系,
并说明理由;
(3) 求直线 AD 的函数表达式.
考点七 有关圆的综合性题目
解:(1) 证明:过点 D 作 DH⊥x 轴于H,
则∠CHD =∠COF =90°,如图所示.
∵点 F(0,1),点 D(6,-1),∴ DH = OF = 1.
∵∠FCO =∠DCH,
∴△FOC≌△DHC.
∴CD = CF.
(2) ⊙P与 x 轴相切.理由如下:
连接 CP,如图所示.
∵AP = PD,CD = CF,∴CP∥AF.
∴∠PCE = ∠AOC = 90°.
∴⊙P 与 x 轴相切.
(3) 由 (2) 可知 CP 是 △ADF 的中位线.
∴AF = 2CP.
∵AD = 2CP,
∴AD = AF.
连接 BD,如图所示.
∵AD为 ⊙P 的直径,
∴∠ABD = 90°.
∴BD = OH = 6,OB = DH = OF = 1.
设 AD = x,则 AB = AF-BF = AD-BF
= AD-(OB + OF) = x-2.
Rt△ABD 中,由勾股定理,得
AD2=AB2+BD2,即 x2 = (x-2)2 + 62,
解得 x = 10.
∴OA = AB + OB = 8 + 1 = 9. ∴点 A(0,-9).
设直线 AD 的函数表达式为 y=kx+b,
把点 A(0,-9),D(6,-1) 代入,得
解得
∴直线AD的函数表达式为 .
圆
圆的有关性质
垂径定理
添加辅助线
连半径,作弦心距(圆心到弦的距离),构造直角三角形
圆周角定理
添加辅助线
作弦,构造直径所对的圆周角
圆的概念
圆的对称性
圆
与圆有关的位置关系
与圆有关的计算
点与圆的位置关系
点在圆内:
r < d < R
直线与圆的位置的关系
添加辅助
线证切线
有公共点,连半径,证垂直;无公共点,作垂直,证半径;见切点,连半径,得垂直.
正多边形和圆
转化
直角三角形
弧长和扇形
灵活使用公式
见教材章末练习
小结与复习
第三章 圆
一、圆的基本概念及性质
1. 定义:平面上到定点的距离等于定长的所有点
组成的图形叫做圆.
2. 有关概念:
(1) 弦、直径(圆中最长的弦)
(2) 弧、优弧、劣弧、等弧
.
O
3. 不在同一条直线上的三个点确定一个圆.
二、点与圆的位置关系
●A
● B
●C
点与圆的位置关系 点到圆心的距离 d 与圆的半径 r 之间的关系
点在圆外
点在圆上
点在圆内
●O
d
r
d > r
d = r
d < r
三、圆的对称性
1. 圆是轴对称图形,经过圆心的每一条直线都是
它的对称轴.圆有无数条对称轴.
2. 圆是中心对称图形,并且绕圆心旋转任何一
个角度都能与自身重合,
即圆具有旋转不变性.
.
3.在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、
两条弦中有一组量相等,那么它们所对应的其余
各组量都分别相等.
●O
A
B
C
D
M└
③AM=BM,
若 ① CD 是直径
② CD⊥AB
可推得
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
四、垂径定理及推论
④ ,
⑤ .
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
拓展:垂径定理的逆定理
②CD⊥AB,
由 ① CD 是直径
③ AM = BM
可推得
O
C
D
A
B
●
┗
M
④ ,
⑤ .
●
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角的
一半.
五、圆周角和圆心角的关系
∠BAC = ∠BOC
C
A
B
O
推论:同弧或等弧所对的圆周角相等.
∵∠ABC 与∠ADC 、∠AEC 是同弧所对的圆周角
∴∠ABC = ∠ADC = ∠AEC
●
O
推论:直径所对的圆周角是直角;
90° 的圆周角所对的弦是圆的直径.
推论:圆的内接四边形的对角互补.
A
B
O
C
D
六、直线和圆的位置关系
图形
直线与圆的 位置关系
公共点个数
圆心到直线的距离 d 与半径 r 的关系
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
七、切线的判定与性质
1. 切线的判定一般有三种方法:
a. 定义法:和圆有唯一的一个公共点
b. 距离法: d = r
c. 判定定理:过半径的外端且垂直于半径
2. 切线的性质
圆的切线垂直于过切点的半径.
切线长定理:
过圆外一点画圆的两条切线,它们的切线长相等.
拓展:这一点和圆心的连线平分这两条切线的夹角.
切线长:
过圆外一点画圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
3.切线长及切线长定理
八、三角形的内切圆及内心
1. 与三角形各边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做三角形的内心.
3. 三角形的内心就是三角形的三条角平分线的交点.
三角形的内心到三角形的三边的距离相等.
O
C
D
A
B
M
半径 R
圆心角
弦心距 d
弦a
圆心
中心角
A
B
C
D
E
F
O
半径 R
边心距 r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
M
九、圆内接正多边形
1.正 n 边形的中心角=
C
D
O
B
E
F
A
P
3. 正 n 边形的边长 a,半径 R,边心距 r 之间的关系:
a
R
r
4. 边长 a,边心距 r 的正 n 边形面积的计算:
其中 l 为正 n 边形的周长.
2.正多边形的内角=
计算公式:
(1) 弧长公式:
(2) 扇形面积公式:
十、弧长及扇形的面积
例1 如图,在 ⊙O 中,∠ABC = 50°,则 ∠CAO
等于( )
A.30° B.40°
C.50° D.60°
B
考点一 圆的有关概念及性质
例2 在图中,BC 是 ☉O 的直径,AD⊥BC,若∠D=36°,则 ∠BAD 的度数是( )
A. 72° B. 54°
C. 45° D. 36 °
A
B
C
D
B
例3 ☉O 的半径为 r,圆心到点 A 的距离为 d,且 r、d 分别是方程 x2-6x+8=0 的两根,则点 A 与 ☉O 的位置关系是( )
A.点 A 在 ☉O 内部 B.点 A 在 ☉O 上
C.点 A 在 ☉O 外部 D.点 A 不在 ☉O 上
解析:此题需先计算出一元二次方程 x2-6x+8=0 的两个根,然后再根据R与d的之间的关系判断出点 A 与 ☉O 的关系.
D
1. 如图所示,在圆 O 中弦 AB∥CD,若 ∠ABC=50°,则 ∠BOD 等于( )
A.50° B.40° C.100° D.80°
C
针对训练
2.如图所示,四边形 ABCD 为 ☉O 的内接正方形,点 P 为劣弧 BC 上的任意一点(不与 B,C 重合),则∠BPC 的度数是 .
135°
C
D
B
A
P
O
考点二 垂径定理
例4 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是 10 mm,测得钢珠顶端离零件表面的距离为 8 mm,如图所示,则这个小圆孔的宽口 AB 的长度
为 mm.
8mm
A
B
8
C
D
O
解析:设圆心为 O,连接 AO,作出过点 O 的弓形高 CD,垂足为 D,可知AO=5 mm,OD=3 mm,利用勾股定理进行计算,AD=4 mm,所以 AB=8 mm.
3. 如图 a,点 C 是扇形 OAB 上的 的任意一点,OA=2,连接 AC,BC,过点 O 作 OE ⊥AC,OF ⊥BC,垂足分别为E,F,连接 EF,则 EF 的长度等于 .
A
O
B
C
E
F
图 a
针对训练
4. 如图 b,AB 是 ⊙O 的直径,且 AB=2,C,D 是同一半圆上的两点,并且 与 的度数分别是 96° 和 36°,动点 P 是 AB 上的任意一点,则 PC+PD 的最小值是 .
A
B
C
D
P
O
图b
D`
P
例5 如图,在 Rt△ABC 中,∠ABC=90°,以 AB 为直径的 ☉O 交 AC 于点 D,连接 BD.
考点三 切线的判定与性质
解:(1) ∵AB 是直径,∴∠ADB = 90°.
∵AD = 3,BD = 4,∴AB = 5.
∵∠CDB = ∠ABC,∠A = ∠A,
∴△ADB∽△ABC,
∵ 即 ∴BC=
(1) 若 AD = 3,BD = 4,求边 BC 的长.
又∵∠OBD +∠DBC=90°,∠C +∠DBC = 90°,
∴∠C =∠OBD. ∴∠BDO =∠CDE.
∵AB 是直径,∴∠ADB = 90°.
∴∠BDC = 90°.
即∠BDE +∠CDE= 90°.
∴∠BDE+∠BDO= 90°,即∠ODE=90°.
∴ED 与☉O 相切.
(2) 证明:连接 OD,在 Rt△BDC 中,
∵E 是 BC 的中点,∴CE = DE.∴∠C =∠CDE.
又OD = OB,∴∠ODB =∠OBD.
(2) 取 BC 的中点 E,连接 ED,试证明 ED 与 ☉O 相切.
例6 (多解题)如图,直线 AB,CD 相交于点 O, ∠AOD=30°,半径为 1 cm的 ☉P 的圆心在射线 OA 上,且与点 O 的距离为 6 cm,如果 ☉P 以 1 cm/s 的速度沿由 A 向 B 的方向移动,那么 秒钟后 ☉P 与直线 CD 相切.
4 或 8
解析: 本题应分为两种情况:(1) ☉P 在直线 CD 下面与直线 CD 相切;(2) ☉P 在直线 CD 上面与直线 CD 相切.
A
B
D
C
P
P2
P1
E
o
解析: 连接 BD,则在Rt△BCD 中,BE=DE,利用角的互余证明 ∠C=∠EDC.
例7 如图,在 Rt△ABC 中,∠ABC = 90°,以 AB 为直径的 ☉O 交 AC 于点 D,过点 D 的切线交 BC 于 E.
(1) 求证:BC = 2DE.
解:(1) 证明:连接 BD,
∵AB 为直径,∠ABC = 90°,
∴BE 切 ☉O 于点 B.
又∵DE 切 ☉O 于点 D,∴DE=BE,
∴∠EBD =∠EDB.
∵∠ADB = 90°,
∴∠EBD +∠C = 90°,∠BDE +∠CDE = 90°.
∴∠C =∠CDE,DE = CE.
∴BC = BE + CE = 2DE.
(2)∵ DE = 2,∴ BC = 2DE = 4.
在 Rt△ABC 中,
∴ AB = BC =
在 Rt△ABC 中,
又∵△ABD∽△ACB,
∴ 即
∴
(2) 若 tanC= ,DE=2,求 AD 的长.
例8 如图,已知灯塔 A 的周围 7 海里的范围内有暗礁,一艘渔轮在 B 处测得灯塔 A 在北偏东 60° 的方向,向东航行 8 海里到达 C 处后,又测得该灯塔在北偏东30°的方向,如果渔轮不改变航向,继续向东航行,有没有触礁的危险?请通过计算说明理由.
(参考数据 =1.732)
B
北
60°
30°
A
C
解析:灯塔 A 的周围 7 海里都是暗礁,即表示以 A 为圆心,7 海里为半径的圆中,都是暗礁.渔轮是否会触礁,关键是看渔轮与圆心 A 之间的距离 d 的大小关系.
B
北
60°
30°
A
C
D
解:如图,作 AD 垂直于 BC 于 D,根据题意,得 BC=8.设 AD 为 x.
∵∠ABC=30°,∴AB = 2x.
BD= x.
∵∠ACD = 90° - 30°= 60°,
∴ AD=CD×tan60°,CD = .
BC=BD-CD= = 8.
解得 x=
即渔船继续往东行驶,
有触礁的危险.
B
北
60°
30°
A
C
5. 如图 b,线段 AB 是直径,点 D 是 ☉O 上一点, ∠CDB=20°,过点 C 作☉O 的切线交 AB 的延长线于点 E,则 ∠E = .
O
C
A
B
E
D
图b
50°
针对训练
6. 如图,以 △ABC 的边 AB 为直径的 ⊙O 交边 AC 于点D,且过点 D 的切线 DE 平分边 BC.
问:BC 与 ⊙O 是否相切?
解:BC 与 ⊙O 相切.理由:连接 OD,BD,
∵DE 切 ⊙O 于 D,AB 为直径,
∴∠EDO=∠ADB=90°.
又 DE 平分 CB,∴DE= BC=BE.
∴∠EDB=∠EBD.
又∠ODB=∠OBD,∠ODB+∠EDB=90°,∴∠OBD+∠DBE=90°,
即∠ABC=90°. ∴BC 与 ⊙O 相切.
例9 如图,四边形 OABC 为菱形,点 B、C 在以点 O 为圆心的圆上, OA = 1,∠AOC = 120°,∠1=∠2,求扇形 OEF 的面积?
解:∵四边形 OABC 为菱形
∴OC = OA = 1
∵ ∠AOC = 120°,∠1 =∠2
∴ ∠FOE = 120°
又∵点 C 在以点 O 为圆心的圆上
考点四 弧长与扇形面积
8. 一条弧所对的圆心角为 135°,弧长等于半径为 5 cm的圆的周长的 3 倍,则这条弧的半径为 .
40 cm
针对训练
9. 如图,在正方形 ABCD 内有一条折线段,其中AE⊥EF,EF⊥FC,已知 AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段 FC 平移到直线 AE 上,此时点 F 与点 E 重合,
点 C 到达点 C' 的位置.连接 AC,如图所示.
根据平移的方法可知,四边形 EFCC' 是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在 Rt△AC'C 中,得
∴正方形 ABCD 外接圆的半径为 .
∴正方形 ABCD 的边长为 .
例10 若一个正六边形的周长为 24,则该正六边形的面积为______.
考点五 圆内接正多边形的有关计算
10. 如图,正六边形 ABCDEF 内接于半径为 5 的 ⊙O,四边形 EFGH 是正方形.
(1) 求正方形EFGH的面积;
解:(1) ∵正六边形的边长与其半径相等,
∴EF = OF = 5.
∵四边形 EFGH 是正方形,
∴FG = EF = 5,
∴正方形EFGH的面积是 25.
针对训练
(2) ∵正六边形的边长与其半径相等,
∴∠OFE = 60°.
∵正方形的内角是 90°,
∴∠OFG =∠OFE +∠EFG = 60°+90° = 150°.
由 (1) 得 OF = FG,
∴∠OGF= (180°-∠OFG)
= (180°-150°)=15°.
(2) 连接 OF、OG,求 ∠OGF 的度数.
例11 如图,在平面直角坐标系中,⊙P 经过 x 轴上一点 C,与 y 轴分别交于 A,B 两点,连接 AP 并延长分别交 ⊙P,x 轴于点 D,E,连接 DC 并延长交 y 轴于点 F,若点 F 的坐标为(0,1),点 D 的坐标为(6,﹣1).
(1) 求证:CD = CF;
(2) 判断⊙P 与 x 轴的位置关系,
并说明理由;
(3) 求直线 AD 的函数表达式.
考点七 有关圆的综合性题目
解:(1) 证明:过点 D 作 DH⊥x 轴于H,
则∠CHD =∠COF =90°,如图所示.
∵点 F(0,1),点 D(6,-1),∴ DH = OF = 1.
∵∠FCO =∠DCH,
∴△FOC≌△DHC.
∴CD = CF.
(2) ⊙P与 x 轴相切.理由如下:
连接 CP,如图所示.
∵AP = PD,CD = CF,∴CP∥AF.
∴∠PCE = ∠AOC = 90°.
∴⊙P 与 x 轴相切.
(3) 由 (2) 可知 CP 是 △ADF 的中位线.
∴AF = 2CP.
∵AD = 2CP,
∴AD = AF.
连接 BD,如图所示.
∵AD为 ⊙P 的直径,
∴∠ABD = 90°.
∴BD = OH = 6,OB = DH = OF = 1.
设 AD = x,则 AB = AF-BF = AD-BF
= AD-(OB + OF) = x-2.
Rt△ABD 中,由勾股定理,得
AD2=AB2+BD2,即 x2 = (x-2)2 + 62,
解得 x = 10.
∴OA = AB + OB = 8 + 1 = 9. ∴点 A(0,-9).
设直线 AD 的函数表达式为 y=kx+b,
把点 A(0,-9),D(6,-1) 代入,得
解得
∴直线AD的函数表达式为 .
圆
圆的有关性质
垂径定理
添加辅助线
连半径,作弦心距(圆心到弦的距离),构造直角三角形
圆周角定理
添加辅助线
作弦,构造直径所对的圆周角
圆的概念
圆的对称性
圆
与圆有关的位置关系
与圆有关的计算
点与圆的位置关系
点在圆内:
r < d < R
直线与圆的位置的关系
添加辅助
线证切线
有公共点,连半径,证垂直;无公共点,作垂直,证半径;见切点,连半径,得垂直.
正多边形和圆
转化
直角三角形
弧长和扇形
灵活使用公式
见教材章末练习
