第三章 圆章末复习课件(共38张PPT)-2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 第三章 圆章末复习课件(共38张PPT)-2024-2025学年北师大版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 00:00:00 | ||
图片预览






文档简介
(共38张PPT)
北师版·九年级下册
章末复习
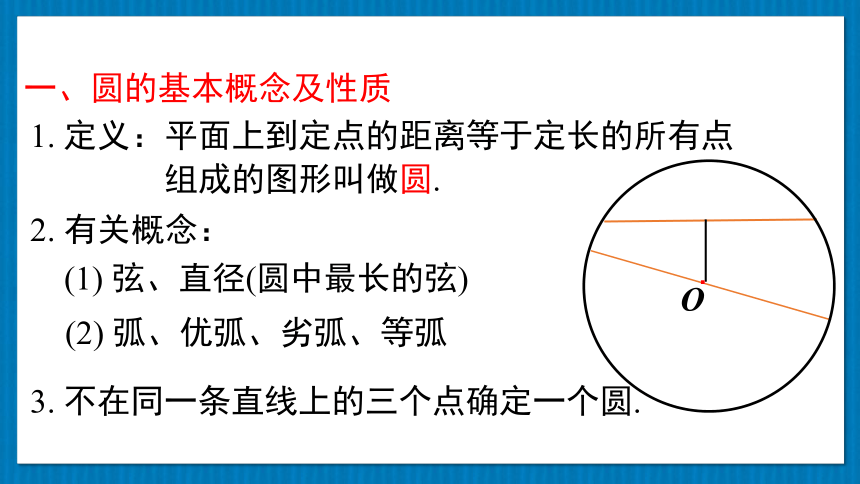
一、圆的基本概念及性质
1. 定义:平面上到定点的距离等于定长的所有点
组成的图形叫做圆.
2. 有关概念:
(1) 弦、直径(圆中最长的弦)
(2) 弧、优弧、劣弧、等弧
.
O
3. 不在同一条直线上的三个点确定一个圆.
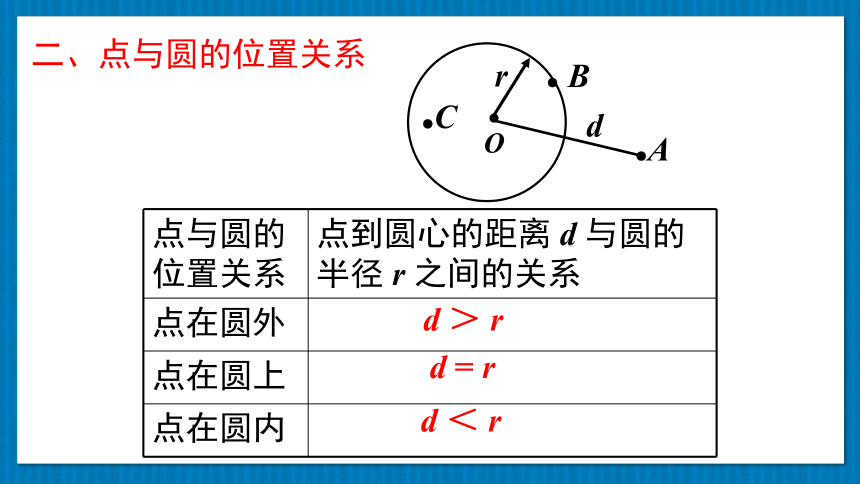
二、点与圆的位置关系
●A
● B
●C
点与圆的位置关系 点到圆心的距离 d 与圆的半径 r 之间的关系
点在圆外
点在圆上
点在圆内
●O
d
r
d > r
d = r
d < r
知识梳理
圆的对称性
圆是 对称图形,任何一条直径所在的直线都是它的 ;圆又是 对称图形,_____ 是它的对称中心.
O
轴
对称轴
中心
圆心
并且绕圆心旋转任何一个
角度都能与自身重合,
即圆具有旋转不变性.
●O
A
B
C
D
M└
③AM=BM,
若 ① CD 是直径
② CD⊥AB
可推得
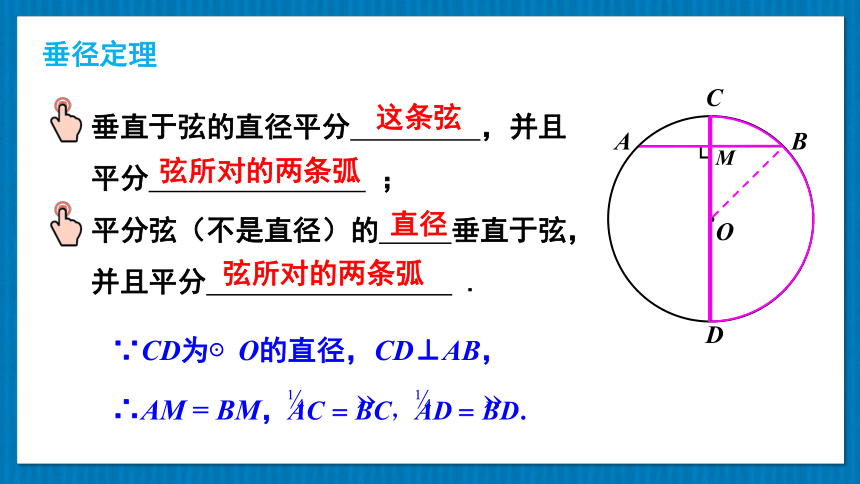
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理及推论
④ ,
⑤ .
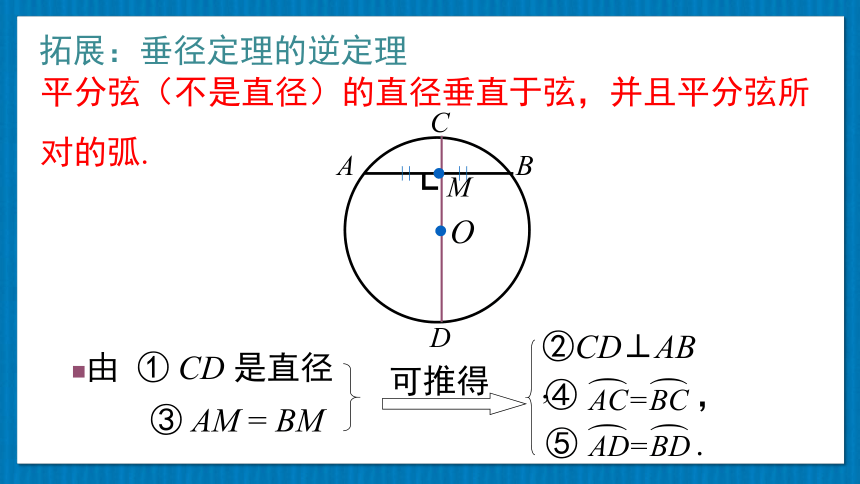
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
拓展:垂径定理的逆定理
②CD⊥AB,
由 ① CD 是直径
③ AM = BM
可推得
O
C
D
A
B
●
┗
M
④ ,
⑤ .
●
垂径定理
这条弦
弦所对的两条弧
直径
弦所对的两条弧
C
D
A
B
M
O
垂直于弦的直径平分 ,并且平分 ;
平分弦(不是直径)的 垂直于弦,并且平分 .
∵CD为⊙O的直径,CD⊥AB,
∴AM = BM,
圆心角、弧、弦的关系
在同圆或等圆中,相等的圆心角所对的 相等,所对的 相等.
弧
弦
在同圆或等圆中,如果两个_______,两条____,两条____,中有一组量______,那么它们所对应的其余各组量都分别_______.
O
A
B
A′
B′
圆心角
弧
弦
相等
相等
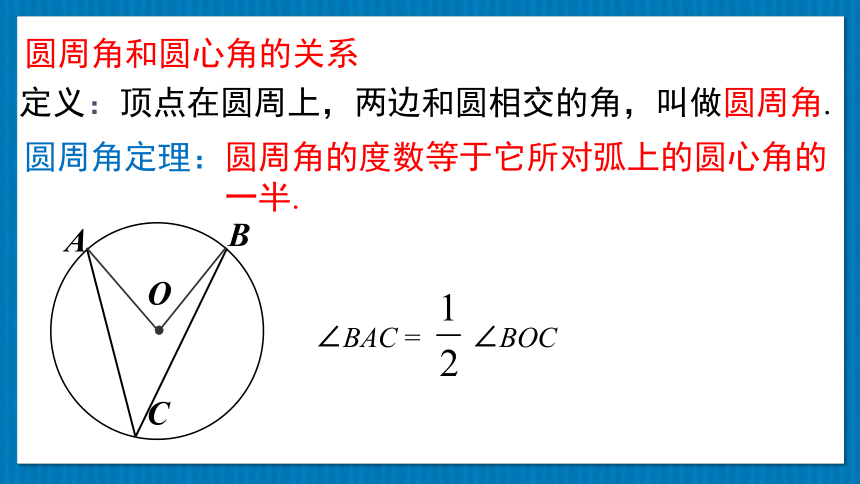
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角的
一半.
圆周角和圆心角的关系
∠BAC = ∠BOC
C
A
B
O
推论:同弧或等弧所对的圆周角相等.
∵∠ABC 与∠ADC 、∠AEC 是同弧所对的圆周角
∴∠ABC = ∠ADC = ∠AEC
●
O
推论:直径所对的圆周角是直角;
90° 的圆周角所对的弦是圆的直径.
推论:圆的内接四边形的对角互补.
A
B
O
C
D
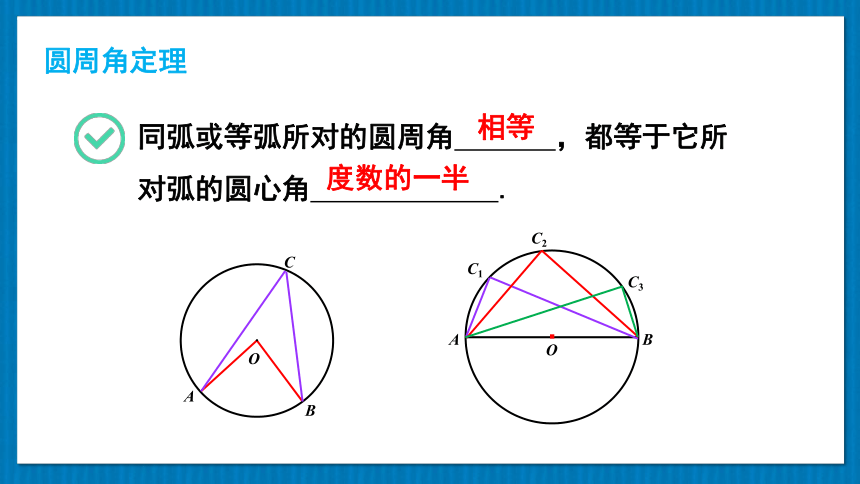
圆周角定理
同弧或等弧所对的圆周角 ,都等于它所对弧的圆心角 .
·
A
C
B
O
·
A
C1
O
C2
C3
B
相等
度数的一半
圆周角定理
·
A
C
B
O
·
A
C1
O
C2
C3
B
直径所对的圆周角是 ,90°所对的弦是 .
直角
直径
直线和圆的位置关系
图形
直线与圆的 位置关系
公共点个数
圆心到直线的距离 d 与半径 r 的关系
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
与圆有关的位置关系
r
·
O
A
P
P
P
圆外
圆上
圆内
>
=
<
·
l
O
r
l
l
相交
相切
相离
(1) 点与圆的位置关系
① d r
② d r
③ d r
(2)直线与圆的位置关系
① d r
② d r
③ d r
<
=
>
切线的判定与性质
1. 切线的判定一般有三种方法:
a. 定义法:和圆有唯一的一个公共点
b. 距离法: d = r
c. 判定定理:过半径的外端且垂直于半径
2. 切线的性质
圆的切线垂直于过切点的半径.
圆的切线的性质
圆的切线 过切点的半径.
垂直于
∵l是⊙O的切线,切点为A,OA是⊙O的直径,
∴OA⊥l.
·
O
l
A
圆的切线的判定
经过________的外端,并且________这条________的直线是圆的切线.
·
O
A
l
半径
垂直于
半径
∵OA是⊙O的半径, l⊥OA于A,
∴ l是⊙O的切线.
切线长定理:
过圆外一点画圆的两条切线,它们的切线长相等.
拓展:这一点和圆心的连线平分这两条切线的夹角.
切线长:
过圆外一点画圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
切线长及切线长定理
切线长定理
A
P
O
.
B
从圆外一点所画的圆的两条切线的长相等.
∵PA、PB分别切⊙O于A、B,
∴PA=PB,∠BPO=∠APO.
圆的内接多边形
A
B
C
D
圆的内接四边形对角互补
圆的内接正多边形
三角形的内切圆及内心
1. 与三角形各边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做三角形的内心.
3. 三角形的内心就是三角形的三条角平分线的交点.
三角形的内心到三角形的三边的距离相等.
O
C
D
A
B
M
半径 R
圆心角
弦心距 d
弦a
圆心
中心角
A
B
C
D
E
F
O
半径 R
边心距 r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
M
圆内接正多边形
1.正 n 边形的中心角=
C
D
O
B
E
F
A
P
3. 正 n 边形的边长 a,半径 R,边心距 r 之间的关系:
a
R
r
4. 边长 a,边心距 r 的正 n 边形面积的计算:
其中 l 为正 n 边形的周长.
2.正多边形的内角=
计算公式:
(1) 弧长公式:
(2) 扇形面积公式:
弧长及扇形的面积
弧长与扇形面积的计算
n°的圆心角所对的弧长计算公式为 .
n°的圆心角所在的扇形面积为 .
随堂练习
1.如图,⊙O是△ABC的外接圆,已知∠ACO=30°,∠B=_______.
B
A
O
C
方法一:连接OA
30°
方法二:延长CO交⊙O于D,连接DA
60°
D
2. 如图,在⊙O中,弦AB=1.8cm,圆周角∠ACB=30°,则⊙O的直径等于______cm.
B
C
O
A
D
3.6
连接AO,并延长交⊙O于D,连接BD,
∴∠D=∠C=30° ,
∵AD是直径,∴∠B=90° ,
3. 已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
O
A
B
C
D
E
F
O
A
B
C
D
E
F
证明:连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.即∠OAE=∠OBF.
∴在△OAE与△OBF中,
∴△OAE≌△OBF(SAS).
∴OE=OF.
O
A
B
C
D
E
F
解:OE=OF ,
方法一
解:OE=OF ,
方法二
O
A
B
C
D
E
F
G
证明:从圆心O向弦AB作垂线交于点G,
∵OG⊥AB,
∴AG=BG.
∵AE=BF ,AG=AE+EG ,BG=BF+FG
∴EG=FG.
∴G点为EF的中点
又∵OG⊥EF,
∴OG为EF 的垂直平分线
∴△OEF为等腰三角形.
∴OE=OF.
4. 某酒店大堂要铺设圆环形地毯,如图,工人王师傅只测量了与小圆相切的大圆的弦AB的长就计算出了圆环的面积,王师傅是怎样算的?请你用圆的相关知识加以解释.
O
A
B
C
解:连接圆心O与切点C,连接AO ,
∵OC⊥AB,
∴在△AOC中,AO2-OC2=AC2,
∴S圆环面积=π(AO2-OC2)=πAC2.
5. 如图,过圆外一点O作⊙O′的两条切线OA、OB,A、B是切点,且OO′是圆O′半径长两倍,则∠AOB=______
60 °
O
A
B
O′
6. 如图,Rt△ABC内接于⊙O,∠A=30°,延长斜边AB到D,使BD等于⊙O半径,求证:DC是⊙O切线.
O
A
B
C
D
证明:连OC,如图,
∵∠A=30°,OA=OC,
∴∠COB=60°,
∴△COB为等边三角形,
∴BC=BO,
而BD等于⊙O半径,
∴BC=BO=BD,
∴△OCD为直角三角形,即∠OCD=90°,
所以DC是⊙O切线.
B
A
D
O
C
7. 如图,已知⊙O的直径AB=2,∠ABC=30°,BC= ,D是BC的中点,试判断点D与⊙O的位置关系.
请判断以下解题过程正确吗?
错误,因为不能确定∠ADB是圆周角.
解:连接OD、AD,
∵AB是直径, ∴∠ADB=90 .
∵AO=BO,
∴点D在圆上.
7. 如图,已知⊙O的直径AB=2,∠ABC=30°,BC= ,D是BC的中点,试判断点D与⊙O的位置关系.
B
A
D
O
C
解:连接OD,作OF⊥BC于点F.
∴OD=OB,点D在圆上.
F
课堂小结
《圆》的内容综合性较强,在具体应用中,进一步完善知识体系构建.
课后作业
复习题
北师版·九年级下册
章末复习
一、圆的基本概念及性质
1. 定义:平面上到定点的距离等于定长的所有点
组成的图形叫做圆.
2. 有关概念:
(1) 弦、直径(圆中最长的弦)
(2) 弧、优弧、劣弧、等弧
.
O
3. 不在同一条直线上的三个点确定一个圆.
二、点与圆的位置关系
●A
● B
●C
点与圆的位置关系 点到圆心的距离 d 与圆的半径 r 之间的关系
点在圆外
点在圆上
点在圆内
●O
d
r
d > r
d = r
d < r
知识梳理
圆的对称性
圆是 对称图形,任何一条直径所在的直线都是它的 ;圆又是 对称图形,_____ 是它的对称中心.
O
轴
对称轴
中心
圆心
并且绕圆心旋转任何一个
角度都能与自身重合,
即圆具有旋转不变性.
●O
A
B
C
D
M└
③AM=BM,
若 ① CD 是直径
② CD⊥AB
可推得
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理及推论
④ ,
⑤ .
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
拓展:垂径定理的逆定理
②CD⊥AB,
由 ① CD 是直径
③ AM = BM
可推得
O
C
D
A
B
●
┗
M
④ ,
⑤ .
●
垂径定理
这条弦
弦所对的两条弧
直径
弦所对的两条弧
C
D
A
B
M
O
垂直于弦的直径平分 ,并且平分 ;
平分弦(不是直径)的 垂直于弦,并且平分 .
∵CD为⊙O的直径,CD⊥AB,
∴AM = BM,
圆心角、弧、弦的关系
在同圆或等圆中,相等的圆心角所对的 相等,所对的 相等.
弧
弦
在同圆或等圆中,如果两个_______,两条____,两条____,中有一组量______,那么它们所对应的其余各组量都分别_______.
O
A
B
A′
B′
圆心角
弧
弦
相等
相等
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角的
一半.
圆周角和圆心角的关系
∠BAC = ∠BOC
C
A
B
O
推论:同弧或等弧所对的圆周角相等.
∵∠ABC 与∠ADC 、∠AEC 是同弧所对的圆周角
∴∠ABC = ∠ADC = ∠AEC
●
O
推论:直径所对的圆周角是直角;
90° 的圆周角所对的弦是圆的直径.
推论:圆的内接四边形的对角互补.
A
B
O
C
D
圆周角定理
同弧或等弧所对的圆周角 ,都等于它所对弧的圆心角 .
·
A
C
B
O
·
A
C1
O
C2
C3
B
相等
度数的一半
圆周角定理
·
A
C
B
O
·
A
C1
O
C2
C3
B
直径所对的圆周角是 ,90°所对的弦是 .
直角
直径
直线和圆的位置关系
图形
直线与圆的 位置关系
公共点个数
圆心到直线的距离 d 与半径 r 的关系
2 个
1 个
0 个
相离
相切
相交
d>r
d = r
d<r
与圆有关的位置关系
r
·
O
A
P
P
P
圆外
圆上
圆内
>
=
<
·
l
O
r
l
l
相交
相切
相离
(1) 点与圆的位置关系
① d r
② d r
③ d r
(2)直线与圆的位置关系
① d r
② d r
③ d r
<
=
>
切线的判定与性质
1. 切线的判定一般有三种方法:
a. 定义法:和圆有唯一的一个公共点
b. 距离法: d = r
c. 判定定理:过半径的外端且垂直于半径
2. 切线的性质
圆的切线垂直于过切点的半径.
圆的切线的性质
圆的切线 过切点的半径.
垂直于
∵l是⊙O的切线,切点为A,OA是⊙O的直径,
∴OA⊥l.
·
O
l
A
圆的切线的判定
经过________的外端,并且________这条________的直线是圆的切线.
·
O
A
l
半径
垂直于
半径
∵OA是⊙O的半径, l⊥OA于A,
∴ l是⊙O的切线.
切线长定理:
过圆外一点画圆的两条切线,它们的切线长相等.
拓展:这一点和圆心的连线平分这两条切线的夹角.
切线长:
过圆外一点画圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
切线长及切线长定理
切线长定理
A
P
O
.
B
从圆外一点所画的圆的两条切线的长相等.
∵PA、PB分别切⊙O于A、B,
∴PA=PB,∠BPO=∠APO.
圆的内接多边形
A
B
C
D
圆的内接四边形对角互补
圆的内接正多边形
三角形的内切圆及内心
1. 与三角形各边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做三角形的内心.
3. 三角形的内心就是三角形的三条角平分线的交点.
三角形的内心到三角形的三边的距离相等.
O
C
D
A
B
M
半径 R
圆心角
弦心距 d
弦a
圆心
中心角
A
B
C
D
E
F
O
半径 R
边心距 r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
M
圆内接正多边形
1.正 n 边形的中心角=
C
D
O
B
E
F
A
P
3. 正 n 边形的边长 a,半径 R,边心距 r 之间的关系:
a
R
r
4. 边长 a,边心距 r 的正 n 边形面积的计算:
其中 l 为正 n 边形的周长.
2.正多边形的内角=
计算公式:
(1) 弧长公式:
(2) 扇形面积公式:
弧长及扇形的面积
弧长与扇形面积的计算
n°的圆心角所对的弧长计算公式为 .
n°的圆心角所在的扇形面积为 .
随堂练习
1.如图,⊙O是△ABC的外接圆,已知∠ACO=30°,∠B=_______.
B
A
O
C
方法一:连接OA
30°
方法二:延长CO交⊙O于D,连接DA
60°
D
2. 如图,在⊙O中,弦AB=1.8cm,圆周角∠ACB=30°,则⊙O的直径等于______cm.
B
C
O
A
D
3.6
连接AO,并延长交⊙O于D,连接BD,
∴∠D=∠C=30° ,
∵AD是直径,∴∠B=90° ,
3. 已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
O
A
B
C
D
E
F
O
A
B
C
D
E
F
证明:连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.即∠OAE=∠OBF.
∴在△OAE与△OBF中,
∴△OAE≌△OBF(SAS).
∴OE=OF.
O
A
B
C
D
E
F
解:OE=OF ,
方法一
解:OE=OF ,
方法二
O
A
B
C
D
E
F
G
证明:从圆心O向弦AB作垂线交于点G,
∵OG⊥AB,
∴AG=BG.
∵AE=BF ,AG=AE+EG ,BG=BF+FG
∴EG=FG.
∴G点为EF的中点
又∵OG⊥EF,
∴OG为EF 的垂直平分线
∴△OEF为等腰三角形.
∴OE=OF.
4. 某酒店大堂要铺设圆环形地毯,如图,工人王师傅只测量了与小圆相切的大圆的弦AB的长就计算出了圆环的面积,王师傅是怎样算的?请你用圆的相关知识加以解释.
O
A
B
C
解:连接圆心O与切点C,连接AO ,
∵OC⊥AB,
∴在△AOC中,AO2-OC2=AC2,
∴S圆环面积=π(AO2-OC2)=πAC2.
5. 如图,过圆外一点O作⊙O′的两条切线OA、OB,A、B是切点,且OO′是圆O′半径长两倍,则∠AOB=______
60 °
O
A
B
O′
6. 如图,Rt△ABC内接于⊙O,∠A=30°,延长斜边AB到D,使BD等于⊙O半径,求证:DC是⊙O切线.
O
A
B
C
D
证明:连OC,如图,
∵∠A=30°,OA=OC,
∴∠COB=60°,
∴△COB为等边三角形,
∴BC=BO,
而BD等于⊙O半径,
∴BC=BO=BD,
∴△OCD为直角三角形,即∠OCD=90°,
所以DC是⊙O切线.
B
A
D
O
C
7. 如图,已知⊙O的直径AB=2,∠ABC=30°,BC= ,D是BC的中点,试判断点D与⊙O的位置关系.
请判断以下解题过程正确吗?
错误,因为不能确定∠ADB是圆周角.
解:连接OD、AD,
∵AB是直径, ∴∠ADB=90 .
∵AO=BO,
∴点D在圆上.
7. 如图,已知⊙O的直径AB=2,∠ABC=30°,BC= ,D是BC的中点,试判断点D与⊙O的位置关系.
B
A
D
O
C
解:连接OD,作OF⊥BC于点F.
∴OD=OB,点D在圆上.
F
课堂小结
《圆》的内容综合性较强,在具体应用中,进一步完善知识体系构建.
课后作业
复习题
