人教版九年级数学下名师点拨与训练第28章 锐角三角函数28.2 解直角三角形(含解析)
文档属性
| 名称 | 人教版九年级数学下名师点拨与训练第28章 锐角三角函数28.2 解直角三角形(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 21:11:12 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
28.2 解直角三角形
学习目标:
1 理解直角三角形中除直角以外的五个元素之间的关系.
2 能综合运用勾股定理、直角三角形两个锐角互余及锐角三角函数解直角三角形.
老师告诉你
一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
直角三角形中(1)三边关系:a2+b2=c2(勾股定理)
(2)两锐角的关系:∠A+∠B=90°
(3)边角之间的关系:
,,,
,,.
一、知识点拨
知识点1、 解直角三角形
在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.
设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).
②锐角之间的关系:∠A+∠B=90°.
③边角之间的关系:
,,,
,,.
④,h为斜边上的高.
注意:(1)直角三角形中有一个元素为定值(直角为90°),是已知值.
(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).
(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.
【新知导学】
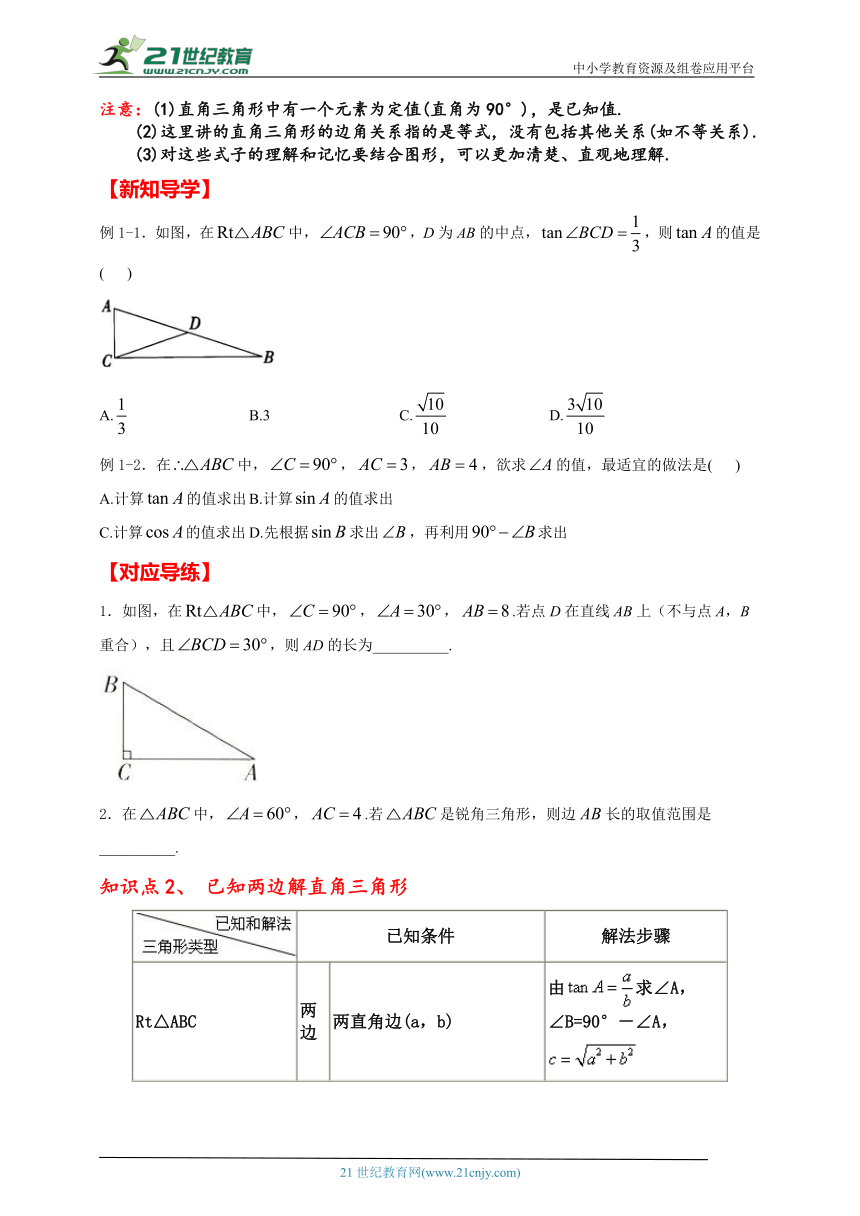
例1-1.如图,在中,,D为AB的中点,,则的值是( )
A. B.3 C. D.
例1-2.在中,,,,欲求的值,最适宜的做法是( )
A.计算的值求出 B.计算的值求出
C.计算的值求出 D.先根据求出,再利用求出
【对应导练】
1.如图,在中,,,.若点D在直线AB上(不与点A,B重合),且,则AD的长为__________.
2.在中,,.若是锐角三角形,则边长的取值范围是__________.
知识点2、 已知两边解直角三角形
已知条件 解法步骤
Rt△ABC
两
边 两直角边(a,b) 由求∠A,
∠B=90°-∠A,
斜边,一直角边(如c,a) 由求∠A,
∠B=90°-∠A,
【新知导学】
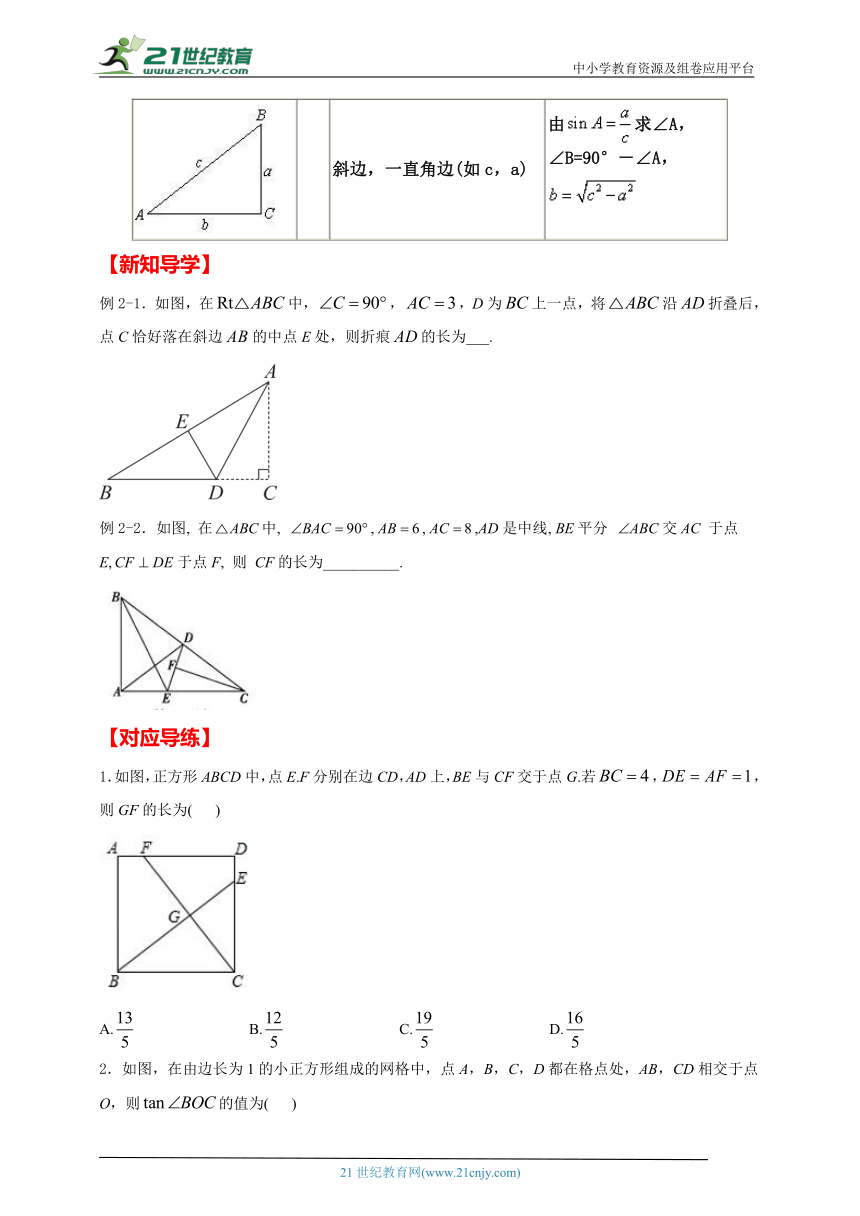
例2-1.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
例2-2.如图, 在中, ,,,AD是中线, BE平分 交AC 于点 E,于点F, 则 CF的长为__________.
【对应导练】
1.如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若,,则GF的长为( )
A. B. C. D.
2.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点处,AB,CD相交于点O,则的值为( )
A.2 B. C.3 D.
知识点3、 已知一边一锐角解直角三角形
一
边
一
角 一直角边
和一锐角 锐角、邻边
(如∠A,b) ∠B=90°-∠A,
,
锐角、对边
(如∠A,a) ∠B=90°-∠A,
,
斜边、锐角(如c,∠A) ∠B=90°-∠A,
,
【新知导学】
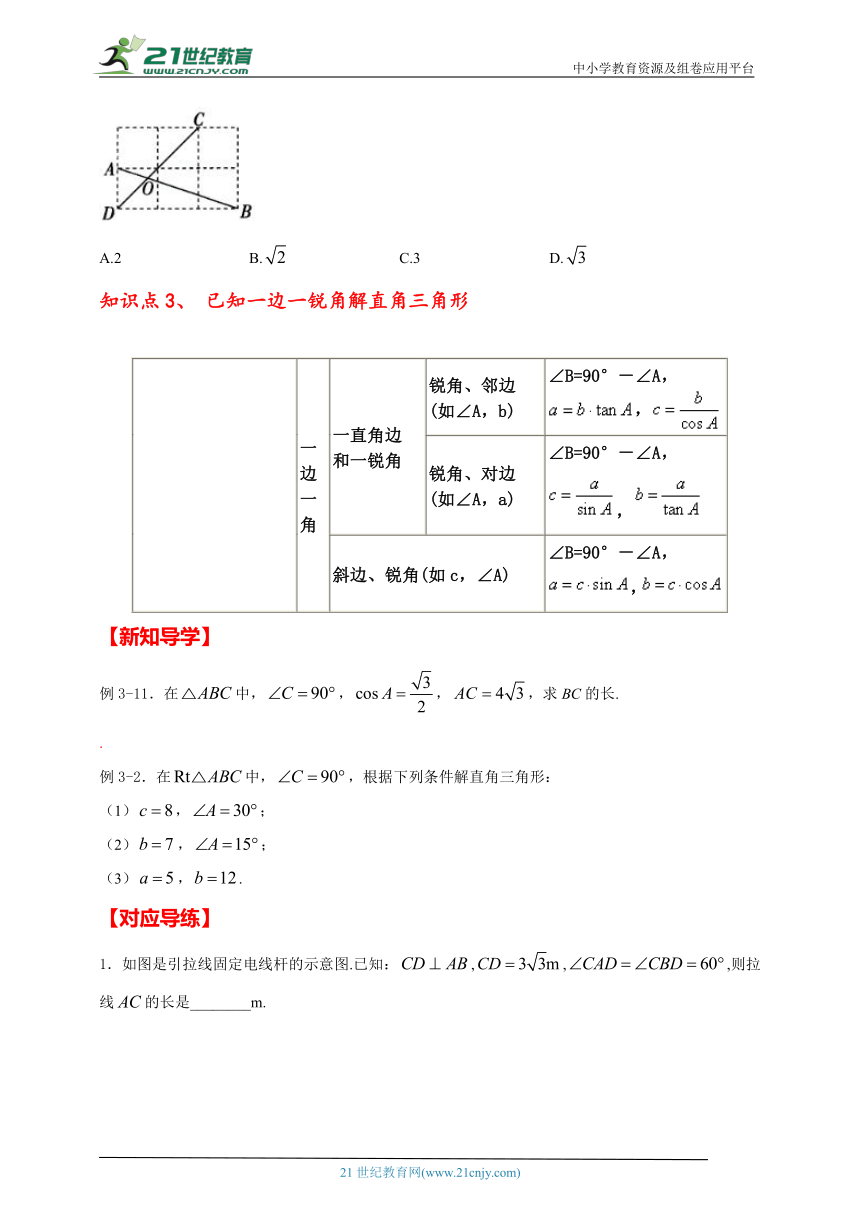
例3-11.在中,,,,求BC的长.
.
例3-2.在中,,根据下列条件解直角三角形:
(1),;
(2),;
(3),.
【对应导练】
1.如图是引拉线固定电线杆的示意图.已知:,,,则拉线的长是________m.
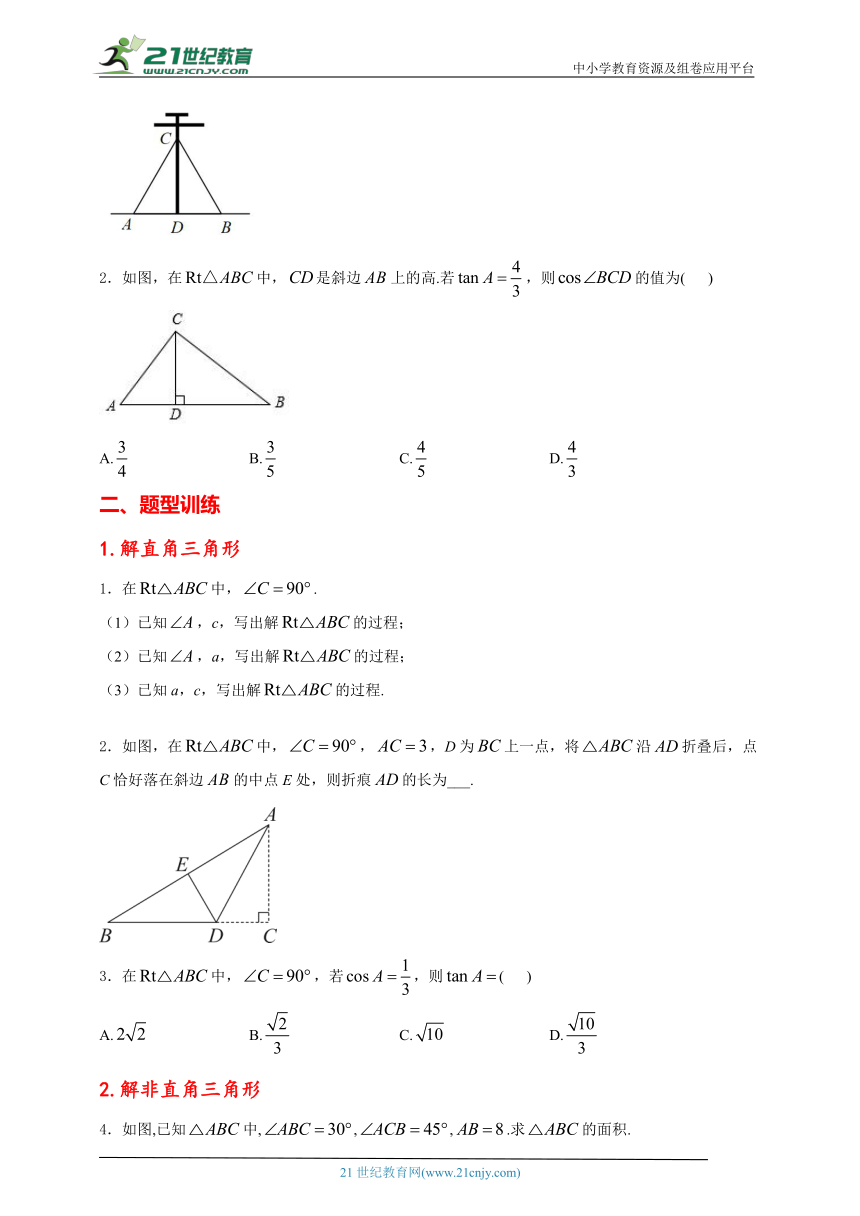
2.如图,在中,是斜边上的高.若,则的值为( )
A. B. C. D.
二、题型训练
1.解直角三角形
1.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
2.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
3.在中,,若,则( )
A. B. C. D.
2.解非直角三角形
4.如图,已知中,,,.求的面积.
5.如图,在中,AD是BC边上的高,.
(1)求证:;
(2)若,,求的面积.
6.在中,是BC边上的高,,则BC的长为_______.
3.构造直角三角形解决问题
7.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则_______.
8.如图,在小山的东侧A点处有一个热气球,由于受风向的影响,该热气球以每分钟30米的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,求A,B两点间的距离.
9.如图,在矩形ABCD中,点E为矩形内一点,且,,,,则四边形ABCE的面积是_________.
三、课堂达标
一、单选题(每小题4分,共32分)
1.如图,在中,已知,,则的长为( )
A. B. C. D.
2.在中,,,,则的长为( )
A. B. C. D.
3.在中,,若,则的值是( )
A. B. C. D.
4.如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米.
A. B. C. D.
5.在中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
6.在中,,如果,,那么等于( )
A. B. C. D.
7.如图,斜坡的坡度,那么的值为( )
A.
B.
C.
D.
8.如图,直线l:分别与x轴、y轴交于点A、B.点P为直线l在第一象限的点.作的外接圆,延长交于点D,当的面积最小时,则的半径长为( )
A. B.2 C. D.3
二、填空题(每小题4分,共20分)
9.在中,已知,,,点M在边上,点N在边上,且,连接,当为等腰三角形时,______.
10.在中,是BC边上的高,,则BC的长为_______.
11.如图,在中,,,D为上一点,且满足,过D作交延长线于点E,则_________.
12.如图,在中,,,,将绕点A逆时针旋转得到,使点C落在边上,
(1)旋转角的度数是________.
(2)线段扫过部分的面积为_________;(结果保留)
13.一副直角三角板如图放置,点C在的延长线上,,,,,,则________.
三、解答题(每小题8分,共48分)
14.在中,,,,求BC的长.
.
15.如图, 中, ,是的高, ,,求的长.
16.如图,在中,,的周长为24,,点D为的中点.求、的长.
17.阅读与思考.
请仔细阅读并完成相应的任务.
利用我们所学习的三角函数的相关知识可以解决许多关于三角形边长、角度、面积等问题.如图,在锐角中,,,的对边分别是a,b,c过点B作于点H,则,即,于是.在中,,在中,,,整理得.
任务:
(1)________,________;
(2)已知中,,,的对边分别是a,b,c,,,,求c.
18.如图①,已知在中,,,,D是斜边AB的中点.
(1)求CD的长;
(2)如图②,过点D作AB的垂线交AC于点E,求DE的长;
(3)如图③,过点A作CD的垂线,垂足为M,求的值.
19.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
28.2 解直角三角形
学习目标:
1 理解直角三角形中除直角以外的五个元素之间的关系.
2 能综合运用勾股定理、直角三角形两个锐角互余及锐角三角函数解直角三角形.
老师告诉你
一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
直角三角形中(1)三边关系:a2+b2=c2(勾股定理)
(2)两锐角的关系:∠A+∠B=90°
(3)边角之间的关系:
,,,
,,.
一、知识点拨
知识点1、 解直角三角形
在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.
设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).
②锐角之间的关系:∠A+∠B=90°.
③边角之间的关系:
,,,
,,.
④,h为斜边上的高.
注意:(1)直角三角形中有一个元素为定值(直角为90°),是已知值.
(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).
(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.
【新知导学】
例1-1.如图,在中,,D为AB的中点,,则的值是( )
A. B.3 C. D.
答案:B
解析:D为AB的中点,所以∠BCD=∠B = =
所以= =3
故选B
例1-2.在中,,,,欲求的值,最适宜的做法是( )
A.计算的值求出 B.计算的值求出
C.计算的值求出 D.先根据求出,再利用求出
答案:C
解析:根据“锐角三角函数”的定义可知,在中,当,,时,求、中的任何一个,都需要先求出BC的长;虽可直接由算出,但在求出后还需利用直角三角形中两锐角互余才能求出;而由:得到的值后就可直接求得的值了,所以C的方法更合适.
故选:C.
【对应导练】
1.如图,在中,,,.若点D在直线AB上(不与点A,B重合),且,则AD的长为__________.
答案:6或12
解析:在,,,,
当点D在点B左上方时,如图所示,
,
,
.
,
,
.
当点D在点B的右下方时,如图所示,
,,,
在中,,
,
综上所述,AD的长为6或12.故答案为:6或12.
2.在中,,.若是锐角三角形,则边长的取值范围是__________.
答案:
解析:如图,作的高,,
是锐角三角形,
,在的内部,
,,
在中,,,
,
,
又,
,
故答案为:.
知识点2、 已知两边解直角三角形
已知条件 解法步骤
Rt△ABC
两
边 两直角边(a,b) 由求∠A,
∠B=90°-∠A,
斜边,一直角边(如c,a) 由求∠A,
∠B=90°-∠A,
【新知导学】
例2-1.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
答案:
解析:方法一:将沿折叠后,点C恰好落在斜边的中点E处,
,,,
,,
.
又,
,
,
.
方法二:在中,,
设,则,
.
在中,,
即,
解得,
即.
故答案为:.
例2-2.如图, 在中, ,,,AD是中线, BE平分 交AC 于点 E,于点F, 则 CF的长为__________.
答案:
解析:在 中, ,,,. 如图,
过点E 作 于点G, 则,
,,
AD 是中线,,,,
,
,
【对应导练】
1.如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若,,则GF的长为( )
A. B. C. D.
答案:A
解析:正方形ABCD中,,
,,
,
,
,
在和中,
,
,
,
,
,
,
故选:A.
2.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点处,AB,CD相交于点O,则的值为( )
A.2 B. C.3 D.
答案:A
解析:如图,点E为格点,连接AE,BE,则易得,,易得,,,,,在中,,.故选A.
知识点3、 已知一边一锐角解直角三角形
一
边
一
角 一直角边
和一锐角 锐角、邻边
(如∠A,b) ∠B=90°-∠A,
,
锐角、对边
(如∠A,a) ∠B=90°-∠A,
,
斜边、锐角(如c,∠A) ∠B=90°-∠A,
,
【新知导学】
例3-11.在中,,,,求BC的长.
答案:4
解析:在中,,
,
,
.
例3-2.在中,,根据下列条件解直角三角形:
(1),;
(2),;
(3),.
答案:(1),,
(2),,
(3),,
解析:(1),,
.
,
,
.
(2),,
.
,
.
,
.
(3),,,
.
,
,
.
【对应导练】
1.如图是引拉线固定电线杆的示意图.已知:,,,则拉线的长是________m.
答案:6
解析:在直角中,,
则.
答:拉线AC的长是6.
2.如图,在中,是斜边上的高.若,则的值为( )
A. B. C. D.
答案:B
解析:∵是斜边上的高,
∴是直角三角形,.
∵在中,,
∴设,,
则,,
∴,
∵,
∴,
∴.
故选B.
二、题型训练
1.解直角三角形
1.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
答案:(1)见解析
(2)见解析
(3)见解析
解析:(1),
.
,.
,.
(2),.
,.
,.
(3),.
由,求出,
.
2.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
答案:
解析:方法一:将沿折叠后,点C恰好落在斜边的中点E处,
,,,
,,
.
又,
,
,
.
方法二:在中,,
设,则,
.
在中,,
即,
解得,
即.
故答案为:.
3.在中,,若,则( )
A. B. C. D.
答案:A
解析:根据题意可得:,
在中,,
,
故选:A.
2.解非直角三角形
4.如图,已知中,,,.求的面积.
答案:
解析:过点A作,垂足为点D,
在中,∵,
∴
∵,
∴
在中,∵,
∴,
∴
∴.
5.如图,在中,AD是BC边上的高,.
(1)求证:;
(2)若,,求的面积.
答案:(1)证明见解析
(2)的面积为48
解析:(1)是BC上的高
.
,.
在和中,
,,
又已知,
.
.
(2)在中,,故可设,.
.
,又,
,
由已知,.
.
.
6.在中,是BC边上的高,,则BC的长为_______.
答案:
解析:如图,
在中,AD是BC边上的高,,即,
在中,,
在 中,,,即,
根据勾股定理得:
故答案为:
3.构造直角三角形解决问题
7.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则_______.
答案:
解析:如图,取的中点D,连接,,
,,,
,
又点D是的中点,
,
,
故答案为:.
8.如图,在小山的东侧A点处有一个热气球,由于受风向的影响,该热气球以每分钟30米的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,求A,B两点间的距离.
答案:米
解析:如图,过点A作,垂足为D,
在中,
,(米),
(米).
在中,
,
(米).
9.如图,在矩形ABCD中,点E为矩形内一点,且,,,,则四边形ABCE的面积是_________.
答案:
解析:如图,连接AC,过点E分别作于点F,于点G,于点H,则四边形EFDH为矩形.在中,,,,,.又,平分.同理CE平分,点E是的内心,,,,,四边形EFDH是正方形,,,.
三、课堂达标
一、单选题(每小题4分,共32分)
1.如图,在中,已知,,则的长为( )
A. B. C. D.
答案:C
解析:∵在中,,,
∴;
故选C.
2.在中,,,,则的长为( )
A. B. C. D.
答案:C
解析:在中,,,,
,
.
故选:C.
3.在中,,若,则的值是( )
A. B. C. D.
答案:D
解析:由题意,得
,
,
,
故选:D.
4.如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米.
A. B. C. D.
答案:C
解析:在中,
∠A=35°,BC=50米,
sin35°=,
AB=(米).
故选:C.
5.在中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
答案:B
解析:根据题意作图如下:
由题意知:AB=m,∠A=,
,
,
即,
故选:B.
6.在中,,如果,,那么等于( )
A. B. C. D.
答案:B
解析:,
.
故选:B.
7.如图,斜坡的坡度,那么的值为( )
A.
B.
C.
D.
答案:C
解析:.
8.如图,直线l:分别与x轴、y轴交于点A、B.点P为直线l在第一象限的点.作的外接圆,延长交于点D,当的面积最小时,则的半径长为( )
A. B.2 C. D.3
答案:B
解析:当时,,
当时,,
解得:,
点,
,
,
,,
,
,
是直径,
,
,
,
,
当最小时,最小,此时,
,
即,
解得:,
,
,
.
故选:B.
二、填空题(每小题4分,共20分)
9.在中,已知,,,点M在边上,点N在边上,且,连接,当为等腰三角形时,______.
答案:5或或
解析:当时,如图1,
∵,
∴,
;
当时,如图2,作,则有,
,且,
,即,
解得:;
当时,如图3,作,则有,
,且,
,即,
解得:;
综上所述,答案为:5或或.
10.在中,是BC边上的高,,则BC的长为_______.
答案:
解析:如图,
在中,AD是BC边上的高,,即,
在中,,
在 中,,,即,
根据勾股定理得:
故答案为:
11.如图,在中,,,D为上一点,且满足,过D作交延长线于点E,则_________.
答案:
解析:如图,过点A作垂足为H,
,,
设,
,,
,,
,
,
,
解得,,
,,
,,
,
过点C作垂足为M,
,,
,,
,
,
故答案为:.
12.如图,在中,,,,将绕点A逆时针旋转得到,使点C落在边上,
(1)旋转角的度数是________.
(2)线段扫过部分的面积为_________;(结果保留)
答案:(1)
(2)
解析:(1),,
,
旋转角的度数,
故答案为:;
(2),,,
,
旋转角为,
,
线段所扫过部分的面积是.
故答案为:.
13.一副直角三角板如图放置,点C在的延长线上,,,,,,则________.
答案:
解析:过点B作于点M,
在中,,,,
,,
,
,
,
在中,,,
,
,
.
故答案是:.
三、解答题(每小题8分,共48分)
14.在中,,,,求BC的长.
答案:4
解析:在中,,
,
,
.
15.如图, 中, ,是的高, ,,求的长.
答案:∵,,,
∴,(角所对直角边等于斜边一半),
∴,(角所对直角边等于斜边一半).
解析:
16.如图,在中,,的周长为24,,点D为的中点.求、的长.
答案:的长为6,的长为4
解析:在中,,
,,
不妨设,,则.
又的周长为24,
,解得:,
的长为6,的长为8.
点D为的中点.
.
答:的长为6,的长为4.
17.阅读与思考.
请仔细阅读并完成相应的任务.
利用我们所学习的三角函数的相关知识可以解决许多关于三角形边长、角度、面积等问题.如图,在锐角中,,,的对边分别是a,b,c过点B作于点H,则,即,于是.在中,,在中,,,整理得.
任务:
(1)________,________;
(2)已知中,,,的对边分别是a,b,c,,,,求c.
答案:(1);
(2)
解析:(1)根据进行类比,
可得,,
故答案为:,.
(2),,,,
,
即,
解得,(舍去),
.
18.如图①,已知在中,,,,D是斜边AB的中点.
(1)求CD的长;
(2)如图②,过点D作AB的垂线交AC于点E,求DE的长;
(3)如图③,过点A作CD的垂线,垂足为M,求的值.
答案:(1)5
(2)
(3)
解析:(1),,
,,
D是AB的中点,.
(2)由(1)知,
在中,,.
(3),,
在中,,
设,,
则,,
,,
.
19.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
答案:(1)45°;9
(2)2
解析:(1)如图,作于E,设,
在中,,
,
,
,解得,
.
在中,,
,
为等腰直角三角形,
,
.
(2)为中线,
,
,
,
即的值为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
28.2 解直角三角形
学习目标:
1 理解直角三角形中除直角以外的五个元素之间的关系.
2 能综合运用勾股定理、直角三角形两个锐角互余及锐角三角函数解直角三角形.
老师告诉你
一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
直角三角形中(1)三边关系:a2+b2=c2(勾股定理)
(2)两锐角的关系:∠A+∠B=90°
(3)边角之间的关系:
,,,
,,.
一、知识点拨
知识点1、 解直角三角形
在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.
设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).
②锐角之间的关系:∠A+∠B=90°.
③边角之间的关系:
,,,
,,.
④,h为斜边上的高.
注意:(1)直角三角形中有一个元素为定值(直角为90°),是已知值.
(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).
(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.
【新知导学】
例1-1.如图,在中,,D为AB的中点,,则的值是( )
A. B.3 C. D.
例1-2.在中,,,,欲求的值,最适宜的做法是( )
A.计算的值求出 B.计算的值求出
C.计算的值求出 D.先根据求出,再利用求出
【对应导练】
1.如图,在中,,,.若点D在直线AB上(不与点A,B重合),且,则AD的长为__________.
2.在中,,.若是锐角三角形,则边长的取值范围是__________.
知识点2、 已知两边解直角三角形
已知条件 解法步骤
Rt△ABC
两
边 两直角边(a,b) 由求∠A,
∠B=90°-∠A,
斜边,一直角边(如c,a) 由求∠A,
∠B=90°-∠A,
【新知导学】
例2-1.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
例2-2.如图, 在中, ,,,AD是中线, BE平分 交AC 于点 E,于点F, 则 CF的长为__________.
【对应导练】
1.如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若,,则GF的长为( )
A. B. C. D.
2.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点处,AB,CD相交于点O,则的值为( )
A.2 B. C.3 D.
知识点3、 已知一边一锐角解直角三角形
一
边
一
角 一直角边
和一锐角 锐角、邻边
(如∠A,b) ∠B=90°-∠A,
,
锐角、对边
(如∠A,a) ∠B=90°-∠A,
,
斜边、锐角(如c,∠A) ∠B=90°-∠A,
,
【新知导学】
例3-11.在中,,,,求BC的长.
.
例3-2.在中,,根据下列条件解直角三角形:
(1),;
(2),;
(3),.
【对应导练】
1.如图是引拉线固定电线杆的示意图.已知:,,,则拉线的长是________m.
2.如图,在中,是斜边上的高.若,则的值为( )
A. B. C. D.
二、题型训练
1.解直角三角形
1.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
2.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
3.在中,,若,则( )
A. B. C. D.
2.解非直角三角形
4.如图,已知中,,,.求的面积.
5.如图,在中,AD是BC边上的高,.
(1)求证:;
(2)若,,求的面积.
6.在中,是BC边上的高,,则BC的长为_______.
3.构造直角三角形解决问题
7.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则_______.
8.如图,在小山的东侧A点处有一个热气球,由于受风向的影响,该热气球以每分钟30米的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,求A,B两点间的距离.
9.如图,在矩形ABCD中,点E为矩形内一点,且,,,,则四边形ABCE的面积是_________.
三、课堂达标
一、单选题(每小题4分,共32分)
1.如图,在中,已知,,则的长为( )
A. B. C. D.
2.在中,,,,则的长为( )
A. B. C. D.
3.在中,,若,则的值是( )
A. B. C. D.
4.如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米.
A. B. C. D.
5.在中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
6.在中,,如果,,那么等于( )
A. B. C. D.
7.如图,斜坡的坡度,那么的值为( )
A.
B.
C.
D.
8.如图,直线l:分别与x轴、y轴交于点A、B.点P为直线l在第一象限的点.作的外接圆,延长交于点D,当的面积最小时,则的半径长为( )
A. B.2 C. D.3
二、填空题(每小题4分,共20分)
9.在中,已知,,,点M在边上,点N在边上,且,连接,当为等腰三角形时,______.
10.在中,是BC边上的高,,则BC的长为_______.
11.如图,在中,,,D为上一点,且满足,过D作交延长线于点E,则_________.
12.如图,在中,,,,将绕点A逆时针旋转得到,使点C落在边上,
(1)旋转角的度数是________.
(2)线段扫过部分的面积为_________;(结果保留)
13.一副直角三角板如图放置,点C在的延长线上,,,,,,则________.
三、解答题(每小题8分,共48分)
14.在中,,,,求BC的长.
.
15.如图, 中, ,是的高, ,,求的长.
16.如图,在中,,的周长为24,,点D为的中点.求、的长.
17.阅读与思考.
请仔细阅读并完成相应的任务.
利用我们所学习的三角函数的相关知识可以解决许多关于三角形边长、角度、面积等问题.如图,在锐角中,,,的对边分别是a,b,c过点B作于点H,则,即,于是.在中,,在中,,,整理得.
任务:
(1)________,________;
(2)已知中,,,的对边分别是a,b,c,,,,求c.
18.如图①,已知在中,,,,D是斜边AB的中点.
(1)求CD的长;
(2)如图②,过点D作AB的垂线交AC于点E,求DE的长;
(3)如图③,过点A作CD的垂线,垂足为M,求的值.
19.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
28.2 解直角三角形
学习目标:
1 理解直角三角形中除直角以外的五个元素之间的关系.
2 能综合运用勾股定理、直角三角形两个锐角互余及锐角三角函数解直角三角形.
老师告诉你
一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
直角三角形中(1)三边关系:a2+b2=c2(勾股定理)
(2)两锐角的关系:∠A+∠B=90°
(3)边角之间的关系:
,,,
,,.
一、知识点拨
知识点1、 解直角三角形
在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.
设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).
②锐角之间的关系:∠A+∠B=90°.
③边角之间的关系:
,,,
,,.
④,h为斜边上的高.
注意:(1)直角三角形中有一个元素为定值(直角为90°),是已知值.
(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).
(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.
【新知导学】
例1-1.如图,在中,,D为AB的中点,,则的值是( )
A. B.3 C. D.
答案:B
解析:D为AB的中点,所以∠BCD=∠B = =
所以= =3
故选B
例1-2.在中,,,,欲求的值,最适宜的做法是( )
A.计算的值求出 B.计算的值求出
C.计算的值求出 D.先根据求出,再利用求出
答案:C
解析:根据“锐角三角函数”的定义可知,在中,当,,时,求、中的任何一个,都需要先求出BC的长;虽可直接由算出,但在求出后还需利用直角三角形中两锐角互余才能求出;而由:得到的值后就可直接求得的值了,所以C的方法更合适.
故选:C.
【对应导练】
1.如图,在中,,,.若点D在直线AB上(不与点A,B重合),且,则AD的长为__________.
答案:6或12
解析:在,,,,
当点D在点B左上方时,如图所示,
,
,
.
,
,
.
当点D在点B的右下方时,如图所示,
,,,
在中,,
,
综上所述,AD的长为6或12.故答案为:6或12.
2.在中,,.若是锐角三角形,则边长的取值范围是__________.
答案:
解析:如图,作的高,,
是锐角三角形,
,在的内部,
,,
在中,,,
,
,
又,
,
故答案为:.
知识点2、 已知两边解直角三角形
已知条件 解法步骤
Rt△ABC
两
边 两直角边(a,b) 由求∠A,
∠B=90°-∠A,
斜边,一直角边(如c,a) 由求∠A,
∠B=90°-∠A,
【新知导学】
例2-1.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
答案:
解析:方法一:将沿折叠后,点C恰好落在斜边的中点E处,
,,,
,,
.
又,
,
,
.
方法二:在中,,
设,则,
.
在中,,
即,
解得,
即.
故答案为:.
例2-2.如图, 在中, ,,,AD是中线, BE平分 交AC 于点 E,于点F, 则 CF的长为__________.
答案:
解析:在 中, ,,,. 如图,
过点E 作 于点G, 则,
,,
AD 是中线,,,,
,
,
【对应导练】
1.如图,正方形ABCD中,点E.F分别在边CD,AD上,BE与CF交于点G.若,,则GF的长为( )
A. B. C. D.
答案:A
解析:正方形ABCD中,,
,,
,
,
,
在和中,
,
,
,
,
,
,
故选:A.
2.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点处,AB,CD相交于点O,则的值为( )
A.2 B. C.3 D.
答案:A
解析:如图,点E为格点,连接AE,BE,则易得,,易得,,,,,在中,,.故选A.
知识点3、 已知一边一锐角解直角三角形
一
边
一
角 一直角边
和一锐角 锐角、邻边
(如∠A,b) ∠B=90°-∠A,
,
锐角、对边
(如∠A,a) ∠B=90°-∠A,
,
斜边、锐角(如c,∠A) ∠B=90°-∠A,
,
【新知导学】
例3-11.在中,,,,求BC的长.
答案:4
解析:在中,,
,
,
.
例3-2.在中,,根据下列条件解直角三角形:
(1),;
(2),;
(3),.
答案:(1),,
(2),,
(3),,
解析:(1),,
.
,
,
.
(2),,
.
,
.
,
.
(3),,,
.
,
,
.
【对应导练】
1.如图是引拉线固定电线杆的示意图.已知:,,,则拉线的长是________m.
答案:6
解析:在直角中,,
则.
答:拉线AC的长是6.
2.如图,在中,是斜边上的高.若,则的值为( )
A. B. C. D.
答案:B
解析:∵是斜边上的高,
∴是直角三角形,.
∵在中,,
∴设,,
则,,
∴,
∵,
∴,
∴.
故选B.
二、题型训练
1.解直角三角形
1.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
答案:(1)见解析
(2)见解析
(3)见解析
解析:(1),
.
,.
,.
(2),.
,.
,.
(3),.
由,求出,
.
2.如图,在中,,,D为上一点,将沿折叠后,点C恰好落在斜边的中点E处,则折痕的长为___.
答案:
解析:方法一:将沿折叠后,点C恰好落在斜边的中点E处,
,,,
,,
.
又,
,
,
.
方法二:在中,,
设,则,
.
在中,,
即,
解得,
即.
故答案为:.
3.在中,,若,则( )
A. B. C. D.
答案:A
解析:根据题意可得:,
在中,,
,
故选:A.
2.解非直角三角形
4.如图,已知中,,,.求的面积.
答案:
解析:过点A作,垂足为点D,
在中,∵,
∴
∵,
∴
在中,∵,
∴,
∴
∴.
5.如图,在中,AD是BC边上的高,.
(1)求证:;
(2)若,,求的面积.
答案:(1)证明见解析
(2)的面积为48
解析:(1)是BC上的高
.
,.
在和中,
,,
又已知,
.
.
(2)在中,,故可设,.
.
,又,
,
由已知,.
.
.
6.在中,是BC边上的高,,则BC的长为_______.
答案:
解析:如图,
在中,AD是BC边上的高,,即,
在中,,
在 中,,,即,
根据勾股定理得:
故答案为:
3.构造直角三角形解决问题
7.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则_______.
答案:
解析:如图,取的中点D,连接,,
,,,
,
又点D是的中点,
,
,
故答案为:.
8.如图,在小山的东侧A点处有一个热气球,由于受风向的影响,该热气球以每分钟30米的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,求A,B两点间的距离.
答案:米
解析:如图,过点A作,垂足为D,
在中,
,(米),
(米).
在中,
,
(米).
9.如图,在矩形ABCD中,点E为矩形内一点,且,,,,则四边形ABCE的面积是_________.
答案:
解析:如图,连接AC,过点E分别作于点F,于点G,于点H,则四边形EFDH为矩形.在中,,,,,.又,平分.同理CE平分,点E是的内心,,,,,四边形EFDH是正方形,,,.
三、课堂达标
一、单选题(每小题4分,共32分)
1.如图,在中,已知,,则的长为( )
A. B. C. D.
答案:C
解析:∵在中,,,
∴;
故选C.
2.在中,,,,则的长为( )
A. B. C. D.
答案:C
解析:在中,,,,
,
.
故选:C.
3.在中,,若,则的值是( )
A. B. C. D.
答案:D
解析:由题意,得
,
,
,
故选:D.
4.如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米.
A. B. C. D.
答案:C
解析:在中,
∠A=35°,BC=50米,
sin35°=,
AB=(米).
故选:C.
5.在中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
答案:B
解析:根据题意作图如下:
由题意知:AB=m,∠A=,
,
,
即,
故选:B.
6.在中,,如果,,那么等于( )
A. B. C. D.
答案:B
解析:,
.
故选:B.
7.如图,斜坡的坡度,那么的值为( )
A.
B.
C.
D.
答案:C
解析:.
8.如图,直线l:分别与x轴、y轴交于点A、B.点P为直线l在第一象限的点.作的外接圆,延长交于点D,当的面积最小时,则的半径长为( )
A. B.2 C. D.3
答案:B
解析:当时,,
当时,,
解得:,
点,
,
,
,,
,
,
是直径,
,
,
,
,
当最小时,最小,此时,
,
即,
解得:,
,
,
.
故选:B.
二、填空题(每小题4分,共20分)
9.在中,已知,,,点M在边上,点N在边上,且,连接,当为等腰三角形时,______.
答案:5或或
解析:当时,如图1,
∵,
∴,
;
当时,如图2,作,则有,
,且,
,即,
解得:;
当时,如图3,作,则有,
,且,
,即,
解得:;
综上所述,答案为:5或或.
10.在中,是BC边上的高,,则BC的长为_______.
答案:
解析:如图,
在中,AD是BC边上的高,,即,
在中,,
在 中,,,即,
根据勾股定理得:
故答案为:
11.如图,在中,,,D为上一点,且满足,过D作交延长线于点E,则_________.
答案:
解析:如图,过点A作垂足为H,
,,
设,
,,
,,
,
,
,
解得,,
,,
,,
,
过点C作垂足为M,
,,
,,
,
,
故答案为:.
12.如图,在中,,,,将绕点A逆时针旋转得到,使点C落在边上,
(1)旋转角的度数是________.
(2)线段扫过部分的面积为_________;(结果保留)
答案:(1)
(2)
解析:(1),,
,
旋转角的度数,
故答案为:;
(2),,,
,
旋转角为,
,
线段所扫过部分的面积是.
故答案为:.
13.一副直角三角板如图放置,点C在的延长线上,,,,,,则________.
答案:
解析:过点B作于点M,
在中,,,,
,,
,
,
,
在中,,,
,
,
.
故答案是:.
三、解答题(每小题8分,共48分)
14.在中,,,,求BC的长.
答案:4
解析:在中,,
,
,
.
15.如图, 中, ,是的高, ,,求的长.
答案:∵,,,
∴,(角所对直角边等于斜边一半),
∴,(角所对直角边等于斜边一半).
解析:
16.如图,在中,,的周长为24,,点D为的中点.求、的长.
答案:的长为6,的长为4
解析:在中,,
,,
不妨设,,则.
又的周长为24,
,解得:,
的长为6,的长为8.
点D为的中点.
.
答:的长为6,的长为4.
17.阅读与思考.
请仔细阅读并完成相应的任务.
利用我们所学习的三角函数的相关知识可以解决许多关于三角形边长、角度、面积等问题.如图,在锐角中,,,的对边分别是a,b,c过点B作于点H,则,即,于是.在中,,在中,,,整理得.
任务:
(1)________,________;
(2)已知中,,,的对边分别是a,b,c,,,,求c.
答案:(1);
(2)
解析:(1)根据进行类比,
可得,,
故答案为:,.
(2),,,,
,
即,
解得,(舍去),
.
18.如图①,已知在中,,,,D是斜边AB的中点.
(1)求CD的长;
(2)如图②,过点D作AB的垂线交AC于点E,求DE的长;
(3)如图③,过点A作CD的垂线,垂足为M,求的值.
答案:(1)5
(2)
(3)
解析:(1),,
,,
D是AB的中点,.
(2)由(1)知,
在中,,.
(3),,
在中,,
设,,
则,,
,,
.
19.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
答案:(1)45°;9
(2)2
解析:(1)如图,作于E,设,
在中,,
,
,
,解得,
.
在中,,
,
为等腰直角三角形,
,
.
(2)为中线,
,
,
,
即的值为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
