人教版九年级数学下名师点拨与训练第28章 锐角三角函数本章小结与复习(含解析)
文档属性
| 名称 | 人教版九年级数学下名师点拨与训练第28章 锐角三角函数本章小结与复习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 21:07:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
本章小结与复习
一、知识体系构建
知识点梳理
知识点1 锐角三角形
锐角三角函数:如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B)
定 义 表达式 取值范围 关 系
正弦 (∠A为锐角)
余弦 (∠A为锐角)
正切 (∠A为锐角)
注意
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数 30° 45° 60°
1
4. 正弦、余弦的增减性:当0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。
5 . 正切的增减性:当0°<<90°时,tan随的增大而增大,
知识点2 解直角三角形
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
直角三角形五元素之间的关系:
1. 勾股定理()
2. ∠A+∠B=90°
3. sin A= =
4. cos A= =
5. tan A= =
知识点3 解直角三角形解决实际问题
(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;
(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;
(3)选择合适的边角关系式,使运算简便、准确;
(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.
实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母i表示,即.
(3)坡角:坡面与水平面的夹角;
(4)坡度与坡角(用表示)的关系:i=tan.坡角越大,坡度越大,坡面越陡。
(5)方位角:指南或指北的方向线与目标方向线所成的小于90°角的为方位角.
高频考点
【考点1】求三角函数的值
【例1-1】如图,在平面直角坐标系中,点M的坐标为M(,2),那么cosα的值是( )
A. B. C. D.
【例1-2】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以为直径的圆经过点C,D,则的值为( )
A. B. C. D.
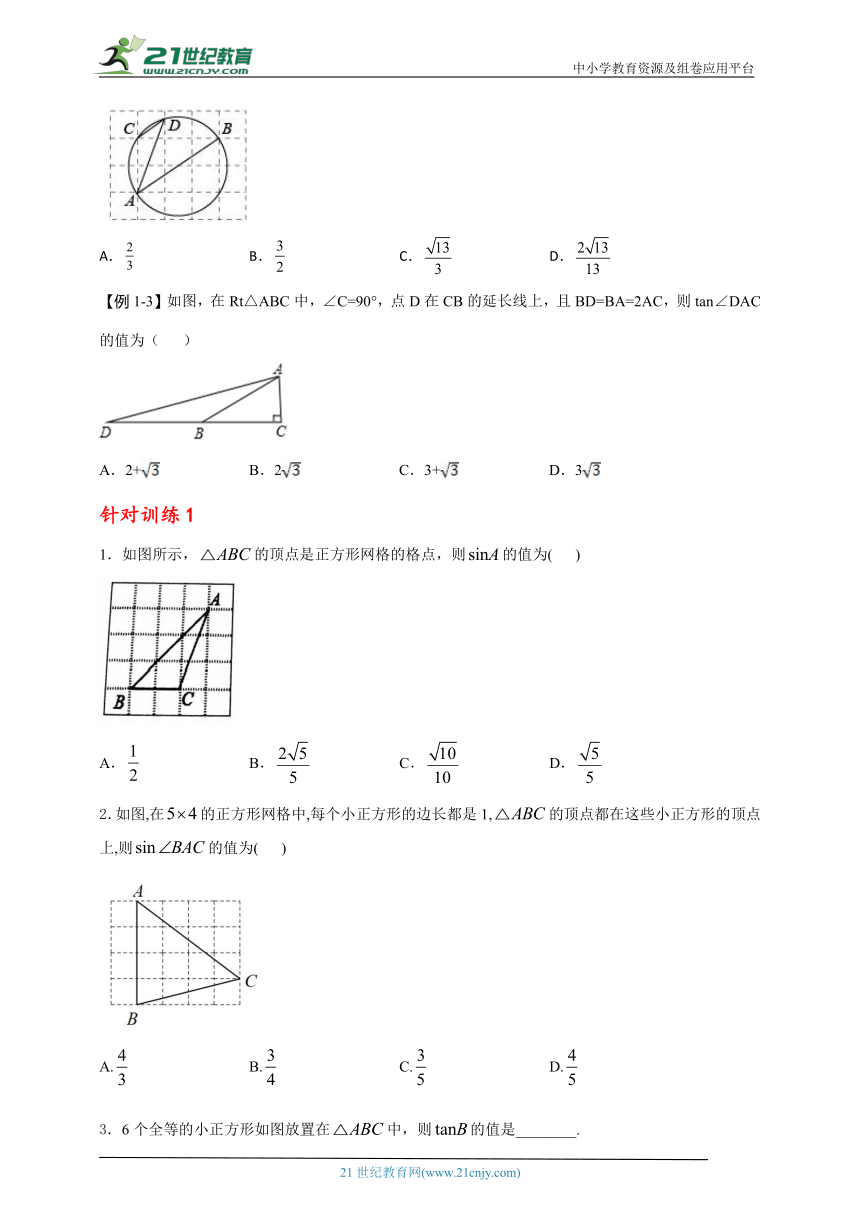
【例1-3】如图,在Rt△ABC中,∠C=90°,点D在CB的延长线上,且BD=BA=2AC,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
针对训练1
1.如图所示,的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
2.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
3.6个全等的小正方形如图放置在中,则的值是________.
4.如图,在的方格中,两条线段的夹角(锐角)为,则__________.
【考点2】特殊角的三角函数值
【例2-1】.已知为锐角,,则______.
【例2-2】.定义一种运算;,.例如:当,时,,则的值为________.
【例2-3】.在锐角中,若,则_________________.
针对训练2
1.在中,若,则∠C的度数是_________________
2.在中,,都是锐角,且,,则是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
4.计算:
(1);
(2).
5.综合与实践:在学习《解直角三角形》一章时,小邕同学对一个角的倍角的三角函数值与这个角的三角函数值是否有关系产生了浓厚的兴趣,并进行研究.
【初步尝试】我们知道:___________,___________.
发现:___________(填“=”或“”).
【实践探究】在解决“如图1,在中,,,,求的值”这一问题时,小邕想构造包含的直角三角形,延长到点D,使,连接BD,所以可得,问题即转化为求的正切值,请按小邕的思路求的值.
【拓展延伸】如图2,在中,,,.请模仿小邕的思路或者用你的新思路,试着求一求的值.
【考点3】解直角三角形
【例3-1】.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
【例3-2】.如图,在中,弦AB的长为8,点C在BO延长线上,且,.
(1)求的半径;
(2)求的正切值.
【例3-3】.如图, 在由边长为 1 的小正方形组成的网格中, 点A,B,C,D 都在这些小正方形的 顶点上, AB,CD相交于点O, 则
(1) AB与CD长度的大小关系是
(2)的值为
针对训练3
1.如图,是的中线,.
求:(1)的长;
(2)的值.
2.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
3.在中,分别是的对边,根据下列条件,解这个直角三角形.
(1);(2).
4.如图,在中,,,,求AC和AB的长.
5.已知a,b,c分别是中,,的对边,关于x的一元二次方程有两个相等的实数根,且.
(1)判断的形状;
(2)求的值.
【考点4】三角函数的应用
(1)视角问题
【例4-1】.某校数学兴趣小组学完“三角函数的应用”后,在校园内利用三角尺测量教学楼的高度,如图,小明同学站在点D处,将含角三角尺的一条直角边水平放置,此时三角尺的斜边刚好落在视线上(即此时的仰角是).沿教学楼向前走8米到达点F处,将含角三角尺的短直角边水平放置,此时三角尺的斜边也刚好落在视线上(即此时的仰角是).已知小明眼睛到地面的距离为1.6米,求教学楼的高度.(点D,F,B在同一水平线上,结果精确到0.1,参考数据:,)
针对训练4-1
1.交城县教育局为了丰富春节期间群众的文化生活,营造节日喜庆氛围,宣传教育新形象,特在卦山公园举办花灯展,并在公园的门口搭建了一座门楼(如图).某校“综合与实践”活动小组的同学们为了测量门楼的高度,设计了如下方案:
课题 测量门楼的高度
测量工具 无人机
测量示意图 说明:表示门楼,点A表示门楼的顶部,点B表示门楼的底部.点C,D为无人机两次测量的位置,米,点C,D在同一水平直线上,点A,B,C,D均在同一竖直平面内,与水平面垂直.
测量数据 从D处观测B处的俯角 从C处观测B处的俯角 从C处观测A处的俯角
…… ……
请你结合以上数据,帮助该小组的同学求出门楼的高度.(结果精确到米.参考数据:)
(2)方向角问题
【例4-2】.某中学组织学生到爱国主义教育基地进行红色研学活动,基地如图所示。学生从基地门口A处出发,先沿正北方向走500米到达B处的博物馆参观,再沿正东方向走到C处的科技馆体验,继续沿南偏东方向走到D处的党史纪念馆学习,最后回到基地门口A处集合返回。已知党史纪念馆D在基地门口A的北偏东方向600米处。求科技馆C与党史纪念馆D之间的距离(结果保留根号)。
针对训练4-2
2.人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.
(1)求B养殖场与灯塔C的距离(结果保留根号);
(2)甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据:,)
(3)坡度问题
【例4-3】.城市规划期间,欲拆除一电线杆,如图,已知距电线杆的水平距离的D处有一大坝,背水坡的坡度,坝高为,在坝顶点C处测得电线杆顶点A的仰角为,之间是宽为的行人道,试问在拆除电线杆时,为确保行人安全,是否需要将此人行道封上?(提示:在地面上,以点B为圆心,以为半径的圆形区域为危险区域)(参考数据:)
针对训练4-3
3.在学习解直角三角形以后,某班数学兴趣小组的同学测量了旗杆的高度,如图,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为6米,落在斜坡上的影长为4米,,点A、B、F三点共线,且,同一时刻,光线与旗杆的夹角为,斜坡的坡比为,
(1)求坡角的度数;
(2)旗杆的高度为多少米?(结果保留根号)
(4)其他问题
【例4-4】.图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管的长度为0.5米.则安装热水器的铁架水平横管BC的长度约为_____米.(结果精确到0.1米)参考数据:,,,,,
针对训练4-4
4.项目化学习
研究课题 如何设计遮阳篷
设计要求 遮阳篷既能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.
设计方案
如图:表示直角遮阳篷.遮阳篷水平部分垂直于墙面,表示窗户.
数据收集 通过查阅相关资料和实际测量:夏至日这一天的正午时刻太阳光线与遮阳篷的夹角最大,最大角;冬至日这一天的正午时刻,太阳光线与遮阳篷的夹角最小,最小角.
问题提出 (1)如图2,若墙面的高为米,要求设计的遮阳篷正好最大限度地遮住夏天炎热的阳光,求遮阳篷水平部分的长度.(2)如图3,当窗户时,设计的遮阳篷能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.求遮阳篷的长.(参考数据:,,,,,)
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
本章小结与复习
一、知识体系构建
知识点梳理
知识点1 锐角三角形
锐角三角函数:如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B)
定 义 表达式 取值范围 关 系
正弦 (∠A为锐角)
余弦 (∠A为锐角)
正切 (∠A为锐角)
注意
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数 30° 45° 60°
1
4. 正弦、余弦的增减性:当0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。
5 . 正切的增减性:当0°<<90°时,tan随的增大而增大,
知识点2 解直角三角形
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
直角三角形五元素之间的关系:
1. 勾股定理()
2. ∠A+∠B=90°
3. sin A= =
4. cos A= =
5. tan A= =
知识点3 解直角三角形解决实际问题
(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;
(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;
(3)选择合适的边角关系式,使运算简便、准确;
(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.
实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母i表示,即.
(3)坡角:坡面与水平面的夹角;
(4)坡度与坡角(用表示)的关系:i=tan.坡角越大,坡度越大,坡面越陡。
(5)方位角:指南或指北的方向线与目标方向线所成的小于90°角的为方位角.
高频考点
【考点1】求三角函数的值
【例1-1】如图,在平面直角坐标系中,点M的坐标为M(,2),那么cosα的值是( )
A. B. C. D.
【答案】D
【分析】
如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.
【详解】
解:如图,作MH⊥x轴于H.
∵M(,2),
∴OH=,MH=2,
∴OM==3,
∴cosα=,
故选:D.
【点睛】
本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【例1-2】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以为直径的圆经过点C,D,则的值为( )
A. B. C. D.
【答案】D
【分析】首先根据圆周角定理的推论可知,,然后在中,根据锐角三角函数的定义求出的正弦值.
【详解】解:如图,连接、.
和所对的弧长都是,
根据圆周角定理的推论知,.
在中,根据锐角三角函数的定义知,
,
,,
,
,
.
故选:D.
【点睛】本题考查了圆周角定理的推论,解直角三角形,勾股定理,锐角三角函数的定义,解答本题的关键是利用圆周角定理的推论把求的正弦值转化成求的正弦值,本题是一道比较不错的习题.
【例1-3】如图,在Rt△ABC中,∠C=90°,点D在CB的延长线上,且BD=BA=2AC,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
【答案】A
【详解】
在Rt△ABC中,BA=2AC,
∴∠ABC=30°,∠BAC=60°,
∵设BD=BA=2x,
∴AC=x,BC=x,
∴DC=DB+BC=2x+x,
则tan∠DAC=,
故选A.
针对训练1
1.如图所示,的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
答案:D
解析:在B点正上方找一点D,使,连接CD交AB于点O,由网格可得: ,则,
故.故选D
2.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
答案:D
解析:如图,过C作于D,则,
.
.
故选D.
3.6个全等的小正方形如图放置在中,则的值是________.
答案:
解析:如图,
有6个大小相同的小正方形,恰好如图放置在中,设小正方形的边长为a,
,,,
,
,
.
故答案为:.
4.如图,在的方格中,两条线段的夹角(锐角)为,则__________.
答案:
解析:如图添加字母,过A作,使,
,
连结BC,
在中,
,
,,
.
,,
,
,
故答案为:.
【考点2】特殊角的三角函数值
【例2-1】.已知为锐角,,则______.
答案:
解析:∵a为锐角,且,
∴,
解得:.
故答案为:.
【例2-2】.定义一种运算;,.例如:当,时,,则的值为________.
答案:
解析:
.
故答案为:.
【例2-3】.在锐角中,若,则_________________.
答案:
解析:,,
,
,,
(负值舍去),,
,
,
,
故答案为:.
针对训练2
1.在中,若,则∠C的度数是_________________
答案:/度
解析:,,
,,
,,
,,
;
故答案为:.
2.在中,,都是锐角,且,,则是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
答案:B
解析:∵中,、都是锐角,,,
∴.
∴.
故选B.
3.计算:.
答案:3
解析:原式
.
4.计算:
(1);
(2).
答案:(1)
(2)
解析:(1)原式
;
(2)原式
.
5.综合与实践:在学习《解直角三角形》一章时,小邕同学对一个角的倍角的三角函数值与这个角的三角函数值是否有关系产生了浓厚的兴趣,并进行研究.
【初步尝试】我们知道:___________,___________.
发现:___________(填“=”或“”).
【实践探究】在解决“如图1,在中,,,,求的值”这一问题时,小邕想构造包含的直角三角形,延长到点D,使,连接BD,所以可得,问题即转化为求的正切值,请按小邕的思路求的值.
【拓展延伸】如图2,在中,,,.请模仿小邕的思路或者用你的新思路,试着求一求的值.
答案:【初步尝试】,,
【实践探究】
【拓展延伸】
解析:【初步尝试】,,,
故答案为:,,;
【实践探究】如图1,在中,,,,
.
,
,
,,
.
【拓展延伸】如图2,作的垂直平分线交于点E,连接.
则,,.
中,,,.
,.
设,则,
在中,,
解得,即,.
.
【考点3】解直角三角形
【例3-1】.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
答案:(1)见解析
(2)见解析
(3)见解析
解析:(1),
.
,.
,.
(2),.
,.
,.
(3),.
由,求出,
.
【例3-2】.如图,在中,弦AB的长为8,点C在BO延长线上,且,.
(1)求的半径;
(2)求的正切值.
答案:(1)5
解析:如图,过点O作,垂足为D.
,.
在中,,
.
的半径为5.
(2)答案:
解析:如图,过点C作,垂足为E.
,,
.
,,
.
,即,
..
在中,.
在中,.
的正切值为.
【例3-3】.如图, 在由边长为 1 的小正方形组成的网格中, 点A,B,C,D 都在这些小正方形的 顶点上, AB,CD相交于点O, 则
(1) AB与CD长度的大小关系是
(2)的值为
答案:(1)
(2)2
解析:(1)由勾股定理得,,.
(2)如图, 取格点E, 连接AE, 则.
连接BE, 可得,
.
针对训练3
1.如图,是的中线,.
求:(1)的长;
(2)的值.
答案:(1)4
(2)
解析:(1)如图,过,点A作于点E.
.
在中,,
.
在中,,
.
.
(2)是的中线,.
.
又°.
.
2.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
答案:(1)45°;9
(2)2
解析:(1)如图,作于E,设,
在中,,
,
,
,解得,
.
在中,,
,
为等腰直角三角形,
,
.
(2)为中线,
,
,
,
即的值为2.
3.在中,分别是的对边,根据下列条件,解这个直角三角形.
(1);(2).
答案:(1)8
(2)2
解析:(1),
由,知.
由,知.
(2)由,得,
.
,
.
4.如图,在中,,,,求AC和AB的长.
答案:,
解析:如图,过点C作于点D.
在中,,,
,.
在中,,,
.
,.
5.已知a,b,c分别是中,,的对边,关于x的一元二次方程有两个相等的实数根,且.
(1)判断的形状;
(2)求的值.
答案:(1)为直角三角形
(2)
解析:(1)将方程整理,得,
则.
方程有两个相等的实数根,
,
即.
为直角三角形,且.
(2)由,得.①
将①代入,得.
,
即.
由①可知,,
.
.②
将②代入①,得.
在中,.
【考点4】三角函数的应用
(1)视角问题
【例4-1】.某校数学兴趣小组学完“三角函数的应用”后,在校园内利用三角尺测量教学楼的高度,如图,小明同学站在点D处,将含角三角尺的一条直角边水平放置,此时三角尺的斜边刚好落在视线上(即此时的仰角是).沿教学楼向前走8米到达点F处,将含角三角尺的短直角边水平放置,此时三角尺的斜边也刚好落在视线上(即此时的仰角是).已知小明眼睛到地面的距离为1.6米,求教学楼的高度.(点D,F,B在同一水平线上,结果精确到0.1,参考数据:,)
答案:教学楼的高约为20.5米
解析:如图,连接并延长,交于点M,设米.
由题意可知,四边形,四边形是矩形,,
,,
在中,,
.
在中,,,
解得,
(米)
答:教学楼的高约为20.5米.
针对训练4-1
1.交城县教育局为了丰富春节期间群众的文化生活,营造节日喜庆氛围,宣传教育新形象,特在卦山公园举办花灯展,并在公园的门口搭建了一座门楼(如图).某校“综合与实践”活动小组的同学们为了测量门楼的高度,设计了如下方案:
课题 测量门楼的高度
测量工具 无人机
测量示意图 说明:表示门楼,点A表示门楼的顶部,点B表示门楼的底部.点C,D为无人机两次测量的位置,米,点C,D在同一水平直线上,点A,B,C,D均在同一竖直平面内,与水平面垂直.
测量数据 从D处观测B处的俯角 从C处观测B处的俯角 从C处观测A处的俯角
…… ……
请你结合以上数据,帮助该小组的同学求出门楼的高度.(结果精确到米.参考数据:)
答案:米
解析:如下图,延长,交于点E,
由题意可知,,,,
在中,,
∴,
∴,
设米,则米,
∵米,
∴米,
在中,可有,
∴,
∴,
∴,
在中,
∵,,
∴,
∴,
∴,即,
解得,
∴米.
(2)方向角问题
【例4-2】.某中学组织学生到爱国主义教育基地进行红色研学活动,基地如图所示。学生从基地门口A处出发,先沿正北方向走500米到达B处的博物馆参观,再沿正东方向走到C处的科技馆体验,继续沿南偏东方向走到D处的党史纪念馆学习,最后回到基地门口A处集合返回。已知党史纪念馆D在基地门口A的北偏东方向600米处。求科技馆C与党史纪念馆D之间的距离(结果保留根号)。
答案:
解析:如答案图1,过点D作,垂足为E,过点C作,垂足为F,
。
根据题意得,,
。
在中,
,
.
.
.
四边形BEFC是矩形,.
在中,
.
答:科技馆C与党史纪念馆D之间的距离为米。
针对训练4-2
2.人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.
(1)求B养殖场与灯塔C的距离(结果保留根号);
(2)甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据:,)
答案:(1)米
(2)甲组能在9分钟内到达B处
解析:(1)如图,过点C作于点D,
根据题意得:,,
∴,,
∴米,
∴米,
即B养殖场与灯塔C的距离为米;
(2)米,
∴米,
∴甲组到达B处所需时间为分钟分钟,
∴甲组能在9分钟内到达B处.
(3)坡度问题
【例4-3】.城市规划期间,欲拆除一电线杆,如图,已知距电线杆的水平距离的D处有一大坝,背水坡的坡度,坝高为,在坝顶点C处测得电线杆顶点A的仰角为,之间是宽为的行人道,试问在拆除电线杆时,为确保行人安全,是否需要将此人行道封上?(提示:在地面上,以点B为圆心,以为半径的圆形区域为危险区域)(参考数据:)
答案:不需封闭人行道,理由见解析
解析:如图,作于点M,
由题易知为矩形.
,,
背水坡的坡度,
,
.
.
在中,
,
.
.
而.
.故不需封闭人行道.
针对训练4-3
3.在学习解直角三角形以后,某班数学兴趣小组的同学测量了旗杆的高度,如图,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为6米,落在斜坡上的影长为4米,,点A、B、F三点共线,且,同一时刻,光线与旗杆的夹角为,斜坡的坡比为,
(1)求坡角的度数;
(2)旗杆的高度为多少米?(结果保留根号)
答案:(1)
(2)(米)
解析:(1)如图,
过C作于M,过D作交于N,交与O,
,,
,
为矩形,
的坡比为,
,
,
,
;
(2)由(1)可知,
,
在中,,(米),
(米),
(米),
(米),
(米),
在中,,
,
(米),
(米).
(4)其他问题
【例4-4】.图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管的长度为0.5米.则安装热水器的铁架水平横管BC的长度约为_____米.(结果精确到0.1米)参考数据:,,,,,
答案:米
解析:如图,过B作交于点F.
在中,,
则(米).
在中,,
则(米).
由题意得,四边形是矩形.
(米),(米),
(米),
在中,,
则(米),
(米),
答:安装热水器的铁架竖直管的长度约为米.
故答案为:.
针对训练4-4
4.项目化学习
研究课题 如何设计遮阳篷
设计要求 遮阳篷既能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.
设计方案
如图:表示直角遮阳篷.遮阳篷水平部分垂直于墙面,表示窗户.
数据收集 通过查阅相关资料和实际测量:夏至日这一天的正午时刻太阳光线与遮阳篷的夹角最大,最大角;冬至日这一天的正午时刻,太阳光线与遮阳篷的夹角最小,最小角.
问题提出 (1)如图2,若墙面的高为米,要求设计的遮阳篷正好最大限度地遮住夏天炎热的阳光,求遮阳篷水平部分的长度.(2)如图3,当窗户时,设计的遮阳篷能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.求遮阳篷的长.(参考数据:,,,,,)
答案:(1)
(2)
解析:(1)如图1,在中,∵,,
∴,
∴,
∴的长为;
(2)如图2,在中,∵,
∴,
∴,
在中,∵,
∴,
∴,
∴,
∴,
∴遮阳篷的长为.
对边
邻边
斜边
A
C
B
对边
邻边
斜边
A
C
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
本章小结与复习
一、知识体系构建
知识点梳理
知识点1 锐角三角形
锐角三角函数:如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B)
定 义 表达式 取值范围 关 系
正弦 (∠A为锐角)
余弦 (∠A为锐角)
正切 (∠A为锐角)
注意
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数 30° 45° 60°
1
4. 正弦、余弦的增减性:当0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。
5 . 正切的增减性:当0°<<90°时,tan随的增大而增大,
知识点2 解直角三角形
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
直角三角形五元素之间的关系:
1. 勾股定理()
2. ∠A+∠B=90°
3. sin A= =
4. cos A= =
5. tan A= =
知识点3 解直角三角形解决实际问题
(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;
(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;
(3)选择合适的边角关系式,使运算简便、准确;
(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.
实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母i表示,即.
(3)坡角:坡面与水平面的夹角;
(4)坡度与坡角(用表示)的关系:i=tan.坡角越大,坡度越大,坡面越陡。
(5)方位角:指南或指北的方向线与目标方向线所成的小于90°角的为方位角.
高频考点
【考点1】求三角函数的值
【例1-1】如图,在平面直角坐标系中,点M的坐标为M(,2),那么cosα的值是( )
A. B. C. D.
【例1-2】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以为直径的圆经过点C,D,则的值为( )
A. B. C. D.
【例1-3】如图,在Rt△ABC中,∠C=90°,点D在CB的延长线上,且BD=BA=2AC,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
针对训练1
1.如图所示,的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
2.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
3.6个全等的小正方形如图放置在中,则的值是________.
4.如图,在的方格中,两条线段的夹角(锐角)为,则__________.
【考点2】特殊角的三角函数值
【例2-1】.已知为锐角,,则______.
【例2-2】.定义一种运算;,.例如:当,时,,则的值为________.
【例2-3】.在锐角中,若,则_________________.
针对训练2
1.在中,若,则∠C的度数是_________________
2.在中,,都是锐角,且,,则是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
4.计算:
(1);
(2).
5.综合与实践:在学习《解直角三角形》一章时,小邕同学对一个角的倍角的三角函数值与这个角的三角函数值是否有关系产生了浓厚的兴趣,并进行研究.
【初步尝试】我们知道:___________,___________.
发现:___________(填“=”或“”).
【实践探究】在解决“如图1,在中,,,,求的值”这一问题时,小邕想构造包含的直角三角形,延长到点D,使,连接BD,所以可得,问题即转化为求的正切值,请按小邕的思路求的值.
【拓展延伸】如图2,在中,,,.请模仿小邕的思路或者用你的新思路,试着求一求的值.
【考点3】解直角三角形
【例3-1】.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
【例3-2】.如图,在中,弦AB的长为8,点C在BO延长线上,且,.
(1)求的半径;
(2)求的正切值.
【例3-3】.如图, 在由边长为 1 的小正方形组成的网格中, 点A,B,C,D 都在这些小正方形的 顶点上, AB,CD相交于点O, 则
(1) AB与CD长度的大小关系是
(2)的值为
针对训练3
1.如图,是的中线,.
求:(1)的长;
(2)的值.
2.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
3.在中,分别是的对边,根据下列条件,解这个直角三角形.
(1);(2).
4.如图,在中,,,,求AC和AB的长.
5.已知a,b,c分别是中,,的对边,关于x的一元二次方程有两个相等的实数根,且.
(1)判断的形状;
(2)求的值.
【考点4】三角函数的应用
(1)视角问题
【例4-1】.某校数学兴趣小组学完“三角函数的应用”后,在校园内利用三角尺测量教学楼的高度,如图,小明同学站在点D处,将含角三角尺的一条直角边水平放置,此时三角尺的斜边刚好落在视线上(即此时的仰角是).沿教学楼向前走8米到达点F处,将含角三角尺的短直角边水平放置,此时三角尺的斜边也刚好落在视线上(即此时的仰角是).已知小明眼睛到地面的距离为1.6米,求教学楼的高度.(点D,F,B在同一水平线上,结果精确到0.1,参考数据:,)
针对训练4-1
1.交城县教育局为了丰富春节期间群众的文化生活,营造节日喜庆氛围,宣传教育新形象,特在卦山公园举办花灯展,并在公园的门口搭建了一座门楼(如图).某校“综合与实践”活动小组的同学们为了测量门楼的高度,设计了如下方案:
课题 测量门楼的高度
测量工具 无人机
测量示意图 说明:表示门楼,点A表示门楼的顶部,点B表示门楼的底部.点C,D为无人机两次测量的位置,米,点C,D在同一水平直线上,点A,B,C,D均在同一竖直平面内,与水平面垂直.
测量数据 从D处观测B处的俯角 从C处观测B处的俯角 从C处观测A处的俯角
…… ……
请你结合以上数据,帮助该小组的同学求出门楼的高度.(结果精确到米.参考数据:)
(2)方向角问题
【例4-2】.某中学组织学生到爱国主义教育基地进行红色研学活动,基地如图所示。学生从基地门口A处出发,先沿正北方向走500米到达B处的博物馆参观,再沿正东方向走到C处的科技馆体验,继续沿南偏东方向走到D处的党史纪念馆学习,最后回到基地门口A处集合返回。已知党史纪念馆D在基地门口A的北偏东方向600米处。求科技馆C与党史纪念馆D之间的距离(结果保留根号)。
针对训练4-2
2.人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.
(1)求B养殖场与灯塔C的距离(结果保留根号);
(2)甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据:,)
(3)坡度问题
【例4-3】.城市规划期间,欲拆除一电线杆,如图,已知距电线杆的水平距离的D处有一大坝,背水坡的坡度,坝高为,在坝顶点C处测得电线杆顶点A的仰角为,之间是宽为的行人道,试问在拆除电线杆时,为确保行人安全,是否需要将此人行道封上?(提示:在地面上,以点B为圆心,以为半径的圆形区域为危险区域)(参考数据:)
针对训练4-3
3.在学习解直角三角形以后,某班数学兴趣小组的同学测量了旗杆的高度,如图,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为6米,落在斜坡上的影长为4米,,点A、B、F三点共线,且,同一时刻,光线与旗杆的夹角为,斜坡的坡比为,
(1)求坡角的度数;
(2)旗杆的高度为多少米?(结果保留根号)
(4)其他问题
【例4-4】.图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管的长度为0.5米.则安装热水器的铁架水平横管BC的长度约为_____米.(结果精确到0.1米)参考数据:,,,,,
针对训练4-4
4.项目化学习
研究课题 如何设计遮阳篷
设计要求 遮阳篷既能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.
设计方案
如图:表示直角遮阳篷.遮阳篷水平部分垂直于墙面,表示窗户.
数据收集 通过查阅相关资料和实际测量:夏至日这一天的正午时刻太阳光线与遮阳篷的夹角最大,最大角;冬至日这一天的正午时刻,太阳光线与遮阳篷的夹角最小,最小角.
问题提出 (1)如图2,若墙面的高为米,要求设计的遮阳篷正好最大限度地遮住夏天炎热的阳光,求遮阳篷水平部分的长度.(2)如图3,当窗户时,设计的遮阳篷能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.求遮阳篷的长.(参考数据:,,,,,)
人教版九年级数学下名师点拨与训练
第28章 锐角三角函数
本章小结与复习
一、知识体系构建
知识点梳理
知识点1 锐角三角形
锐角三角函数:如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B)
定 义 表达式 取值范围 关 系
正弦 (∠A为锐角)
余弦 (∠A为锐角)
正切 (∠A为锐角)
注意
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数 30° 45° 60°
1
4. 正弦、余弦的增减性:当0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。
5 . 正切的增减性:当0°<<90°时,tan随的增大而增大,
知识点2 解直角三角形
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
直角三角形五元素之间的关系:
1. 勾股定理()
2. ∠A+∠B=90°
3. sin A= =
4. cos A= =
5. tan A= =
知识点3 解直角三角形解决实际问题
(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;
(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;
(3)选择合适的边角关系式,使运算简便、准确;
(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.
实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母i表示,即.
(3)坡角:坡面与水平面的夹角;
(4)坡度与坡角(用表示)的关系:i=tan.坡角越大,坡度越大,坡面越陡。
(5)方位角:指南或指北的方向线与目标方向线所成的小于90°角的为方位角.
高频考点
【考点1】求三角函数的值
【例1-1】如图,在平面直角坐标系中,点M的坐标为M(,2),那么cosα的值是( )
A. B. C. D.
【答案】D
【分析】
如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.
【详解】
解:如图,作MH⊥x轴于H.
∵M(,2),
∴OH=,MH=2,
∴OM==3,
∴cosα=,
故选:D.
【点睛】
本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【例1-2】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以为直径的圆经过点C,D,则的值为( )
A. B. C. D.
【答案】D
【分析】首先根据圆周角定理的推论可知,,然后在中,根据锐角三角函数的定义求出的正弦值.
【详解】解:如图,连接、.
和所对的弧长都是,
根据圆周角定理的推论知,.
在中,根据锐角三角函数的定义知,
,
,,
,
,
.
故选:D.
【点睛】本题考查了圆周角定理的推论,解直角三角形,勾股定理,锐角三角函数的定义,解答本题的关键是利用圆周角定理的推论把求的正弦值转化成求的正弦值,本题是一道比较不错的习题.
【例1-3】如图,在Rt△ABC中,∠C=90°,点D在CB的延长线上,且BD=BA=2AC,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
【答案】A
【详解】
在Rt△ABC中,BA=2AC,
∴∠ABC=30°,∠BAC=60°,
∵设BD=BA=2x,
∴AC=x,BC=x,
∴DC=DB+BC=2x+x,
则tan∠DAC=,
故选A.
针对训练1
1.如图所示,的顶点是正方形网格的格点,则的值为( )
A. B. C. D.
答案:D
解析:在B点正上方找一点D,使,连接CD交AB于点O,由网格可得: ,则,
故.故选D
2.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
答案:D
解析:如图,过C作于D,则,
.
.
故选D.
3.6个全等的小正方形如图放置在中,则的值是________.
答案:
解析:如图,
有6个大小相同的小正方形,恰好如图放置在中,设小正方形的边长为a,
,,,
,
,
.
故答案为:.
4.如图,在的方格中,两条线段的夹角(锐角)为,则__________.
答案:
解析:如图添加字母,过A作,使,
,
连结BC,
在中,
,
,,
.
,,
,
,
故答案为:.
【考点2】特殊角的三角函数值
【例2-1】.已知为锐角,,则______.
答案:
解析:∵a为锐角,且,
∴,
解得:.
故答案为:.
【例2-2】.定义一种运算;,.例如:当,时,,则的值为________.
答案:
解析:
.
故答案为:.
【例2-3】.在锐角中,若,则_________________.
答案:
解析:,,
,
,,
(负值舍去),,
,
,
,
故答案为:.
针对训练2
1.在中,若,则∠C的度数是_________________
答案:/度
解析:,,
,,
,,
,,
;
故答案为:.
2.在中,,都是锐角,且,,则是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
答案:B
解析:∵中,、都是锐角,,,
∴.
∴.
故选B.
3.计算:.
答案:3
解析:原式
.
4.计算:
(1);
(2).
答案:(1)
(2)
解析:(1)原式
;
(2)原式
.
5.综合与实践:在学习《解直角三角形》一章时,小邕同学对一个角的倍角的三角函数值与这个角的三角函数值是否有关系产生了浓厚的兴趣,并进行研究.
【初步尝试】我们知道:___________,___________.
发现:___________(填“=”或“”).
【实践探究】在解决“如图1,在中,,,,求的值”这一问题时,小邕想构造包含的直角三角形,延长到点D,使,连接BD,所以可得,问题即转化为求的正切值,请按小邕的思路求的值.
【拓展延伸】如图2,在中,,,.请模仿小邕的思路或者用你的新思路,试着求一求的值.
答案:【初步尝试】,,
【实践探究】
【拓展延伸】
解析:【初步尝试】,,,
故答案为:,,;
【实践探究】如图1,在中,,,,
.
,
,
,,
.
【拓展延伸】如图2,作的垂直平分线交于点E,连接.
则,,.
中,,,.
,.
设,则,
在中,,
解得,即,.
.
【考点3】解直角三角形
【例3-1】.在中,.
(1)已知,c,写出解的过程;
(2)已知,a,写出解的过程;
(3)已知a,c,写出解的过程.
答案:(1)见解析
(2)见解析
(3)见解析
解析:(1),
.
,.
,.
(2),.
,.
,.
(3),.
由,求出,
.
【例3-2】.如图,在中,弦AB的长为8,点C在BO延长线上,且,.
(1)求的半径;
(2)求的正切值.
答案:(1)5
解析:如图,过点O作,垂足为D.
,.
在中,,
.
的半径为5.
(2)答案:
解析:如图,过点C作,垂足为E.
,,
.
,,
.
,即,
..
在中,.
在中,.
的正切值为.
【例3-3】.如图, 在由边长为 1 的小正方形组成的网格中, 点A,B,C,D 都在这些小正方形的 顶点上, AB,CD相交于点O, 则
(1) AB与CD长度的大小关系是
(2)的值为
答案:(1)
(2)2
解析:(1)由勾股定理得,,.
(2)如图, 取格点E, 连接AE, 则.
连接BE, 可得,
.
针对训练3
1.如图,是的中线,.
求:(1)的长;
(2)的值.
答案:(1)4
(2)
解析:(1)如图,过,点A作于点E.
.
在中,,
.
在中,,
.
.
(2)是的中线,.
.
又°.
.
2.如图,在中,是边上的中线,是锐角,且.
(1)求的度数与的值;
(2)求的值.
答案:(1)45°;9
(2)2
解析:(1)如图,作于E,设,
在中,,
,
,
,解得,
.
在中,,
,
为等腰直角三角形,
,
.
(2)为中线,
,
,
,
即的值为2.
3.在中,分别是的对边,根据下列条件,解这个直角三角形.
(1);(2).
答案:(1)8
(2)2
解析:(1),
由,知.
由,知.
(2)由,得,
.
,
.
4.如图,在中,,,,求AC和AB的长.
答案:,
解析:如图,过点C作于点D.
在中,,,
,.
在中,,,
.
,.
5.已知a,b,c分别是中,,的对边,关于x的一元二次方程有两个相等的实数根,且.
(1)判断的形状;
(2)求的值.
答案:(1)为直角三角形
(2)
解析:(1)将方程整理,得,
则.
方程有两个相等的实数根,
,
即.
为直角三角形,且.
(2)由,得.①
将①代入,得.
,
即.
由①可知,,
.
.②
将②代入①,得.
在中,.
【考点4】三角函数的应用
(1)视角问题
【例4-1】.某校数学兴趣小组学完“三角函数的应用”后,在校园内利用三角尺测量教学楼的高度,如图,小明同学站在点D处,将含角三角尺的一条直角边水平放置,此时三角尺的斜边刚好落在视线上(即此时的仰角是).沿教学楼向前走8米到达点F处,将含角三角尺的短直角边水平放置,此时三角尺的斜边也刚好落在视线上(即此时的仰角是).已知小明眼睛到地面的距离为1.6米,求教学楼的高度.(点D,F,B在同一水平线上,结果精确到0.1,参考数据:,)
答案:教学楼的高约为20.5米
解析:如图,连接并延长,交于点M,设米.
由题意可知,四边形,四边形是矩形,,
,,
在中,,
.
在中,,,
解得,
(米)
答:教学楼的高约为20.5米.
针对训练4-1
1.交城县教育局为了丰富春节期间群众的文化生活,营造节日喜庆氛围,宣传教育新形象,特在卦山公园举办花灯展,并在公园的门口搭建了一座门楼(如图).某校“综合与实践”活动小组的同学们为了测量门楼的高度,设计了如下方案:
课题 测量门楼的高度
测量工具 无人机
测量示意图 说明:表示门楼,点A表示门楼的顶部,点B表示门楼的底部.点C,D为无人机两次测量的位置,米,点C,D在同一水平直线上,点A,B,C,D均在同一竖直平面内,与水平面垂直.
测量数据 从D处观测B处的俯角 从C处观测B处的俯角 从C处观测A处的俯角
…… ……
请你结合以上数据,帮助该小组的同学求出门楼的高度.(结果精确到米.参考数据:)
答案:米
解析:如下图,延长,交于点E,
由题意可知,,,,
在中,,
∴,
∴,
设米,则米,
∵米,
∴米,
在中,可有,
∴,
∴,
∴,
在中,
∵,,
∴,
∴,
∴,即,
解得,
∴米.
(2)方向角问题
【例4-2】.某中学组织学生到爱国主义教育基地进行红色研学活动,基地如图所示。学生从基地门口A处出发,先沿正北方向走500米到达B处的博物馆参观,再沿正东方向走到C处的科技馆体验,继续沿南偏东方向走到D处的党史纪念馆学习,最后回到基地门口A处集合返回。已知党史纪念馆D在基地门口A的北偏东方向600米处。求科技馆C与党史纪念馆D之间的距离(结果保留根号)。
答案:
解析:如答案图1,过点D作,垂足为E,过点C作,垂足为F,
。
根据题意得,,
。
在中,
,
.
.
.
四边形BEFC是矩形,.
在中,
.
答:科技馆C与党史纪念馆D之间的距离为米。
针对训练4-2
2.人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.
(1)求B养殖场与灯塔C的距离(结果保留根号);
(2)甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据:,)
答案:(1)米
(2)甲组能在9分钟内到达B处
解析:(1)如图,过点C作于点D,
根据题意得:,,
∴,,
∴米,
∴米,
即B养殖场与灯塔C的距离为米;
(2)米,
∴米,
∴甲组到达B处所需时间为分钟分钟,
∴甲组能在9分钟内到达B处.
(3)坡度问题
【例4-3】.城市规划期间,欲拆除一电线杆,如图,已知距电线杆的水平距离的D处有一大坝,背水坡的坡度,坝高为,在坝顶点C处测得电线杆顶点A的仰角为,之间是宽为的行人道,试问在拆除电线杆时,为确保行人安全,是否需要将此人行道封上?(提示:在地面上,以点B为圆心,以为半径的圆形区域为危险区域)(参考数据:)
答案:不需封闭人行道,理由见解析
解析:如图,作于点M,
由题易知为矩形.
,,
背水坡的坡度,
,
.
.
在中,
,
.
.
而.
.故不需封闭人行道.
针对训练4-3
3.在学习解直角三角形以后,某班数学兴趣小组的同学测量了旗杆的高度,如图,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为6米,落在斜坡上的影长为4米,,点A、B、F三点共线,且,同一时刻,光线与旗杆的夹角为,斜坡的坡比为,
(1)求坡角的度数;
(2)旗杆的高度为多少米?(结果保留根号)
答案:(1)
(2)(米)
解析:(1)如图,
过C作于M,过D作交于N,交与O,
,,
,
为矩形,
的坡比为,
,
,
,
;
(2)由(1)可知,
,
在中,,(米),
(米),
(米),
(米),
(米),
在中,,
,
(米),
(米).
(4)其他问题
【例4-4】.图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管的长度为0.5米.则安装热水器的铁架水平横管BC的长度约为_____米.(结果精确到0.1米)参考数据:,,,,,
答案:米
解析:如图,过B作交于点F.
在中,,
则(米).
在中,,
则(米).
由题意得,四边形是矩形.
(米),(米),
(米),
在中,,
则(米),
(米),
答:安装热水器的铁架竖直管的长度约为米.
故答案为:.
针对训练4-4
4.项目化学习
研究课题 如何设计遮阳篷
设计要求 遮阳篷既能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.
设计方案
如图:表示直角遮阳篷.遮阳篷水平部分垂直于墙面,表示窗户.
数据收集 通过查阅相关资料和实际测量:夏至日这一天的正午时刻太阳光线与遮阳篷的夹角最大,最大角;冬至日这一天的正午时刻,太阳光线与遮阳篷的夹角最小,最小角.
问题提出 (1)如图2,若墙面的高为米,要求设计的遮阳篷正好最大限度地遮住夏天炎热的阳光,求遮阳篷水平部分的长度.(2)如图3,当窗户时,设计的遮阳篷能最大限度地遮住夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.求遮阳篷的长.(参考数据:,,,,,)
答案:(1)
(2)
解析:(1)如图1,在中,∵,,
∴,
∴,
∴的长为;
(2)如图2,在中,∵,
∴,
∴,
在中,∵,
∴,
∴,
∴,
∴,
∴遮阳篷的长为.
对边
邻边
斜边
A
C
B
对边
邻边
斜边
A
C
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
