1.2种群数量的变化课件(共31张PPT)高中生物学 人教版 选择性必修2
文档属性
| 名称 | 1.2种群数量的变化课件(共31张PPT)高中生物学 人教版 选择性必修2 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2024-12-25 11:04:05 | ||
图片预览




文档简介
(共31张PPT)
第1章 种群及其动态
1.2.1 种群数量的“J”形增长
本课内容
1. “J”形增长相关特征
“J”形增长的数学模型
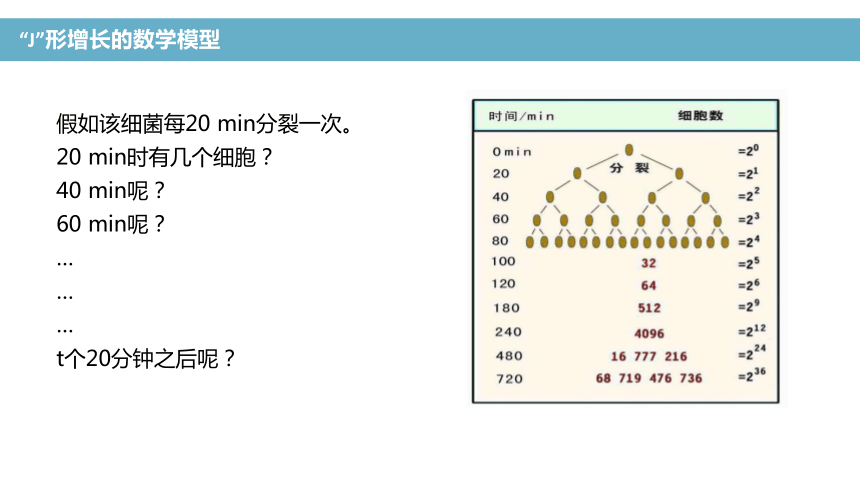
假如该细菌每20 min分裂一次。
20 min时有几个细胞?
40 min呢?
60 min呢?
…
…
…
t个20分钟之后呢?
“J”形增长的数学模型
如果初始放入的不是一个细胞,而是N0个细胞。
设该种群经历了t次分裂(即经历了t个20分钟)后的种群所含细胞数量为Nt。
请用N0、t来表示Nt 。
“J”形增长的数学模型
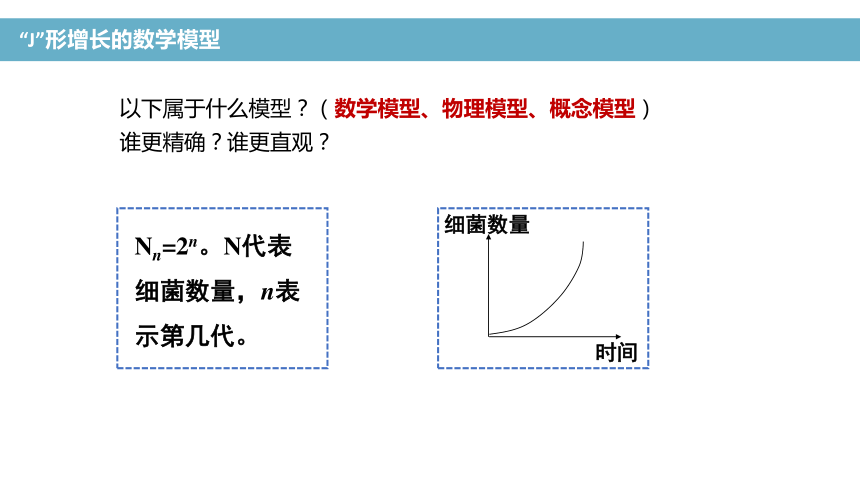
Nn=2n。N代表细菌数量,n表示第几代。
时间
细菌数量
以下属于什么模型?(数学模型、物理模型、概念模型)
谁更精确?谁更直观?
“J”形增长的数学模型
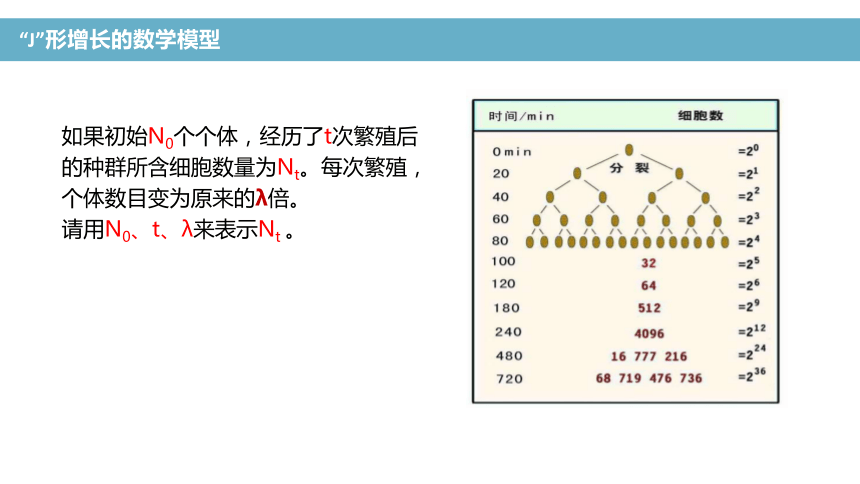
如果初始N0个个体,经历了t次繁殖后的种群所含细胞数量为Nt。每次繁殖,个体数目变为原来的λ倍。
请用N0、t、λ来表示Nt 。
“J”形增长
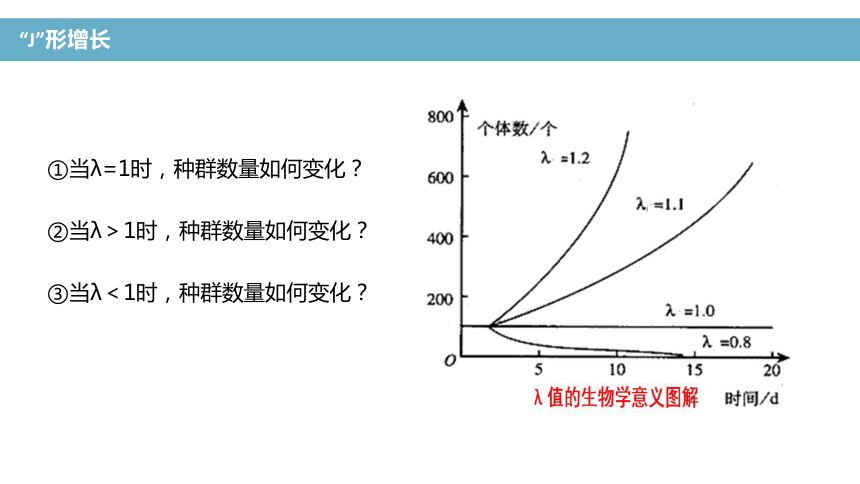
①当λ=1时,种群数量如何变化?
②当λ>1时,种群数量如何变化?
③当λ<1时,种群数量如何变化?
“J”形增长的概念
J
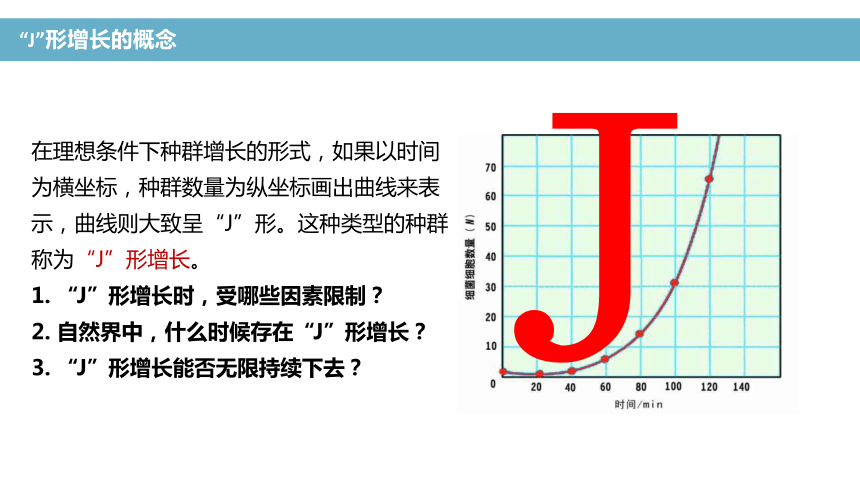
在理想条件下种群增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”形。这种类型的种群称为“J”形增长。
1. “J”形增长时,受哪些因素限制?
2. 自然界中,什么时候存在“J”形增长?
3. “J”形增长能否无限持续下去?
福寿螺
①动物迁入适宜其生活的新环境后,一段时间内种群的数量变化;
②外来入侵物种的种群数量变化;
③实验室条件。
1859年,一位来澳大利亚定居的英国人在他的农场中放生了24只野兔,一个世纪后,这24只野兔的后代竟超过6亿只
“J”形增长的案例
试一试:各段种群数量在发生什么样的变化?
“J”形增长时的λ、增长率、增长速率
时间
时间
时间
时间
种群数量
λ
增长率
增长速率
试一试
下列关于建构种群增长模型方法的说法,不正确的是(B )
A.曲线图能直观地反映出种群数量的增长趋势
B.数学模型就是用来描述一个系统或它的性质的曲线图
C.数学模型可描述、解释和预测种群数量的变化
D.在数学建模过程中也常用到假说一演绎法
第1章 种群及其动态
1.2.2 “S”形增长与数量波动
本课内容
1. S形增长相关特征
“S”形增长
生态学家高斯曾经做过单独培养大草履虫的实验:
0.5 mL培养液+5个大草履虫
每隔24h统计一次数量。
单独培养时,种群数量增长的曲线是什么形状?
“S”形增长形成的原因
分段 a-b b-c c点 c-d d-e
个体总数N
增长速率
可用的资源/空间
增长率r
形成原因
K值和K/2值
一定环境条件所能维持的种群最大数量称为环境容纳量,又称为K值。
“S”形增长最终趋于K值。
哪些因素影响K值?
K值和K/2值
个体数为K/2时,增长速率最快。因此:
1.鱼塘想获得最大的持续产出,如何捕捞?
2.防治鼠害应在曲线的什么位置进行?
“J”形增长与“S”形增长的比较
时间
时间
时间
时间
种群数量
λ
增长率
增长速率
时间
时间
时间
时间
种群数量
λ
增长率
增长速率
“J”形增长
“S”形增长
试一试
A. 当种群数量达到e点后,种群数量增长速率为0
B. 种群增长过程中出现环境阻力是在d点之后
C. 若该图表示蝗虫种群增长曲线,则虫害防治必须在C点
D. 若该图表示海洋中某种鱼的增长曲线,则最佳捕捞时间在e点
如图所示为种群在理想环境中呈“J”型增长,在有环境阻力条件下,呈“S”型增长。下列关于种群在某环境中数量增长曲线的叙述,正确的是( A)
种群数量的波动
在环境不遭受破坏的情况下, 种群数量会在 上下波动,绝非恒定不变。当种群数量偏离K值的时候,会通过 调节使种群数量回到K值。
K值会随着环境的改变而发生变化, 当环境遭受破坏时,K值变化是_______;当环境条件状况改善时,K值会_______。
种群数量的波动
特定有利条件下种群爆发:蝗灾、鼠灾、赤潮/水华等。
特定不利条件下:
人类捕杀,可能导致种群数量持续性或急剧的下降。
种群的数量过少,可能会由于近亲繁殖等而衰退、消亡(近交衰退)
为什么会有近交衰退?这提醒我们什么?
试一试
科研小组对某地甲、乙两个种群的数量进行了多年的跟踪调查,并研究Nt+1/Nt ,随时间的变化趋势,结果如图所示(图中Nt ,表示第 t 年的种群数量,Nt+1表示第t+1年的种群数量)。下列分析正确的是( B )
A. 甲种群在0~t3 段的年龄结构为增长型
B. 乙种群在0~t1 段的种群数量呈“J”形增长
C. 乙种群在t2 时数量最少
D. 甲种群在t3 后数量相对稳定可能是生存条件得到了改善
第1章 种群及其动态
1.2.3 种群数量各类曲线
K值变化
C
K值变化
B
围绕K值波动
A
增长速率图像
B
增长速率图像
D
增长速率图像
C
增长率/λ图像
C
第1章 种群及其动态
1.2.1 种群数量的“J”形增长
本课内容
1. “J”形增长相关特征
“J”形增长的数学模型
假如该细菌每20 min分裂一次。
20 min时有几个细胞?
40 min呢?
60 min呢?
…
…
…
t个20分钟之后呢?
“J”形增长的数学模型
如果初始放入的不是一个细胞,而是N0个细胞。
设该种群经历了t次分裂(即经历了t个20分钟)后的种群所含细胞数量为Nt。
请用N0、t来表示Nt 。
“J”形增长的数学模型
Nn=2n。N代表细菌数量,n表示第几代。
时间
细菌数量
以下属于什么模型?(数学模型、物理模型、概念模型)
谁更精确?谁更直观?
“J”形增长的数学模型
如果初始N0个个体,经历了t次繁殖后的种群所含细胞数量为Nt。每次繁殖,个体数目变为原来的λ倍。
请用N0、t、λ来表示Nt 。
“J”形增长
①当λ=1时,种群数量如何变化?
②当λ>1时,种群数量如何变化?
③当λ<1时,种群数量如何变化?
“J”形增长的概念
J
在理想条件下种群增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”形。这种类型的种群称为“J”形增长。
1. “J”形增长时,受哪些因素限制?
2. 自然界中,什么时候存在“J”形增长?
3. “J”形增长能否无限持续下去?
福寿螺
①动物迁入适宜其生活的新环境后,一段时间内种群的数量变化;
②外来入侵物种的种群数量变化;
③实验室条件。
1859年,一位来澳大利亚定居的英国人在他的农场中放生了24只野兔,一个世纪后,这24只野兔的后代竟超过6亿只
“J”形增长的案例
试一试:各段种群数量在发生什么样的变化?
“J”形增长时的λ、增长率、增长速率
时间
时间
时间
时间
种群数量
λ
增长率
增长速率
试一试
下列关于建构种群增长模型方法的说法,不正确的是(B )
A.曲线图能直观地反映出种群数量的增长趋势
B.数学模型就是用来描述一个系统或它的性质的曲线图
C.数学模型可描述、解释和预测种群数量的变化
D.在数学建模过程中也常用到假说一演绎法
第1章 种群及其动态
1.2.2 “S”形增长与数量波动
本课内容
1. S形增长相关特征
“S”形增长
生态学家高斯曾经做过单独培养大草履虫的实验:
0.5 mL培养液+5个大草履虫
每隔24h统计一次数量。
单独培养时,种群数量增长的曲线是什么形状?
“S”形增长形成的原因
分段 a-b b-c c点 c-d d-e
个体总数N
增长速率
可用的资源/空间
增长率r
形成原因
K值和K/2值
一定环境条件所能维持的种群最大数量称为环境容纳量,又称为K值。
“S”形增长最终趋于K值。
哪些因素影响K值?
K值和K/2值
个体数为K/2时,增长速率最快。因此:
1.鱼塘想获得最大的持续产出,如何捕捞?
2.防治鼠害应在曲线的什么位置进行?
“J”形增长与“S”形增长的比较
时间
时间
时间
时间
种群数量
λ
增长率
增长速率
时间
时间
时间
时间
种群数量
λ
增长率
增长速率
“J”形增长
“S”形增长
试一试
A. 当种群数量达到e点后,种群数量增长速率为0
B. 种群增长过程中出现环境阻力是在d点之后
C. 若该图表示蝗虫种群增长曲线,则虫害防治必须在C点
D. 若该图表示海洋中某种鱼的增长曲线,则最佳捕捞时间在e点
如图所示为种群在理想环境中呈“J”型增长,在有环境阻力条件下,呈“S”型增长。下列关于种群在某环境中数量增长曲线的叙述,正确的是( A)
种群数量的波动
在环境不遭受破坏的情况下, 种群数量会在 上下波动,绝非恒定不变。当种群数量偏离K值的时候,会通过 调节使种群数量回到K值。
K值会随着环境的改变而发生变化, 当环境遭受破坏时,K值变化是_______;当环境条件状况改善时,K值会_______。
种群数量的波动
特定有利条件下种群爆发:蝗灾、鼠灾、赤潮/水华等。
特定不利条件下:
人类捕杀,可能导致种群数量持续性或急剧的下降。
种群的数量过少,可能会由于近亲繁殖等而衰退、消亡(近交衰退)
为什么会有近交衰退?这提醒我们什么?
试一试
科研小组对某地甲、乙两个种群的数量进行了多年的跟踪调查,并研究Nt+1/Nt ,随时间的变化趋势,结果如图所示(图中Nt ,表示第 t 年的种群数量,Nt+1表示第t+1年的种群数量)。下列分析正确的是( B )
A. 甲种群在0~t3 段的年龄结构为增长型
B. 乙种群在0~t1 段的种群数量呈“J”形增长
C. 乙种群在t2 时数量最少
D. 甲种群在t3 后数量相对稳定可能是生存条件得到了改善
第1章 种群及其动态
1.2.3 种群数量各类曲线
K值变化
C
K值变化
B
围绕K值波动
A
增长速率图像
B
增长速率图像
D
增长速率图像
C
增长率/λ图像
C
