人教版2024-2025学年八年级下学期期末考试数学试卷
文档属性
| 名称 | 人教版2024-2025学年八年级下学期期末考试数学试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 22:26:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年下学期期末试卷
八年级数学
一、选择题(每小题3分,共30分)
1.若在实数范围内有意义,则实数的取值范围是( )
A. B. C. D.
2.在下列计算中,正确的是( )
A. B. C. D.
3.如图,已知,且,,,则、两点间的距离是( )
A. B.20 C. D.24
4.已知一组数据,,,,的平均数是2,方差是2,那另一组数据,,,,,的平均数和方差分别为( )
A.4,4 B.3,3 C.3,8 D.3,4
5.如图,在中,,垂足为,,垂足为.若,的周长为20,则的长为( )
A.4 B.5 C.6 D.8
6.如图,正方形的对角线,交于点,是边上一点,连接,过点作,交于点.若四边形的面积是1,则的长为( )
A.1 B. C.2 D.
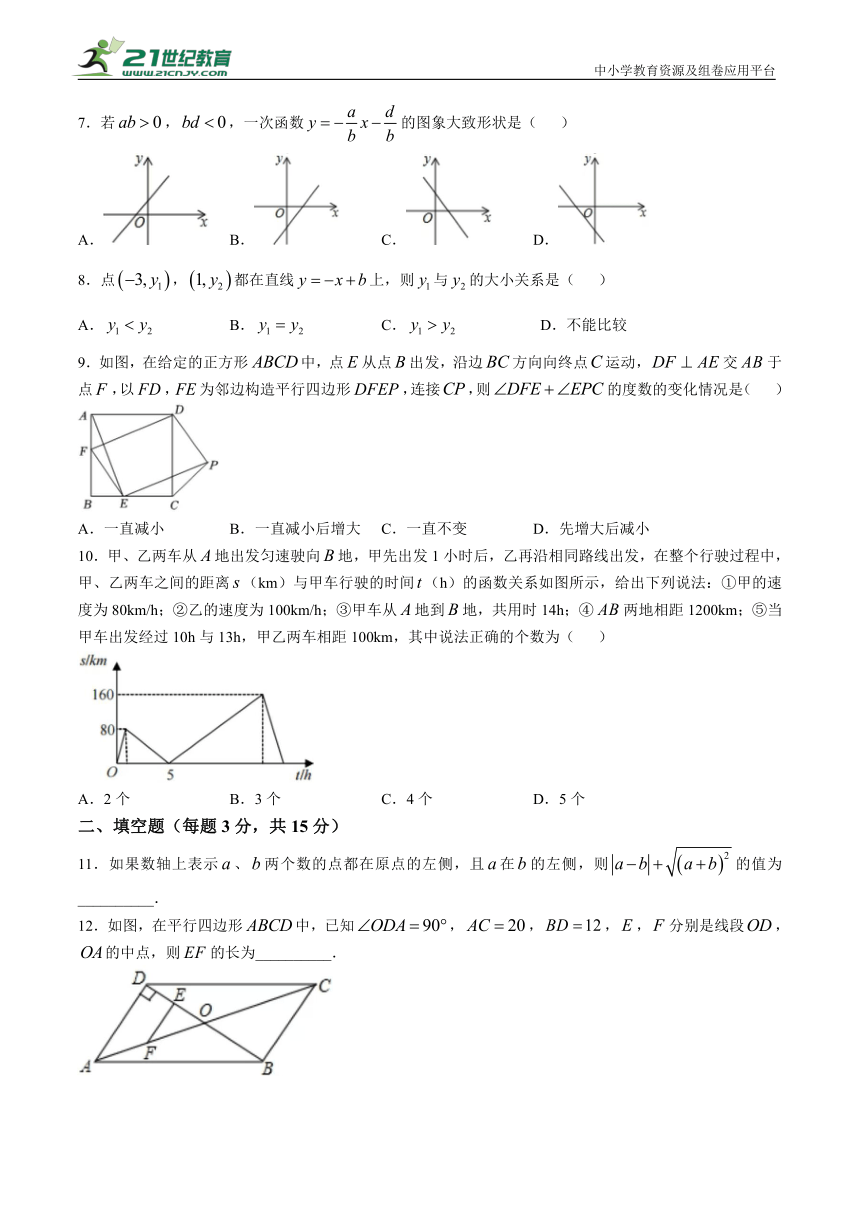
7.若,,一次函数的图象大致形状是( )
A. B. C. D.
8.点,都在直线上,则与的大小关系是( )
A. B. C. D.不能比较
9.如图,在给定的正方形中,点从点出发,沿边方向向终点运动,交于点,以,为邻边构造平行四边形,连接,则的度数的变化情况是( )
A.一直减小 B.一直减小后增大 C.一直不变 D.先增大后减小
10.甲、乙两车从地出发匀速驶向地,甲先出发1小时后,乙再沿相同路线出发,在整个行驶过程中,甲、乙两车之间的距离(km)与甲车行驶的时间(h)的函数关系如图所示,给出下列说法:①甲的速度为80km/h;②乙的速度为100km/h;③甲车从地到地,共用时14h;④两地相距1200km;⑤当甲车出发经过10h与13h,甲乙两车相距100km,其中说法正确的个数为( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每题3分,共15分)
11.如果数轴上表示、两个数的点都在原点的左侧,且在的左侧,则的值为__________.
12.如图,在平行四边形中,已知,,,,分别是线段,的中点,则的长为__________.
13.已知,是直线上的相异两点,若,则的取值范围是__________.
14.如图,直线经过点和点,直线过点,则不等式的解集为__________.
15.如图,矩形中,,,点是边上一点,连接,把沿折叠,使点落在点处,当为直角三角形时,的长为__________.
三、解答题(共76分)
16.(每小题4分共8分)计算:
(1) (2)已知,,求的值.
17.(9分)为了调查全校学生对垃圾分类知识的了解情况,小胡和小叶同学分别随机抽取了20名男生和20名女生进行了相关知识测试,获得了数据(成绩)(百分制,单位:分),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息.
收集数据:
20名男生的成绩统计(单位:分)
76 82 78 86 60 92 76 80 98 72 78 96 75 100 82 87 70 54 87 78
20名女生的成绩统计(单位:分)
97 95 90 68 78 80 68 94 86 80 87 92 59 75 93 86 56 76 86 70
整理数据:(成绩得分用表示)
成绩
男生(人数) 1 1 8 6 4
女生(人数) 2 6 6
分析数据:
平均数 中位数 众数
男生 80.35 79 78
女生 80.8
请回答下列问题:
(1)上述两表中,__________;__________,__________,__________.
(2)你认为男生和女生对垃圾分类知识的了解情况哪个更好一些,并利用数据说明理由;
(3)若此次成绩不低于80分为优秀,请估计全校800人中优秀人数为多少?
18.(9分)一艘轮船从港向南偏西48°方向航行100km到达岛,再从岛沿方向航行125km到达岛,港到航线的最短距离是60km.
(1)若轮船速度为25km/小时,求轮船从岛沿返回港所需的时间.
(2)岛在港的什么方向?
19.(9分)如图,在中,点、分别是、的中点,分别连接、、.
(1)求证:;
(2)当满足什么条件时,四边形是菱形,请说明理由.
20.(9分)如图,在平面直角坐标系中,一次函数的图象经过点,且与轴相交于点,与正比例函数的图象相交于点,点的横坐标为1.
(1)求一次函数的解析式;
(2)若点在轴上,且满足,请直接写出点的坐标.
21.(10分)我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.
(1)求甲、乙两种奖品的单价;
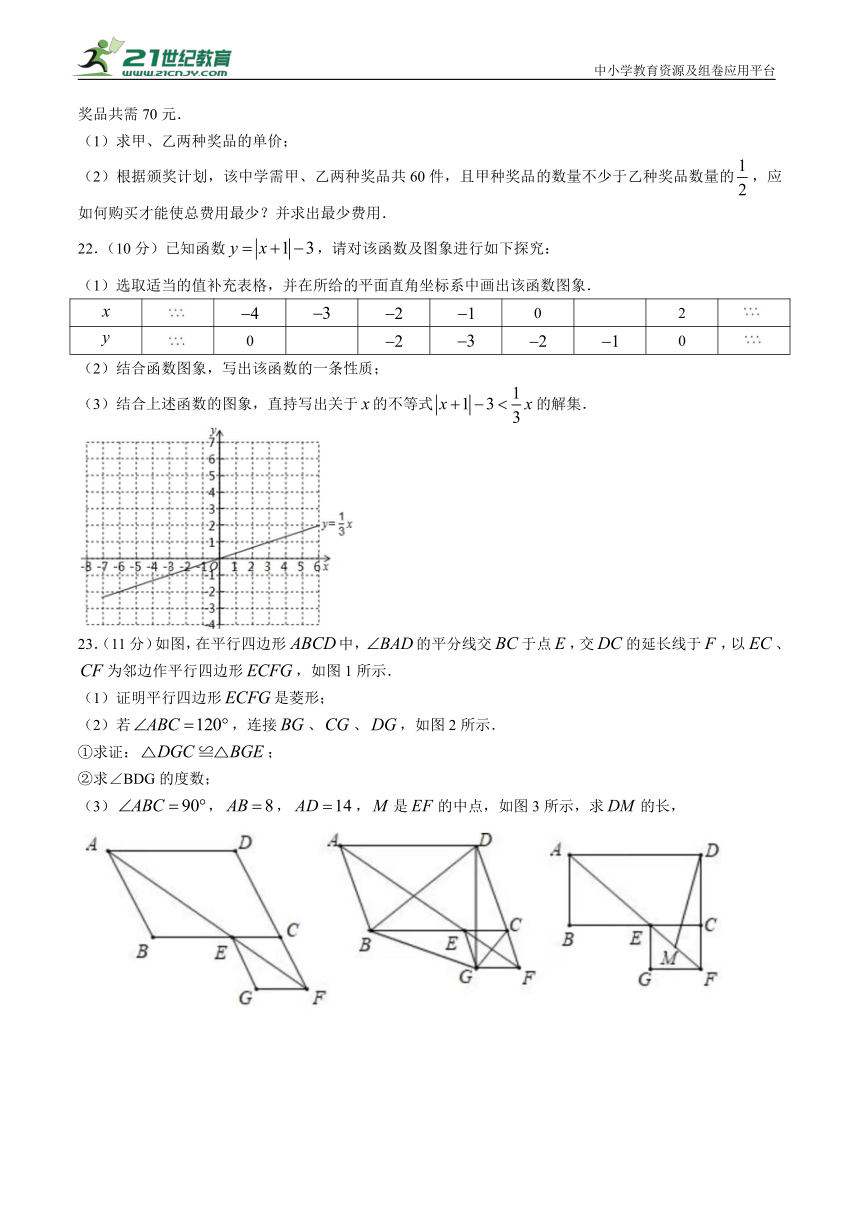
(2)根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的,应如何购买才能使总费用最少?并求出最少费用.
22.(10分)已知函数,请对该函数及图象进行如下探究:
(1)选取适当的值补充表格,并在所给的平面直角坐标系中画出该函数图象.
0 2
0 0
(2)结合函数图象,写出该函数的一条性质;
(3)结合上述函数的图象,直持写出关于的不等式的解集.
23.(11分)如图,在平行四边形中,的平分线交于点,交的延长线于,以、为邻边作平行四边形,如图1所示.
(1)证明平行四边形是菱形;
(2)若,连接、、,如图2所示.
①求证:;
②求∠BDG的度数;
(3),,,是的中点,如图3所示,求的长,
参考答案
1.A 2.D 3.B 4.C 5.A 6.C 7.C 8.C 9.C 10.C
11. 12.4 13. 14. 15.3或
16.(1)5 (2)
三、16.(1)原式
(2),,
则.
17.如下
(1)由表中的数据得:,,
20名女生的成绩从小到大排列为:
56 59 68 68 70 75 76 78 80 80 86 86 86 87 90 92 93 94 95 97
排在中间的两个数是88和89,
;
出现次数最多的是86分,因此众数是86,即,
故答案为:2,4,83,86;
(2)女生对垃圾分类知识的了解情况更好一些理由如下:
从平均数、中位数和众数上看女生的较高,
女生对垃圾分类知识的了解情况更好一些;
(3)(人)
答:估计全校800人中优秀人数为440人.
18.如下
(1)由题意km
中,,得
(km)
(km)
在中,
(km)
则有(小时)
从岛返回港所需的时间为3小时
(2),
在中,
在港的南偏西48°方向,
岛在港的北偏西42°
19.如下
(1)证明:四边形是平行四边形,
,,,
点、分别是、的中点,
,.
.
在与中,
20.如下
(1)当时,,
点的坐标为,
将、代入,
得:
解得:
一次函数的解析式为;
(2)当时,有,
解得:,
点的坐标为.
设点的坐标为,
,即
,
解得:,
点的坐标为或.
21.如下
(1)设甲种奖品的单价为元/件,乙种奖品的单价为元/件,
依题意,得:
解得:,
答:甲种奖品的单价为20元/件,乙种奖品的单价为10元/件.
(2)设购买甲种奖品件,则购买乙种奖品件,设购买两种奖品的总费用为元,
甲种奖品的数量不少于乙种奖品的数量的,
,
.
依题意,得:,
,
随值的增大而增大,
当学校购买20件甲种奖品、40件乙种奖品时,总费用最少,最少费用是800元.
22.(1)如图
0 1 2
0 0
(2)性质不唯一,时随的增大而增大,
时随的增大而减小等.
(3)根据图象可知:关于的不等式的解集:.
23.如下
(1)平分,
,
四边形是平行四边形,
,,
,,
,
,
又四边形是平行四边形,
四边形为菱形;
(2)①四边形是平行四边形,
,,,
,
,
,
,
由(1)知,四边形是菱形,
,,
,
为等边三角形,
,
,
,
,
,
是的平分线,
,
,
,
,
,
,
在和中,
;
②,
,,
,
,
是等边三角形,
,
,
,
是等边三角形,
;
(3)如图所示:
连接,,
,四边形是平行四边形,
四边形是矩形,
,
又由(1)可知四边形为菱形,
,
四边形为正方形.
,
,
为中点,
,
,
在和中,
.
,.
是等腰直角三角形,
,,
在中,,
,
.
2024-2025学年下学期期末试卷
八年级数学
一、选择题(每小题3分,共30分)
1.若在实数范围内有意义,则实数的取值范围是( )
A. B. C. D.
2.在下列计算中,正确的是( )
A. B. C. D.
3.如图,已知,且,,,则、两点间的距离是( )
A. B.20 C. D.24
4.已知一组数据,,,,的平均数是2,方差是2,那另一组数据,,,,,的平均数和方差分别为( )
A.4,4 B.3,3 C.3,8 D.3,4
5.如图,在中,,垂足为,,垂足为.若,的周长为20,则的长为( )
A.4 B.5 C.6 D.8
6.如图,正方形的对角线,交于点,是边上一点,连接,过点作,交于点.若四边形的面积是1,则的长为( )
A.1 B. C.2 D.
7.若,,一次函数的图象大致形状是( )
A. B. C. D.
8.点,都在直线上,则与的大小关系是( )
A. B. C. D.不能比较
9.如图,在给定的正方形中,点从点出发,沿边方向向终点运动,交于点,以,为邻边构造平行四边形,连接,则的度数的变化情况是( )
A.一直减小 B.一直减小后增大 C.一直不变 D.先增大后减小
10.甲、乙两车从地出发匀速驶向地,甲先出发1小时后,乙再沿相同路线出发,在整个行驶过程中,甲、乙两车之间的距离(km)与甲车行驶的时间(h)的函数关系如图所示,给出下列说法:①甲的速度为80km/h;②乙的速度为100km/h;③甲车从地到地,共用时14h;④两地相距1200km;⑤当甲车出发经过10h与13h,甲乙两车相距100km,其中说法正确的个数为( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每题3分,共15分)
11.如果数轴上表示、两个数的点都在原点的左侧,且在的左侧,则的值为__________.
12.如图,在平行四边形中,已知,,,,分别是线段,的中点,则的长为__________.
13.已知,是直线上的相异两点,若,则的取值范围是__________.
14.如图,直线经过点和点,直线过点,则不等式的解集为__________.
15.如图,矩形中,,,点是边上一点,连接,把沿折叠,使点落在点处,当为直角三角形时,的长为__________.
三、解答题(共76分)
16.(每小题4分共8分)计算:
(1) (2)已知,,求的值.
17.(9分)为了调查全校学生对垃圾分类知识的了解情况,小胡和小叶同学分别随机抽取了20名男生和20名女生进行了相关知识测试,获得了数据(成绩)(百分制,单位:分),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息.
收集数据:
20名男生的成绩统计(单位:分)
76 82 78 86 60 92 76 80 98 72 78 96 75 100 82 87 70 54 87 78
20名女生的成绩统计(单位:分)
97 95 90 68 78 80 68 94 86 80 87 92 59 75 93 86 56 76 86 70
整理数据:(成绩得分用表示)
成绩
男生(人数) 1 1 8 6 4
女生(人数) 2 6 6
分析数据:
平均数 中位数 众数
男生 80.35 79 78
女生 80.8
请回答下列问题:
(1)上述两表中,__________;__________,__________,__________.
(2)你认为男生和女生对垃圾分类知识的了解情况哪个更好一些,并利用数据说明理由;
(3)若此次成绩不低于80分为优秀,请估计全校800人中优秀人数为多少?
18.(9分)一艘轮船从港向南偏西48°方向航行100km到达岛,再从岛沿方向航行125km到达岛,港到航线的最短距离是60km.
(1)若轮船速度为25km/小时,求轮船从岛沿返回港所需的时间.
(2)岛在港的什么方向?
19.(9分)如图,在中,点、分别是、的中点,分别连接、、.
(1)求证:;
(2)当满足什么条件时,四边形是菱形,请说明理由.
20.(9分)如图,在平面直角坐标系中,一次函数的图象经过点,且与轴相交于点,与正比例函数的图象相交于点,点的横坐标为1.
(1)求一次函数的解析式;
(2)若点在轴上,且满足,请直接写出点的坐标.
21.(10分)我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.
(1)求甲、乙两种奖品的单价;
(2)根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的,应如何购买才能使总费用最少?并求出最少费用.
22.(10分)已知函数,请对该函数及图象进行如下探究:
(1)选取适当的值补充表格,并在所给的平面直角坐标系中画出该函数图象.
0 2
0 0
(2)结合函数图象,写出该函数的一条性质;
(3)结合上述函数的图象,直持写出关于的不等式的解集.
23.(11分)如图,在平行四边形中,的平分线交于点,交的延长线于,以、为邻边作平行四边形,如图1所示.
(1)证明平行四边形是菱形;
(2)若,连接、、,如图2所示.
①求证:;
②求∠BDG的度数;
(3),,,是的中点,如图3所示,求的长,
参考答案
1.A 2.D 3.B 4.C 5.A 6.C 7.C 8.C 9.C 10.C
11. 12.4 13. 14. 15.3或
16.(1)5 (2)
三、16.(1)原式
(2),,
则.
17.如下
(1)由表中的数据得:,,
20名女生的成绩从小到大排列为:
56 59 68 68 70 75 76 78 80 80 86 86 86 87 90 92 93 94 95 97
排在中间的两个数是88和89,
;
出现次数最多的是86分,因此众数是86,即,
故答案为:2,4,83,86;
(2)女生对垃圾分类知识的了解情况更好一些理由如下:
从平均数、中位数和众数上看女生的较高,
女生对垃圾分类知识的了解情况更好一些;
(3)(人)
答:估计全校800人中优秀人数为440人.
18.如下
(1)由题意km
中,,得
(km)
(km)
在中,
(km)
则有(小时)
从岛返回港所需的时间为3小时
(2),
在中,
在港的南偏西48°方向,
岛在港的北偏西42°
19.如下
(1)证明:四边形是平行四边形,
,,,
点、分别是、的中点,
,.
.
在与中,
20.如下
(1)当时,,
点的坐标为,
将、代入,
得:
解得:
一次函数的解析式为;
(2)当时,有,
解得:,
点的坐标为.
设点的坐标为,
,即
,
解得:,
点的坐标为或.
21.如下
(1)设甲种奖品的单价为元/件,乙种奖品的单价为元/件,
依题意,得:
解得:,
答:甲种奖品的单价为20元/件,乙种奖品的单价为10元/件.
(2)设购买甲种奖品件,则购买乙种奖品件,设购买两种奖品的总费用为元,
甲种奖品的数量不少于乙种奖品的数量的,
,
.
依题意,得:,
,
随值的增大而增大,
当学校购买20件甲种奖品、40件乙种奖品时,总费用最少,最少费用是800元.
22.(1)如图
0 1 2
0 0
(2)性质不唯一,时随的增大而增大,
时随的增大而减小等.
(3)根据图象可知:关于的不等式的解集:.
23.如下
(1)平分,
,
四边形是平行四边形,
,,
,,
,
,
又四边形是平行四边形,
四边形为菱形;
(2)①四边形是平行四边形,
,,,
,
,
,
,
由(1)知,四边形是菱形,
,,
,
为等边三角形,
,
,
,
,
,
是的平分线,
,
,
,
,
,
,
在和中,
;
②,
,,
,
,
是等边三角形,
,
,
,
是等边三角形,
;
(3)如图所示:
连接,,
,四边形是平行四边形,
四边形是矩形,
,
又由(1)可知四边形为菱形,
,
四边形为正方形.
,
,
为中点,
,
,
在和中,
.
,.
是等腰直角三角形,
,,
在中,,
,
.
同课章节目录
