2023-2024学年上海行知中学高二上学期数学期末试卷(2024.01)(PDF版,含答案)
文档属性
| 名称 | 2023-2024学年上海行知中学高二上学期数学期末试卷(2024.01)(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 557.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-25 07:18:21 | ||
图片预览




文档简介
行知2023学年第一学期高二年级数学期末
2024.01
一、填空题(本题满分54分,共有12题,1-6每题4分,7-12每题5分)
1。双曲线写-少广=1的焦点坐标是
2.已知事件A与事件B相互独立,且P(A)=0.3,P(B)=0.6,则P(A∩B)=
3.已知一个等比数列的第4项是号,公比是-了,它的第1项是
1
4,一组数据3,6,8,4,10,15,18的平均数为10,则该数据的中位数是
5.在四面体P-ABC中,若底面ABC的一个法向量为n=(1,1,1),且CP=(2,2,-1),则
顶点P到底面ABC的距离为一·
6.已知直线:y=kx+2经过点(1,1),则直线1倾斜角的大小为
7.如图,正方体ABCD-A,BC,D中,AB=BC=6,点E在线
D E
C
B
段C,D上,且2D,E=EC1,M为线段BE的中点,若BE=2W14,
M
D
则异面直线AD,与CM所成角的余弦值为
的
8,某新学校高一、高二、高三共有学生950名,为了了解同学们的兴趣爱好,计划采用分
层抽样的方法,从这950名学生中抽取一个样本容量为190的样本,若从高一、高二、高
三拍取的人数恰好组成一个以号为公比的等比数列,则此学校商一年级的学生人数
为
9.已知直线x-y=1与圆x2+y2+2gy+1=0(a>0)没有公共点,则a的取值范围是
10.在四棱锥P-ABCD中,底面ABCD为正方形,PA=AB=2,M为空间中一动点,G
为PC的中点,PA⊥平面ABCD·若MA.MG=0,则M的轨迹围成封闭图形的体积
为
11.已知点P是曲线ax2+y2=1(其中a,b为常数)上的一点,设M,N是直线y=x
上任意两个不同的点,且MW=t,则下列结论正确的是
①当ab>0时,方程ax2+y2=1表示椭圆;
②当ab<0时,方程cx2+b2=1表示双曲线;
③当a=4,b-令,且1-4时,且1-4时,使得△MNP是等腰直角三角形的点P有6
个;
1
1
③当a=
24b=g,且0<1<4时,使得aMNP是等腰直角三角形的点P有8个.
M
G
A
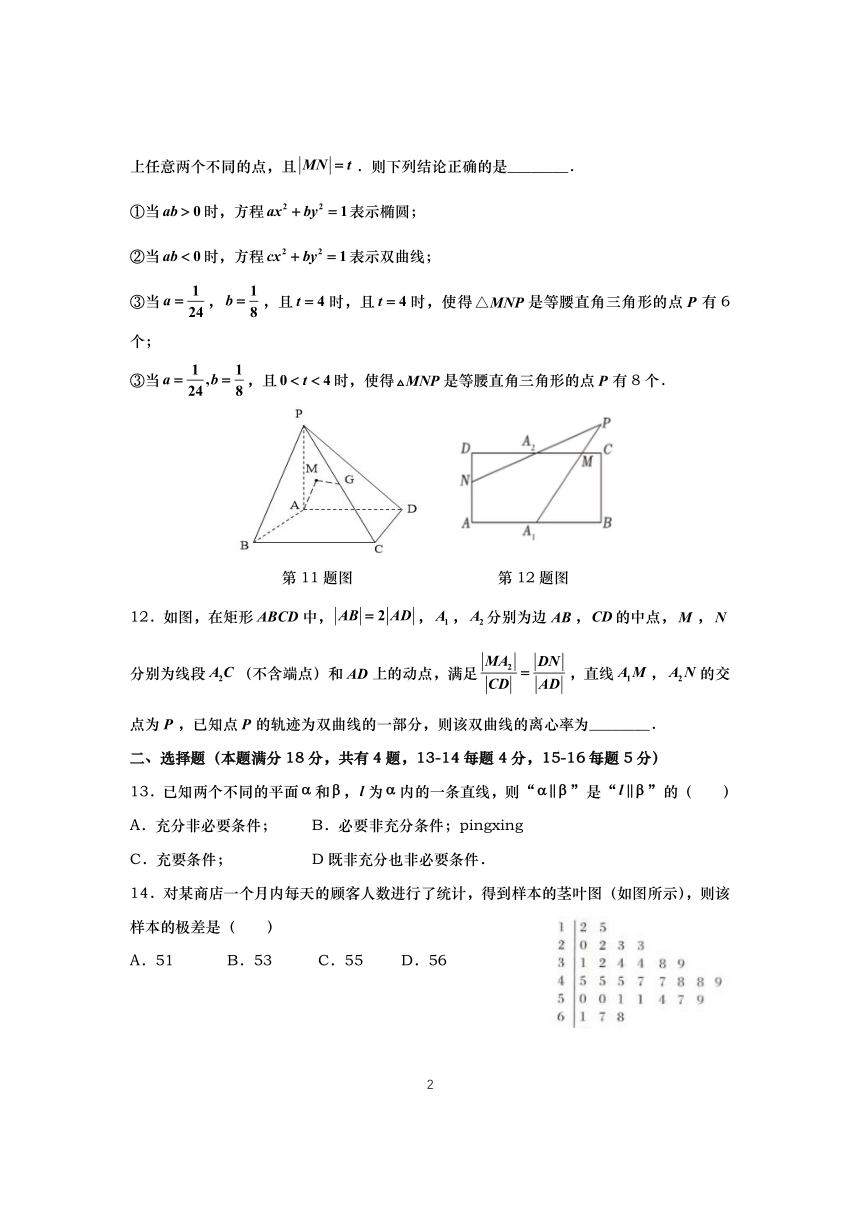
第11题图
第12题图
12.如图,在矩形ABCD中,AB=2AD,A,A分别为边AB,CD的中点,M,N
MA DN
分别为线段A,C(不含端点)和AD上的动点,满足
CD=HD,直线AM,AN的交
点为P,已知点P的轨迹为双曲线的一部分,则该双曲线的离心率为。
二、选择题(本题满分18分,共有4题,13-14每题4分,15-16每题5分)
13.已知两个不同的平面a和B,1为a内的一条直线,则“aB”是“I川B”的()
A.充分非必要条件;
B.必要非充分条件;pingxing
C.充要条件;
D既非充分也非必要条件.
14,对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该
样本的极差是()
1125
20233
A.51
B.53
C.55
D.56
3124489
455577889
50011479
6178
2024.01
一、填空题(本题满分54分,共有12题,1-6每题4分,7-12每题5分)
1。双曲线写-少广=1的焦点坐标是
2.已知事件A与事件B相互独立,且P(A)=0.3,P(B)=0.6,则P(A∩B)=
3.已知一个等比数列的第4项是号,公比是-了,它的第1项是
1
4,一组数据3,6,8,4,10,15,18的平均数为10,则该数据的中位数是
5.在四面体P-ABC中,若底面ABC的一个法向量为n=(1,1,1),且CP=(2,2,-1),则
顶点P到底面ABC的距离为一·
6.已知直线:y=kx+2经过点(1,1),则直线1倾斜角的大小为
7.如图,正方体ABCD-A,BC,D中,AB=BC=6,点E在线
D E
C
B
段C,D上,且2D,E=EC1,M为线段BE的中点,若BE=2W14,
M
D
则异面直线AD,与CM所成角的余弦值为
的
8,某新学校高一、高二、高三共有学生950名,为了了解同学们的兴趣爱好,计划采用分
层抽样的方法,从这950名学生中抽取一个样本容量为190的样本,若从高一、高二、高
三拍取的人数恰好组成一个以号为公比的等比数列,则此学校商一年级的学生人数
为
9.已知直线x-y=1与圆x2+y2+2gy+1=0(a>0)没有公共点,则a的取值范围是
10.在四棱锥P-ABCD中,底面ABCD为正方形,PA=AB=2,M为空间中一动点,G
为PC的中点,PA⊥平面ABCD·若MA.MG=0,则M的轨迹围成封闭图形的体积
为
11.已知点P是曲线ax2+y2=1(其中a,b为常数)上的一点,设M,N是直线y=x
上任意两个不同的点,且MW=t,则下列结论正确的是
①当ab>0时,方程ax2+y2=1表示椭圆;
②当ab<0时,方程cx2+b2=1表示双曲线;
③当a=4,b-令,且1-4时,且1-4时,使得△MNP是等腰直角三角形的点P有6
个;
1
1
③当a=
24b=g,且0<1<4时,使得aMNP是等腰直角三角形的点P有8个.
M
G
A
第11题图
第12题图
12.如图,在矩形ABCD中,AB=2AD,A,A分别为边AB,CD的中点,M,N
MA DN
分别为线段A,C(不含端点)和AD上的动点,满足
CD=HD,直线AM,AN的交
点为P,已知点P的轨迹为双曲线的一部分,则该双曲线的离心率为。
二、选择题(本题满分18分,共有4题,13-14每题4分,15-16每题5分)
13.已知两个不同的平面a和B,1为a内的一条直线,则“aB”是“I川B”的()
A.充分非必要条件;
B.必要非充分条件;pingxing
C.充要条件;
D既非充分也非必要条件.
14,对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该
样本的极差是()
1125
20233
A.51
B.53
C.55
D.56
3124489
455577889
50011479
6178
同课章节目录
