八年级下第18章平行四边形单元测试题含答案
文档属性
| 名称 | 八年级下第18章平行四边形单元测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-09 18:07:00 | ||
图片预览


文档简介
平行四边形单元测试
选择题(每题3分)
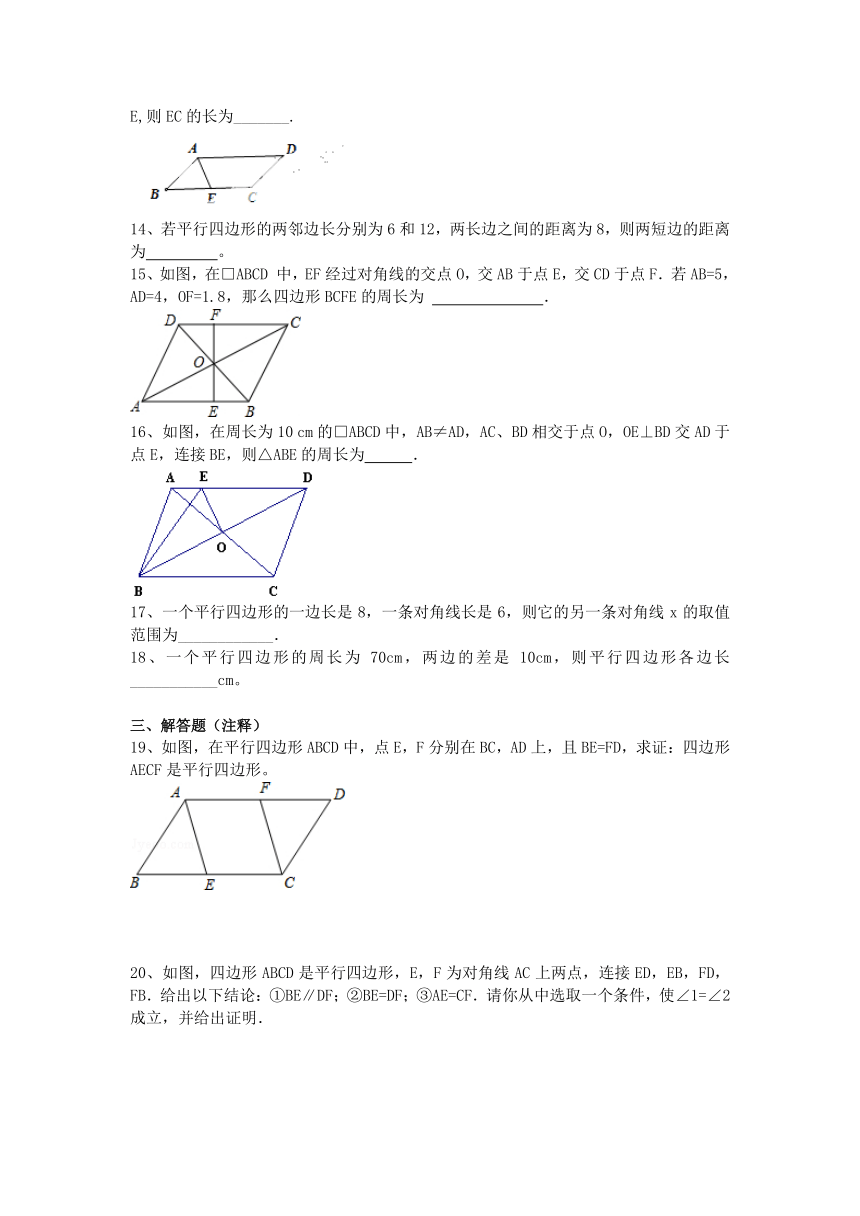
1、如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=( )
A.150° B.40° C.80° D.90°
2、若平行四边形的一边和一条对角线长都是10cm,则另一条对角线长可以是( )
A.5cm B.10cm C.20cm D.30cm
3、如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
4、如图所示,O为平行四边形ABCD两对角线的交点,图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
5、如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a-b)等于( )
A.4 B.5 C.6 D.7
6、如图,平行四边形ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( )
A.16° B.22° C.32° D.68°
7、平行四边形一边长为12,那么这个平行四边形的两条对角线的长可能是( )A.8和12 B.9和13 C.12和12 D.11和14
8、如图,□的周长是,△ABC的周长是,则的长为( )
A. B. C. D.
9、如图,在□中,,,的垂直平分线交于点,则△的周长是( )
A.6 B.8 C.9 D.10
填空题(每题3分)
10、如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是 (只填写一个条件,不使用图形以外的字母和线段).
11、已知在平行四边形ABCD中,对角线BD=14,过平行四边形ABCD的顶点D作高,垂足为H,连接OH,则OH= .
12、如图,在□ABCD中,CE⊥AB于E,如果∠A=125°,那么∠BCE= °.
13、如图,在平行四边形ABCD中,已知AD=9㎝,AB=5㎝,AE平分∠BAD交BC边于点E,则EC的长为_______.
14、若平行四边形的两邻边长分别为6和12,两长边之间的距离为8,则两短边的距离为 。
15、如图,在□ABCD 中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为 .
16、如图,在周长为10 cm的□ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为 .
17、一个平行四边形的一边长是8,一条对角线长是6,则它的另一条对角线x的取值范围为____________.
18、一个平行四边形的周长为70cm,两边的差是10cm,则平行四边形各边长___________cm。
三、解答题(注释)
19、如图,在平行四边形ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形。
20、如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
21、如图,在?ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.求证:AB=BF.
22、如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
23、如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
参考答案
一、选择题
1、D 2、C 3、A. 4、D. 5、C. 6、C. 7、D 8、D 9、B
二、填空题
10、AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等
11、7 12、35 13、4cm 14、16 15、12.6. 16、5cm. 17、10<x<22.
18、22.5cm,12.5cm,22.5cm,12.5cm.
三、解答题
19、【答案】详见解析
20、【答案】解:方法一:
补充条件①BE∥DF.
证明:如图,∵BE∥DF,
∴∠BEC=∠DFA,
∴∠BEA=∠DFC,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴四边形BFDE是平行四边形,
∴ED∥BF,
∴∠1=∠2;
方法二:
补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS),
∴∠1=∠2.
21、【答案】证明:由ABCD是平行四边形得AB∥CD,
∴∠CDE=∠F,∠C=∠EBF.
又∵E为BC的中点,
∴△DEC≌△FEB,
∴DC=FB.
又∵AB=CD,
∴AB=BF.
22、【答案】证明见解析.
根据两条对角线相互平分的四边形是平行四边形即可证明四边形AECF是平行四边形.
连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF为平行四边形.
23、【答案】本题是关于平行四边形的判定,判定方法有五种:?定义:两组对边分别平行的四边形是平行四边形;?两组对边分别相等的四边形是平行四边形?一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;⑤两组对角分别相等的四边形是平行四边形.找出合适的条件即可,此种类型题常有多种证法.举一证法如下:
试题解析:证明:∵BE⊥AD,BE⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,BE⊥AD,
∴BE∥CF
∴四边形BECF是平行四边形.
选择题(每题3分)
1、如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=( )
A.150° B.40° C.80° D.90°
2、若平行四边形的一边和一条对角线长都是10cm,则另一条对角线长可以是( )
A.5cm B.10cm C.20cm D.30cm
3、如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
4、如图所示,O为平行四边形ABCD两对角线的交点,图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
5、如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a-b)等于( )
A.4 B.5 C.6 D.7
6、如图,平行四边形ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( )
A.16° B.22° C.32° D.68°
7、平行四边形一边长为12,那么这个平行四边形的两条对角线的长可能是( )A.8和12 B.9和13 C.12和12 D.11和14
8、如图,□的周长是,△ABC的周长是,则的长为( )
A. B. C. D.
9、如图,在□中,,,的垂直平分线交于点,则△的周长是( )
A.6 B.8 C.9 D.10
填空题(每题3分)
10、如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是 (只填写一个条件,不使用图形以外的字母和线段).
11、已知在平行四边形ABCD中,对角线BD=14,过平行四边形ABCD的顶点D作高,垂足为H,连接OH,则OH= .
12、如图,在□ABCD中,CE⊥AB于E,如果∠A=125°,那么∠BCE= °.
13、如图,在平行四边形ABCD中,已知AD=9㎝,AB=5㎝,AE平分∠BAD交BC边于点E,则EC的长为_______.
14、若平行四边形的两邻边长分别为6和12,两长边之间的距离为8,则两短边的距离为 。
15、如图,在□ABCD 中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为 .
16、如图,在周长为10 cm的□ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为 .
17、一个平行四边形的一边长是8,一条对角线长是6,则它的另一条对角线x的取值范围为____________.
18、一个平行四边形的周长为70cm,两边的差是10cm,则平行四边形各边长___________cm。
三、解答题(注释)
19、如图,在平行四边形ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形。
20、如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
21、如图,在?ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.求证:AB=BF.
22、如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
23、如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
参考答案
一、选择题
1、D 2、C 3、A. 4、D. 5、C. 6、C. 7、D 8、D 9、B
二、填空题
10、AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等
11、7 12、35 13、4cm 14、16 15、12.6. 16、5cm. 17、10<x<22.
18、22.5cm,12.5cm,22.5cm,12.5cm.
三、解答题
19、【答案】详见解析
20、【答案】解:方法一:
补充条件①BE∥DF.
证明:如图,∵BE∥DF,
∴∠BEC=∠DFA,
∴∠BEA=∠DFC,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴四边形BFDE是平行四边形,
∴ED∥BF,
∴∠1=∠2;
方法二:
补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS),
∴∠1=∠2.
21、【答案】证明:由ABCD是平行四边形得AB∥CD,
∴∠CDE=∠F,∠C=∠EBF.
又∵E为BC的中点,
∴△DEC≌△FEB,
∴DC=FB.
又∵AB=CD,
∴AB=BF.
22、【答案】证明见解析.
根据两条对角线相互平分的四边形是平行四边形即可证明四边形AECF是平行四边形.
连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF为平行四边形.
23、【答案】本题是关于平行四边形的判定,判定方法有五种:?定义:两组对边分别平行的四边形是平行四边形;?两组对边分别相等的四边形是平行四边形?一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;⑤两组对角分别相等的四边形是平行四边形.找出合适的条件即可,此种类型题常有多种证法.举一证法如下:
试题解析:证明:∵BE⊥AD,BE⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,BE⊥AD,
∴BE∥CF
∴四边形BECF是平行四边形.
