2024-2025学年人教版九年级数学上册 期末巩固训练试卷(无答案)
文档属性
| 名称 | 2024-2025学年人教版九年级数学上册 期末巩固训练试卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 217.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 19:59:10 | ||
图片预览


文档简介
期末巩固训练2024-2025年度人教版九年级上册
选择题(每题3分,共30分)
1.观察下列图案,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.阳阳在解方程,只得一个解,阳阳漏掉的那个解是( )
A.x=3 B.x=1 C.x=0 D.x=2
3.从A,B,C三张卡片中任取两张,取到A,B的概率是( )
A. B. C. D.
4.已知四个二次函数的图象如图所示,那么的大小关系是( )
A. B.
C. D.
5.方程(x﹣2)(x﹣4)=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为( )
A.6 B.8 C.10 D.8或10
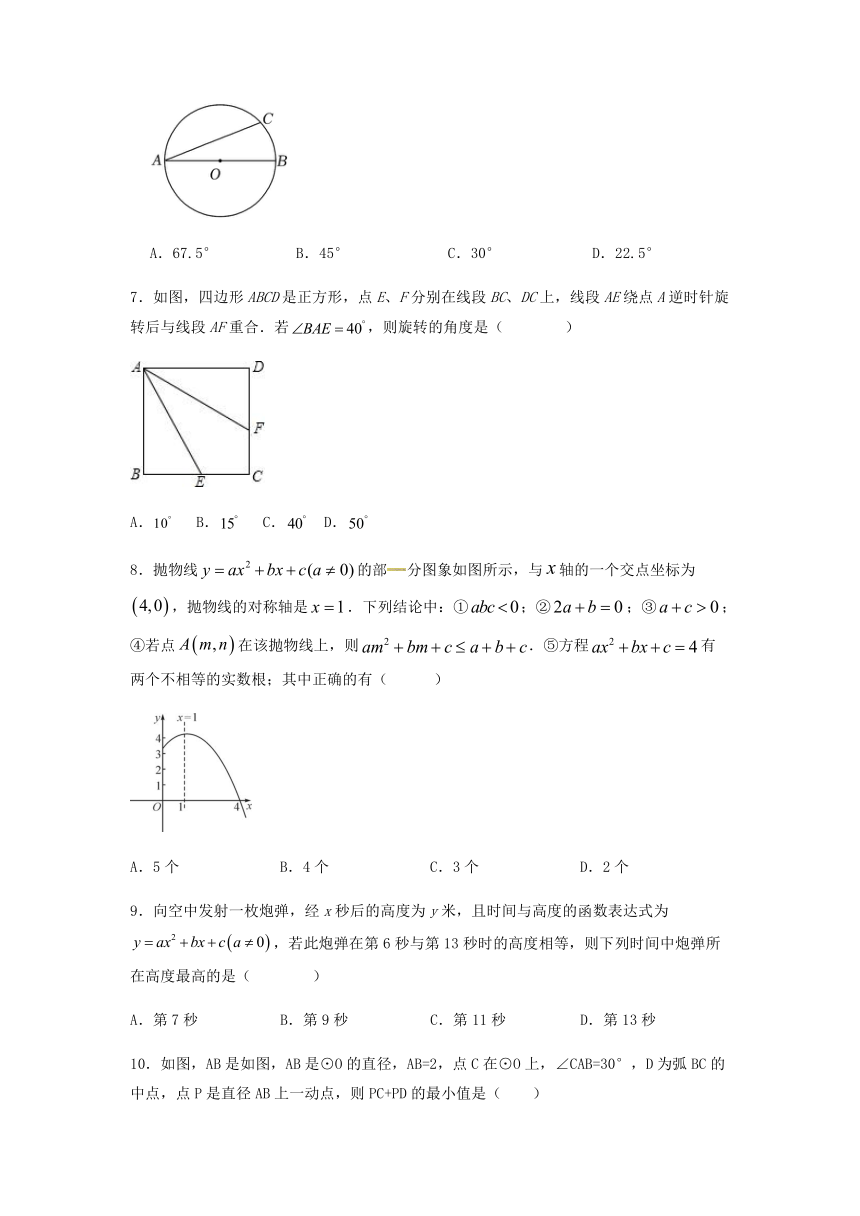
6.如图,AB是 O的直径,=3,则∠BAC=( )
A.67.5° B.45° C.30° D.22.5°
7.如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上,线段AE绕点A逆时针旋转后与线段AF重合.若,则旋转的角度是( )
A. B. C. D.
8.抛物线的部分图象如图所示,与轴的一个交点坐标为,抛物线的对称轴是.下列结论中:①;②;③;④若点在该抛物线上,则.⑤方程有两个不相等的实数根;其中正确的有( )
A.5个 B.4个 C.3个 D.2个
9.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的函数表达式为,若此炮弹在第6秒与第13秒时的高度相等,则下列时间中炮弹所在高度最高的是( )
A.第7秒 B.第9秒 C.第11秒 D.第13秒
10.如图,AB是如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,点P是直径AB上一动点,则PC+PD的最小值是( )
A.1 B. C. D.
二、填空题(每题3分,共18分)
11.把y=2x2﹣6x+4配方成y=a(x﹣h)2+k的形式是 .
12.关于x的一元二次方程x2+6x+m=0有两个相等的实数根,则m的值为 .
13.如图,点 是等边三角形 内一点,且 ,,,若将 绕着点 逆时针旋转后得到 ,则 的度数 .
14.如图,正方形的顶点在抛物线的第一象限的图象上,若点的横坐标与纵坐标之和等于6,则对角线的长为______.
15.有一个人患了流感,经过两轮传染后共有121人患了流感,设每轮平均一个人传染x个人,列方程得 ,因此每轮平均一个人传染了 个人.
16.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径,该圆锥的母线长,则扇形的圆心角度数为_______.
三、解答题(第17-19题每题6分,第20- 22题每题8分,第23题10分共52分)
17.用适当的方法解下列方程:
(1) . (2) .
18.根据“五项管理”文件精神,某学校优化学校作业管理,探索减负增效新举措,学校就学生做作业时间进行问卷调查,将收集信息进行统计分成A、B、C、D四个层级,其中A:90分钟以上;B:60~90分钟;C:30~60分钟;D:30分钟以下.并将结果绘制成两幅不完整的统计图,请你根据统计信息解答下列问题:
(1)接受问卷调查的学生共有____________人;
(2)求扇形统计图中“D”等级的扇形的圆心角的度数,并补全条形统计图;
(3)全校约有学生1500人,估计“A”层级的学生约有多少人?
(4)学校从“A”层级的的3名女生和2名男生中随机抽取2人参加现场深入调研,则恰好抽到1名男生和1名女生的概率是多少?
19.在平面直角坐标系中,已知三个顶点的坐标分别为,,.
(1)画出绕点A逆时针旋转90°后的,并写出点的坐标.
(2)求点C旋转到点所走的路径长.
20.“山竹”牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款1000元,第三天收到捐款1440元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到的捐款的增长速度,第四天该单位能收到多少捐款?
21.已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
22.如图,空地上有一段旧墙的长为20米,某人利用旧墙和木栏围成一个矩形菜园,已知木栏总长为100米.
(1)矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米,求所利用旧墙的长;
(2)请你设计一个方案,使得所围成的矩形菜园的面积最大,并求面积的最大值.
23.如图所示,抛物线y=x2+bx+c交x轴于A、B两点(点A在点B的左侧),交y轴于点C(0,﹣3),已知AB=4,对称轴在y轴左侧.
(1)求抛物线的表达式;
(2)若点N在对称轴上,则抛物线上是否存在点M,使得点A、O、N、M构成平行四边形,若存在,请求出点M的坐标;若不存在,请说明理由;
(3)若点P在抛物线上,且S△PBC=,请直接写出点P的坐标.
选择题(每题3分,共30分)
1.观察下列图案,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.阳阳在解方程,只得一个解,阳阳漏掉的那个解是( )
A.x=3 B.x=1 C.x=0 D.x=2
3.从A,B,C三张卡片中任取两张,取到A,B的概率是( )
A. B. C. D.
4.已知四个二次函数的图象如图所示,那么的大小关系是( )
A. B.
C. D.
5.方程(x﹣2)(x﹣4)=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为( )
A.6 B.8 C.10 D.8或10
6.如图,AB是 O的直径,=3,则∠BAC=( )
A.67.5° B.45° C.30° D.22.5°
7.如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上,线段AE绕点A逆时针旋转后与线段AF重合.若,则旋转的角度是( )
A. B. C. D.
8.抛物线的部分图象如图所示,与轴的一个交点坐标为,抛物线的对称轴是.下列结论中:①;②;③;④若点在该抛物线上,则.⑤方程有两个不相等的实数根;其中正确的有( )
A.5个 B.4个 C.3个 D.2个
9.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的函数表达式为,若此炮弹在第6秒与第13秒时的高度相等,则下列时间中炮弹所在高度最高的是( )
A.第7秒 B.第9秒 C.第11秒 D.第13秒
10.如图,AB是如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,点P是直径AB上一动点,则PC+PD的最小值是( )
A.1 B. C. D.
二、填空题(每题3分,共18分)
11.把y=2x2﹣6x+4配方成y=a(x﹣h)2+k的形式是 .
12.关于x的一元二次方程x2+6x+m=0有两个相等的实数根,则m的值为 .
13.如图,点 是等边三角形 内一点,且 ,,,若将 绕着点 逆时针旋转后得到 ,则 的度数 .
14.如图,正方形的顶点在抛物线的第一象限的图象上,若点的横坐标与纵坐标之和等于6,则对角线的长为______.
15.有一个人患了流感,经过两轮传染后共有121人患了流感,设每轮平均一个人传染x个人,列方程得 ,因此每轮平均一个人传染了 个人.
16.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径,该圆锥的母线长,则扇形的圆心角度数为_______.
三、解答题(第17-19题每题6分,第20- 22题每题8分,第23题10分共52分)
17.用适当的方法解下列方程:
(1) . (2) .
18.根据“五项管理”文件精神,某学校优化学校作业管理,探索减负增效新举措,学校就学生做作业时间进行问卷调查,将收集信息进行统计分成A、B、C、D四个层级,其中A:90分钟以上;B:60~90分钟;C:30~60分钟;D:30分钟以下.并将结果绘制成两幅不完整的统计图,请你根据统计信息解答下列问题:
(1)接受问卷调查的学生共有____________人;
(2)求扇形统计图中“D”等级的扇形的圆心角的度数,并补全条形统计图;
(3)全校约有学生1500人,估计“A”层级的学生约有多少人?
(4)学校从“A”层级的的3名女生和2名男生中随机抽取2人参加现场深入调研,则恰好抽到1名男生和1名女生的概率是多少?
19.在平面直角坐标系中,已知三个顶点的坐标分别为,,.
(1)画出绕点A逆时针旋转90°后的,并写出点的坐标.
(2)求点C旋转到点所走的路径长.
20.“山竹”牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款1000元,第三天收到捐款1440元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到的捐款的增长速度,第四天该单位能收到多少捐款?
21.已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
22.如图,空地上有一段旧墙的长为20米,某人利用旧墙和木栏围成一个矩形菜园,已知木栏总长为100米.
(1)矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米,求所利用旧墙的长;
(2)请你设计一个方案,使得所围成的矩形菜园的面积最大,并求面积的最大值.
23.如图所示,抛物线y=x2+bx+c交x轴于A、B两点(点A在点B的左侧),交y轴于点C(0,﹣3),已知AB=4,对称轴在y轴左侧.
(1)求抛物线的表达式;
(2)若点N在对称轴上,则抛物线上是否存在点M,使得点A、O、N、M构成平行四边形,若存在,请求出点M的坐标;若不存在,请说明理由;
(3)若点P在抛物线上,且S△PBC=,请直接写出点P的坐标.
同课章节目录
