期末热点复习 组成等腰三角形点的个数 (含详解)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 期末热点复习 组成等腰三角形点的个数 (含详解)2024-2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 450.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览



文档简介
期末热点复习 组成等腰三角形点的个数
【基础篇】
1.已知平面直角坐标系中有,两点.若在坐标轴上取点,使为等腰三角形,则满足条件的点的个数是( )
A.4 B.5 C.6 D.7
2.在直角坐标系中,为坐标原点,已知,在轴上确定点,使为等腰三角形,则符合条件的点共有 个.
3.如图,在中,,.点为直线上一动点,若点与三个顶点中的两个顶点构造成等腰三角形,那么满足条件的点的位置有( )
A.个 B.个 C.个 D.个
4.如图,在的网格中,每个网格线的交点称为格点.已知图中,两个格点,请在图中再寻找另一个格点,使成为等腰三角形,则满足条件的点有( )个.
A. B. C. D.
5.野营活动中,小明用一张等腰三角形的铁皮代替锅,烙一块与铁皮形状、大小相同的饼,烙好一面后把饼翻身,这块饼能正好落在“锅”中.小丽有四张三角形的铁皮(如图所示),她想选择其中的一张铁皮代替锅,烙一块与所选铁皮形状、大小相同的饼,烙好一面后,将饼切一刀,然后将两小块都翻身,饼也能正好落在“锅”中.她的选择最多有( )
A.1种 B.2种 C.3种 D.4种
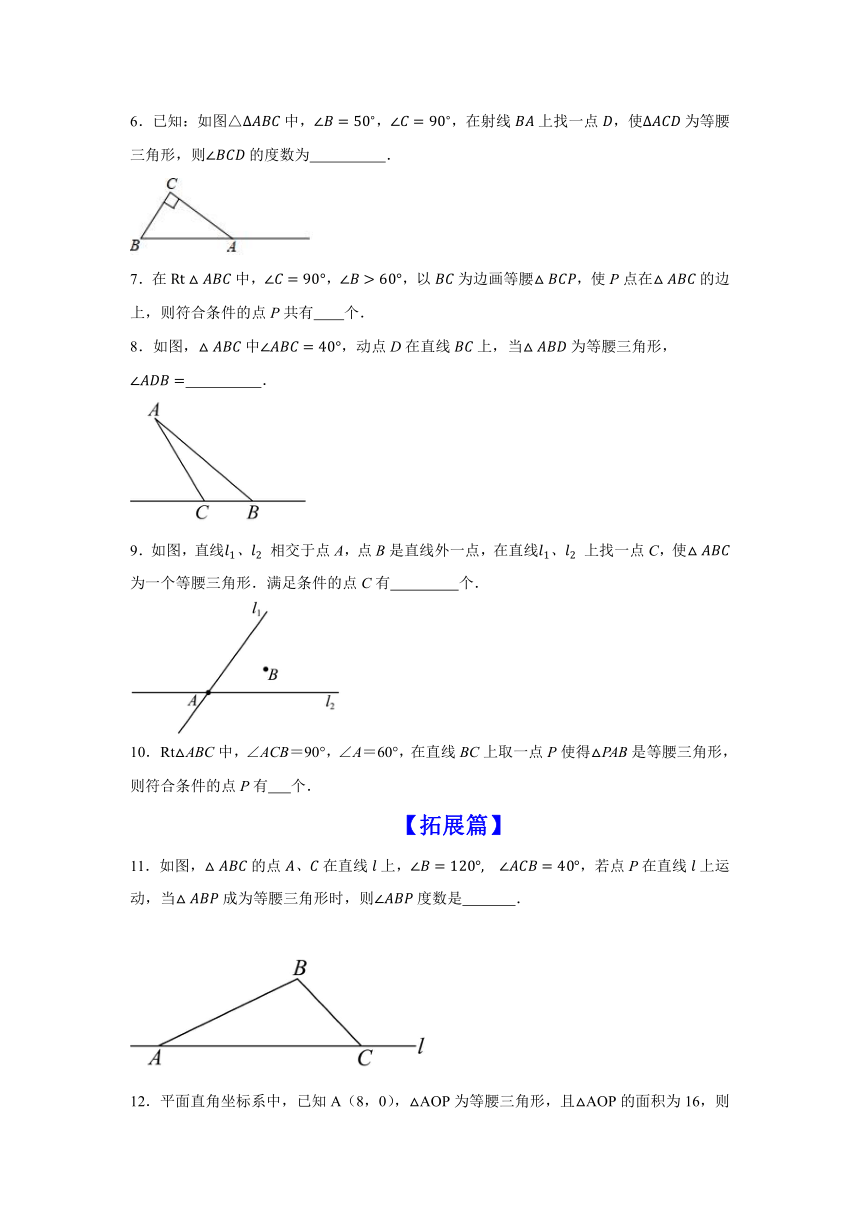
6.已知:如图△中,,,在射线上找一点,使为等腰三角形,则的度数为 .
7.在中,,,以为边画等腰,使P点在的边上,则符合条件的点P共有 个.
8.如图,中,动点D在直线上,当为等腰三角形, .
9.如图,直线 相交于点A,点B是直线外一点,在直线 上找一点C,使 为一个等腰三角形.满足条件的点C有 个.
Rt△ABC中,∠ACB=90°,∠A=60°,在直线BC上取一点P使得△PAB是等腰三角形,则符合条件的点P有 个.
【拓展篇】
11.如图,的点在直线上,,若点P在直线上运动,当成为等腰三角形时,则度数是 .
12.平面直角坐标系中,已知A(8,0),△AOP为等腰三角形,且△AOP的面积为16,则满足条件的P点个数是 .
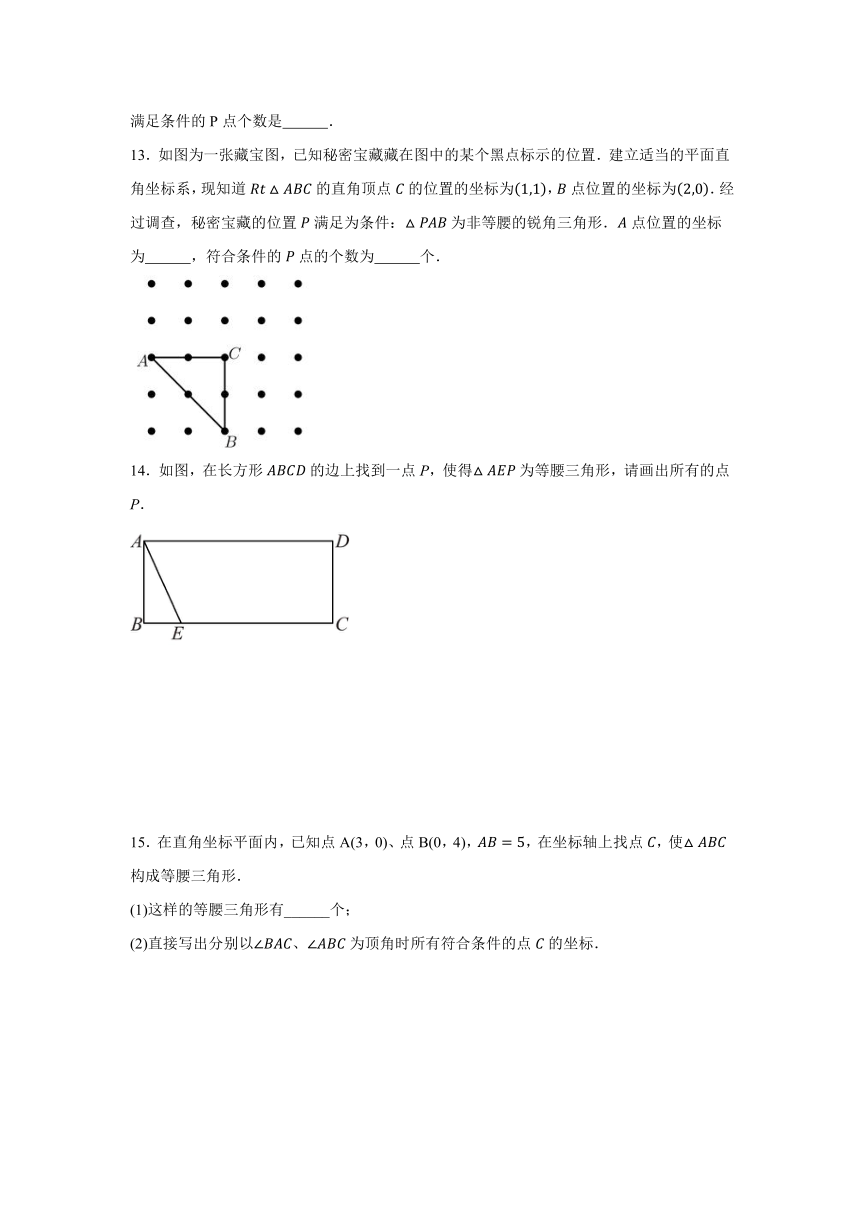
13.如图为一张藏宝图,已知秘密宝藏藏在图中的某个黑点标示的位置.建立适当的平面直角坐标系,现知道的直角顶点的位置的坐标为,点位置的坐标为.经过调查,秘密宝藏的位置满足为条件:为非等腰的锐角三角形.点位置的坐标为 ,符合条件的点的个数为 个.
14.如图,在长方形的边上找到一点P,使得为等腰三角形,请画出所有的点P.
15.在直角坐标平面内,已知点A(3,0)、点B(0,4),,在坐标轴上找点,使构成等腰三角形.
(1)这样的等腰三角形有______个;
(2)直接写出分别以、为顶角时所有符合条件的点的坐标.
参考答案:
1.B
【分析】本题考查了平面直角坐标系中点的坐标的特征,等腰三角形的定义,线段的垂直平分线的判定,利用圆的定义作图,掌握等腰三角形的作图是解题的关键.由题意知,是等腰三角形,故需分三种情况进行讨论,分别是,画出图形即可得到结论.
【详解】解:当,以为圆心,为半径作圆,与坐标轴有2个交点,但是点三点共线,故有1个等腰三角形,如图:
当时,以为圆心,为半径作圆,与坐标轴有2个交点,故有2个等腰三角形,如图:
当时,作出的垂直平分线,坐标轴有2个交点,故有2个等腰三角形,如图:
综上所述,共计有5个符合条件的点C,
故选:B.
2.4
【分析】本题考查了等腰三角形的性质,坐标与图形的性质,能正确进行分类求出所有的情况是解题的关键.有三种情况:当时,以为圆心,以为半径画圆,看与轴交点个数;当时,以为圆心,以为半径画圆,看与轴交点个数;当时,作的中垂线,看中垂线与轴的交点个数,从而得到答案.
【详解】解:如图,有三种情况
当时,以为圆心,以为半径的圆与轴交点有1个;
当时,以为圆心,以为半径的圆与轴交点有2个;
当时,作的中垂线,中垂线与轴的交点有1个.
故答案为:4.
3.C
【分析】本题考查等腰三角形的判定,根据等角对等边,从右到左依次考虑,即可得到所有构成等腰三角形的情况,得到满足条件的点的个数.熟练掌握等腰三角形的判定是解本题的关键.也考查了三角形内角和定理.
【详解】解:如图,
∵在中,,,
∴,
当时,为等腰三角形;
当时,为等腰三角形;
当时,为等腰三角形;
当与重合时,为等腰三角形;
当与重合时,为等腰三角形;
当时,为等腰三角形;
当时,为等腰三角形;
当时,为等腰三角形;
综上,满足条件的点的位置有个.
故选:C.
4.B
【分析】根据题意,分三种情况:当时,当时,当时,即可解答.
【详解】解:如图所示:
分三种情况:
①当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
②当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
③当时,作的垂直平分线,交网格线的格点为,,,,
综上所述:使成为等腰三角形,则满足条件的点有个,
故选:B.
【点睛】本题考查了等腰三角形的判定,根据题意,分三种情况讨论是解题的关键.
5.C
【分析】根据翻身后饼也能正好落在“锅”中,考虑把三角形分成两个等腰三角形即可.
【详解】解:如图,第一个沿直角三角形作斜边上的中线切,
第二个三角形在钝角处沿20°角的另一边切,
第三个三角形在60°角处沿20°角的另一边切,
第四个三角形无法分成两个等腰三角形,
所以,她的选择最多有3种.
故选C.
【点睛】本题考查了等腰三角形的性质,判断出翻折后正好能够重合是三角形是等腰三角形是解题的关键.
6.或50°或
【分析】分三种情形分别求解即可.
【详解】中,∵,,
∴∠BAC=40 ,
如图,为等腰三角形有三种情形:
①当时,
∵,∠BAC=40 ,
∴=,
∴=;
②当时,
,
∴;
③当时,
∵,∠BAC=40 ,
∴,
∴=;
故答案为:或50°或
【点睛】本题考查等腰三角形的判定,三角形的内角和定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
7.4
【分析】本题考查了等腰三角形的判定和性质,分三种情况:当时,当时,当时,掌握等腰三角形的判定和性质是解决问题的关键.
【详解】解:分三种情况:
当时,如图,以点为圆心,长为半径作弧,交,分别于点,;
当时,以点为圆心,长为半径作弧,交于点;
当时,作的垂直平分线交于点.
综上,符合条件的点共有4个,
故答案为:4
8.或或或
【分析】画出图形,分四种情况分别求解.
【详解】解:若,
则;
若,
则,
∴;
若,且三角形是锐角三角形,
则;
若,且三角形是钝角三角形,
则.
综上:的度数为或或或,
故答案为:或或或.
【点睛】本题考查了等腰三角形的性质,外角的性质,解题的关键是找齐所有情况,分类讨论.
9.8
【分析】分为两种情况:①以AB为底时,②以AB为腰时,想象画出图形,即可得出答案.
【详解】解:连接AB,
分为两种情况:
①以AB为底时,作AB的垂直平分线分别交两直线于一点,此时符合的有两个点 ;
②以AB为腰时,第一种情况:以B为圆心,以AB为半径画弧,与两直线的交点共2个(A点除外),
第二中情况:以A为圆心,以AB为半径画弧,与两直线的交点共4个,
即满足条件的有(个),
故答案为:8.
【点睛】本题考查了等腰三角形的判定的应用,分情况讨论才能做到不重不漏是解题的关键.
10.4
【分析】分别以A、B为圆心,以AB为半径作圆,再作AB的垂直平分线,即可得出答案.
【详解】解:以A为圆心,以AB为半径作圆,与直线BC有一个交点;
同理以B为圆心,以AB为半径作圆,与直线BC有两个交点;
作AB的垂直平分线与BC有一个交点,
即有1+2+1=4个,
故答案为4.
【点睛】本题考查了等腰三角形的判定和线段垂直平分线性质的应用,主要考查学生的理解能力和动手操作能力.
11.10°或80°或20°或140°
【分析】分三种情形:,,分别求解即可解决问题.
【详解】解:如图,
在中,,
①当时,,,
②当时,,
③当时,,
综上所述,满足条件的的值为或或或.
【点睛】本题考查等腰三角形的判定和性质,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于常考题型.
12.10
【分析】使△AOP为等腰三角形,只需分两种情况考虑:OA当底边或OA当腰.当OA是底边时,有2个点;当OA是腰时,有8个点,即可得出答案.
【详解】∵A(8,0),
∴OA=8,
设△AOP的边OA上的高是h,
则×8×h=16,
解得:h=4,
在x轴的两侧作直线a和直线b都和x轴平行,且到x轴的距离都等于4,如图:
①以A为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
②以O为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
③作AO的垂直平分线分别交直线a、b于一点,即共2个点符合,
其中,没有重复的点,
∴4+4+1+1=10.
故选:B.
【点睛】本题主要考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.
13. ; 4
【分析】根据已知点的坐标建立平面坐标系,即可得到点A的坐标,再根据等腰三角形的判定和锐角三角形的定义,结合图形即可得出结论.
【详解】解:∵为直角三角形,点坐标为,点坐标为,
∴所在直线为轴,垂直于所在直线为轴,如图所示:
∴点坐标为.
∵为非等腰的锐角三角形,
∴点不能在过点垂直于的直线上(不能等腰),
点不能在轴上(),不能在轴左侧(),
由对称性可知点不能在过点垂直于轴垂线上,以及右侧,下方那两点也不能(),
∴满足条件点,如图所示:,,,,共4个,
故答案为:(0,0);4.
【点睛】本题考查由点的坐标确定平面直角坐标系、等腰三角形、锐角三角形,理解等腰三角形和锐角三角形的定义,正确建立平面直角坐标系是解答的关键.
14.【分析】根据等腰三角形的定义找到符合题意的点.
【详解】解:如图,
AE=P1E,AP2=AE,AP3=EP3,AE=EP4,AP5=EP5,
则共有5个点P,使得△AEP为等腰三角形.
【点睛】此题主要考查了复杂作图以及等腰三角形的性质,利用分类讨论得出是解题关键.
15.(1)8
(2)当为顶角时,(8,0),(0,-4),(-2,0);当为顶角时,(-3,0),(0,-1),(0,9).
【分析】(1)分类讨论:①当AB=BC时,②当AB=AC时和③当BC=AC时,画出图形即可得出结论;
(2)根据(1)结合图形和等腰三角形的定义即可求解.
【详解】(1)分类讨论:①当AB=BC时,如图,和;
②当AB=AC时,如图,和;
③当BC=AC时,如图和.
综上可知满足条件的点C有个,
故答案为:;
(2)当为顶角时,即AB=AC=5,此时点C的位置即上图中,,.
∴,,,
∴(8,0),(0,-4),(-2,0);
当为顶角时,即AB=BC=5,此时点C的位置即上图中,,.
∴,,,
∴(-3,0),(0,-1),(0,9).
【点睛】本题考查坐标与图形,等腰三角形的定义.利用数形结合和分类讨论的思想是解题关键.
【基础篇】
1.已知平面直角坐标系中有,两点.若在坐标轴上取点,使为等腰三角形,则满足条件的点的个数是( )
A.4 B.5 C.6 D.7
2.在直角坐标系中,为坐标原点,已知,在轴上确定点,使为等腰三角形,则符合条件的点共有 个.
3.如图,在中,,.点为直线上一动点,若点与三个顶点中的两个顶点构造成等腰三角形,那么满足条件的点的位置有( )
A.个 B.个 C.个 D.个
4.如图,在的网格中,每个网格线的交点称为格点.已知图中,两个格点,请在图中再寻找另一个格点,使成为等腰三角形,则满足条件的点有( )个.
A. B. C. D.
5.野营活动中,小明用一张等腰三角形的铁皮代替锅,烙一块与铁皮形状、大小相同的饼,烙好一面后把饼翻身,这块饼能正好落在“锅”中.小丽有四张三角形的铁皮(如图所示),她想选择其中的一张铁皮代替锅,烙一块与所选铁皮形状、大小相同的饼,烙好一面后,将饼切一刀,然后将两小块都翻身,饼也能正好落在“锅”中.她的选择最多有( )
A.1种 B.2种 C.3种 D.4种
6.已知:如图△中,,,在射线上找一点,使为等腰三角形,则的度数为 .
7.在中,,,以为边画等腰,使P点在的边上,则符合条件的点P共有 个.
8.如图,中,动点D在直线上,当为等腰三角形, .
9.如图,直线 相交于点A,点B是直线外一点,在直线 上找一点C,使 为一个等腰三角形.满足条件的点C有 个.
Rt△ABC中,∠ACB=90°,∠A=60°,在直线BC上取一点P使得△PAB是等腰三角形,则符合条件的点P有 个.
【拓展篇】
11.如图,的点在直线上,,若点P在直线上运动,当成为等腰三角形时,则度数是 .
12.平面直角坐标系中,已知A(8,0),△AOP为等腰三角形,且△AOP的面积为16,则满足条件的P点个数是 .
13.如图为一张藏宝图,已知秘密宝藏藏在图中的某个黑点标示的位置.建立适当的平面直角坐标系,现知道的直角顶点的位置的坐标为,点位置的坐标为.经过调查,秘密宝藏的位置满足为条件:为非等腰的锐角三角形.点位置的坐标为 ,符合条件的点的个数为 个.
14.如图,在长方形的边上找到一点P,使得为等腰三角形,请画出所有的点P.
15.在直角坐标平面内,已知点A(3,0)、点B(0,4),,在坐标轴上找点,使构成等腰三角形.
(1)这样的等腰三角形有______个;
(2)直接写出分别以、为顶角时所有符合条件的点的坐标.
参考答案:
1.B
【分析】本题考查了平面直角坐标系中点的坐标的特征,等腰三角形的定义,线段的垂直平分线的判定,利用圆的定义作图,掌握等腰三角形的作图是解题的关键.由题意知,是等腰三角形,故需分三种情况进行讨论,分别是,画出图形即可得到结论.
【详解】解:当,以为圆心,为半径作圆,与坐标轴有2个交点,但是点三点共线,故有1个等腰三角形,如图:
当时,以为圆心,为半径作圆,与坐标轴有2个交点,故有2个等腰三角形,如图:
当时,作出的垂直平分线,坐标轴有2个交点,故有2个等腰三角形,如图:
综上所述,共计有5个符合条件的点C,
故选:B.
2.4
【分析】本题考查了等腰三角形的性质,坐标与图形的性质,能正确进行分类求出所有的情况是解题的关键.有三种情况:当时,以为圆心,以为半径画圆,看与轴交点个数;当时,以为圆心,以为半径画圆,看与轴交点个数;当时,作的中垂线,看中垂线与轴的交点个数,从而得到答案.
【详解】解:如图,有三种情况
当时,以为圆心,以为半径的圆与轴交点有1个;
当时,以为圆心,以为半径的圆与轴交点有2个;
当时,作的中垂线,中垂线与轴的交点有1个.
故答案为:4.
3.C
【分析】本题考查等腰三角形的判定,根据等角对等边,从右到左依次考虑,即可得到所有构成等腰三角形的情况,得到满足条件的点的个数.熟练掌握等腰三角形的判定是解本题的关键.也考查了三角形内角和定理.
【详解】解:如图,
∵在中,,,
∴,
当时,为等腰三角形;
当时,为等腰三角形;
当时,为等腰三角形;
当与重合时,为等腰三角形;
当与重合时,为等腰三角形;
当时,为等腰三角形;
当时,为等腰三角形;
当时,为等腰三角形;
综上,满足条件的点的位置有个.
故选:C.
4.B
【分析】根据题意,分三种情况:当时,当时,当时,即可解答.
【详解】解:如图所示:
分三种情况:
①当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
②当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
③当时,作的垂直平分线,交网格线的格点为,,,,
综上所述:使成为等腰三角形,则满足条件的点有个,
故选:B.
【点睛】本题考查了等腰三角形的判定,根据题意,分三种情况讨论是解题的关键.
5.C
【分析】根据翻身后饼也能正好落在“锅”中,考虑把三角形分成两个等腰三角形即可.
【详解】解:如图,第一个沿直角三角形作斜边上的中线切,
第二个三角形在钝角处沿20°角的另一边切,
第三个三角形在60°角处沿20°角的另一边切,
第四个三角形无法分成两个等腰三角形,
所以,她的选择最多有3种.
故选C.
【点睛】本题考查了等腰三角形的性质,判断出翻折后正好能够重合是三角形是等腰三角形是解题的关键.
6.或50°或
【分析】分三种情形分别求解即可.
【详解】中,∵,,
∴∠BAC=40 ,
如图,为等腰三角形有三种情形:
①当时,
∵,∠BAC=40 ,
∴=,
∴=;
②当时,
,
∴;
③当时,
∵,∠BAC=40 ,
∴,
∴=;
故答案为:或50°或
【点睛】本题考查等腰三角形的判定,三角形的内角和定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
7.4
【分析】本题考查了等腰三角形的判定和性质,分三种情况:当时,当时,当时,掌握等腰三角形的判定和性质是解决问题的关键.
【详解】解:分三种情况:
当时,如图,以点为圆心,长为半径作弧,交,分别于点,;
当时,以点为圆心,长为半径作弧,交于点;
当时,作的垂直平分线交于点.
综上,符合条件的点共有4个,
故答案为:4
8.或或或
【分析】画出图形,分四种情况分别求解.
【详解】解:若,
则;
若,
则,
∴;
若,且三角形是锐角三角形,
则;
若,且三角形是钝角三角形,
则.
综上:的度数为或或或,
故答案为:或或或.
【点睛】本题考查了等腰三角形的性质,外角的性质,解题的关键是找齐所有情况,分类讨论.
9.8
【分析】分为两种情况:①以AB为底时,②以AB为腰时,想象画出图形,即可得出答案.
【详解】解:连接AB,
分为两种情况:
①以AB为底时,作AB的垂直平分线分别交两直线于一点,此时符合的有两个点 ;
②以AB为腰时,第一种情况:以B为圆心,以AB为半径画弧,与两直线的交点共2个(A点除外),
第二中情况:以A为圆心,以AB为半径画弧,与两直线的交点共4个,
即满足条件的有(个),
故答案为:8.
【点睛】本题考查了等腰三角形的判定的应用,分情况讨论才能做到不重不漏是解题的关键.
10.4
【分析】分别以A、B为圆心,以AB为半径作圆,再作AB的垂直平分线,即可得出答案.
【详解】解:以A为圆心,以AB为半径作圆,与直线BC有一个交点;
同理以B为圆心,以AB为半径作圆,与直线BC有两个交点;
作AB的垂直平分线与BC有一个交点,
即有1+2+1=4个,
故答案为4.
【点睛】本题考查了等腰三角形的判定和线段垂直平分线性质的应用,主要考查学生的理解能力和动手操作能力.
11.10°或80°或20°或140°
【分析】分三种情形:,,分别求解即可解决问题.
【详解】解:如图,
在中,,
①当时,,,
②当时,,
③当时,,
综上所述,满足条件的的值为或或或.
【点睛】本题考查等腰三角形的判定和性质,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于常考题型.
12.10
【分析】使△AOP为等腰三角形,只需分两种情况考虑:OA当底边或OA当腰.当OA是底边时,有2个点;当OA是腰时,有8个点,即可得出答案.
【详解】∵A(8,0),
∴OA=8,
设△AOP的边OA上的高是h,
则×8×h=16,
解得:h=4,
在x轴的两侧作直线a和直线b都和x轴平行,且到x轴的距离都等于4,如图:
①以A为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
②以O为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
③作AO的垂直平分线分别交直线a、b于一点,即共2个点符合,
其中,没有重复的点,
∴4+4+1+1=10.
故选:B.
【点睛】本题主要考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.
13. ; 4
【分析】根据已知点的坐标建立平面坐标系,即可得到点A的坐标,再根据等腰三角形的判定和锐角三角形的定义,结合图形即可得出结论.
【详解】解:∵为直角三角形,点坐标为,点坐标为,
∴所在直线为轴,垂直于所在直线为轴,如图所示:
∴点坐标为.
∵为非等腰的锐角三角形,
∴点不能在过点垂直于的直线上(不能等腰),
点不能在轴上(),不能在轴左侧(),
由对称性可知点不能在过点垂直于轴垂线上,以及右侧,下方那两点也不能(),
∴满足条件点,如图所示:,,,,共4个,
故答案为:(0,0);4.
【点睛】本题考查由点的坐标确定平面直角坐标系、等腰三角形、锐角三角形,理解等腰三角形和锐角三角形的定义,正确建立平面直角坐标系是解答的关键.
14.【分析】根据等腰三角形的定义找到符合题意的点.
【详解】解:如图,
AE=P1E,AP2=AE,AP3=EP3,AE=EP4,AP5=EP5,
则共有5个点P,使得△AEP为等腰三角形.
【点睛】此题主要考查了复杂作图以及等腰三角形的性质,利用分类讨论得出是解题关键.
15.(1)8
(2)当为顶角时,(8,0),(0,-4),(-2,0);当为顶角时,(-3,0),(0,-1),(0,9).
【分析】(1)分类讨论:①当AB=BC时,②当AB=AC时和③当BC=AC时,画出图形即可得出结论;
(2)根据(1)结合图形和等腰三角形的定义即可求解.
【详解】(1)分类讨论:①当AB=BC时,如图,和;
②当AB=AC时,如图,和;
③当BC=AC时,如图和.
综上可知满足条件的点C有个,
故答案为:;
(2)当为顶角时,即AB=AC=5,此时点C的位置即上图中,,.
∴,,,
∴(8,0),(0,-4),(-2,0);
当为顶角时,即AB=BC=5,此时点C的位置即上图中,,.
∴,,,
∴(-3,0),(0,-1),(0,9).
【点睛】本题考查坐标与图形,等腰三角形的定义.利用数形结合和分类讨论的思想是解题关键.
同课章节目录
