15.2.3整数指数幂 课件(共22张PPT)
文档属性
| 名称 | 15.2.3整数指数幂 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 19:18:53 | ||
图片预览




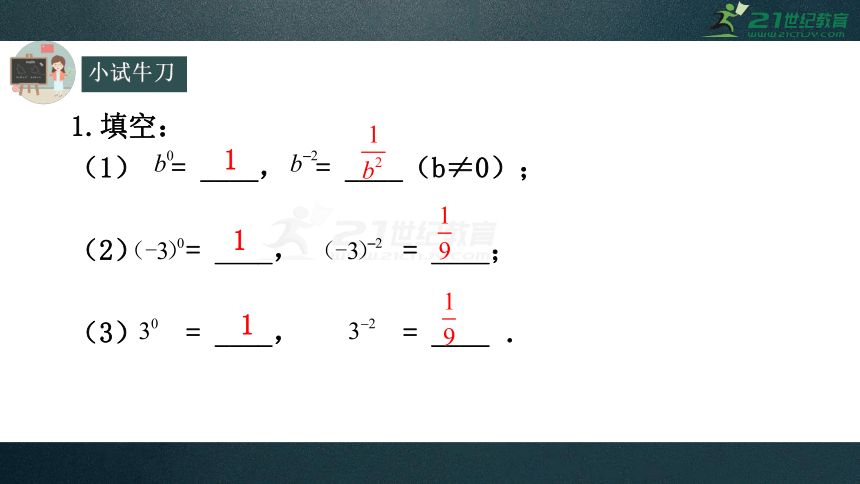


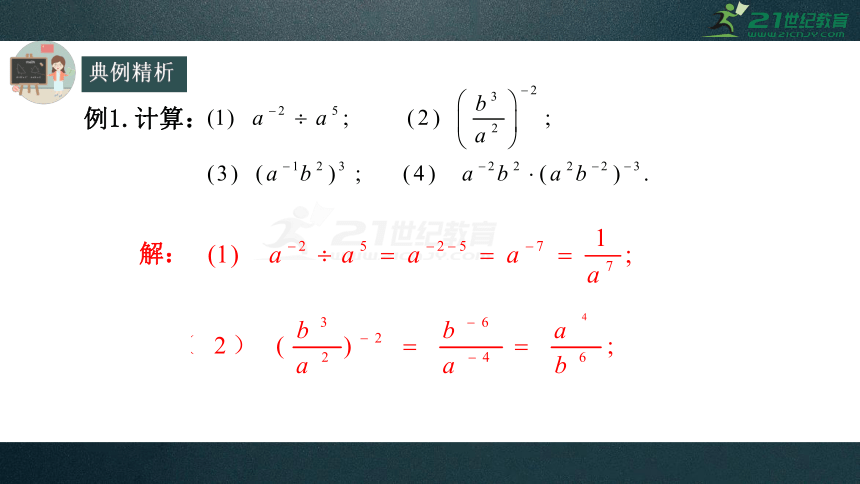
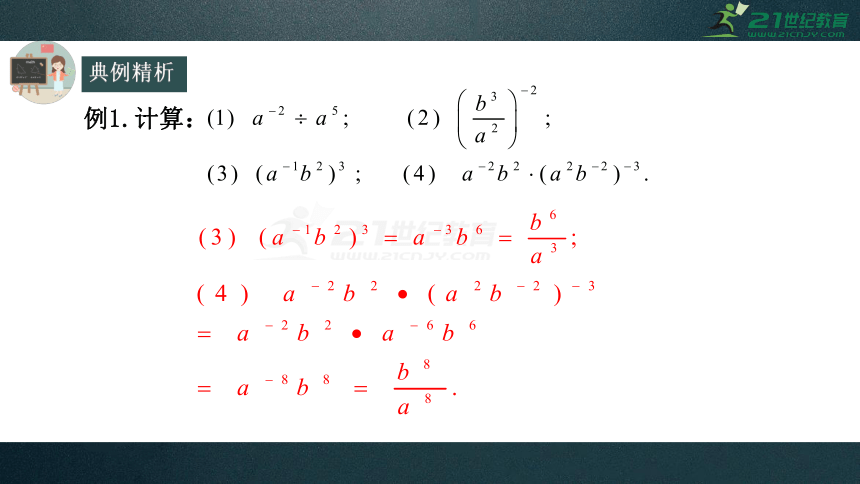
文档简介
(共22张PPT)
人教版 八年级数学上
15.2.3整数指数幂
教学目标
1.理解并掌握整数指数幂的运算性质.(重点)
2.会用科学记数法表示绝对值小于1的数.(重点)
3.理解负整数指数幂的性质并应用其解决实际问题.(难点)
温故知新
1.当n为正整数时,
2.正整数指数幂的运算性质:
0指数幂:
an中指数n可以是负整数吗?如果可以,那么负整数指数幂an表示什么?下面我们一起探究!
合作探究
计算:
根据分式的约分,得:
根据正整数指数幂的运算性质,得:
数学中规定:当n为正整数时,
即:a-n(a≠0)是an的倒数.
你现在能说出当m分别为正整数、0、负整数时,am各表示什么意思吗?
小试牛刀
1
1
1
1.填空:
(1) = ____, = ____(b≠0);
(2) = ____, = ____;
(3) = ____, = ____ .
合作探究
这条性质能否推广到m,n 是任意整数的情形?
思考:引入负整数指数和0指数后, (m,n 是
正整数)
即:
即:
即:
试一试:负整数指数幂或0指数幂对于其他正整数指数幂的运算性质是否符合?实验证明。
合作探究
整数指数幂的运算性质:
典例精析
例1.计算:
解:
典例精析
例1.计算:
合作探究
思考:通过以上实验,能否将整数指数幂的前5条性质进行适当合并?
同底数幂的除法转化为同底数幂的乘法.
商的乘方可以转化为积的乘方.
根据整数指数幂的运算性质,当m,n为整数时,
合作探究
这样,整数指数幂的运算性质可以归结为:
小试牛刀
1.计算: (1)x2y-3·(x-1y)3; (2)(2ab2c-3)-2÷(a-2b)3;
解:(1)原式=x2y-3·x-3y3
(2)原式=2-2a-2b-4c6÷(a-6b3)
醍醐灌顶:计算结果一般需化为正整数幂的形式.
=x-1
=2-2a4b-7c6
合作探究
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,
n是正整数.
忆一忆:
例如,696000可以写成 .
怎样把0.0000696用科学记数法表示?
6.96×105
想一想:
合作探究
0.1=
0.01=
0.001= = ;
0.000 1= = ;
0.000 01= = .
归纳:0.000···0001=
探索:
所以, 0.0000696=6.96 ×0.00001=6.96 ×10-5.
n个0
n个0
归纳:对于一个小于1的正小数,从左往右数至第一个非0数字
前有几个0,用科学计数法表示这个数时,10的指数就是负几。
这样,我们可以利用10的负整数次幂,用科学记数法表示一些小于1的正小数,即将它们表示成a×10- n的形式,其中n是正整数,1≤a<10.
小试牛刀
解:(1)0.00000000=1×10-9 ; (2)0.0012=1.2×10-3 ;
(3)0.000 000 345=3.45×10-7;
(4)0.000 000 010 8=1.08×10-8
1.用科学记数法表示下列各数:
(1)0.000 000 001;
(2)0.0012;
(3)0.000 000 345;
(4)0.000 000 010 8.
2.计算:(1)(2×10-6)×(3.2×103);
(2)(2×10-6)2÷(10-4)3.
(2)原式=4
解:(1)原式=6.4×10-3
小试牛刀
典例精析
例2.纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓
球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个
1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
实战演练
1.用小数表示下列各数:
(1)3×10-7;(2)3.14×10-5;
(3)7.06×10-4;(4)5.17×10-1.
解:(1)3×10-7=0.0000006;
(2)3.14×10-5=0.0000314;
(3)7.06×10-3=0.00706;
(4)5.17×10-1=0.517.
实战演练
2.下列是用科学记数法表示的数,写出原来的数.
(1)6×10-8 (2)2.005×10-6
解:(1)0.000 000 06 (2)0.000 002 005
3.计算:
(1)x4y-3(x-1y)3 (2)(2ab4c2)2÷(a3b)-3
解:(1)x (2)4a11b11c4
课堂小结
今天我们收获了哪些知识?
1.说一说正整数指数幂、负整数指数幂、0次幂分别表示什么含义? 2.如何用科学记数法表示小于1的正小数?
课后作业
教材146页习题15.2第7、8、9题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
15.2.3整数指数幂
教学目标
1.理解并掌握整数指数幂的运算性质.(重点)
2.会用科学记数法表示绝对值小于1的数.(重点)
3.理解负整数指数幂的性质并应用其解决实际问题.(难点)
温故知新
1.当n为正整数时,
2.正整数指数幂的运算性质:
0指数幂:
an中指数n可以是负整数吗?如果可以,那么负整数指数幂an表示什么?下面我们一起探究!
合作探究
计算:
根据分式的约分,得:
根据正整数指数幂的运算性质,得:
数学中规定:当n为正整数时,
即:a-n(a≠0)是an的倒数.
你现在能说出当m分别为正整数、0、负整数时,am各表示什么意思吗?
小试牛刀
1
1
1
1.填空:
(1) = ____, = ____(b≠0);
(2) = ____, = ____;
(3) = ____, = ____ .
合作探究
这条性质能否推广到m,n 是任意整数的情形?
思考:引入负整数指数和0指数后, (m,n 是
正整数)
即:
即:
即:
试一试:负整数指数幂或0指数幂对于其他正整数指数幂的运算性质是否符合?实验证明。
合作探究
整数指数幂的运算性质:
典例精析
例1.计算:
解:
典例精析
例1.计算:
合作探究
思考:通过以上实验,能否将整数指数幂的前5条性质进行适当合并?
同底数幂的除法转化为同底数幂的乘法.
商的乘方可以转化为积的乘方.
根据整数指数幂的运算性质,当m,n为整数时,
合作探究
这样,整数指数幂的运算性质可以归结为:
小试牛刀
1.计算: (1)x2y-3·(x-1y)3; (2)(2ab2c-3)-2÷(a-2b)3;
解:(1)原式=x2y-3·x-3y3
(2)原式=2-2a-2b-4c6÷(a-6b3)
醍醐灌顶:计算结果一般需化为正整数幂的形式.
=x-1
=2-2a4b-7c6
合作探究
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,
n是正整数.
忆一忆:
例如,696000可以写成 .
怎样把0.0000696用科学记数法表示?
6.96×105
想一想:
合作探究
0.1=
0.01=
0.001= = ;
0.000 1= = ;
0.000 01= = .
归纳:0.000···0001=
探索:
所以, 0.0000696=6.96 ×0.00001=6.96 ×10-5.
n个0
n个0
归纳:对于一个小于1的正小数,从左往右数至第一个非0数字
前有几个0,用科学计数法表示这个数时,10的指数就是负几。
这样,我们可以利用10的负整数次幂,用科学记数法表示一些小于1的正小数,即将它们表示成a×10- n的形式,其中n是正整数,1≤a<10.
小试牛刀
解:(1)0.00000000=1×10-9 ; (2)0.0012=1.2×10-3 ;
(3)0.000 000 345=3.45×10-7;
(4)0.000 000 010 8=1.08×10-8
1.用科学记数法表示下列各数:
(1)0.000 000 001;
(2)0.0012;
(3)0.000 000 345;
(4)0.000 000 010 8.
2.计算:(1)(2×10-6)×(3.2×103);
(2)(2×10-6)2÷(10-4)3.
(2)原式=4
解:(1)原式=6.4×10-3
小试牛刀
典例精析
例2.纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓
球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个
1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
实战演练
1.用小数表示下列各数:
(1)3×10-7;(2)3.14×10-5;
(3)7.06×10-4;(4)5.17×10-1.
解:(1)3×10-7=0.0000006;
(2)3.14×10-5=0.0000314;
(3)7.06×10-3=0.00706;
(4)5.17×10-1=0.517.
实战演练
2.下列是用科学记数法表示的数,写出原来的数.
(1)6×10-8 (2)2.005×10-6
解:(1)0.000 000 06 (2)0.000 002 005
3.计算:
(1)x4y-3(x-1y)3 (2)(2ab4c2)2÷(a3b)-3
解:(1)x (2)4a11b11c4
课堂小结
今天我们收获了哪些知识?
1.说一说正整数指数幂、负整数指数幂、0次幂分别表示什么含义? 2.如何用科学记数法表示小于1的正小数?
课后作业
教材146页习题15.2第7、8、9题.
https://www.21cnjy.com/help/help_extract.php
