期末优化练 2024--2025学年初中数学人教版八年级上册
文档属性
| 名称 | 期末优化练 2024--2025学年初中数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 09:31:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末优化练 2024--2025学年
初中数学人教版八年级上册
一、单选题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.下列计算中正确的是( )
A. B.
C. D.
3.要使分式有意义,则的取值应满足( )
A. B. C. D.
4.有一块三角形玻璃在运输过程中,不小心碎成如图所示的四块,嘉淇想按原来的大小在玻璃店再订制一块,需要带的两块可以是( )
A.①② B.②③ C.②④ D.①④
5.已知三角形的三边长分别是4,8,,则的取值可能是( )
A.10 B.11 C.12 D.13
6.下列因式分解不正确的是( )
A. B.
C. D.
7.如图,中,,根据尺规作图的痕迹判断以下结论错误的是( )
A. B. C. D.
8.已知,,则( )
A. B. C. D.
9.如图,在中,,点D在外,连接,,若,则的度数是( )
A. B. C. D.
10.如图,中,,的角平分线、相交于点,过作交的延长线于点,交于点,则下列结论:①;②;③;④,其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
11.若正边形的每一个内角为,则 .
12.分解因式: .
13.如果,则的值为 .
14.若是关于的完全平方式,则 .
15.若分式的值是零,则的值为 .
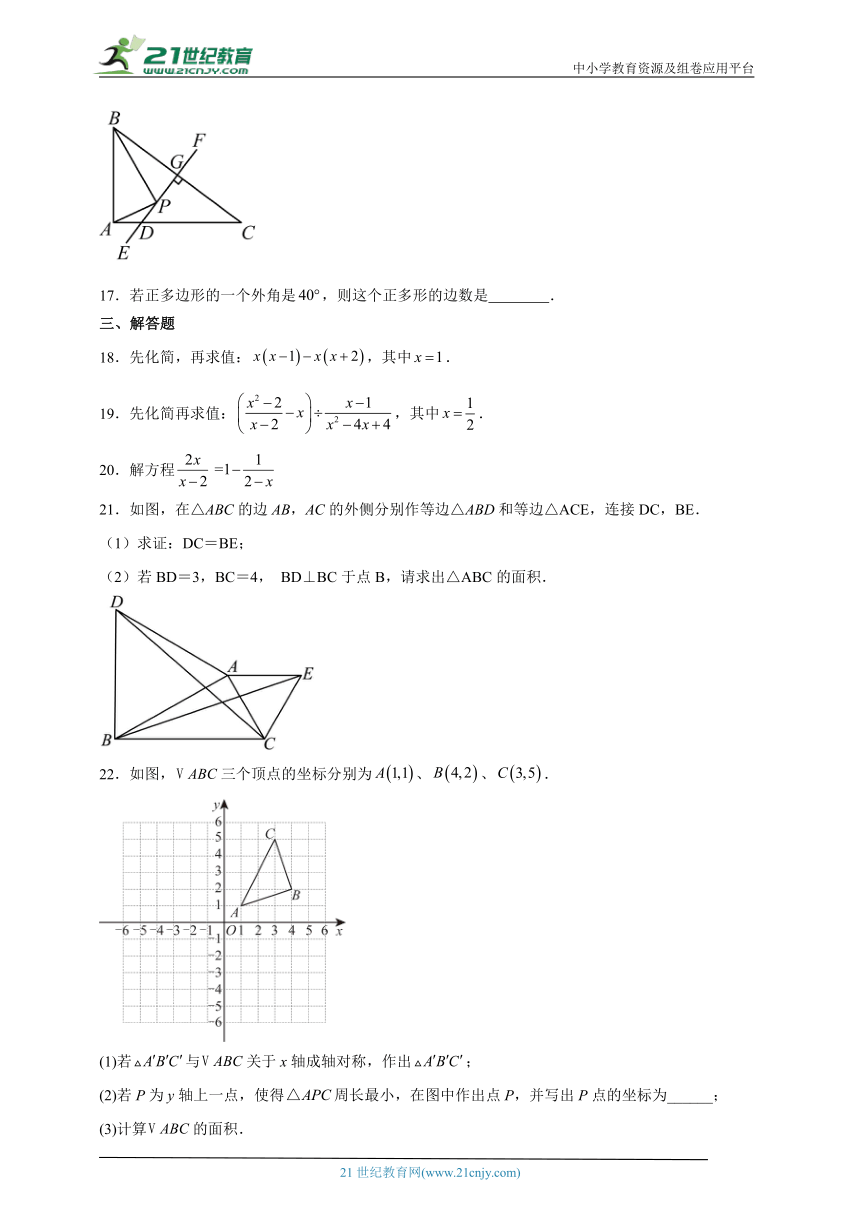
16.如图,在中,,垂直平分,交于点G,交于点D,P为直线上一动点(不在的延长线上),连接,则周长的最小值是 .
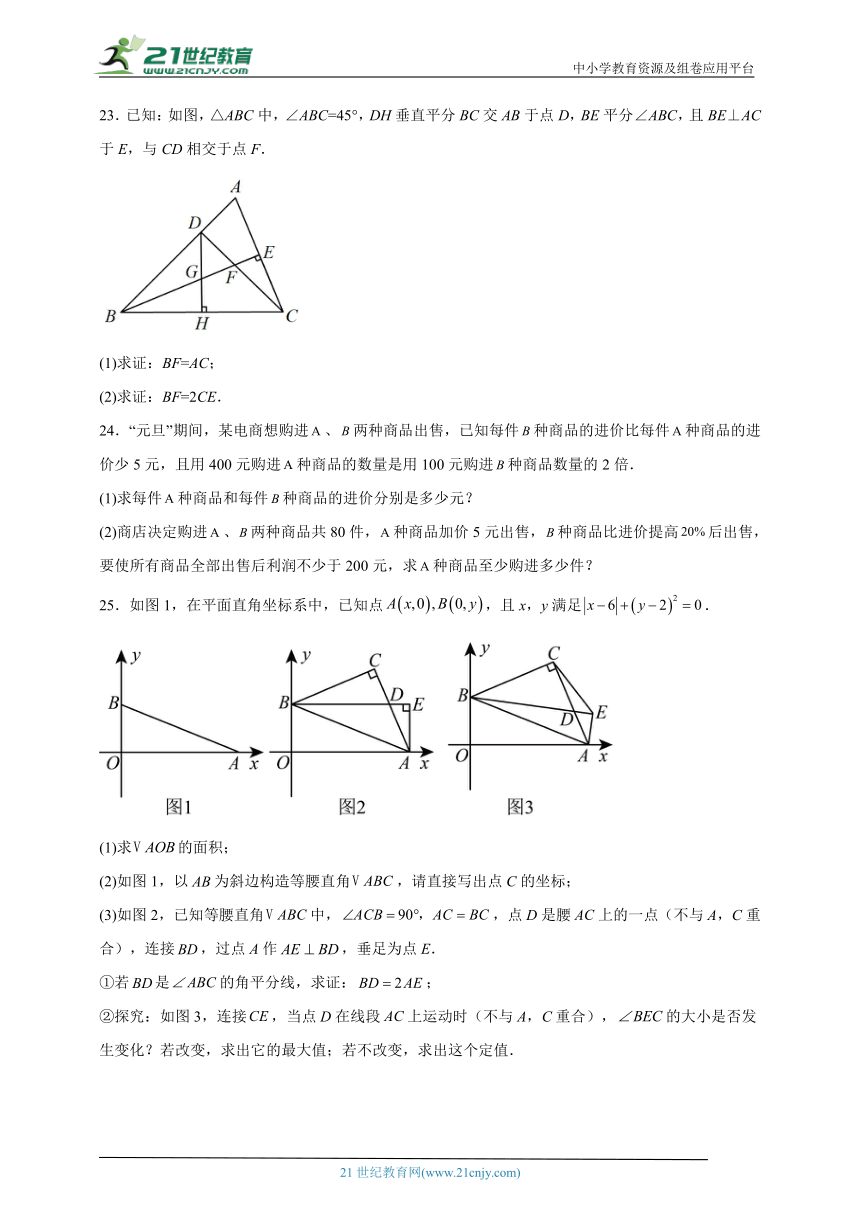
17.若正多边形的一个外角是,则这个正多形的边数是 .
三、解答题
18.先化简,再求值:,其中.
19.先化简再求值:,其中.
20.解方程
21.如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.
22.如图,三个顶点的坐标分别为、、.
(1)若与关于x轴成轴对称,作出;
(2)若P为y轴上一点,使得周长最小,在图中作出点P,并写出P点的坐标为______;
(3)计算的面积.
23.已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.
(1)求证:BF=AC;
(2)求证:BF=2CE.
24.“元旦”期间,某电商想购进、两种商品出售,已知每件种商品的进价比每件种商品的进价少5元,且用400元购进种商品的数量是用100元购进种商品数量的2倍.
(1)求每件种商品和每件种商品的进价分别是多少元?
(2)商店决定购进、两种商品共80件,种商品加价5元出售,种商品比进价提高后出售,要使所有商品全部出售后利润不少于200元,求种商品至少购进多少件?
25.如图1,在平面直角坐标系中,已知点,且x,y满足.
(1)求的面积;
(2)如图1,以为斜边构造等腰直角,请直接写出点C的坐标;
(3)如图2,已知等腰直角中,,点D是腰上的一点(不与A,C重合),连接,过点A作,垂足为点E.
①若是的角平分线,求证:;
②探究:如图3,连接,当点D在线段上运动时(不与A,C重合),的大小是否发生变化?若改变,求出它的最大值;若不改变,求出这个定值.
参考答案:
1.D
解:A,B,C三个选项中的图形都能找到一条直线,使图形对折后能够完全重合,是轴对称图形,不符合题意;
D选项的图形找不到一条直线,使图形对折后能够完全重合,不是轴对称图形,符合题意.
2.C
解:A.,原计算错误,不符合题意;
B.,原计算错误,不符合题意;
C.,原计算正确,符合题意;
D.,原计算错误,不符合题意;
3.D
解:根据题意得:,
,
4.D
解:想按原来的大小在玻璃店再订制一块,需要带的两块可以是①④或③④,
满足的为①④,
5.A
解:根据三角形三边关系可得:
解得:
6.D
解:A、,故不符合题意;
B、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
7.D
解:由尺规作图可知,AD是∠CAB角平分线,DE⊥AC,
在△AED和△ABD中:
∵,∴△AED≌△ABD(AAS),
∴DB=DE,AB=AE,选项A、B都正确,
又在Rt△EDC中,∠EDC=90°-∠C,
在Rt△ABC中,∠BAC=90°-∠C,
∴∠EDC=∠BAC,选项C正确,
选项D,题目中缺少条件证明,故选项D错误.
8.A
解:由题意得
;
9.C
解:如图,以为边,在内作,连接.
∵,
∴.
在中,
∵,
∴.
∴.
∵,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∵,
∴是等边三角形.
∴.
∴.
∵.
∴.
∴.
∵,
∴.
∴.
10.D
解:在中,,
,
又、分别平分、,
,
,故①正确;
,
又,
,
,
在和中,
,
,
,,,故②正确;
,
在和中,
,
,
,
又,
,故③正确;
连接,,如图所示:
,,
,,,
,
,
,
,
,故④正确,
11.10
解:正边形的每一个内角为,
则正边形的内角和为,
,
整理得,
解得.
故答案为:10.
12./
解:
=2(m2-9)
=2(m+3)(m-3).
故答案为:2(m+3)(m-3).
13.7
解:∵,
∴,
∴,
∴.
故答案为7.
14.7或-1
解:∵x2+2(m-3)x+16是关于x的完全平方式,
∴2(m-3)=±8,
解得:m=-1或7,
故答案为-1或7.
15.
解:由题得且,
解得:,
故答案为:.
16.14
解:∵垂直平分,
∴,
∴的周长=,
故答案为14.
17.九/9
解:,
∴这个多边形的边上是九.
故答案为:九.
18.
解:,
将代入得,原式.
19.,
解:
.
当时,原式.
20.x=-1.
解:方程两边同乘x-2,得2x=x-2+1
解这个方程,得x= -1
检验:x= -1时,x-2≠0
∴原方程的解是x= -1
21.(1)见解析(2)3
(1)证明: ∵等边△ABD和等边△ACE
∴AD=AB,AE=AC,∠DAB=∠EAC=60°
∴∠DAC=∠EAB
∴△DAC ≌△BAE
∴DC=BE
(2) 过点A作AH⊥BC于H
∵BD⊥BC
∴∠DBC=90°
∵等边△ABD
∴∠DBA=60° ,AB=BD=3
∴∠ABC=30°
∵AH⊥BC
∴AH= =
∴△ABC的面积=
22.(1)见解析
(2)见解析,
(3)5
(1)解:如图,即为所求;
(2)解:如图,点P即为所求.P坐标为,
故答案为.
(3)解:.
23.(1)见解析
(2)见解析
(1)证明:(1)∵DH垂直平分BC,且∠ABC=45°,
∴BD=DC,且∠BDC=90°,
∵∠A+∠ABF=90°,∠A+∠ACD=90°,
∴∠ABF=∠ACD,
在△BDF和△CDA中,
∴△BDF≌△CDA(ASA),
∴BF=AC.
(2)由(1)得BF=AC,
∵BE平分∠ABC,且BE⊥AC,
在△ABE和△CBE中,
∴△ABE≌△CBE(ASA),
∴.
∴BF=2CE.
24.(1)每件商品的进价为10元,每件商品的进价为5元
(2)种商品至少购进30件
(1)解:设每件商品的进价为元,则每件商品的进价为元,
根据题意,得,
解这个方程,得,
经检验,是原分式方程的解,且符合题意,
则,
答:每件商品的进价为10元,每件商品的进价为5元;
(2)解:设购进商品件,则购进商品件,
由题意,可得 ,
解得 ,
答:种商品至少购进30件.
25.(1)6
(2)或
(3)①证明见解析②的大小不变,总为,理由见解析
(1)解:,
,,
解得:,.
,,
的面积.
(2)当点C在上方时:
作为等腰直角三角形,过点作轴于F,轴于E,如图:
∴,
∵,
,,
,,
,
在和中,
,
,
,,
∵,
,即:,
解得:,
,,
;
当点C在下方时;
作为等腰直角三角形,过点作轴于F,轴于E,如图:
,,
,,
,
在和中,
,
,
,,
∵,
,
,即:,
解得:,
,
,
综上所述:点的坐标为:或.
(3)①延长,,它们相交于点,如图:
等腰直角中,,,且,
,
又,
,
在和中,
,
,
.
是的角平分线,
,
,
,
在和中,
,
,
即,
.
②的大小不变,总为,理由如下:
作,,垂足分别是,,如图:
,
由①可知:,,
在和中,
,
,
,
是的角平分线,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末优化练 2024--2025学年
初中数学人教版八年级上册
一、单选题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.下列计算中正确的是( )
A. B.
C. D.
3.要使分式有意义,则的取值应满足( )
A. B. C. D.
4.有一块三角形玻璃在运输过程中,不小心碎成如图所示的四块,嘉淇想按原来的大小在玻璃店再订制一块,需要带的两块可以是( )
A.①② B.②③ C.②④ D.①④
5.已知三角形的三边长分别是4,8,,则的取值可能是( )
A.10 B.11 C.12 D.13
6.下列因式分解不正确的是( )
A. B.
C. D.
7.如图,中,,根据尺规作图的痕迹判断以下结论错误的是( )
A. B. C. D.
8.已知,,则( )
A. B. C. D.
9.如图,在中,,点D在外,连接,,若,则的度数是( )
A. B. C. D.
10.如图,中,,的角平分线、相交于点,过作交的延长线于点,交于点,则下列结论:①;②;③;④,其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
11.若正边形的每一个内角为,则 .
12.分解因式: .
13.如果,则的值为 .
14.若是关于的完全平方式,则 .
15.若分式的值是零,则的值为 .
16.如图,在中,,垂直平分,交于点G,交于点D,P为直线上一动点(不在的延长线上),连接,则周长的最小值是 .
17.若正多边形的一个外角是,则这个正多形的边数是 .
三、解答题
18.先化简,再求值:,其中.
19.先化简再求值:,其中.
20.解方程
21.如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.
22.如图,三个顶点的坐标分别为、、.
(1)若与关于x轴成轴对称,作出;
(2)若P为y轴上一点,使得周长最小,在图中作出点P,并写出P点的坐标为______;
(3)计算的面积.
23.已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.
(1)求证:BF=AC;
(2)求证:BF=2CE.
24.“元旦”期间,某电商想购进、两种商品出售,已知每件种商品的进价比每件种商品的进价少5元,且用400元购进种商品的数量是用100元购进种商品数量的2倍.
(1)求每件种商品和每件种商品的进价分别是多少元?
(2)商店决定购进、两种商品共80件,种商品加价5元出售,种商品比进价提高后出售,要使所有商品全部出售后利润不少于200元,求种商品至少购进多少件?
25.如图1,在平面直角坐标系中,已知点,且x,y满足.
(1)求的面积;
(2)如图1,以为斜边构造等腰直角,请直接写出点C的坐标;
(3)如图2,已知等腰直角中,,点D是腰上的一点(不与A,C重合),连接,过点A作,垂足为点E.
①若是的角平分线,求证:;
②探究:如图3,连接,当点D在线段上运动时(不与A,C重合),的大小是否发生变化?若改变,求出它的最大值;若不改变,求出这个定值.
参考答案:
1.D
解:A,B,C三个选项中的图形都能找到一条直线,使图形对折后能够完全重合,是轴对称图形,不符合题意;
D选项的图形找不到一条直线,使图形对折后能够完全重合,不是轴对称图形,符合题意.
2.C
解:A.,原计算错误,不符合题意;
B.,原计算错误,不符合题意;
C.,原计算正确,符合题意;
D.,原计算错误,不符合题意;
3.D
解:根据题意得:,
,
4.D
解:想按原来的大小在玻璃店再订制一块,需要带的两块可以是①④或③④,
满足的为①④,
5.A
解:根据三角形三边关系可得:
解得:
6.D
解:A、,故不符合题意;
B、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
7.D
解:由尺规作图可知,AD是∠CAB角平分线,DE⊥AC,
在△AED和△ABD中:
∵,∴△AED≌△ABD(AAS),
∴DB=DE,AB=AE,选项A、B都正确,
又在Rt△EDC中,∠EDC=90°-∠C,
在Rt△ABC中,∠BAC=90°-∠C,
∴∠EDC=∠BAC,选项C正确,
选项D,题目中缺少条件证明,故选项D错误.
8.A
解:由题意得
;
9.C
解:如图,以为边,在内作,连接.
∵,
∴.
在中,
∵,
∴.
∴.
∵,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∵,
∴是等边三角形.
∴.
∴.
∵.
∴.
∴.
∵,
∴.
∴.
10.D
解:在中,,
,
又、分别平分、,
,
,故①正确;
,
又,
,
,
在和中,
,
,
,,,故②正确;
,
在和中,
,
,
,
又,
,故③正确;
连接,,如图所示:
,,
,,,
,
,
,
,
,故④正确,
11.10
解:正边形的每一个内角为,
则正边形的内角和为,
,
整理得,
解得.
故答案为:10.
12./
解:
=2(m2-9)
=2(m+3)(m-3).
故答案为:2(m+3)(m-3).
13.7
解:∵,
∴,
∴,
∴.
故答案为7.
14.7或-1
解:∵x2+2(m-3)x+16是关于x的完全平方式,
∴2(m-3)=±8,
解得:m=-1或7,
故答案为-1或7.
15.
解:由题得且,
解得:,
故答案为:.
16.14
解:∵垂直平分,
∴,
∴的周长=,
故答案为14.
17.九/9
解:,
∴这个多边形的边上是九.
故答案为:九.
18.
解:,
将代入得,原式.
19.,
解:
.
当时,原式.
20.x=-1.
解:方程两边同乘x-2,得2x=x-2+1
解这个方程,得x= -1
检验:x= -1时,x-2≠0
∴原方程的解是x= -1
21.(1)见解析(2)3
(1)证明: ∵等边△ABD和等边△ACE
∴AD=AB,AE=AC,∠DAB=∠EAC=60°
∴∠DAC=∠EAB
∴△DAC ≌△BAE
∴DC=BE
(2) 过点A作AH⊥BC于H
∵BD⊥BC
∴∠DBC=90°
∵等边△ABD
∴∠DBA=60° ,AB=BD=3
∴∠ABC=30°
∵AH⊥BC
∴AH= =
∴△ABC的面积=
22.(1)见解析
(2)见解析,
(3)5
(1)解:如图,即为所求;
(2)解:如图,点P即为所求.P坐标为,
故答案为.
(3)解:.
23.(1)见解析
(2)见解析
(1)证明:(1)∵DH垂直平分BC,且∠ABC=45°,
∴BD=DC,且∠BDC=90°,
∵∠A+∠ABF=90°,∠A+∠ACD=90°,
∴∠ABF=∠ACD,
在△BDF和△CDA中,
∴△BDF≌△CDA(ASA),
∴BF=AC.
(2)由(1)得BF=AC,
∵BE平分∠ABC,且BE⊥AC,
在△ABE和△CBE中,
∴△ABE≌△CBE(ASA),
∴.
∴BF=2CE.
24.(1)每件商品的进价为10元,每件商品的进价为5元
(2)种商品至少购进30件
(1)解:设每件商品的进价为元,则每件商品的进价为元,
根据题意,得,
解这个方程,得,
经检验,是原分式方程的解,且符合题意,
则,
答:每件商品的进价为10元,每件商品的进价为5元;
(2)解:设购进商品件,则购进商品件,
由题意,可得 ,
解得 ,
答:种商品至少购进30件.
25.(1)6
(2)或
(3)①证明见解析②的大小不变,总为,理由见解析
(1)解:,
,,
解得:,.
,,
的面积.
(2)当点C在上方时:
作为等腰直角三角形,过点作轴于F,轴于E,如图:
∴,
∵,
,,
,,
,
在和中,
,
,
,,
∵,
,即:,
解得:,
,,
;
当点C在下方时;
作为等腰直角三角形,过点作轴于F,轴于E,如图:
,,
,,
,
在和中,
,
,
,,
∵,
,
,即:,
解得:,
,
,
综上所述:点的坐标为:或.
(3)①延长,,它们相交于点,如图:
等腰直角中,,,且,
,
又,
,
在和中,
,
,
.
是的角平分线,
,
,
,
在和中,
,
,
即,
.
②的大小不变,总为,理由如下:
作,,垂足分别是,,如图:
,
由①可知:,,
在和中,
,
,
,
是的角平分线,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
