浙江省宁波市2024-2025学年上学期初二蛟川四校联考数学期末试卷(含答案)
文档属性
| 名称 | 浙江省宁波市2024-2025学年上学期初二蛟川四校联考数学期末试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 398.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 10:08:30 | ||
图片预览




文档简介
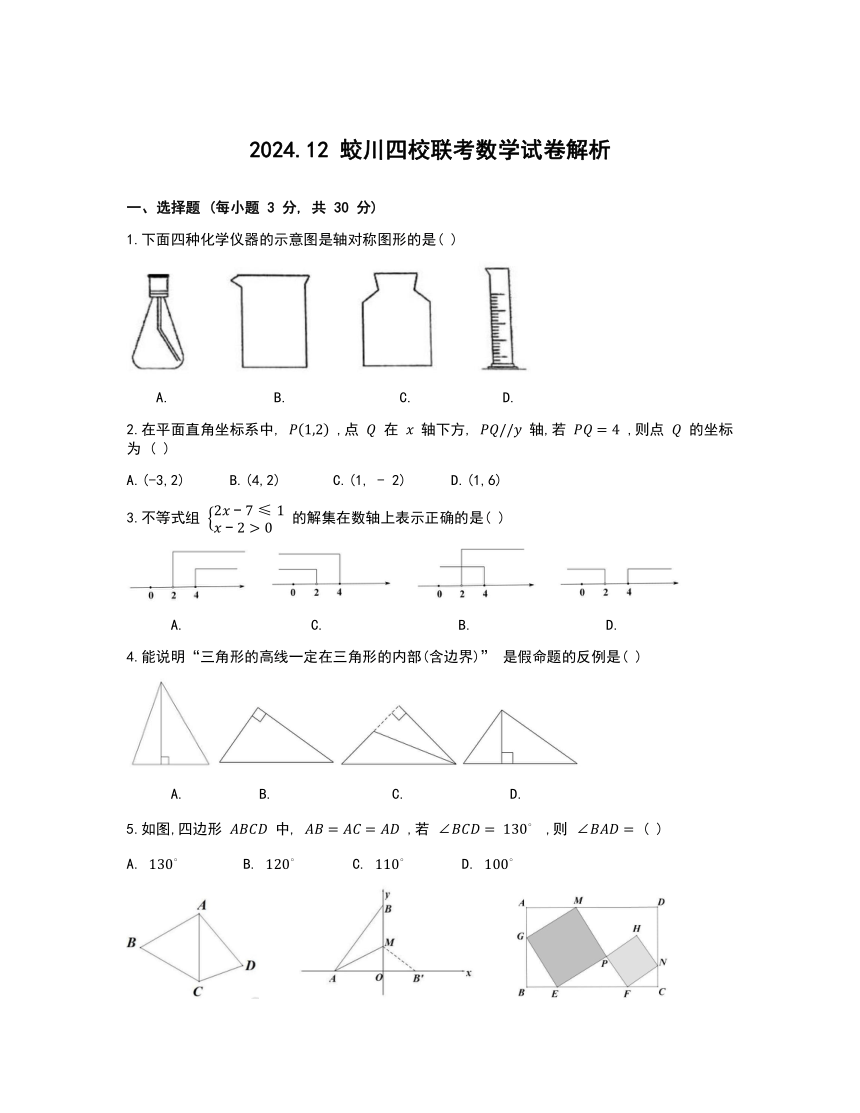
2024.12 蛟川四校联考数学试卷解析
一、选择题 (每小题 3 分, 共 30 分)
1.下面四种化学仪器的示意图是轴对称图形的是( )
B. C. D.
2.在平面直角坐标系中, ,点 在 轴下方, 轴,若 ,则点 的坐标为 ( )
A.(-3,2) B.(4,2) C.(1, - 2) D.(1,6)
3.不等式组 的解集在数轴上表示正确的是( )
C. B. D.
4.能说明“三角形的高线一定在三角形的内部(含边界)” 是假命题的反例是( )
B. C. D.
5.如图,四边形 中, ,若 ,则 ( )
A. B. C. D.
题5 题6 题8
6.如图,在平面直角坐标系中,点 的坐标是(-6,0), 点 的坐标是(0,8),点 是 上一点,将 沿 折叠,点 恰好落在轴上的点 处,则点 的坐标为 ( )
A.(3,0) B.(0,3) C.(4,0) D.(0,4)
7.将一箱苹果分给若干个学生,每个学生都分到苹果, 若每个学生分 4 个苹果, 则还剩 8 个苹果; 若每个学生分 5 个苹果, 则有一个学生所分苹果不足 2 个,若学生的人数为 ,则列式正确的是 ( )
A. B.
C. D.
8.如图,正方形 和正方形 的顶点 , 在长方形 的边上,已知 ,则 的面积为( )
A.16 B. 18 C.20 D. 24
9.关于 的一元一次不等式组 至少有 3 个整数解,则 的取值范围是( )
A. B. C. D.
10.如图,在 中, 为 上一点, 为 延长线上一点,连接 ,使得 . 若 ,且 ,则 的长为( )
A.6 B. C. D.
二、填空题 (每小题 4 分, 共 24 分)
11.用不等式表示“x 与 2 的差不足 10”:_____.
12.点 向左平移 7 个单位长度,再沿 轴对称后,得到点 的坐标,则点 的坐标为_____.
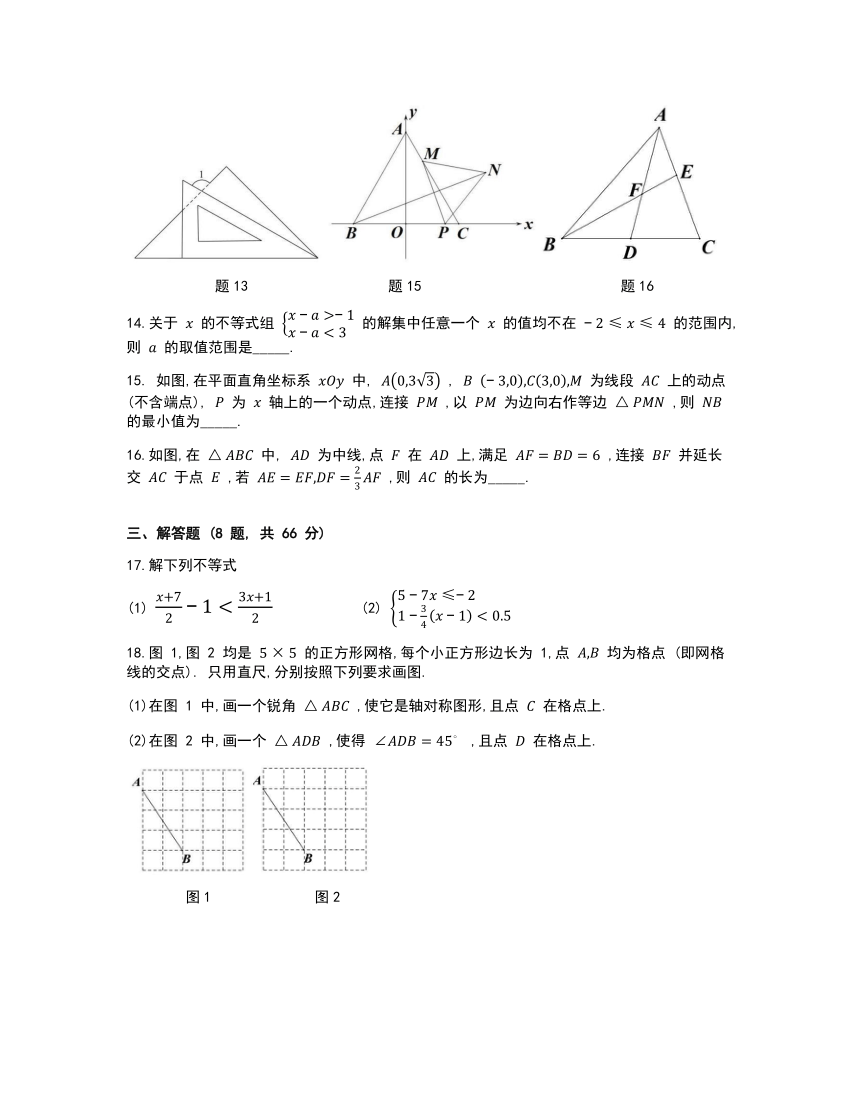
13.将一副三角尺按如图所示的方式叠放,则 的度数为_____.
题13 题15 题16
14.关于 的不等式组 的解集中任意一个 的值均不在 的范围内,则 的取值范围是_____.
15. 如图,在平面直角坐标系 中, , 为线段 上的动点 (不含端点), 为 轴上的一个动点,连接 ,以 为边向右作等边 ,则 的最小值为_____.
16.如图,在 中, 为中线,点 在 上,满足 ,连接 并延长交 于点 ,若 ,则 的长为_____.
三、解答题 (8 题, 共 66 分)
17.解下列不等式
(1) (2)
18.图 1,图 2 均是 的正方形网格,每个小正方形边长为 1,点 均为格点 (即网格线的交点). 只用直尺,分别按照下列要求画图.
(1)在图 1 中,画一个锐角 ,使它是轴对称图形,且点 在格点上.
(2)在图 2 中,画一个 ,使得 ,且点 在格点上.
图1 图2
19.已知: 如图,在 中, 于点 于点 ,交 于点 ,且 .
(1)求证: ;
(2)已知 ,求 的长.
20.已知方程组 的解满足 .
(1)求 的取值范围;
(2)当 为何整数时,不等式 的解集为 .
21.如图,在 中, ,点 在 上,
且 ,点 为 的中点, 是 上一点,满足 ,连接 并延长交 于点 ,若 ,求 的值.
22.根据以下素材,探索完成任务.
如何设计采购方案
素材 1 (个) 纪念品商店购进若干“忆江南”徽章和钥匙 销售阶段 徽 章 扣. 已知徽章的进价为 5 元/个, 吉祥物钥匙 扣的进价为 13 元/个, 如图表是近两周的销 售情况: 6 4 周 钥匙扣 (个) 2 6 销售收入一进货成本) 销售收 入(元) 120 220 (进价、售价均保持不变,利润
素材 2 该纪念品商店准备用不超过 532 元的金额再采购徽章和钥匙扣共 50 个.
问题解决
任务 1 请尝试求出“忆江南”徽章、钥匙扣的销售单价.
任务 2 该商店至少采购徽章多少个?
任务 3 请结合素材 2 中的消息, 帮助该纪念品商店设计采购方案, 使这 50 个纪念品 利润不低于 646 元, 请写出符合条件的采购方案.在这些采购方案中, 哪种方案 商店获利最高
23.在平面直角坐标系 中,对于点 , ,将 的值叫做点 与点 的“横纵距离”,记为 ,即 . 若点 在线段 上,将 的最大值与最小值之差称为线段 关于点 的“视差”,
记为 . 已知点 .
(1)点 与点 的“横纵距离” 的值为_____.
(2)已知点 在 轴上,线段 关于点 的“视差”为 2,则点 的坐标为_____;
(3)若点 与点 的“横纵距离”为 3.请在平面直角坐标系中画出所有符合题意的点 组成的图形,并计算得该图形的面积为_____.
24.如图一,在 中, 是 上一点,
点 在 上,且 ,点 是射线 上一动点.
(1)如图 1,若点 在 上,满足 ,求证: ;
(2)在(1)的条件下,若 ,求 的值;
(3)如图 2,若点 在 延长线上,满足 ,点 是 中点, , ,求 的面积.
试卷解析
一、选择题 (每小题 3 分, 共 30 分)
1. 选 C.
2. 选 C.
3. 选 B.
4. 选 C.
5. 选 D.
6. 选 B.
7.选 D.
8. 解析:
解: 过点 作 于点 ,
由一线三垂直模型易得 ,
同理 ,
设 ,
易得
①
,
②
联立①②得,解得
面积为 16,
选 .
9. 解析:
由不等式组 可得 ,
一元一次不等式组 至少有 3 个整数解.
所以 ,
选 B.
10. 解析:
如图,设 ,则 ,
.
在 Rt 中, .
过 作 垂直 于 ,设 ,则 ,
又 . 选 B.
二、填空题 (每小题 4 分, 共 24 分)
11.
12. (1,3)
13.
14. 或
15. 解析:
由主从动关系知 点轨迹为 所在直线,且 . 过 作 于 ,则 . .
16. 解析:
如图,倍长 到 ,使得 ,连接 . 则 ,所以 . 过 作 于 ,则 ,
在 Rt 中, ,
在 Rt 中, .
三、解答题 (8 题, 共 66 分)
17.(1) ; (2) .
18.
图1 图2
19. (1) ,
,
又 (AAS).
(2) .
20. (1) ;(2) .
21.
22.任务 1: “忆江南”徽章、钥匙扣的销售单价分别为 10 元和 30 元.
任务 2: 至少采购徽章 15 个.
任务 3: 采购徽章 15 个, 钥匙扣 35 个; 采购徽章 16 个, 钥匙扣 34 个; 采购徽章 17 个, 钥匙扣 33 个;
采购徽章 15 个, 钥匙扣 35 个的方案获利最高.
23.(1) .
(2)设 点坐标为(0, c)
①当 点在 点上方,由于 ,因此 ,
② 当 点在 点下方,由于 ,因此 ,所以点 的坐标为(0,3)或(0, - 2).
(3)
面积为 18 .
24. 解析:
(1) ,
,
又 .
(2)作过 点平行于 的平行线交 延长线于 ,如下图所示
,
,
设 ,则 ,
,即 ,解得: . 故 .
(3) 是 中点, 平分 ,
又 ,由勾股定理可得 ,
,可得 ,
又 ,
.
一、选择题 (每小题 3 分, 共 30 分)
1.下面四种化学仪器的示意图是轴对称图形的是( )
B. C. D.
2.在平面直角坐标系中, ,点 在 轴下方, 轴,若 ,则点 的坐标为 ( )
A.(-3,2) B.(4,2) C.(1, - 2) D.(1,6)
3.不等式组 的解集在数轴上表示正确的是( )
C. B. D.
4.能说明“三角形的高线一定在三角形的内部(含边界)” 是假命题的反例是( )
B. C. D.
5.如图,四边形 中, ,若 ,则 ( )
A. B. C. D.
题5 题6 题8
6.如图,在平面直角坐标系中,点 的坐标是(-6,0), 点 的坐标是(0,8),点 是 上一点,将 沿 折叠,点 恰好落在轴上的点 处,则点 的坐标为 ( )
A.(3,0) B.(0,3) C.(4,0) D.(0,4)
7.将一箱苹果分给若干个学生,每个学生都分到苹果, 若每个学生分 4 个苹果, 则还剩 8 个苹果; 若每个学生分 5 个苹果, 则有一个学生所分苹果不足 2 个,若学生的人数为 ,则列式正确的是 ( )
A. B.
C. D.
8.如图,正方形 和正方形 的顶点 , 在长方形 的边上,已知 ,则 的面积为( )
A.16 B. 18 C.20 D. 24
9.关于 的一元一次不等式组 至少有 3 个整数解,则 的取值范围是( )
A. B. C. D.
10.如图,在 中, 为 上一点, 为 延长线上一点,连接 ,使得 . 若 ,且 ,则 的长为( )
A.6 B. C. D.
二、填空题 (每小题 4 分, 共 24 分)
11.用不等式表示“x 与 2 的差不足 10”:_____.
12.点 向左平移 7 个单位长度,再沿 轴对称后,得到点 的坐标,则点 的坐标为_____.
13.将一副三角尺按如图所示的方式叠放,则 的度数为_____.
题13 题15 题16
14.关于 的不等式组 的解集中任意一个 的值均不在 的范围内,则 的取值范围是_____.
15. 如图,在平面直角坐标系 中, , 为线段 上的动点 (不含端点), 为 轴上的一个动点,连接 ,以 为边向右作等边 ,则 的最小值为_____.
16.如图,在 中, 为中线,点 在 上,满足 ,连接 并延长交 于点 ,若 ,则 的长为_____.
三、解答题 (8 题, 共 66 分)
17.解下列不等式
(1) (2)
18.图 1,图 2 均是 的正方形网格,每个小正方形边长为 1,点 均为格点 (即网格线的交点). 只用直尺,分别按照下列要求画图.
(1)在图 1 中,画一个锐角 ,使它是轴对称图形,且点 在格点上.
(2)在图 2 中,画一个 ,使得 ,且点 在格点上.
图1 图2
19.已知: 如图,在 中, 于点 于点 ,交 于点 ,且 .
(1)求证: ;
(2)已知 ,求 的长.
20.已知方程组 的解满足 .
(1)求 的取值范围;
(2)当 为何整数时,不等式 的解集为 .
21.如图,在 中, ,点 在 上,
且 ,点 为 的中点, 是 上一点,满足 ,连接 并延长交 于点 ,若 ,求 的值.
22.根据以下素材,探索完成任务.
如何设计采购方案
素材 1 (个) 纪念品商店购进若干“忆江南”徽章和钥匙 销售阶段 徽 章 扣. 已知徽章的进价为 5 元/个, 吉祥物钥匙 扣的进价为 13 元/个, 如图表是近两周的销 售情况: 6 4 周 钥匙扣 (个) 2 6 销售收入一进货成本) 销售收 入(元) 120 220 (进价、售价均保持不变,利润
素材 2 该纪念品商店准备用不超过 532 元的金额再采购徽章和钥匙扣共 50 个.
问题解决
任务 1 请尝试求出“忆江南”徽章、钥匙扣的销售单价.
任务 2 该商店至少采购徽章多少个?
任务 3 请结合素材 2 中的消息, 帮助该纪念品商店设计采购方案, 使这 50 个纪念品 利润不低于 646 元, 请写出符合条件的采购方案.在这些采购方案中, 哪种方案 商店获利最高
23.在平面直角坐标系 中,对于点 , ,将 的值叫做点 与点 的“横纵距离”,记为 ,即 . 若点 在线段 上,将 的最大值与最小值之差称为线段 关于点 的“视差”,
记为 . 已知点 .
(1)点 与点 的“横纵距离” 的值为_____.
(2)已知点 在 轴上,线段 关于点 的“视差”为 2,则点 的坐标为_____;
(3)若点 与点 的“横纵距离”为 3.请在平面直角坐标系中画出所有符合题意的点 组成的图形,并计算得该图形的面积为_____.
24.如图一,在 中, 是 上一点,
点 在 上,且 ,点 是射线 上一动点.
(1)如图 1,若点 在 上,满足 ,求证: ;
(2)在(1)的条件下,若 ,求 的值;
(3)如图 2,若点 在 延长线上,满足 ,点 是 中点, , ,求 的面积.
试卷解析
一、选择题 (每小题 3 分, 共 30 分)
1. 选 C.
2. 选 C.
3. 选 B.
4. 选 C.
5. 选 D.
6. 选 B.
7.选 D.
8. 解析:
解: 过点 作 于点 ,
由一线三垂直模型易得 ,
同理 ,
设 ,
易得
①
,
②
联立①②得,解得
面积为 16,
选 .
9. 解析:
由不等式组 可得 ,
一元一次不等式组 至少有 3 个整数解.
所以 ,
选 B.
10. 解析:
如图,设 ,则 ,
.
在 Rt 中, .
过 作 垂直 于 ,设 ,则 ,
又 . 选 B.
二、填空题 (每小题 4 分, 共 24 分)
11.
12. (1,3)
13.
14. 或
15. 解析:
由主从动关系知 点轨迹为 所在直线,且 . 过 作 于 ,则 . .
16. 解析:
如图,倍长 到 ,使得 ,连接 . 则 ,所以 . 过 作 于 ,则 ,
在 Rt 中, ,
在 Rt 中, .
三、解答题 (8 题, 共 66 分)
17.(1) ; (2) .
18.
图1 图2
19. (1) ,
,
又 (AAS).
(2) .
20. (1) ;(2) .
21.
22.任务 1: “忆江南”徽章、钥匙扣的销售单价分别为 10 元和 30 元.
任务 2: 至少采购徽章 15 个.
任务 3: 采购徽章 15 个, 钥匙扣 35 个; 采购徽章 16 个, 钥匙扣 34 个; 采购徽章 17 个, 钥匙扣 33 个;
采购徽章 15 个, 钥匙扣 35 个的方案获利最高.
23.(1) .
(2)设 点坐标为(0, c)
①当 点在 点上方,由于 ,因此 ,
② 当 点在 点下方,由于 ,因此 ,所以点 的坐标为(0,3)或(0, - 2).
(3)
面积为 18 .
24. 解析:
(1) ,
,
又 .
(2)作过 点平行于 的平行线交 延长线于 ,如下图所示
,
,
设 ,则 ,
,即 ,解得: . 故 .
(3) 是 中点, 平分 ,
又 ,由勾股定理可得 ,
,可得 ,
又 ,
.
同课章节目录
