高中物理 人教版(2019) 选择性必修 第一册 1.2动量定理 课件(共35张PPT)
文档属性
| 名称 | 高中物理 人教版(2019) 选择性必修 第一册 1.2动量定理 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 27.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-26 09:22:56 | ||
图片预览









文档简介
(共35张PPT)
1.2 动量定理
复习回顾:
1、什么是碰撞
2、如何猜想并探究碰撞中不变量?
3、碰撞中的不变量是什么?
4、什么是动量以及动量的特点?
5、如何求动量的变化?
6、动量和动能之间的数量关系?
问题一:鸡蛋在运输的时候为什么加上一层泡沫板?
问题二:船船和码头为什么常悬挂一些老旧轮胎?
其中有怎样的物理原理呢?你认为这样的相互作用过程中会涉及哪些量呢?
缓冲
问题三:头盔的内部为什么要放一层厚厚的海绵?
【探究1】在光滑水平面上的质量为m 的物体在水平恒力F 的作用下,经过时间t,速度由v 变为v′。试推导恒力F与物体动量变化量之间的关系。
【分析】如图所示,物体运动过程中:
由加速度的定义式:
由牛顿第二定律得:F = ma =
可得:Ft = mv′ - mv ,即:Ft = p′ - p
一、利用牛顿第二定律推导动量定理
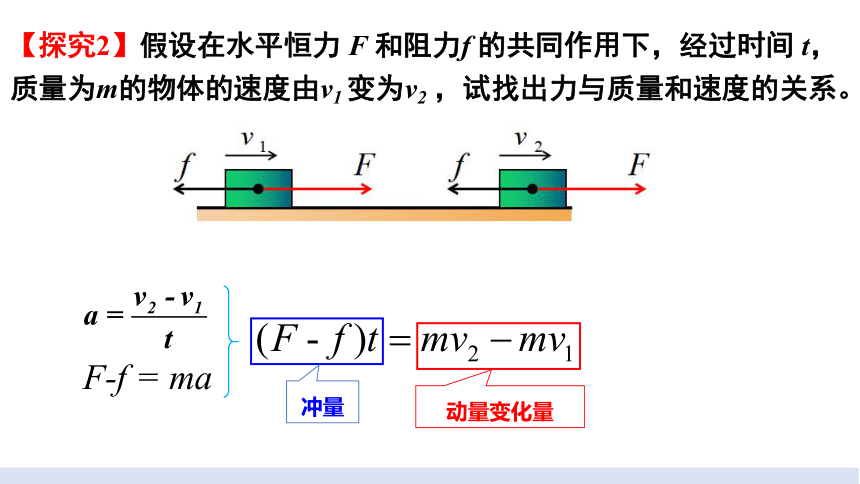
【探究2】假设在水平恒力 F 和阻力f 的共同作用下,经过时间 t,质量为m的物体的速度由v1 变为v2 ,试找出力与质量和速度的关系。
冲量
动量变化量
F-f = ma
以上推导表明动量的变化与力的时间积累效果有关。
看来Ft也是一个具有特殊意义的物理量,我们把Ft定义为冲量
1.定义:作用在物体上的力和作用时间的乘积,叫做该力对这个物体的冲量I。
3.单位:在国际单位制中,冲量的单位是牛·秒,符号是N·s
4.冲量是矢量:方向由力的方向决定,若为恒定方向的力,则冲量的方向跟这力的方向相同
5.冲量是过程量,反映了力对时间的积累效应。
想一想:之前学习过功W,它与冲量I有哪些异同?
2.公式: I=Ft (注:用该公式直接计算式要求F为恒力)
二、冲量
5.冲量与功的比较
冲量
功
区
别
公式
标、矢量
意义
正负
作用效果
单位
N·S
I=Ft
W=Flcos θ
矢量
标量
N·m(J)
力对时间的积累,对应一段时间
力对位移的积累,对应一段位移
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
改变物体的动量
改变物体的动能
①、作用力与反作用力:作用力的冲量与反作用力的冲量总是等值、反向并在同一条直线上,但是作用力的功与反作用力的功不一定相等。
②、内力:对物体系统内部,内力作用的冲量的矢量和等于零,但内力的功的代数和不一定为零。
例:人在船上行走——人对船的作用力与船对人的反作用力的冲量的矢量和等于零,但是人对船的作用力和船对人的反作用力都做正功,使人和船的动能都增加。
(1) 恒力的 冲量 公式法 利用定义式I=FΔt计算冲量,此方法仅适用于恒力的冲量的计算,无需考虑物体的运动状态
图像法 利用F-t图像中的“面积”来计算
三、冲量的求解方法
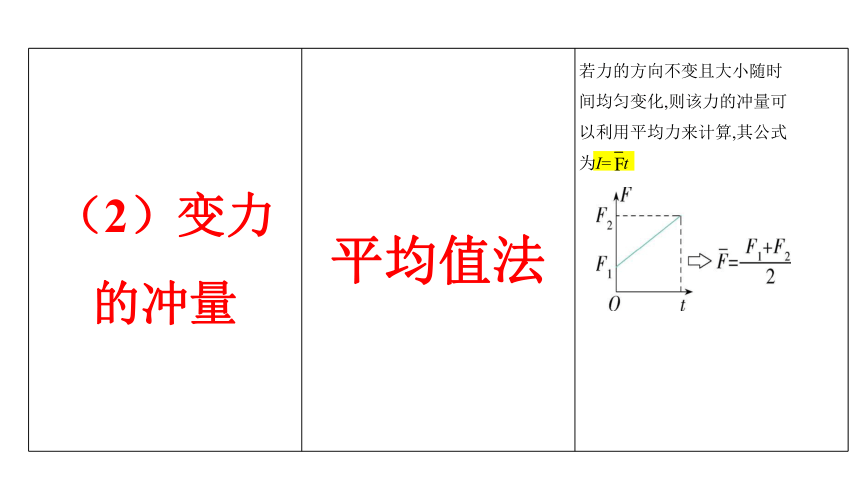
(2)变力的冲量 平均值法 若力的方向不变且大小随时
间均匀变化,则该力的冲量可
以利用平均力来计算,其公式
为I= t
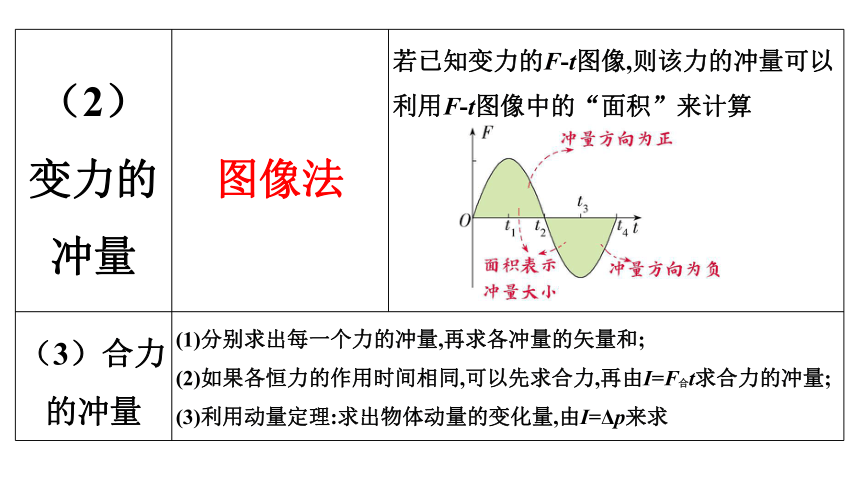
(2)变力的冲量 图像法 若已知变力的F-t图像,则该力的冲量可以利用F-t图像中的“面积”来计算
(3)合力的冲量 (1)分别求出每一个力的冲量,再求各冲量的矢量和; (2)如果各恒力的作用时间相同,可以先求合力,再由I=F合t求合力的冲量; (3)利用动量定理:求出物体动量的变化量,由I=Δp来求
例1、(多选)(2024·无锡高二检测)恒力F作用在质量为m的物体上,如图所示.由于地面对物体的摩擦力较大,物体没有被拉动,则经时间t,下列说法正确的是( )
A.拉力F对物体的冲量大小为零
B.拉力F对物体的冲量大小为Ft
C.拉力F对物体的冲量大小为Ftcosθ
D.合力对物体的冲量大小为零
BD
例2、(单选)如图所示,质量m=2kg的物体从倾角为θ=37o的固定斜面的顶端匀速滑下,下滑时间为t=1.5s,重力加速度g=10m/s2,下列说法中正确的是( )
A.支持力的冲量为零
B.摩擦力的冲量大小为 18N·s
C.重力的冲量大小为 18N·s
D.合力的冲量大小为30N·s
B
小结:1、F-t图线与时间轴之间所围的“面积”表示力F的冲量。
2、冲量是矢量,有方向,用正负表示方向。
例3、(多选)一质量为2kg的物块在合力F的作用下从静止开始沿直线运动,合力F随时间t变化的关系图像如图所示,则( )
A.0~2s时间内合力F对物块的冲量为3N·s
B.2~3s时间内合力F对物块的冲量为1N·s
C.0~3s时间内合力F对物块的冲量为2N·s
D.0~3s时间内合力F对物块的冲量为4N·s
AC
1.内容:物体所受合外力的冲量等于物体的动量变化,这就是动量定理。
2.表达式:
或
3.理解:
(1)表明合力的冲量是动量变化的原因;
(2)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同;
(3)动量的变化率:动量的变化跟发生这一变化所用的时间的比值。由动量定理,得 ,可见,动量的变化率等于物体所受的合力。当动量变化较快时,物体所受合力较大,反之较小;当动量均匀变化时,物体所受合力为恒力。
或
四、动量定理
例4、(单选)质量为m的篮球自由落下,以大小为v1的速度碰地,竖直向上弹回,碰撞时间极短,离地速度大小为v2.在碰撞过程中,地面对篮球的冲量的方向和大小为( )
A.向上,m(v1-v2) B.向上,m(v1+v2)
C.向下,m(v1-v2) D.向下,m(v1+v2)
【解析】选B.篮球与地面作用时受重力和地面的弹力,由于碰撞时间极短,重力的冲量可以忽略不计,选竖直向上为正方向,则IF=mv2-m(-v1)=m(v1+v2),冲量的方向与规定的正方向相同,竖直向上,故B正确,A、C、D错误.
B
动量定理解释生活现象
①△P一定,t短则F大,t长则F小;
由Ft=ΔP可知:
②t一定,F大则△P大,F小则△P小;
③F一定,t长则△P大,t短则△P小。
——缓冲装置
跳高比赛
跳远比赛
悬挂轮胎的游船准备靠岸
说一说:上述场景中的轮胎、垫子、沙坑的缓冲为什么可以保护好人和船不受到太大力的作用?请利用动量定理加以说明。
由Ft=Δp可知:
△p一定,t长则F小。
杂技表演时,常可看见有人用铁锤猛击放在“大力士”身上的大石块,石裂而人不伤,这是什么道理?
用铁锤猛击放在“大力上”身上的大石块,大石块受到很大的打击力而破裂,但是,根据动量定理得
对大石块来说,虽然受到的作用力F很大,但力作用时间极短,而大石块的质量又很大,因而引起的速度变化就很小,即大石块几乎没有向下运动,而且石块与人的身体接触面积又较大,据 ,所以人身体受的压强并不很大,故此人不会受伤(当然,这还和表演者技术本领有关).
例5、 (多选)利用动量定理对下列现象的解释,其中正确的是( )
A.击钉时,不用橡皮锤仅仅是因为橡皮锤太轻
B.用手接篮球时,手往往向后缩一下,是为了减小冲量
C.易碎品运输时,要用柔软材料包装,船舷常常悬挂旧轮胎,都是为了延长作用时间以减小作用力
D.在车内推车推不动,是因为车(包括人)所受合外力的冲量为零
CD
例6.将质量为m=1 kg的小球,从距水平地面高h=5 m处,以v0=10 m/s的水平速度抛出,不计空气阻力,g取10 m/s2。求:
(1)抛出后0.4 s内重力对小球的冲量;
(2)平抛运动过程中小球动量的增量Δp; (3)小球落地时的动量p'。
解析:(1)0.4 s内重力对小球的冲量I=mgt=1×10×0.4 N·s=4 N·s,方向竖直向下。
小球飞行过程中只受重力作用,所以合外力的冲量为
I'=mgt=1×10×1 N·s=10 N·s,方向竖直向下
由动量定理得Δp=I'=10 kg·m/s,方向竖直向下。
解析:(3)小球落地时竖直分速度为vy=gt=10 m/s。
方向与水平方向的夹角为45°。
小结:动量是矢量,既要给出其大小,也要说明其方向。
4.用动量定理解题的基本思路
特别说明 对过程较复杂的运动,可分段用动量定理,也可对整个过程用动量定理。
例7.(单选)物体A和B用轻绳相连,挂在轻弹簧下静止不动,如图(a)所示,A 的质量为m,B 的质量为M,当连接A、B的绳突然断开后,物体A上升经某一位置时的速度大小为v,这时物体B的下落速度大小为u,如图(b)所示,在这段时间里,弹簧的弹力对物体A的冲量为( )
A.Mv B.Mu
C.mv+Mu D. mv+mu
解析:对B由动量定理得:Mgt=Mu-0,设弹簧冲量为I,对A由动量定理得:I-mgt=mv-0,联立解得:I=mv+mu,ABC错误,D正确。
D
小结:①弹簧的弹力是变力,变力的冲量一般优先考虑用动量定理I=Δp求解。
②应用动量定理解题时,要注意正方向的选取。
③动量定理中的冲量是指物体所受合外力的冲量或物体所受外力的冲量的矢量和,故列方程前一定先对物体进行受力分析,正确认识物体的受力情况。
例8、 在水平力F=30 N的作用下,质量m=5 kg的物体由静止开始沿水平面运动.已知物体与水平面间的动摩擦因数μ=0.2,若F作用6 s后撤去,撤去F后物体还能向前运动多长时间才停止?(g取10 m/s2)
12 s
解析 解法一 用动量定理,分段求解.
选物体为研究对象,对于撤去F前物体做匀加速运动的过程,初态速度为零,末态速度为v.取水平力F的方向为正方向,根据动量定理有:(F-μmg)t1=mv-0,
对于撤去F后物体做匀减速运动的过程,初态速度为v,末态速度为零.根据动量定理有-μmgt2=0-mv.
解法二 用动量定理,研究全过程.
选物体为研究对象,研究整个运动过程,这个过程的始、末状态物体的速度都等于零.取水平力F的方向为正方向,根据动量定理得(F-μmg)t1+(-μmg)t2=0
五、动量定理在流体类问题中的应用
1.流体模型
对于流体的运动,可沿流速v的方向选取一段柱形流体,设在极短的时间Δt内通过某一面积为S的横截面的柱形流体的长度为Δl,如图所示。设流体的密度为ρ,则在Δt时间内流过该截面的流体的质量为Δm=ρSΔl=ρSvΔt,根据动量定理,可知流体微元所受的合外力的冲量等于该流体微元动量的变化量,即FΔt=ΔmΔv。
2.常见分两种情况:
(1)作用后流体微元静止,有Δv=-v,代入上式有F=-ρSv2;
(2)作用后流体微元以速率v反弹,有Δv=-2v,代入上式有
F=-2ρSv2。
2.微粒类问题
通常,电子流、光子流、离子流等被广义地视为“微粒”,其质量具有独立性,题目通常给出
单位体积内粒子数n。应用动量定理分析微粒类问题的步骤:
(1)建立“柱体”模型。沿微粒运动的方向选取微元,柱体的横截面积为S。
(2)选取微元研究。微元的长度为Δl=v0Δt,体积为ΔV=Sv0Δt,则微元内的粒子数N=nv0SΔt。
(3)先应用动量定理研究单个粒子,建立方程,再乘以N。
例9、(单选)在某些小区的自助洗车设备中,有一种是用高压水流冲洗汽车表面.今有一汽车高压水枪,设水枪喷水口横截面积为S,由枪口喷出的高压水流流速为v,假设水柱垂直喷射到汽车竖直的表面上,冲击汽车竖直表面后水的速度变为零,已知水的密度为ρ,则水柱对汽车竖直表面的平均冲击力为( )
A.ρSv 2 B.2ρSv 2 C.ρSv D.2ρSv
解析:以水柱运动方向为正方向
-Ft=0-mv
t 时间内喷水质量为m=ρSvt, 解得F=ρSv2
A
例10、假如有一宇宙飞船,它的正面面积为 S=1m ,以v=1×10 m/s的速度进入宇宙微粒尘区,尘区每1m 空间有一微粒,每一微粒平均质量m=1×10- g,若要使飞船速度保持不变,飞船的牵引力应增加多少 (设微粒与飞船相碰后附着到飞船上)
解:设飞船对微粒的作用力为F,牵引力应与微粒对飞船的作用力大小相等时间t内附着到飞船上的微粒数量n=S·vt,总质量为M=m·n
则由动量定理得: Ft=Mv,解得F=0.1N.
【方法与技巧】微粒类问题分析方法
通常,电子流、光子流、离子流等被广义地视为“微粒”,其质量具有独立性,题目通常给出单位体积内粒子数n。应用动量定理分析微粒类问题的步骤:
(1)建立“柱体”模型。沿微粒运动的方向选取微元,柱体的横截面积为S。
(2)选取微元研究。微元的长度为△l= v△t,体积为 △V=Svo△t,则微元内的粒子数 N=nvS△t。
(3)应用动量定理建立方程求解。
动量定理
基本
概念
动量
定理
动量:p=mv,状态量,矢量
适用恒力、
变力、直线
运动、曲线
运动等情况
冲量:I=Ft,过程量,矢量
内容:物体所受合力的冲量等于其动量的变化
表达式1:I合= Δ p
表达式2:F合t= mv′- mv
应用:解释现象、计算应用
【课堂小结】
1.2 动量定理
复习回顾:
1、什么是碰撞
2、如何猜想并探究碰撞中不变量?
3、碰撞中的不变量是什么?
4、什么是动量以及动量的特点?
5、如何求动量的变化?
6、动量和动能之间的数量关系?
问题一:鸡蛋在运输的时候为什么加上一层泡沫板?
问题二:船船和码头为什么常悬挂一些老旧轮胎?
其中有怎样的物理原理呢?你认为这样的相互作用过程中会涉及哪些量呢?
缓冲
问题三:头盔的内部为什么要放一层厚厚的海绵?
【探究1】在光滑水平面上的质量为m 的物体在水平恒力F 的作用下,经过时间t,速度由v 变为v′。试推导恒力F与物体动量变化量之间的关系。
【分析】如图所示,物体运动过程中:
由加速度的定义式:
由牛顿第二定律得:F = ma =
可得:Ft = mv′ - mv ,即:Ft = p′ - p
一、利用牛顿第二定律推导动量定理
【探究2】假设在水平恒力 F 和阻力f 的共同作用下,经过时间 t,质量为m的物体的速度由v1 变为v2 ,试找出力与质量和速度的关系。
冲量
动量变化量
F-f = ma
以上推导表明动量的变化与力的时间积累效果有关。
看来Ft也是一个具有特殊意义的物理量,我们把Ft定义为冲量
1.定义:作用在物体上的力和作用时间的乘积,叫做该力对这个物体的冲量I。
3.单位:在国际单位制中,冲量的单位是牛·秒,符号是N·s
4.冲量是矢量:方向由力的方向决定,若为恒定方向的力,则冲量的方向跟这力的方向相同
5.冲量是过程量,反映了力对时间的积累效应。
想一想:之前学习过功W,它与冲量I有哪些异同?
2.公式: I=Ft (注:用该公式直接计算式要求F为恒力)
二、冲量
5.冲量与功的比较
冲量
功
区
别
公式
标、矢量
意义
正负
作用效果
单位
N·S
I=Ft
W=Flcos θ
矢量
标量
N·m(J)
力对时间的积累,对应一段时间
力对位移的积累,对应一段位移
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
改变物体的动量
改变物体的动能
①、作用力与反作用力:作用力的冲量与反作用力的冲量总是等值、反向并在同一条直线上,但是作用力的功与反作用力的功不一定相等。
②、内力:对物体系统内部,内力作用的冲量的矢量和等于零,但内力的功的代数和不一定为零。
例:人在船上行走——人对船的作用力与船对人的反作用力的冲量的矢量和等于零,但是人对船的作用力和船对人的反作用力都做正功,使人和船的动能都增加。
(1) 恒力的 冲量 公式法 利用定义式I=FΔt计算冲量,此方法仅适用于恒力的冲量的计算,无需考虑物体的运动状态
图像法 利用F-t图像中的“面积”来计算
三、冲量的求解方法
(2)变力的冲量 平均值法 若力的方向不变且大小随时
间均匀变化,则该力的冲量可
以利用平均力来计算,其公式
为I= t
(2)变力的冲量 图像法 若已知变力的F-t图像,则该力的冲量可以利用F-t图像中的“面积”来计算
(3)合力的冲量 (1)分别求出每一个力的冲量,再求各冲量的矢量和; (2)如果各恒力的作用时间相同,可以先求合力,再由I=F合t求合力的冲量; (3)利用动量定理:求出物体动量的变化量,由I=Δp来求
例1、(多选)(2024·无锡高二检测)恒力F作用在质量为m的物体上,如图所示.由于地面对物体的摩擦力较大,物体没有被拉动,则经时间t,下列说法正确的是( )
A.拉力F对物体的冲量大小为零
B.拉力F对物体的冲量大小为Ft
C.拉力F对物体的冲量大小为Ftcosθ
D.合力对物体的冲量大小为零
BD
例2、(单选)如图所示,质量m=2kg的物体从倾角为θ=37o的固定斜面的顶端匀速滑下,下滑时间为t=1.5s,重力加速度g=10m/s2,下列说法中正确的是( )
A.支持力的冲量为零
B.摩擦力的冲量大小为 18N·s
C.重力的冲量大小为 18N·s
D.合力的冲量大小为30N·s
B
小结:1、F-t图线与时间轴之间所围的“面积”表示力F的冲量。
2、冲量是矢量,有方向,用正负表示方向。
例3、(多选)一质量为2kg的物块在合力F的作用下从静止开始沿直线运动,合力F随时间t变化的关系图像如图所示,则( )
A.0~2s时间内合力F对物块的冲量为3N·s
B.2~3s时间内合力F对物块的冲量为1N·s
C.0~3s时间内合力F对物块的冲量为2N·s
D.0~3s时间内合力F对物块的冲量为4N·s
AC
1.内容:物体所受合外力的冲量等于物体的动量变化,这就是动量定理。
2.表达式:
或
3.理解:
(1)表明合力的冲量是动量变化的原因;
(2)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同;
(3)动量的变化率:动量的变化跟发生这一变化所用的时间的比值。由动量定理,得 ,可见,动量的变化率等于物体所受的合力。当动量变化较快时,物体所受合力较大,反之较小;当动量均匀变化时,物体所受合力为恒力。
或
四、动量定理
例4、(单选)质量为m的篮球自由落下,以大小为v1的速度碰地,竖直向上弹回,碰撞时间极短,离地速度大小为v2.在碰撞过程中,地面对篮球的冲量的方向和大小为( )
A.向上,m(v1-v2) B.向上,m(v1+v2)
C.向下,m(v1-v2) D.向下,m(v1+v2)
【解析】选B.篮球与地面作用时受重力和地面的弹力,由于碰撞时间极短,重力的冲量可以忽略不计,选竖直向上为正方向,则IF=mv2-m(-v1)=m(v1+v2),冲量的方向与规定的正方向相同,竖直向上,故B正确,A、C、D错误.
B
动量定理解释生活现象
①△P一定,t短则F大,t长则F小;
由Ft=ΔP可知:
②t一定,F大则△P大,F小则△P小;
③F一定,t长则△P大,t短则△P小。
——缓冲装置
跳高比赛
跳远比赛
悬挂轮胎的游船准备靠岸
说一说:上述场景中的轮胎、垫子、沙坑的缓冲为什么可以保护好人和船不受到太大力的作用?请利用动量定理加以说明。
由Ft=Δp可知:
△p一定,t长则F小。
杂技表演时,常可看见有人用铁锤猛击放在“大力士”身上的大石块,石裂而人不伤,这是什么道理?
用铁锤猛击放在“大力上”身上的大石块,大石块受到很大的打击力而破裂,但是,根据动量定理得
对大石块来说,虽然受到的作用力F很大,但力作用时间极短,而大石块的质量又很大,因而引起的速度变化就很小,即大石块几乎没有向下运动,而且石块与人的身体接触面积又较大,据 ,所以人身体受的压强并不很大,故此人不会受伤(当然,这还和表演者技术本领有关).
例5、 (多选)利用动量定理对下列现象的解释,其中正确的是( )
A.击钉时,不用橡皮锤仅仅是因为橡皮锤太轻
B.用手接篮球时,手往往向后缩一下,是为了减小冲量
C.易碎品运输时,要用柔软材料包装,船舷常常悬挂旧轮胎,都是为了延长作用时间以减小作用力
D.在车内推车推不动,是因为车(包括人)所受合外力的冲量为零
CD
例6.将质量为m=1 kg的小球,从距水平地面高h=5 m处,以v0=10 m/s的水平速度抛出,不计空气阻力,g取10 m/s2。求:
(1)抛出后0.4 s内重力对小球的冲量;
(2)平抛运动过程中小球动量的增量Δp; (3)小球落地时的动量p'。
解析:(1)0.4 s内重力对小球的冲量I=mgt=1×10×0.4 N·s=4 N·s,方向竖直向下。
小球飞行过程中只受重力作用,所以合外力的冲量为
I'=mgt=1×10×1 N·s=10 N·s,方向竖直向下
由动量定理得Δp=I'=10 kg·m/s,方向竖直向下。
解析:(3)小球落地时竖直分速度为vy=gt=10 m/s。
方向与水平方向的夹角为45°。
小结:动量是矢量,既要给出其大小,也要说明其方向。
4.用动量定理解题的基本思路
特别说明 对过程较复杂的运动,可分段用动量定理,也可对整个过程用动量定理。
例7.(单选)物体A和B用轻绳相连,挂在轻弹簧下静止不动,如图(a)所示,A 的质量为m,B 的质量为M,当连接A、B的绳突然断开后,物体A上升经某一位置时的速度大小为v,这时物体B的下落速度大小为u,如图(b)所示,在这段时间里,弹簧的弹力对物体A的冲量为( )
A.Mv B.Mu
C.mv+Mu D. mv+mu
解析:对B由动量定理得:Mgt=Mu-0,设弹簧冲量为I,对A由动量定理得:I-mgt=mv-0,联立解得:I=mv+mu,ABC错误,D正确。
D
小结:①弹簧的弹力是变力,变力的冲量一般优先考虑用动量定理I=Δp求解。
②应用动量定理解题时,要注意正方向的选取。
③动量定理中的冲量是指物体所受合外力的冲量或物体所受外力的冲量的矢量和,故列方程前一定先对物体进行受力分析,正确认识物体的受力情况。
例8、 在水平力F=30 N的作用下,质量m=5 kg的物体由静止开始沿水平面运动.已知物体与水平面间的动摩擦因数μ=0.2,若F作用6 s后撤去,撤去F后物体还能向前运动多长时间才停止?(g取10 m/s2)
12 s
解析 解法一 用动量定理,分段求解.
选物体为研究对象,对于撤去F前物体做匀加速运动的过程,初态速度为零,末态速度为v.取水平力F的方向为正方向,根据动量定理有:(F-μmg)t1=mv-0,
对于撤去F后物体做匀减速运动的过程,初态速度为v,末态速度为零.根据动量定理有-μmgt2=0-mv.
解法二 用动量定理,研究全过程.
选物体为研究对象,研究整个运动过程,这个过程的始、末状态物体的速度都等于零.取水平力F的方向为正方向,根据动量定理得(F-μmg)t1+(-μmg)t2=0
五、动量定理在流体类问题中的应用
1.流体模型
对于流体的运动,可沿流速v的方向选取一段柱形流体,设在极短的时间Δt内通过某一面积为S的横截面的柱形流体的长度为Δl,如图所示。设流体的密度为ρ,则在Δt时间内流过该截面的流体的质量为Δm=ρSΔl=ρSvΔt,根据动量定理,可知流体微元所受的合外力的冲量等于该流体微元动量的变化量,即FΔt=ΔmΔv。
2.常见分两种情况:
(1)作用后流体微元静止,有Δv=-v,代入上式有F=-ρSv2;
(2)作用后流体微元以速率v反弹,有Δv=-2v,代入上式有
F=-2ρSv2。
2.微粒类问题
通常,电子流、光子流、离子流等被广义地视为“微粒”,其质量具有独立性,题目通常给出
单位体积内粒子数n。应用动量定理分析微粒类问题的步骤:
(1)建立“柱体”模型。沿微粒运动的方向选取微元,柱体的横截面积为S。
(2)选取微元研究。微元的长度为Δl=v0Δt,体积为ΔV=Sv0Δt,则微元内的粒子数N=nv0SΔt。
(3)先应用动量定理研究单个粒子,建立方程,再乘以N。
例9、(单选)在某些小区的自助洗车设备中,有一种是用高压水流冲洗汽车表面.今有一汽车高压水枪,设水枪喷水口横截面积为S,由枪口喷出的高压水流流速为v,假设水柱垂直喷射到汽车竖直的表面上,冲击汽车竖直表面后水的速度变为零,已知水的密度为ρ,则水柱对汽车竖直表面的平均冲击力为( )
A.ρSv 2 B.2ρSv 2 C.ρSv D.2ρSv
解析:以水柱运动方向为正方向
-Ft=0-mv
t 时间内喷水质量为m=ρSvt, 解得F=ρSv2
A
例10、假如有一宇宙飞船,它的正面面积为 S=1m ,以v=1×10 m/s的速度进入宇宙微粒尘区,尘区每1m 空间有一微粒,每一微粒平均质量m=1×10- g,若要使飞船速度保持不变,飞船的牵引力应增加多少 (设微粒与飞船相碰后附着到飞船上)
解:设飞船对微粒的作用力为F,牵引力应与微粒对飞船的作用力大小相等时间t内附着到飞船上的微粒数量n=S·vt,总质量为M=m·n
则由动量定理得: Ft=Mv,解得F=0.1N.
【方法与技巧】微粒类问题分析方法
通常,电子流、光子流、离子流等被广义地视为“微粒”,其质量具有独立性,题目通常给出单位体积内粒子数n。应用动量定理分析微粒类问题的步骤:
(1)建立“柱体”模型。沿微粒运动的方向选取微元,柱体的横截面积为S。
(2)选取微元研究。微元的长度为△l= v△t,体积为 △V=Svo△t,则微元内的粒子数 N=nvS△t。
(3)应用动量定理建立方程求解。
动量定理
基本
概念
动量
定理
动量:p=mv,状态量,矢量
适用恒力、
变力、直线
运动、曲线
运动等情况
冲量:I=Ft,过程量,矢量
内容:物体所受合力的冲量等于其动量的变化
表达式1:I合= Δ p
表达式2:F合t= mv′- mv
应用:解释现象、计算应用
【课堂小结】
