第31讲 平移 对称 旋转课件2025年中考数学人教版一轮复习(共26张PPT)
文档属性
| 名称 | 第31讲 平移 对称 旋转课件2025年中考数学人教版一轮复习(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第八章 图形与变换
第31讲 平移 对称 旋转
1. 通过具体实例了解轴对称和中心对称以及轴对称图形和中心对称图形
的概念,探索它们的基本性质.
2. 能画出简单平面图形(点、线段、直线、三角形等)关于给定对称轴的
对称图形.
3. 通过具体实例认识平移、认识平面图形关于旋转中心的旋转,探索它
的基本性质.
4. 在平面直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标
的多边形的对称图形的顶点坐标,并知道对应顶点之间的关系.
5. 在平面直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方
向平移后图形的顶点坐标,并知道对应顶点坐标之间的关系.
6. 在平面直角坐标系中,探索并了解将一个多边形依次沿两个坐标轴方
向平移后所得到的图形与原来的图形具有平移关系,体会图形顶点坐标
的变化.
1. 图形的轴对称
定
义 如果把一个图形沿着某一条直线折叠,与另一个图形重合,那么就
说这两个图形关于这条直线(成轴)对称
性
质 ①轴对称的两个图形是全等图形;②对称轴是对应点所连线段的垂
直平分线
1. (2024·青海中考)如图,一次函数y=2x-3的图象与x轴相交于点A,
则点A关于y轴的对称点的坐标是( A )
A. (- ,0) B. (,0)
C. (0,3) D. (0,-3)
A
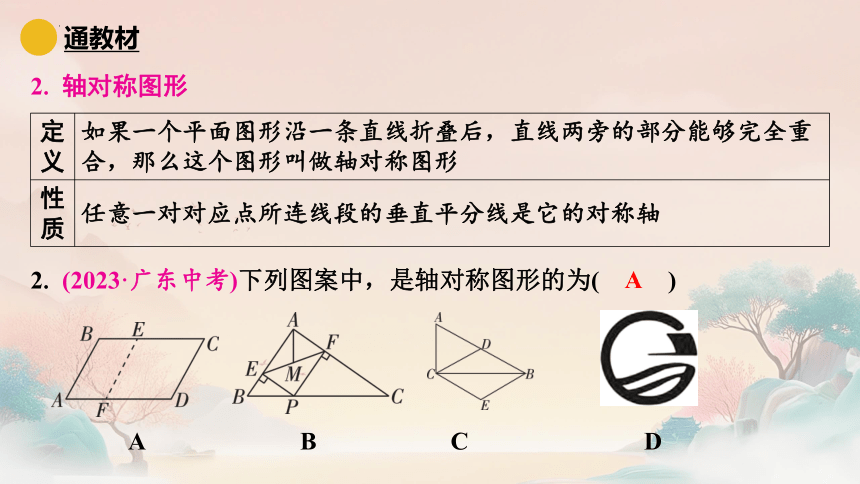
2. 轴对称图形
定
义 如果一个平面图形沿一条直线折叠后,直线两旁的部分能够完全重
合,那么这个图形叫做轴对称图形
性
质 任意一对对应点所连线段的垂直平分线是它的对称轴
2. (2023·广东中考)下列图案中,是轴对称图形的为( A )
A B C D
A
3. 中心对称(特殊的旋转)
定
义 把一个图形绕着某一点旋转,如果它能够和另一个图形重合,那么
我们称这两个图形关于这个点对称或成中心对称
性
质 ①中心对称的两个图形,对应点所连线段都经过对称中心,且被对
称中心平分;②成中心对称的两个图形是全等图形
3. (2023·广州名校三模)如图,将△ABC绕点C(0,-1)旋转180°得到
△A'B'C. 设点A'的坐标为(a,b),则点A的坐标为( D )
A. (-a,-b) B. (-a,-b-1)
C. (-a,-b+1) D. (-a,-b-2)
D
4. 中心对称图形
定
义 在平面内,把一个图形绕某个点旋转,如果旋转后的图形和原图形
重合,那么这个图形叫做中心对称图形
性
质 在中心对称图形中,对应点所连线段经过对称中心,且被对称中心
平分
4. (2024·无锡中考)下列图形是中心对称图形的是( C )
A. 等边三角形 B. 直角三角形
C. 平行四边形 D. 正五边形
C
5. 图形的平移
定
义 把一个图形沿某个方向移动一定的距离,这个图形的运动称为平移
要
素 ①平移方向;②平移距离
性
质 ①平移前后图形全等;②对应点所连的线段平行或在一条直线上且
相等
5. 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.F是AB的
中点,连接CF,把线段CF沿射线BC方向平移到DE,点D在AC上,
则线段CF在平移过程中扫过区域形成的四边形CFDE的面积是( C )
A. 6 B. 18 C. 12 D. 16
C
6. 图形的旋转
定义 在平面内,把一个图形绕一个定点,沿某个方向旋转一个角度,这个图形的运动称为旋转
要素 ①旋转中心;②旋转方向;③旋转角
性质 ①旋转前后图形全等;
②对应点到旋转中心的距离相等;
③任意一对对应点与旋转中心连线所成的角都等于旋转角
6. (2024·无锡中考)如图,在△ABC中,∠B=80°,∠C=65°,将
△ABC绕点A逆时针旋转得到△AB'C'.当AB'落在AC上时,∠BAC'的度
数为( B )
A. 65° B. 70° C. 80° D. 85°
B
【核心考点1】平移的性质
1. (2024·黄埔期末)如图,将Rt△ABC沿着点B到点C的方向平移到
△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分的面积为
( C )
A. 42 B. 96
C
C. 48 D. 84
【变式1】(2023·深圳中考)如图,在平行四边形ABCD中,AB=4,BC
=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形
ECDF为菱形时,则a的值为( B )
A. 1 B. 2 C. 3 D. 4
B
【核心考点2】轴对称与中心对称图形
2. (2024·潍坊中考)下列著名曲线中,既是轴对称图形也是中心对称图形
的是( C )
A B C D
【变式2】下列图形中,既是轴对称图形又是中心对称图形的是( B )
A B C D
C
B
【核心考点3】旋转的性质
3. (2024·广元中考)如图,将△ABC绕点A顺时针旋转90°得到△ADE,
点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上.
若CD=3,BC=1,则AD的长为( A )
A. B. C. 2 D. 2
第3题图
A
【变式3】(2023·张家界中考)如图,AO为∠BAC的平分线,且∠BAC=
50°,将四边形ABOC绕点A逆时针方向旋转后,得到四边形AB'O'C',
且∠OAC'=100°,则四边形ABOC旋转的角度是 .
变式3图
75°
【核心考点4】几何变换作图
4. (2023·黑龙江中考节选)如图,在平面直角坐标系中,已知△ABC的三
个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将△ABC向上平移4个单位长度,再向右平移1个单位长度,得到
△A1B1C1,请画出△A1B1C1;
解:(1)如图1所示,△A1B1C1即为所求.
解:(1)如图1所示,△A1B1C1即为所求.
(2)请画出△ABC关于y轴对称的△A2B2C2.
4. (2023·黑龙江中考节选)如图,在平面直角坐标系中,已知△ABC的三
个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
解:(2)如图2所示,△A2B2C2即为所求.
【变式4】(2023·达州中考)如图,网格中每个小正方形的边长均为1,
△ABC的顶点均在小正方形的顶点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
解:(1)如图1,△A1B1C1即为所求.
图1 图2
解:(1)如图1,△A1B1C1即为所求.
图1 图2
(2)将△ABC绕点C顺时针旋转90°得到△A2B2C2,画出△A2B2C2.
解:(2)如图2,
△A2B2C2即为
所求.
5. 如图,将△ABC向右平移a cm(a>0)得到△DEF,连接AD. 若△ABC
的周长是36 cm,则四边形ABFD的周长是( C )
A. (36+a)cm B. (72+a)cm
C. (36+2a)cm D. (72+2a)cm
第5题图
C
6. (2023·荆州中考)如图,直线y=- x+3分别与x轴、y轴交于点A,
B,将△OAB绕着点A顺时针旋转90°得到△CAD,则点B的对应点D
的坐标是( C )
A. (2,5) B. (3,5)
C. (5,2) D. (,2)
第6题图
C
7. (2023·黑龙江中考)如图,在平面直角坐标系中,矩形ABCD的边AD
=5,OA∶OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位
置,线段OD1恰好经过点B,点C落在y轴上的点C1位置,点E的坐标是
( D )
D
第7题图
A. (1,2) B. (-1,2)
C. (-1,2) D. (1- ,2)
8. 如图,在Rt△ACB中,∠BAC=30°,CB=4,E是斜边AB的中
点,将Rt△ACB绕点A顺时针旋转得Rt△ADF,点C,B旋转后的对应
点分别是点D,F,连接CF,EF,CE,求旋转的过程中△CEF的面
积的最大值.
解:如图,过点A作AG⊥CE交CE的延长线于点G.
在Rt△ACB中,∠BAC=30°,CB=4,E是斜边AB的中点,
∴AB=2CB=8,
∴CE= AB=4=AE,AC= =4 ,
∴∠ECA=∠BAC=30°,
∴AG= AC=2 ,
由旋转的性质可得AF=AB=8,
当EF⊥CE时,△CEF的面积最大,
∴点F到直线CE的距离的最大值为FG=AF+AG=8+
2 ,(如图,G,A,F三点共线时)
∴△CEF的面积的最大值= CE×(8+2 )
= ×4×(8+2 )=16+4 .
∴点F到直线CE的距离的最大值为FG=AF+AG
=8+2 ,(如图,G,A,F三点共线时)
∴△CEF的面积的最大值= CE×(8+2 )
= ×4×(8+2 )=16+4 .
第八章 图形与变换
第31讲 平移 对称 旋转
1. 通过具体实例了解轴对称和中心对称以及轴对称图形和中心对称图形
的概念,探索它们的基本性质.
2. 能画出简单平面图形(点、线段、直线、三角形等)关于给定对称轴的
对称图形.
3. 通过具体实例认识平移、认识平面图形关于旋转中心的旋转,探索它
的基本性质.
4. 在平面直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标
的多边形的对称图形的顶点坐标,并知道对应顶点之间的关系.
5. 在平面直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方
向平移后图形的顶点坐标,并知道对应顶点坐标之间的关系.
6. 在平面直角坐标系中,探索并了解将一个多边形依次沿两个坐标轴方
向平移后所得到的图形与原来的图形具有平移关系,体会图形顶点坐标
的变化.
1. 图形的轴对称
定
义 如果把一个图形沿着某一条直线折叠,与另一个图形重合,那么就
说这两个图形关于这条直线(成轴)对称
性
质 ①轴对称的两个图形是全等图形;②对称轴是对应点所连线段的垂
直平分线
1. (2024·青海中考)如图,一次函数y=2x-3的图象与x轴相交于点A,
则点A关于y轴的对称点的坐标是( A )
A. (- ,0) B. (,0)
C. (0,3) D. (0,-3)
A
2. 轴对称图形
定
义 如果一个平面图形沿一条直线折叠后,直线两旁的部分能够完全重
合,那么这个图形叫做轴对称图形
性
质 任意一对对应点所连线段的垂直平分线是它的对称轴
2. (2023·广东中考)下列图案中,是轴对称图形的为( A )
A B C D
A
3. 中心对称(特殊的旋转)
定
义 把一个图形绕着某一点旋转,如果它能够和另一个图形重合,那么
我们称这两个图形关于这个点对称或成中心对称
性
质 ①中心对称的两个图形,对应点所连线段都经过对称中心,且被对
称中心平分;②成中心对称的两个图形是全等图形
3. (2023·广州名校三模)如图,将△ABC绕点C(0,-1)旋转180°得到
△A'B'C. 设点A'的坐标为(a,b),则点A的坐标为( D )
A. (-a,-b) B. (-a,-b-1)
C. (-a,-b+1) D. (-a,-b-2)
D
4. 中心对称图形
定
义 在平面内,把一个图形绕某个点旋转,如果旋转后的图形和原图形
重合,那么这个图形叫做中心对称图形
性
质 在中心对称图形中,对应点所连线段经过对称中心,且被对称中心
平分
4. (2024·无锡中考)下列图形是中心对称图形的是( C )
A. 等边三角形 B. 直角三角形
C. 平行四边形 D. 正五边形
C
5. 图形的平移
定
义 把一个图形沿某个方向移动一定的距离,这个图形的运动称为平移
要
素 ①平移方向;②平移距离
性
质 ①平移前后图形全等;②对应点所连的线段平行或在一条直线上且
相等
5. 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.F是AB的
中点,连接CF,把线段CF沿射线BC方向平移到DE,点D在AC上,
则线段CF在平移过程中扫过区域形成的四边形CFDE的面积是( C )
A. 6 B. 18 C. 12 D. 16
C
6. 图形的旋转
定义 在平面内,把一个图形绕一个定点,沿某个方向旋转一个角度,这个图形的运动称为旋转
要素 ①旋转中心;②旋转方向;③旋转角
性质 ①旋转前后图形全等;
②对应点到旋转中心的距离相等;
③任意一对对应点与旋转中心连线所成的角都等于旋转角
6. (2024·无锡中考)如图,在△ABC中,∠B=80°,∠C=65°,将
△ABC绕点A逆时针旋转得到△AB'C'.当AB'落在AC上时,∠BAC'的度
数为( B )
A. 65° B. 70° C. 80° D. 85°
B
【核心考点1】平移的性质
1. (2024·黄埔期末)如图,将Rt△ABC沿着点B到点C的方向平移到
△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分的面积为
( C )
A. 42 B. 96
C
C. 48 D. 84
【变式1】(2023·深圳中考)如图,在平行四边形ABCD中,AB=4,BC
=6,将线段AB水平向右平移a个单位长度得到线段EF,若四边形
ECDF为菱形时,则a的值为( B )
A. 1 B. 2 C. 3 D. 4
B
【核心考点2】轴对称与中心对称图形
2. (2024·潍坊中考)下列著名曲线中,既是轴对称图形也是中心对称图形
的是( C )
A B C D
【变式2】下列图形中,既是轴对称图形又是中心对称图形的是( B )
A B C D
C
B
【核心考点3】旋转的性质
3. (2024·广元中考)如图,将△ABC绕点A顺时针旋转90°得到△ADE,
点B,C的对应点分别为点D,E,连接CE,点D恰好落在线段CE上.
若CD=3,BC=1,则AD的长为( A )
A. B. C. 2 D. 2
第3题图
A
【变式3】(2023·张家界中考)如图,AO为∠BAC的平分线,且∠BAC=
50°,将四边形ABOC绕点A逆时针方向旋转后,得到四边形AB'O'C',
且∠OAC'=100°,则四边形ABOC旋转的角度是 .
变式3图
75°
【核心考点4】几何变换作图
4. (2023·黑龙江中考节选)如图,在平面直角坐标系中,已知△ABC的三
个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将△ABC向上平移4个单位长度,再向右平移1个单位长度,得到
△A1B1C1,请画出△A1B1C1;
解:(1)如图1所示,△A1B1C1即为所求.
解:(1)如图1所示,△A1B1C1即为所求.
(2)请画出△ABC关于y轴对称的△A2B2C2.
4. (2023·黑龙江中考节选)如图,在平面直角坐标系中,已知△ABC的三
个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
解:(2)如图2所示,△A2B2C2即为所求.
【变式4】(2023·达州中考)如图,网格中每个小正方形的边长均为1,
△ABC的顶点均在小正方形的顶点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
解:(1)如图1,△A1B1C1即为所求.
图1 图2
解:(1)如图1,△A1B1C1即为所求.
图1 图2
(2)将△ABC绕点C顺时针旋转90°得到△A2B2C2,画出△A2B2C2.
解:(2)如图2,
△A2B2C2即为
所求.
5. 如图,将△ABC向右平移a cm(a>0)得到△DEF,连接AD. 若△ABC
的周长是36 cm,则四边形ABFD的周长是( C )
A. (36+a)cm B. (72+a)cm
C. (36+2a)cm D. (72+2a)cm
第5题图
C
6. (2023·荆州中考)如图,直线y=- x+3分别与x轴、y轴交于点A,
B,将△OAB绕着点A顺时针旋转90°得到△CAD,则点B的对应点D
的坐标是( C )
A. (2,5) B. (3,5)
C. (5,2) D. (,2)
第6题图
C
7. (2023·黑龙江中考)如图,在平面直角坐标系中,矩形ABCD的边AD
=5,OA∶OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位
置,线段OD1恰好经过点B,点C落在y轴上的点C1位置,点E的坐标是
( D )
D
第7题图
A. (1,2) B. (-1,2)
C. (-1,2) D. (1- ,2)
8. 如图,在Rt△ACB中,∠BAC=30°,CB=4,E是斜边AB的中
点,将Rt△ACB绕点A顺时针旋转得Rt△ADF,点C,B旋转后的对应
点分别是点D,F,连接CF,EF,CE,求旋转的过程中△CEF的面
积的最大值.
解:如图,过点A作AG⊥CE交CE的延长线于点G.
在Rt△ACB中,∠BAC=30°,CB=4,E是斜边AB的中点,
∴AB=2CB=8,
∴CE= AB=4=AE,AC= =4 ,
∴∠ECA=∠BAC=30°,
∴AG= AC=2 ,
由旋转的性质可得AF=AB=8,
当EF⊥CE时,△CEF的面积最大,
∴点F到直线CE的距离的最大值为FG=AF+AG=8+
2 ,(如图,G,A,F三点共线时)
∴△CEF的面积的最大值= CE×(8+2 )
= ×4×(8+2 )=16+4 .
∴点F到直线CE的距离的最大值为FG=AF+AG
=8+2 ,(如图,G,A,F三点共线时)
∴△CEF的面积的最大值= CE×(8+2 )
= ×4×(8+2 )=16+4 .
同课章节目录
