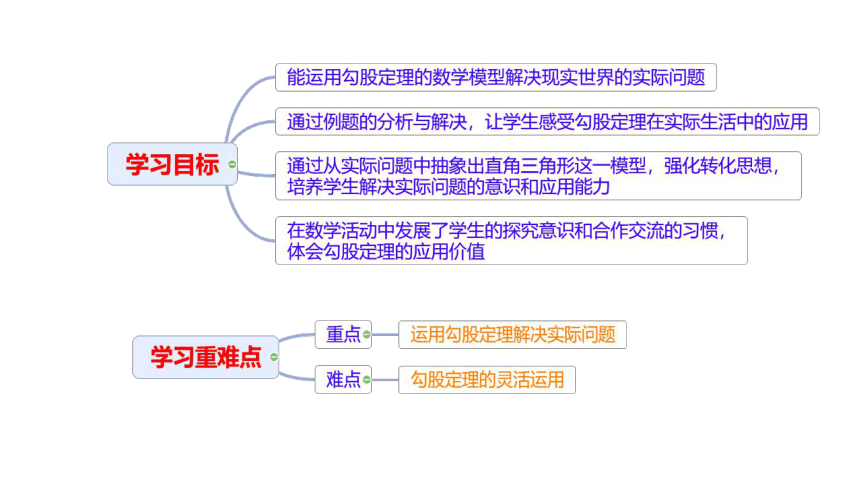
北师大版数学八年级上册1.3 勾股定理的应用课件(共24张PPT)
文档属性
| 名称 | 北师大版数学八年级上册1.3 勾股定理的应用课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
勾股定理的应用
湖中红莲露一尺,忽被强风吹一边,
花离原位三尺远,湖水如何知深浅?
A
D
C
B
1
勾股应用之旅
初出茅庐站
1
初出茅庐站
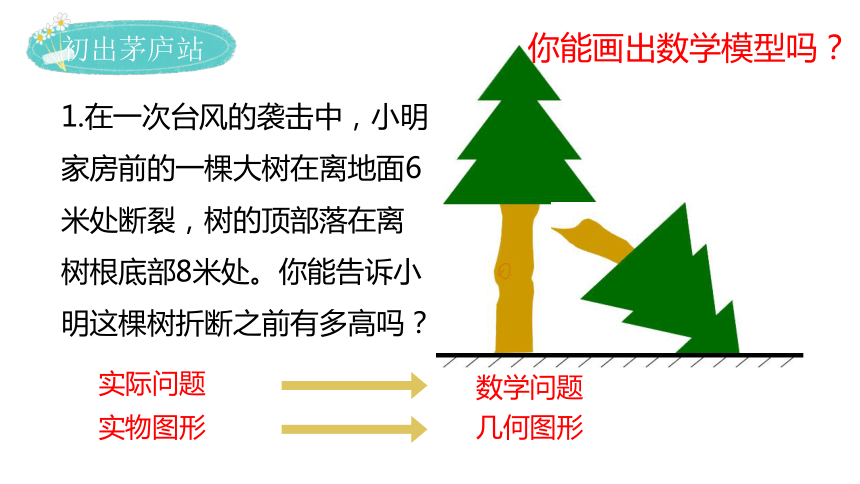
1.在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
初出茅庐站
实际问题
数学问题
实物图形
几何图形
你能画出数学模型吗?
初出茅庐站
建模思想
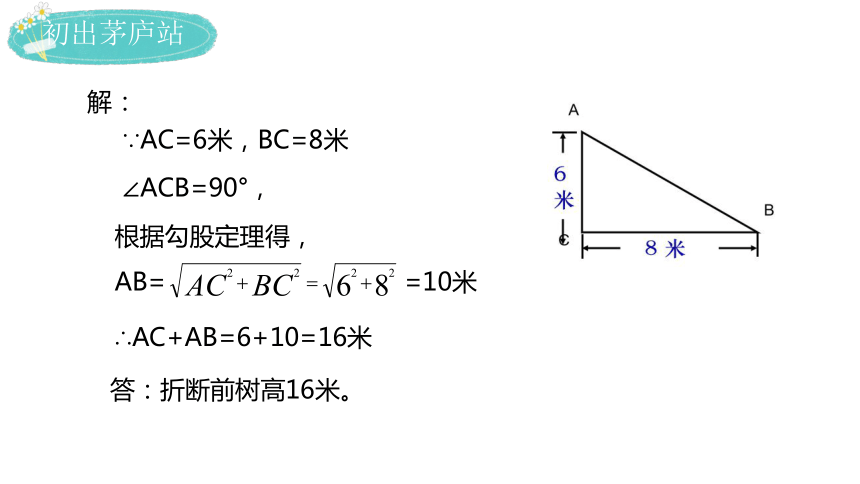
解:
∵AC=6米,BC=8米
∠ACB=90°,
根据勾股定理得,
∴AC+AB=6+10=16米
答:折断前树高16米。
初出茅庐站
AB= =10米
1
2
初出茅庐站
展露锋芒站
勾股应用之旅
2
展露锋芒站
2.如图,若该住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),已知AB⊥AD,AD=3m,AB=4m,CD=12m,BC=13m,试求这块空地的面积?
A
B
C
D
3
4
13
12
展露锋芒站
3.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2 .求证:AB//DC.
练一练
1
2
3
初出茅庐站
展露锋芒站
大展身手站
勾股应用之旅
3
大展身手站
湖中红莲露一尺,忽被强风吹一边,
花离原位三尺远,湖水如何知深浅?
A
D
1尺
3尺
?
∟
C
B
大展身手站
解:
∵AD=1尺,CD=3尺
设BD=x,则AB=x+1
∴BC=x+1
在Rt△BCD中,∠BDC=90°,
根据勾股定理得,
即,
解得,
x=4
答:水池的水深为4尺。
大展身手站
∟
1尺
3尺
x
x+1
x+1
通过本节课,你收获了什么?
课堂小结
1
2
3
初出茅庐站
展露锋芒站
大展身手站
∟
勾股应用之旅
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
当堂小测
2.一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1.5小时后,它们相距________海里。
30
当堂小测
3.一个矩形纸条ABCD,AD=9,AB=3,沿EF折叠,使点D和点B重合,点C与C’重合,则DE的长为__________。
A
B
C
D
E
F
C’
5
当堂小测
4.如图,有两棵树,一棵高8米,另一棵高2米,两棵树相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
当堂小测
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
当堂小测
如果变成钝角或锐角三角形,三边会有怎样的关系?
壹
贰
叁
走进生活,思考勾股定理的其他应用
课后作业与思考
必做题:p47页2、3、5题
选做题:p47页6题
课后作业
课后思考
勾股定理的应用
湖中红莲露一尺,忽被强风吹一边,
花离原位三尺远,湖水如何知深浅?
A
D
C
B
1
勾股应用之旅
初出茅庐站
1
初出茅庐站
1.在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
初出茅庐站
实际问题
数学问题
实物图形
几何图形
你能画出数学模型吗?
初出茅庐站
建模思想
解:
∵AC=6米,BC=8米
∠ACB=90°,
根据勾股定理得,
∴AC+AB=6+10=16米
答:折断前树高16米。
初出茅庐站
AB= =10米
1
2
初出茅庐站
展露锋芒站
勾股应用之旅
2
展露锋芒站
2.如图,若该住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),已知AB⊥AD,AD=3m,AB=4m,CD=12m,BC=13m,试求这块空地的面积?
A
B
C
D
3
4
13
12
展露锋芒站
3.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2 .求证:AB//DC.
练一练
1
2
3
初出茅庐站
展露锋芒站
大展身手站
勾股应用之旅
3
大展身手站
湖中红莲露一尺,忽被强风吹一边,
花离原位三尺远,湖水如何知深浅?
A
D
1尺
3尺
?
∟
C
B
大展身手站
解:
∵AD=1尺,CD=3尺
设BD=x,则AB=x+1
∴BC=x+1
在Rt△BCD中,∠BDC=90°,
根据勾股定理得,
即,
解得,
x=4
答:水池的水深为4尺。
大展身手站
∟
1尺
3尺
x
x+1
x+1
通过本节课,你收获了什么?
课堂小结
1
2
3
初出茅庐站
展露锋芒站
大展身手站
∟
勾股应用之旅
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
当堂小测
2.一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1.5小时后,它们相距________海里。
30
当堂小测
3.一个矩形纸条ABCD,AD=9,AB=3,沿EF折叠,使点D和点B重合,点C与C’重合,则DE的长为__________。
A
B
C
D
E
F
C’
5
当堂小测
4.如图,有两棵树,一棵高8米,另一棵高2米,两棵树相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
当堂小测
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
当堂小测
如果变成钝角或锐角三角形,三边会有怎样的关系?
壹
贰
叁
走进生活,思考勾股定理的其他应用
课后作业与思考
必做题:p47页2、3、5题
选做题:p47页6题
课后作业
课后思考
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
