人教版初中数学七年级上册5.1.1一元一次方程的定义(共22张PPT)
文档属性
| 名称 | 人教版初中数学七年级上册5.1.1一元一次方程的定义(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 15:48:51 | ||
图片预览






文档简介
(共22张PPT)
人教版初中数学七年级上册
临沂·新琅琊
教学内容解析
思想支持
架构依据
知识承托
学会用整体、联系、发展的眼光看待问题,发展核心素养.
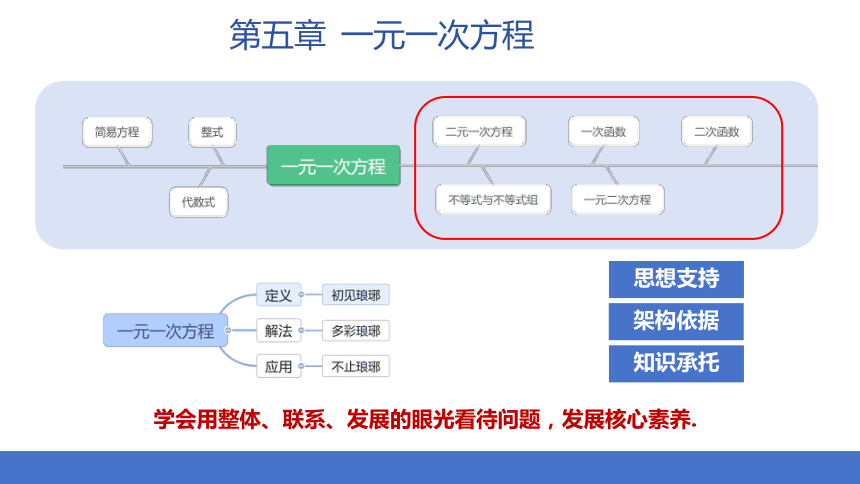
第五章 一元一次方程
学习目标
1、掌握方程的解的概念以及一元一次方程的定义,学会判断某个数值是不是一元一次方程的解.
2、根据问题寻找相等关系、根据相等关系列出方程的过程中,领悟一元一次方程的意义和作用,提升获取信息、分析问题、处理问题的能力;
3、经历把实际问题抽象为数学方程的过程,认识到方程是刻画现实世界的一种有效的数学模型,初步体会建立数学模型的思想;
沂州府衙
古典艺术
沂州商贸
琅琊盛世
琅琊秘境
琅琊大剧院
目标地
古典艺术
沂州商贸
2号营地
1号营地
大本营
任务1 感知模型
问题:
初见琅琊,甲、乙两支研学队沿同一条路线同时向一目标地进发,甲队从距大本营1km的1号营地出发,每小时行进2.8km;乙队从距大本营3km的2号营地出发,每小时行进0.8km.多长时间后,甲队在途中追上乙队
根据题意,你能列出方程吗?
解:设经过x小时,甲队追上乙队
2.8x+1
0.8x+3
=
任务1 可感知——模型构建
甲
乙
思考:请估算,多长时间后,甲队在途中追上乙队?
任务1 可感知——模型构建
甲速度 甲时间 甲距大本营的路程 乙速度 乙时间 乙距大本营的路程
2.8 x 0.8 x
2.8 0.1 0.8 0.1
2.8 0.5 0.8 0.5
2.8 …… 0.8 ……
2.8x+1
0.8x+3
=
2.8x+1
当x=1时,左边==
2.8x0.1+1=1.28
0.8x0.1+3=3.08
0.8x+3
左边=右边
一般地,使方程左、右两边的值相等的未知数的值,
叫做方程的解。
2.8x+1
0.8x+3 的解.
=
所以x=1就是方程
任务1 可感知——概念理解
学生活动 【一起归纳】
求方程解的过程,叫做解方程。
特殊
一般
当x=1时,左边==
任务2 能应用——深度学习
例:
(1)x=2,x=是方程2x=3的解吗?
(2)x=10,x=20是方程3x=4(x-5)的解吗?
解:
(1)当x=2时,方程2x=3的左边=2×2=4,右边=3,方程左、右两边的值不相等,所以x=2不是方程2x=3的解;
当x=时,方程2x=3的左边=2×=3,右边=3,方程左、右两边的值相等,所以x= 是方程2x=3的解;
(2)当x=10时,方程3x=4(x-5)的左边=3×10=30,右边=4×(10-5)=20,方程左、右两边的值不相等,所以x=10不是方程3x=4(x-5)的解;
当x=时,方程3x=4(x-5)的左边=3×20=60,右边= 4×(20-5)=60,方程左、右两边的值相等,所以x=20是方程3x=4(x-5)的解;
1. 将数值代入方程左边进行计算,
2. 将数值代入方程右边进行计算,
3. 判断左边=右边?相等,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
任务2 能应用——深度学习
学生活动 【一起归纳】
1左
2右
3判断
任务3 驱动模型
1、判断x=2和x=4是不是方程2x-3=5的解.
2、x=60是方程=4000的解吗?x=80呢?
请同学们按照例题中的方法,判断下列取值是否是方程的解.
对比:哪种方程更简单?
任务2 能应用——深度学习
你来我往:同桌,考考你!
任务3 善归纳——方程再探
思考 观察下列方程:
2x+1=0.8x+3
0.52x-(1-0.52)x=80
3x=4(x-5)
学生活动 【一起探究】
问题1 每个方程中,各含有几个未知数?
问题2 等号两边的式子有什么共同点?
问题3 说一说每个方程中未知数的次数.
1个
都是整式
1次
任务3 善归纳——方程再探
学生活动 【一起归纳】
这样的方程叫做一元一次方程.
(一次)
一般地,只含有一个未知数,
(一元)
且含有未知数的式子都是整式,
未知数的次数都是1,
任务4 自适应——知识迁移
下列哪些是一元一次方程?
(1) 2+3=3+2 ; (2) ;
(3) ; (4) ;
(5) ; (6) ;
(7) ; (8) 8y-9=9-y ;
√
√
+2x+1=4
学生活动 【一起应用】
=4000
如果不是,你能尝试给它们取名字吗?
若关于x的方程 是一元一次方程,则 n 的值为 .
【变式2】方程 是关于x的一元一次方程,则 n= .
2
归纳 一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;
②未知数的系数不为0.
学生活动
任务4 自适应——融会贯通
【一起归纳】
【变式1】若关于x的方程 是一元一次方程,则 n 的值为 .
2或-2
-2
任务5 外迁移——博古通今
在公元前1600年左右遗留下来的一卷古埃及纸草书中,记载着一些数学问题。其中一个问题翻译过来是:“啊哈,它的全部,它的 ,其和等于16。”你能求出问题中的“它”吗
解:设这个“它”为x,由题意可得:
x + x =16
你能得出方程的解吗?
实验中学球队参加足球联赛,规定每队胜一场得3分,平一场得1分,负一场得0分。该球队已比赛了10场,并保持不败,一共得了22分。该球队已胜了多少场 平了多少场
解:设该校女子足球队胜了x场,则平了(10-x)场,由题意可得:
3x +(10 -x) = 22
任务5 外迁移——联系实际
你能得出方程的解吗?
任务6 内自省——能力内化
2. 若 x =1是方程x2 -2mx +1=0的一个解,则m的值为( )
A. 0 B. 2 C. 1 D. -1
1. x =1是下列哪个方程的解 ( )
A. B. C. D.
B
C
巩固提高
3. 下列方程:
其中是方程的是 ,是一元一次方程的是 .(填序号)
①②③④⑤
②③
4. 根据下列问题,找出等量关系,设未知数列出方程,并指出其是不是一元一次方程.
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3000 m?
巩固提高
任务6 内自省——能力内化
(2)甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用 9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
(3)一个梯形的下底比上底多2 cm,高是5 cm,面积是40 cm2,求上底.
5. 已知方程 是关于x的一元一次方程,求m的值,并写出该方程.
解:设沿跑道跑x周.
400x=3000, 是一元一次方程.
解:设甲种铅笔买了x支,乙种铅笔买了(20-x)支.
0.3x+0.6(20-x)=9, 是一元一次方程.
解:设上底为x cm,则下底为(x+2)cm.
, 是一元一次方程.
解:因为方程 是关于x的一元
一次方程,
所以|m|-1 = 1,且m-2≠0,得m = -2.
所以原方程为-4x+3 = -7.
2.本节课在研究方程的解的过程中用到了哪些数学思想方法?
3.在本节课的学习过程中你还有其它方面的收获或疑惑吗?
4.依据本单元起始课得到的方程研究路径,接下来我们该继续研究一元一次方程的什么内容?
1.本节课主要研究了什么内容?具体研究路径是怎样的?
任务7 促升华——单元体系
一元一次方程单元知识结构体系
任务7 促升华——单元体系
分层作业
必做:教材115页练习1、2
选做:教材118页习题5.1第3题
任务8 挖潜力——课后巩固
谢
谢
观
看
人教版初中数学七年级上册
临沂·新琅琊
教学内容解析
思想支持
架构依据
知识承托
学会用整体、联系、发展的眼光看待问题,发展核心素养.
第五章 一元一次方程
学习目标
1、掌握方程的解的概念以及一元一次方程的定义,学会判断某个数值是不是一元一次方程的解.
2、根据问题寻找相等关系、根据相等关系列出方程的过程中,领悟一元一次方程的意义和作用,提升获取信息、分析问题、处理问题的能力;
3、经历把实际问题抽象为数学方程的过程,认识到方程是刻画现实世界的一种有效的数学模型,初步体会建立数学模型的思想;
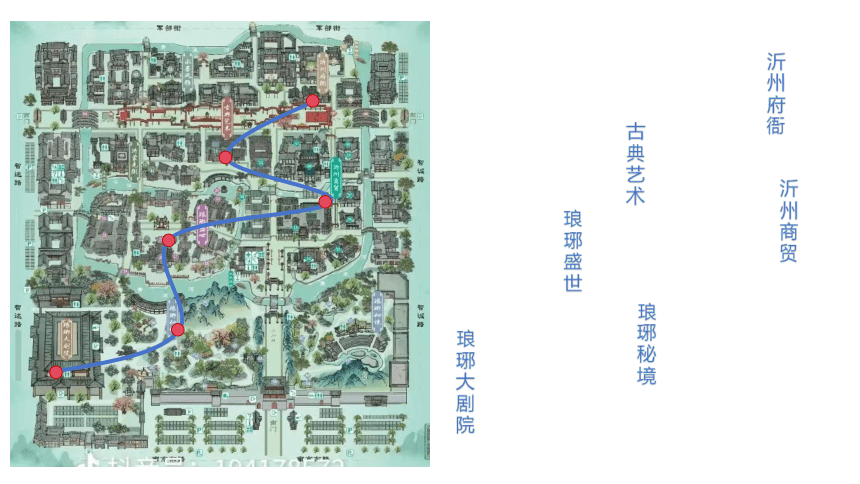
沂州府衙
古典艺术
沂州商贸
琅琊盛世
琅琊秘境
琅琊大剧院
目标地
古典艺术
沂州商贸
2号营地
1号营地
大本营
任务1 感知模型
问题:
初见琅琊,甲、乙两支研学队沿同一条路线同时向一目标地进发,甲队从距大本营1km的1号营地出发,每小时行进2.8km;乙队从距大本营3km的2号营地出发,每小时行进0.8km.多长时间后,甲队在途中追上乙队
根据题意,你能列出方程吗?
解:设经过x小时,甲队追上乙队
2.8x+1
0.8x+3
=
任务1 可感知——模型构建
甲
乙
思考:请估算,多长时间后,甲队在途中追上乙队?
任务1 可感知——模型构建
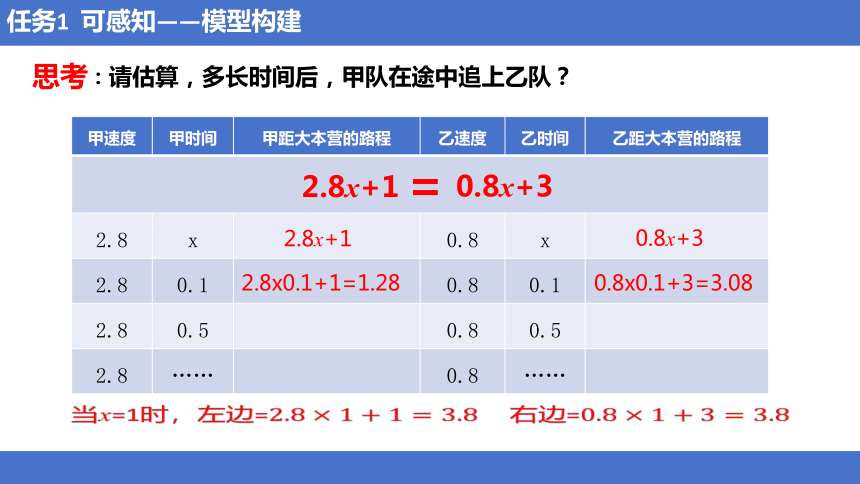
甲速度 甲时间 甲距大本营的路程 乙速度 乙时间 乙距大本营的路程
2.8 x 0.8 x
2.8 0.1 0.8 0.1
2.8 0.5 0.8 0.5
2.8 …… 0.8 ……
2.8x+1
0.8x+3
=
2.8x+1
当x=1时,左边==
2.8x0.1+1=1.28
0.8x0.1+3=3.08
0.8x+3
左边=右边
一般地,使方程左、右两边的值相等的未知数的值,
叫做方程的解。
2.8x+1
0.8x+3 的解.
=
所以x=1就是方程
任务1 可感知——概念理解
学生活动 【一起归纳】
求方程解的过程,叫做解方程。
特殊
一般
当x=1时,左边==
任务2 能应用——深度学习
例:
(1)x=2,x=是方程2x=3的解吗?
(2)x=10,x=20是方程3x=4(x-5)的解吗?
解:
(1)当x=2时,方程2x=3的左边=2×2=4,右边=3,方程左、右两边的值不相等,所以x=2不是方程2x=3的解;
当x=时,方程2x=3的左边=2×=3,右边=3,方程左、右两边的值相等,所以x= 是方程2x=3的解;
(2)当x=10时,方程3x=4(x-5)的左边=3×10=30,右边=4×(10-5)=20,方程左、右两边的值不相等,所以x=10不是方程3x=4(x-5)的解;
当x=时,方程3x=4(x-5)的左边=3×20=60,右边= 4×(20-5)=60,方程左、右两边的值相等,所以x=20是方程3x=4(x-5)的解;
1. 将数值代入方程左边进行计算,
2. 将数值代入方程右边进行计算,
3. 判断左边=右边?相等,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
任务2 能应用——深度学习
学生活动 【一起归纳】
1左
2右
3判断
任务3 驱动模型
1、判断x=2和x=4是不是方程2x-3=5的解.
2、x=60是方程=4000的解吗?x=80呢?
请同学们按照例题中的方法,判断下列取值是否是方程的解.
对比:哪种方程更简单?
任务2 能应用——深度学习
你来我往:同桌,考考你!
任务3 善归纳——方程再探
思考 观察下列方程:
2x+1=0.8x+3
0.52x-(1-0.52)x=80
3x=4(x-5)
学生活动 【一起探究】
问题1 每个方程中,各含有几个未知数?
问题2 等号两边的式子有什么共同点?
问题3 说一说每个方程中未知数的次数.
1个
都是整式
1次
任务3 善归纳——方程再探
学生活动 【一起归纳】
这样的方程叫做一元一次方程.
(一次)
一般地,只含有一个未知数,
(一元)
且含有未知数的式子都是整式,
未知数的次数都是1,
任务4 自适应——知识迁移
下列哪些是一元一次方程?
(1) 2+3=3+2 ; (2) ;
(3) ; (4) ;
(5) ; (6) ;
(7) ; (8) 8y-9=9-y ;
√
√
+2x+1=4
学生活动 【一起应用】
=4000
如果不是,你能尝试给它们取名字吗?
若关于x的方程 是一元一次方程,则 n 的值为 .
【变式2】方程 是关于x的一元一次方程,则 n= .
2
归纳 一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;
②未知数的系数不为0.
学生活动
任务4 自适应——融会贯通
【一起归纳】
【变式1】若关于x的方程 是一元一次方程,则 n 的值为 .
2或-2
-2
任务5 外迁移——博古通今
在公元前1600年左右遗留下来的一卷古埃及纸草书中,记载着一些数学问题。其中一个问题翻译过来是:“啊哈,它的全部,它的 ,其和等于16。”你能求出问题中的“它”吗
解:设这个“它”为x,由题意可得:
x + x =16
你能得出方程的解吗?
实验中学球队参加足球联赛,规定每队胜一场得3分,平一场得1分,负一场得0分。该球队已比赛了10场,并保持不败,一共得了22分。该球队已胜了多少场 平了多少场
解:设该校女子足球队胜了x场,则平了(10-x)场,由题意可得:
3x +(10 -x) = 22
任务5 外迁移——联系实际
你能得出方程的解吗?
任务6 内自省——能力内化
2. 若 x =1是方程x2 -2mx +1=0的一个解,则m的值为( )
A. 0 B. 2 C. 1 D. -1
1. x =1是下列哪个方程的解 ( )
A. B. C. D.
B
C
巩固提高
3. 下列方程:
其中是方程的是 ,是一元一次方程的是 .(填序号)
①②③④⑤
②③
4. 根据下列问题,找出等量关系,设未知数列出方程,并指出其是不是一元一次方程.
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3000 m?
巩固提高
任务6 内自省——能力内化
(2)甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用 9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
(3)一个梯形的下底比上底多2 cm,高是5 cm,面积是40 cm2,求上底.
5. 已知方程 是关于x的一元一次方程,求m的值,并写出该方程.
解:设沿跑道跑x周.
400x=3000, 是一元一次方程.
解:设甲种铅笔买了x支,乙种铅笔买了(20-x)支.
0.3x+0.6(20-x)=9, 是一元一次方程.
解:设上底为x cm,则下底为(x+2)cm.
, 是一元一次方程.
解:因为方程 是关于x的一元
一次方程,
所以|m|-1 = 1,且m-2≠0,得m = -2.
所以原方程为-4x+3 = -7.
2.本节课在研究方程的解的过程中用到了哪些数学思想方法?
3.在本节课的学习过程中你还有其它方面的收获或疑惑吗?
4.依据本单元起始课得到的方程研究路径,接下来我们该继续研究一元一次方程的什么内容?
1.本节课主要研究了什么内容?具体研究路径是怎样的?
任务7 促升华——单元体系
一元一次方程单元知识结构体系
任务7 促升华——单元体系
分层作业
必做:教材115页练习1、2
选做:教材118页习题5.1第3题
任务8 挖潜力——课后巩固
谢
谢
观
看
同课章节目录
