七年级上册数学鲁教版 3.1.1 探索勾股定理 课件(共21张PPT)
文档属性
| 名称 | 七年级上册数学鲁教版 3.1.1 探索勾股定理 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
直角三角形
勾股定理
勾股定理逆定理
勾股定理的应用
单元概述
a
c
b
三角形
探究三角形全等
轴对称
等腰三角形
边 角
第三章 勾股定理
1 探索勾股定理
1、经历勾股定理的探究过程,知道勾股定理的内容,会初步运用勾股定理进行简单计算,会用数学眼光观察世界。
2、学生经历“观察—猜想—归纳—验证”的数学过程,发展数形结合和由特殊到一般的数学思想,会用数学语言表达世界。
3、 在探究活动中,学生感受数学文化的价值,引导学生欣赏与发现数学之美,体验解决问题方法的多样性,培养合作交流意识和探究精神,会用数学思维思考世界。
学习目标
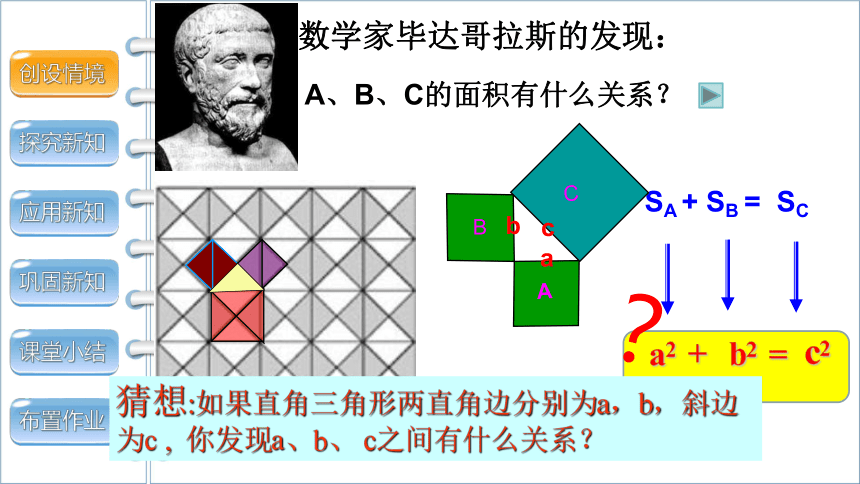
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
SA + SB = SC
A
B
C
a2
+
b2
=
c2
a
b
c
猜想:如果直角三角形两直角边分别为a,b,斜边为c , 你发现a、b、 c之间有什么关系?
?
(1)在纸上作出1个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系?与同伴交流(小组讨论)
a b c 可能的关系
要求:一人画直角三角形并测量,另外三人分别计算边长平方
探究一
我会测
A
B
C
图1
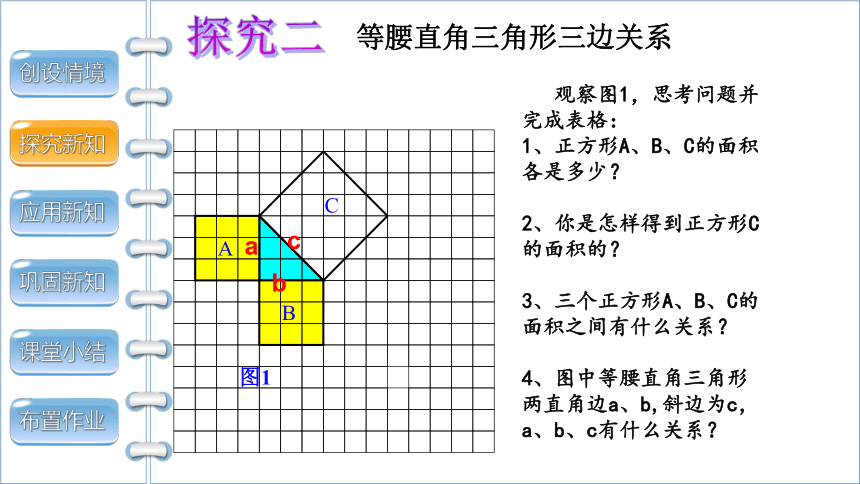
等腰直角三角形三边关系
探究二
a
b
c
观察图1,思考问题并完成表格:
1、正方形A、B、C的面积各是多少?
2、你是怎样得到正方形C的面积的?
3、三个正方形A、B、C的面积之间有什么关系?
4、图中等腰直角三角形两直角边a、b,斜边为c,a、b、c有什么关系?
图1
A的面积
B的面积
C的面积
面积之间的关系
a、b、c之间的关系
A
B
C
图1
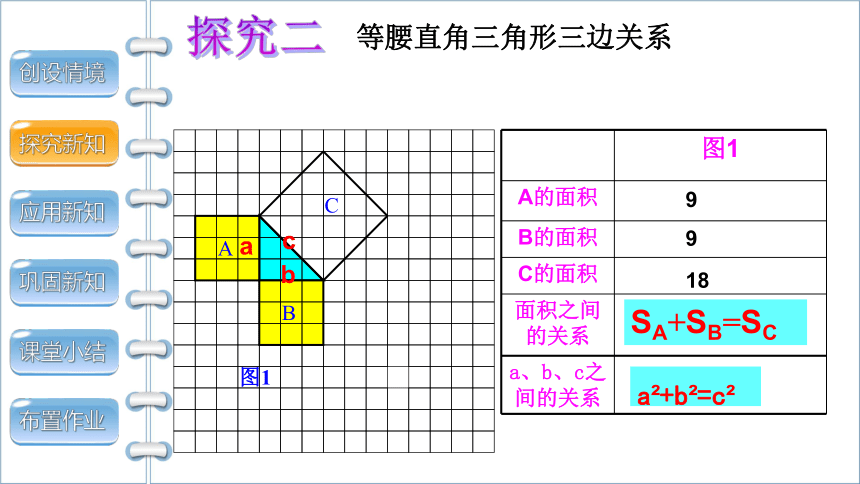
等腰直角三角形三边关系
探究二
SA+SB=SC
a
b
c
a +b =c
9
9
18
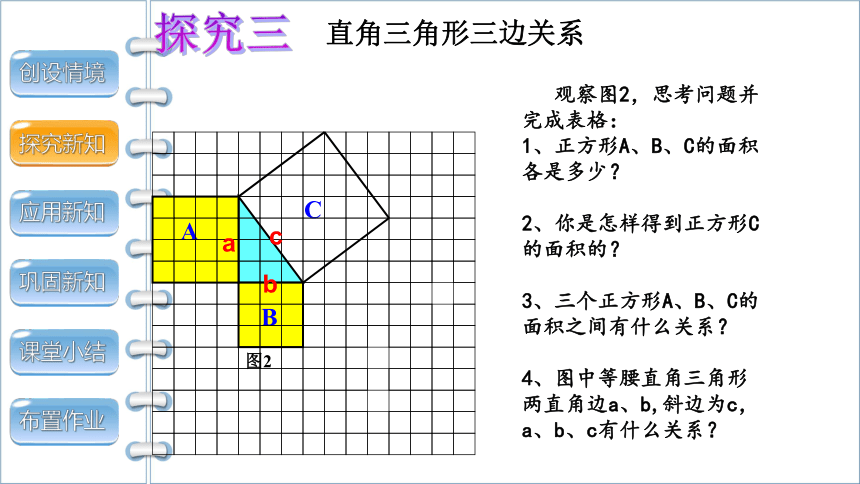
探究三
直角三角形三边关系
A
B
C
图2
a
b
c
观察图2,思考问题并完成表格:
1、正方形A、B、C的面积各是多少?
2、你是怎样得到正方形C的面积的?
3、三个正方形A、B、C的面积之间有什么关系?
4、图中等腰直角三角形两直角边a、b,斜边为c,a、b、c有什么关系?
图2
A的面积
B的面积
C的面积
面积之间的关系
a、b、c之间的关系
探究三
直角三角形三边关系
A
B
C
图3
16
9
25
a
b
c
SA+SB=SC
a +b =c
对于一般直角三角形是否也有这个发现的呢?
几何画板演示
想一想:
1.成立条件: 在直角三角形中;
作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
a
b
c
直角三角形直角边的平方和等于斜边的平方。如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
a
=c -b
b
=c -a
评价等级 A(☆☆☆☆☆) B(☆☆☆) C(☆☆)
评价指标 合作探究能力 动手操作能力 语言表达能力
①成员分工明确☆☆ ②最先完成数据收集☆ ③找出直角三角形三边关系☆ ④能用文字和符号语言说出勾股定理☆ ①快速找出直角三角形三边关系☆☆ ②能用文字或符号语言说出勾股定理☆ 积极上台展示,能准确表达探究的过程☆☆
自评
星级评价
1.求下图中字母所代表的正方形的面积:
跟踪训练
例 在Rt△ABC中,∠C=90°,
AC=4cm,BC=3cm,求AB的长度。
A
B
C
解:在Rt△ABC中
AC +BC =AB
∵ AC=4cm BC=3cm
∴ AB =4 +3
AB =16+9
AB =25
∴ AB=5cm
跟踪训练
1、在Rt△ABC中,
∠C=90°
(1)若AC=6,BC=8,求AB ;
(2)若AB=5,AC=3,求BC 。
A
B
C
变式训练
回归教材
如图,从电线杆离地面8m处向地面拉一条钢索,若这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
8 m
6 m
勾股定理
数学思想
由特殊到一般
数形结合
分类讨论
勾股定理
知识点
应用
探究经验
观察-猜想-归纳-验证
数学方法
割补法
测量
数格子
评价等级 A(☆☆☆☆) B(☆☆☆) C(☆☆)
评价指标 ①正确运用勾股定理求得运算结果☆☆ ②计算正确,步骤严谨,书写规范☆☆ ①准确求得运算结果☆ ②计算正确,步骤严谨,书写欠规范☆☆ 积极上台展示,能准确表达探究的过程☆☆
自评
星级评价
当堂检测
1、判断题
(1)在直角三角形中,若勾为3,股为4,则弦为5。 ( )
(2)直角三角形两边的平方和等于第三边的平方。 ( )
(3)在Rt△ABC中,∠B=90°,则。 ( )
√
×
×
3、已知:Rt△ABC中,AB=4,AC=3,则BC2的长为___________
当堂检测
25或7
2、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A. 2、4、6; B. 6、8、10;
C. 4、6、8; D. 8、10、12.
B
4、已知:在△ABC中,AB=AC=17,
BD=DC=8,则高AD=___,
S△ABC=__
15
120
当堂检测
直角三角形
勾股定理
勾股定理逆定理
勾股定理的应用
单元概述
a
c
b
三角形
探究三角形全等
轴对称
等腰三角形
边 角
第三章 勾股定理
1 探索勾股定理
1、经历勾股定理的探究过程,知道勾股定理的内容,会初步运用勾股定理进行简单计算,会用数学眼光观察世界。
2、学生经历“观察—猜想—归纳—验证”的数学过程,发展数形结合和由特殊到一般的数学思想,会用数学语言表达世界。
3、 在探究活动中,学生感受数学文化的价值,引导学生欣赏与发现数学之美,体验解决问题方法的多样性,培养合作交流意识和探究精神,会用数学思维思考世界。
学习目标
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
SA + SB = SC
A
B
C
a2
+
b2
=
c2
a
b
c
猜想:如果直角三角形两直角边分别为a,b,斜边为c , 你发现a、b、 c之间有什么关系?
?
(1)在纸上作出1个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系?与同伴交流(小组讨论)
a b c 可能的关系
要求:一人画直角三角形并测量,另外三人分别计算边长平方
探究一
我会测
A
B
C
图1
等腰直角三角形三边关系
探究二
a
b
c
观察图1,思考问题并完成表格:
1、正方形A、B、C的面积各是多少?
2、你是怎样得到正方形C的面积的?
3、三个正方形A、B、C的面积之间有什么关系?
4、图中等腰直角三角形两直角边a、b,斜边为c,a、b、c有什么关系?
图1
A的面积
B的面积
C的面积
面积之间的关系
a、b、c之间的关系
A
B
C
图1
等腰直角三角形三边关系
探究二
SA+SB=SC
a
b
c
a +b =c
9
9
18
探究三
直角三角形三边关系
A
B
C
图2
a
b
c
观察图2,思考问题并完成表格:
1、正方形A、B、C的面积各是多少?
2、你是怎样得到正方形C的面积的?
3、三个正方形A、B、C的面积之间有什么关系?
4、图中等腰直角三角形两直角边a、b,斜边为c,a、b、c有什么关系?
图2
A的面积
B的面积
C的面积
面积之间的关系
a、b、c之间的关系
探究三
直角三角形三边关系
A
B
C
图3
16
9
25
a
b
c
SA+SB=SC
a +b =c
对于一般直角三角形是否也有这个发现的呢?
几何画板演示
想一想:
1.成立条件: 在直角三角形中;
作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
a
b
c
直角三角形直角边的平方和等于斜边的平方。如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
a
=c -b
b
=c -a
评价等级 A(☆☆☆☆☆) B(☆☆☆) C(☆☆)
评价指标 合作探究能力 动手操作能力 语言表达能力
①成员分工明确☆☆ ②最先完成数据收集☆ ③找出直角三角形三边关系☆ ④能用文字和符号语言说出勾股定理☆ ①快速找出直角三角形三边关系☆☆ ②能用文字或符号语言说出勾股定理☆ 积极上台展示,能准确表达探究的过程☆☆
自评
星级评价
1.求下图中字母所代表的正方形的面积:
跟踪训练
例 在Rt△ABC中,∠C=90°,
AC=4cm,BC=3cm,求AB的长度。
A
B
C
解:在Rt△ABC中
AC +BC =AB
∵ AC=4cm BC=3cm
∴ AB =4 +3
AB =16+9
AB =25
∴ AB=5cm
跟踪训练
1、在Rt△ABC中,
∠C=90°
(1)若AC=6,BC=8,求AB ;
(2)若AB=5,AC=3,求BC 。
A
B
C
变式训练
回归教材
如图,从电线杆离地面8m处向地面拉一条钢索,若这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
8 m
6 m
勾股定理
数学思想
由特殊到一般
数形结合
分类讨论
勾股定理
知识点
应用
探究经验
观察-猜想-归纳-验证
数学方法
割补法
测量
数格子
评价等级 A(☆☆☆☆) B(☆☆☆) C(☆☆)
评价指标 ①正确运用勾股定理求得运算结果☆☆ ②计算正确,步骤严谨,书写规范☆☆ ①准确求得运算结果☆ ②计算正确,步骤严谨,书写欠规范☆☆ 积极上台展示,能准确表达探究的过程☆☆
自评
星级评价
当堂检测
1、判断题
(1)在直角三角形中,若勾为3,股为4,则弦为5。 ( )
(2)直角三角形两边的平方和等于第三边的平方。 ( )
(3)在Rt△ABC中,∠B=90°,则。 ( )
√
×
×
3、已知:Rt△ABC中,AB=4,AC=3,则BC2的长为___________
当堂检测
25或7
2、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A. 2、4、6; B. 6、8、10;
C. 4、6、8; D. 8、10、12.
B
4、已知:在△ABC中,AB=AC=17,
BD=DC=8,则高AD=___,
S△ABC=__
15
120
当堂检测
