青岛版九年级上册1.1相似多边形 课件(共25张PPT)
文档属性
| 名称 | 青岛版九年级上册1.1相似多边形 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 15:00:56 | ||
图片预览







文档简介
(共25张PPT)
初中数学 九年级上册 青岛出版社
《图形的相似》之
1.1 相似多边形
1.通过实例认识图形的相似;知道全等形与相似形的联系和区别,了解相似多边形和相似比;
2.能识别两个相似多边形的对应顶点、对应角和对应边,会求相似多边形的相似比;
3.会用符号表示相似多边形及它们的对应元素,写出对应边之间的比例式,发展符号意识。
学习目标
交流与发现
五星红旗是中华人民共和国的国旗。国旗上的左上角有五颗五角星。这五颗五角星的形状相同吗 大小相等吗
形状相同,
大小不一定相等。
导入新知—用数学眼光看奥运
形状相同的平面图形叫做相似形。
定义:
在生活中,你还见过哪些形状相同但大小未必相等的图形?
赢
赢
知识点1:
自主学习
相似形的定义。
大小 不一定 相等
探究一:全等形和相似形有什么关系呢?
智慧碰撞
两个全等形也是相似形。
两个相似形未必是全等形。
相似形
全等形
探究一:全等形和相似形有什么关系呢?
智慧碰撞
智慧碰撞
探究二:在电脑上任意画出一个四边形ABCD(图①),按原大小复制下来,得到四边形A′B′C′D′(图②)。然后将四边形ABCD各角的大小保持不变,将它的各边同时放大 倍,得到四边形A′′B′′C′′D′′(图③),再将四边形ABCD各角的大小保持不变,将它的各边同时缩小 ,得到四边形A′′′B′′′C′′′D′′′(图④),把这四个四边形打印在同一张纸上。
智慧碰撞
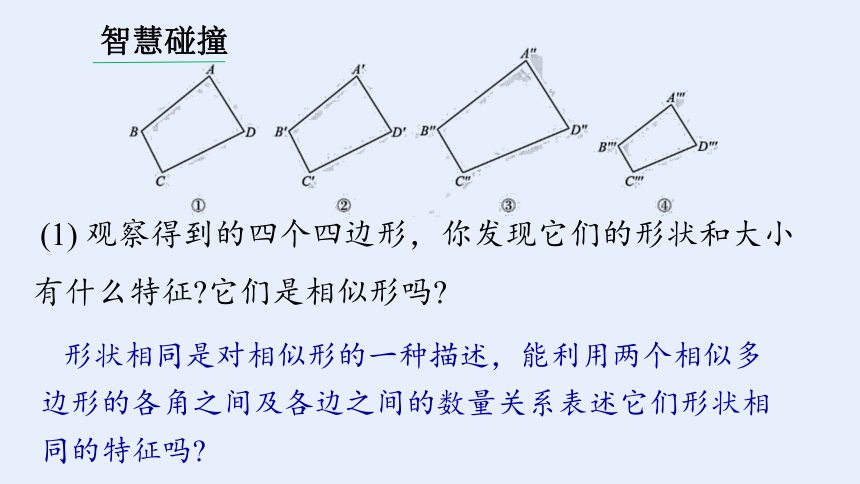
(1) 观察得到的四个四边形,你发现它们的形状和大小有什么特征 它们是相似形吗
形状相同是对相似形的一种描述,能利用两个相似多边形的各角之间及各边之间的数量关系表述它们形状相同的特征吗
智慧碰撞
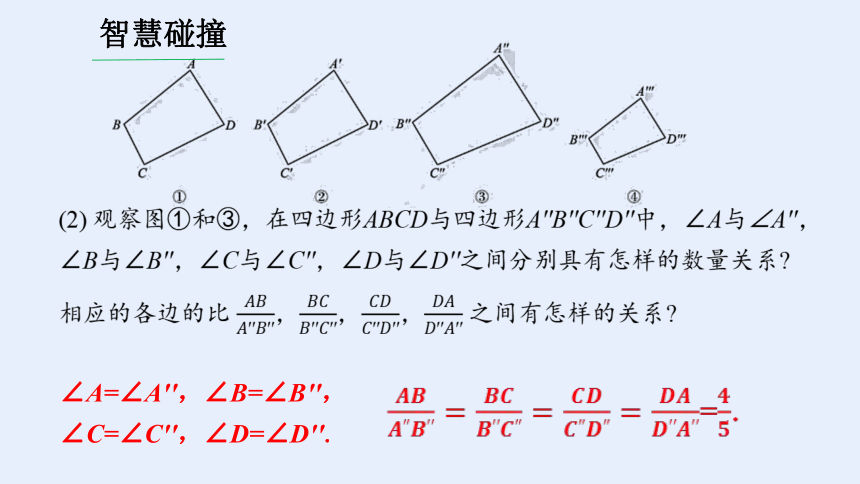
(2) 观察图①和③,在四边形ABCD与四边形A′′B′′C′′D′′中,∠A与∠A′′,∠B与∠B′′,∠C与∠C′′,∠D与∠D′′之间分别具有怎样的数量关系 相应的各边的比 ,,, 之间有怎样的关系
∠A=∠A′′,∠B=∠B′′,
∠C=∠C′′,∠D=∠D′′.
(3) 观察图①和④,四边形ABCD与四边形A′′′B′′′C′′′D′′′相应的各角及相应的各边分别具有怎样的数量关系 图③和图④呢
∠A=∠A′′′,∠B=∠B′′′,
∠C=∠C′′′,∠D=∠D′′′.
智慧碰撞
归纳总结:
把四边形ABCD复制、放大、或缩小后,所得到的四边形与原来的四边形_____。它们的各个角_________,各边___________。
相似
对应相等
对应成比例
反过来,如果一个四边形与四边形ABCD的各角对应相等,且各边对应成比例,那么这个四边形与四边形ABCD形状_____。
也就是说,这个四边形与四边形ABCD _______。
相同
相似
由此,你可以给出相似多边形的定义吗?
相似多边形的定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等,各边对应成比例,那么这两个多边形叫做相似多边形。
知识点2:
相似多边形的定义。
相似通常用符号“∽”表示,读作“相似于”,那么四边形ABCD和四边形A′B′C′D′ 相似,
记作:四边形ABCD∽四边形A′B′C′D′,
读作:四边形ABCD相似于四边形A′B′C′D′。
≌
形状相同
大小相等
针对性练习一
1.三角形与四边形能相似吗?等边三角形与直角三角形能相似吗?
2.如图,矩形的草坪长20m,宽10m,沿草坪四周外围有1m的环行小路,小路的内外边缘所成的矩形相似吗?
相似多边形对应边的比叫做相似比。
当两个多边形全等时,其相似比为____。
1
反之,如果两个相似多边形的相似比为1,那么这两个多边形_____。
全等
例如,我们前面得到四边形ABCD与四边形A′B′C′D′的相似比为 ,或说成4:5。
知识点3:
相似比的定义。
3.若△ABC ∽△A′B′C′,且AB∶A′B′=2∶3。
则△ABC 与△ A′B′C′相似比是 ,
△ A′B′C′与△ABC的相似比是 。
针对性练习二
2:3
3:2
例1.如图,已知四边形AEFD∽四边形EBCF。
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC的长。
A
D
E
F
B
C
典例精析
例1.如图,已知四边形AEFD∽四边形EBCF。
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC的长。
A
D
E
F
B
C
4. 如图,四边形ABCD∽四边形EFGH,求∠α、∠β 的大小和EH的长度。
解:∵四边形ABCD∽四边形EFGH,
∴∠α=∠C=83°,∠A=∠E=118°,
在四边形EFGH中,
∠β=360°-83°-78°-118°=81°,
∵四边形ABCD∽四边形EFGH,
∴EH:AD=EF:AB
∴x:21=24:18
解得x=28
针对性练习三
答:∠α=83°,∠β=81°,EH的长度是28cm。
同学们谈谈本节课你有哪些收获?
我知道了……
我学会了……
我能解决……
我获得的数学方法是……
智慧盘点
相似多边形
相似形VS全等形
相似多边形
定义
表示方法
③各边对应成比例
①边数相同
②各个角对应相等
相似比
智慧盘点
1. 下列图形不是相似形的是( )
A. 用同一底版打印出来的两张大小不等的照片
B. 原图案和用放大镜放大后的图案
C. 某人的侧面照片和正面照片
D. 大小不等的两张同版本的中国地图
2. 下列说法正确的是( )
A. 有一个角等于100°的两个等腰三角形相似
B. 两个矩形一定相似
C. 有一个角等于45°的两个等腰三角形相似
D. 相似三角形一定不是全等三角形
当堂检测
C
A
3.五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3,
(1)若∠D=135°,则∠D′= ______。
(2)若A′B′=15cm,则AB= ______。
4.一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______ 。
135°
当堂检测
5cm
18
5.【链接中考】把矩形ABCD 对折,折痕为EF,
若矩形ABCD ∽矩形EABF,AB=2,求BC。
解:∵矩形ABCD ∽矩形EABF
∴ =
∴AB =AE·BC
由题意可知AE= BC,AB=2
∴2 = BC
解得BC=2
发扬奥运精神,探寻数学新知!
初中数学 九年级上册 青岛出版社
《图形的相似》之
1.1 相似多边形
1.通过实例认识图形的相似;知道全等形与相似形的联系和区别,了解相似多边形和相似比;
2.能识别两个相似多边形的对应顶点、对应角和对应边,会求相似多边形的相似比;
3.会用符号表示相似多边形及它们的对应元素,写出对应边之间的比例式,发展符号意识。
学习目标
交流与发现
五星红旗是中华人民共和国的国旗。国旗上的左上角有五颗五角星。这五颗五角星的形状相同吗 大小相等吗
形状相同,
大小不一定相等。
导入新知—用数学眼光看奥运
形状相同的平面图形叫做相似形。
定义:
在生活中,你还见过哪些形状相同但大小未必相等的图形?
赢
赢
知识点1:
自主学习
相似形的定义。
大小 不一定 相等
探究一:全等形和相似形有什么关系呢?
智慧碰撞
两个全等形也是相似形。
两个相似形未必是全等形。
相似形
全等形
探究一:全等形和相似形有什么关系呢?
智慧碰撞
智慧碰撞
探究二:在电脑上任意画出一个四边形ABCD(图①),按原大小复制下来,得到四边形A′B′C′D′(图②)。然后将四边形ABCD各角的大小保持不变,将它的各边同时放大 倍,得到四边形A′′B′′C′′D′′(图③),再将四边形ABCD各角的大小保持不变,将它的各边同时缩小 ,得到四边形A′′′B′′′C′′′D′′′(图④),把这四个四边形打印在同一张纸上。
智慧碰撞
(1) 观察得到的四个四边形,你发现它们的形状和大小有什么特征 它们是相似形吗
形状相同是对相似形的一种描述,能利用两个相似多边形的各角之间及各边之间的数量关系表述它们形状相同的特征吗
智慧碰撞
(2) 观察图①和③,在四边形ABCD与四边形A′′B′′C′′D′′中,∠A与∠A′′,∠B与∠B′′,∠C与∠C′′,∠D与∠D′′之间分别具有怎样的数量关系 相应的各边的比 ,,, 之间有怎样的关系
∠A=∠A′′,∠B=∠B′′,
∠C=∠C′′,∠D=∠D′′.
(3) 观察图①和④,四边形ABCD与四边形A′′′B′′′C′′′D′′′相应的各角及相应的各边分别具有怎样的数量关系 图③和图④呢
∠A=∠A′′′,∠B=∠B′′′,
∠C=∠C′′′,∠D=∠D′′′.
智慧碰撞
归纳总结:
把四边形ABCD复制、放大、或缩小后,所得到的四边形与原来的四边形_____。它们的各个角_________,各边___________。
相似
对应相等
对应成比例
反过来,如果一个四边形与四边形ABCD的各角对应相等,且各边对应成比例,那么这个四边形与四边形ABCD形状_____。
也就是说,这个四边形与四边形ABCD _______。
相同
相似
由此,你可以给出相似多边形的定义吗?
相似多边形的定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等,各边对应成比例,那么这两个多边形叫做相似多边形。
知识点2:
相似多边形的定义。
相似通常用符号“∽”表示,读作“相似于”,那么四边形ABCD和四边形A′B′C′D′ 相似,
记作:四边形ABCD∽四边形A′B′C′D′,
读作:四边形ABCD相似于四边形A′B′C′D′。
≌
形状相同
大小相等
针对性练习一
1.三角形与四边形能相似吗?等边三角形与直角三角形能相似吗?
2.如图,矩形的草坪长20m,宽10m,沿草坪四周外围有1m的环行小路,小路的内外边缘所成的矩形相似吗?
相似多边形对应边的比叫做相似比。
当两个多边形全等时,其相似比为____。
1
反之,如果两个相似多边形的相似比为1,那么这两个多边形_____。
全等
例如,我们前面得到四边形ABCD与四边形A′B′C′D′的相似比为 ,或说成4:5。
知识点3:
相似比的定义。
3.若△ABC ∽△A′B′C′,且AB∶A′B′=2∶3。
则△ABC 与△ A′B′C′相似比是 ,
△ A′B′C′与△ABC的相似比是 。
针对性练习二
2:3
3:2
例1.如图,已知四边形AEFD∽四边形EBCF。
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC的长。
A
D
E
F
B
C
典例精析
例1.如图,已知四边形AEFD∽四边形EBCF。
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC的长。
A
D
E
F
B
C
4. 如图,四边形ABCD∽四边形EFGH,求∠α、∠β 的大小和EH的长度。
解:∵四边形ABCD∽四边形EFGH,
∴∠α=∠C=83°,∠A=∠E=118°,
在四边形EFGH中,
∠β=360°-83°-78°-118°=81°,
∵四边形ABCD∽四边形EFGH,
∴EH:AD=EF:AB
∴x:21=24:18
解得x=28
针对性练习三
答:∠α=83°,∠β=81°,EH的长度是28cm。
同学们谈谈本节课你有哪些收获?
我知道了……
我学会了……
我能解决……
我获得的数学方法是……
智慧盘点
相似多边形
相似形VS全等形
相似多边形
定义
表示方法
③各边对应成比例
①边数相同
②各个角对应相等
相似比
智慧盘点
1. 下列图形不是相似形的是( )
A. 用同一底版打印出来的两张大小不等的照片
B. 原图案和用放大镜放大后的图案
C. 某人的侧面照片和正面照片
D. 大小不等的两张同版本的中国地图
2. 下列说法正确的是( )
A. 有一个角等于100°的两个等腰三角形相似
B. 两个矩形一定相似
C. 有一个角等于45°的两个等腰三角形相似
D. 相似三角形一定不是全等三角形
当堂检测
C
A
3.五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3,
(1)若∠D=135°,则∠D′= ______。
(2)若A′B′=15cm,则AB= ______。
4.一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______ 。
135°
当堂检测
5cm
18
5.【链接中考】把矩形ABCD 对折,折痕为EF,
若矩形ABCD ∽矩形EABF,AB=2,求BC。
解:∵矩形ABCD ∽矩形EABF
∴ =
∴AB =AE·BC
由题意可知AE= BC,AB=2
∴2 = BC
解得BC=2
发扬奥运精神,探寻数学新知!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
