第五章 位置与坐标 章末复习(含答案)
文档属性
| 名称 | 第五章 位置与坐标 章末复习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 14.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 09:13:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 位置与坐标
章末复习
类型一 确定位置
1.下列数据中不能确定物体位置的是 ( )
A.电影票上的“5排8号” B.小明住在某小区3号楼7号
C.南偏西 D.东经 北纬 的城市
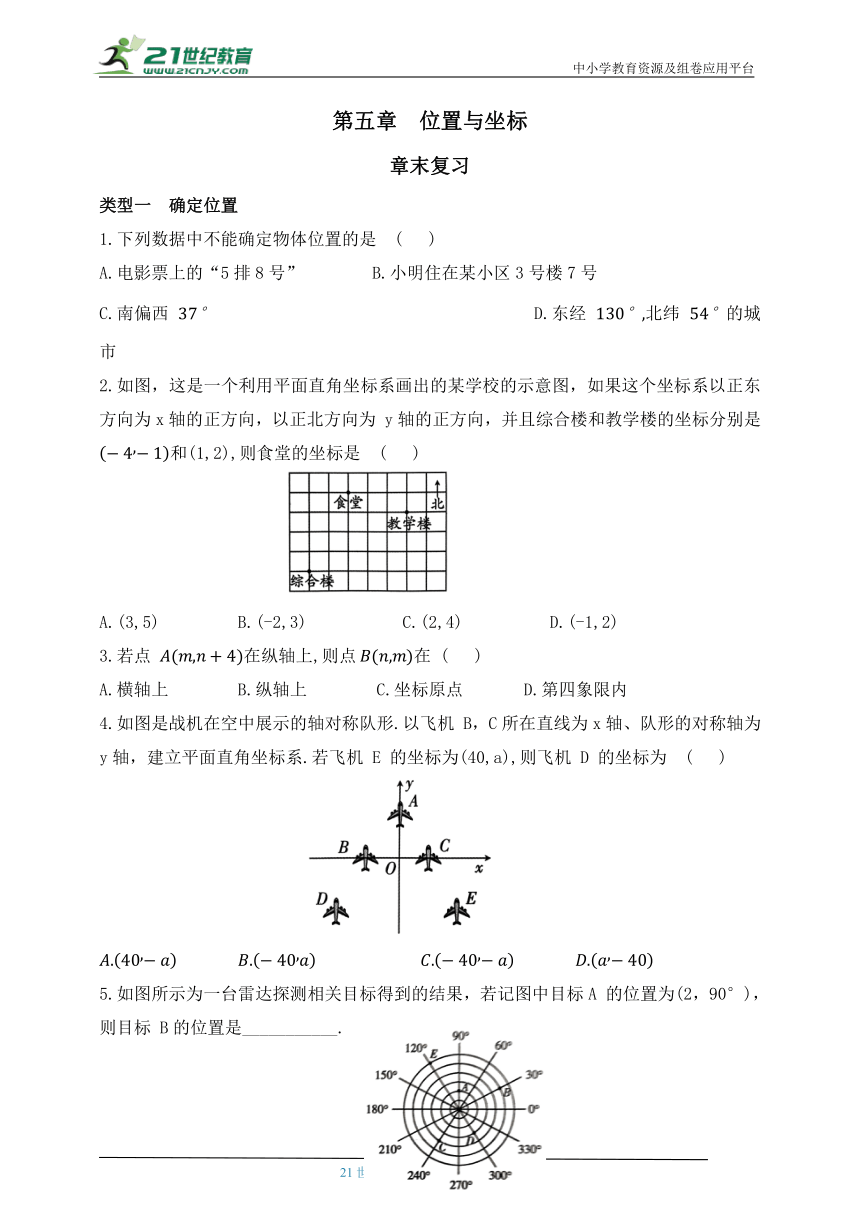
2.如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系以正东方向为x轴的正方向,以正北方向为 y轴的正方向,并且综合楼和教学楼的坐标分别是 和(1,2),则食堂的坐标是 ( )
A.(3,5) B.(-2,3) C.(2,4) D.(-1,2)
3.若点 在纵轴上,则点在 ( )
A.横轴上 B.纵轴上 C.坐标原点 D.第四象限内
4.如图是战机在空中展示的轴对称队形.以飞机 B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机 E 的坐标为(40,a),则飞机 D 的坐标为 ( )
5.如图所示为一台雷达探测相关目标得到的结果,若记图中目标A 的位置为(2,90°),则目标 B的位置是___________.
类型二 坐标系中点的坐标特征
6.点 P 在第四象限,且点 P 到x轴的距离是7,到y轴的距离是5,那么点 P 的坐标为 ( )
A.(-5,7) B.(-7,5) C.(7,-5) D.(5,-7)
7.在平面直角坐标系中,P(1,2),点 Q 在x 轴下方,PQ∥y轴,若PQ=5,则点 Q 的坐标为 ( )
A.(-4,2) B.(6,2) C.(1,-3) D.(1.7)
8.在平面直角坐标系中,点A(a,1)与点B(-2,b)关于原点对称,则a+b的值为 ( )
A.-3 B.-1 C.1 D.3
9.若点 P 位于第二象限,且到 x轴的距离为3个单位长度,到y轴的距离为2个单位长
度,则点 P 的坐标是 ( )
A.(-3,2) B.(-3,-2) C.(-2,3) D.(3,2)
10.在平面直角坐标系xOy中,点 P(5,-1)关于 y轴对称的点的坐标是__________.
11.已知点 A,B 的坐标分别为A(0,-3),B(0,5),点 C在x轴上,若△ABC的面积为20,则点C的坐标为___________.
12.已知点 分别根据下列条件求出点 P 的坐标.
(1)点 P在x轴上时,P点坐标为__________;
(2)点 P在 y轴上时,P点坐标为__________;
(3)点 P 到x轴,y轴的距离相等时,P 点坐标为__________;
(4)点P 的纵坐标比横坐标大3;
(5)点P 到x轴的距离为2,且在第三象限.
类型二 坐标系中图形的轴对称规律
13.剪纸艺术是最古老的中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点 E 的坐标为(m,1),其关于 y轴对称的点F 的坐标(2,n),则 的值为 ( )
A.1 B.-1 C. 32024 D.0
14.如图,正方形A A A A ,A A A A ,A A A A ,…(每个正方形从第三象限的顶点开始,按顺时针方向依次记为 A ,A ,A ,A ,A ,A ,A ,A ,A ,A ,A ,A ,…)的中心均在坐标原点 O,各边均与x轴或 y轴平行,若它们的边长依次是2,4,6,…,则顶点 的坐标为 ( )
15.△ABC在如图所示的网格中,点A 的坐标为(1,-1),点B 的坐标为(3,1).
(1)在网格中画出坐标系,并直接写出C 点坐标;
(2)作△ABC关于x轴对称的△A'B'C',并写出△A'B'C'三个顶点的坐标;
(3)若点 M 是在x 轴上的一个格点,且△ABM的面积为2,请直接写出点 M 的坐标.
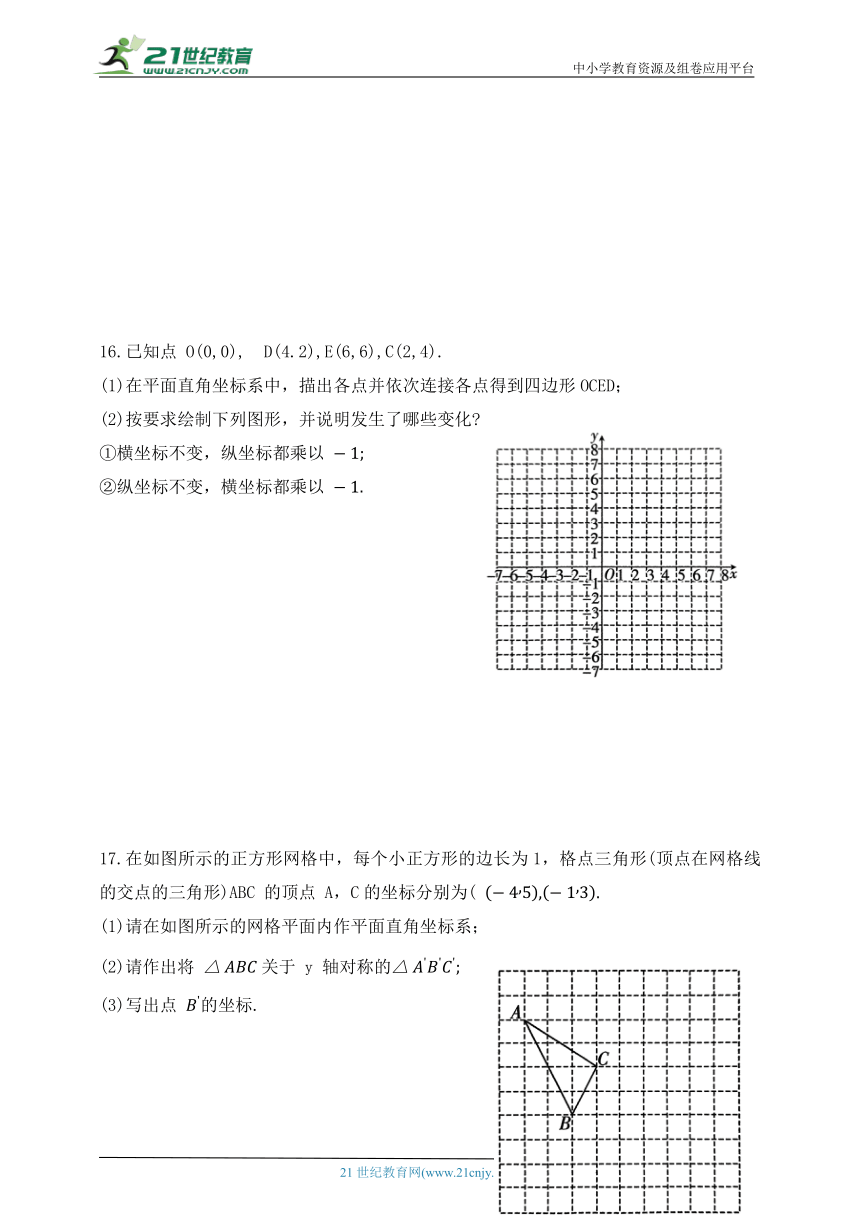
16.已知点 O(0,0), D(4.2),E(6,6),C(2,4).
(1)在平面直角坐标系中,描出各点并依次连接各点得到四边形OCED;
(2)按要求绘制下列图形,并说明发生了哪些变化
①横坐标不变,纵坐标都乘以
②纵坐标不变,横坐标都乘以
17.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点在网格线的交点的三角形)ABC 的顶点 A,C的坐标分别为(
(1)请在如图所示的网格平面内作平面直角坐标系;
(2)请作出将 关于 y 轴对称的
(3)写出点 的坐标.
18.已知点 点
(1)若点 A 在第二、四象限的角平分线上,求点 A 关于 y 轴的对称点A'的坐标.
(2)若线段 AB∥x轴,求线段AB的长度.
(3)若点 B到x轴的距离是到 y轴距离的2倍,求点 B 的坐标.
类型四 综合创新题
19.如图所示,在平面直角坐标系 xOy中,我们把横、纵坐标都是整数的点称为“整点”.已知点 A 的坐标为(5,0),点 B 在 x轴的上方,△OAB的面积为 则△OAB 内部(不含边界)的整点的个数最多为_________.
20.已知当m,n都是实数,且满足2m=6+n 时,称点 为“智慧点”.
(1)判断点 P(4, 10)是否为“智慧点”,并说明理由;
(2)若点 M(a,1-2a)是“智慧点”,请判断点 M 在第几象限 并说明理由.
参考答案
1. C 2. B 3. A 4. B 5.(5,30°) 6. D 7. C 8. C 9. C 10.(-5,-1)
11.(-5,0)或(5,0)
12.解:(1)因为点 P(a-2,2a+8)在x轴上, 所以2a+8=0,解得a=-4,
故a-2=-4-2=-6,则 P(-6,0);
故答案为:(-6,0);
(2)因为点 P(a-2,2a+8)在 y轴上,所以a-2=0,解得a=2,
故2a+8=2×2+8=12,则 P(0,12);
故答案为:(0,12);
(3)因为点 P 到x轴,y轴的距离相等,所以a-2=2a+8或a-2+2a+8=0,解得a=-10或a=-2,
故当a=-10时,a-2=-12,2a+8=-12,则 P(-12,-12);
故当a=-2时,a-2=-4,2a+8=4,则P(-4,4).
综上所述,P(-12,-12),(-4,4).故答案为:(-12,-12),(-4,4);
(4)因为点 P(a-2,2a+8)的纵坐标比横坐标大3,
所以2a+8-(a-2)=3,解得a=-7,
故a-2=-9,2a+8=2×(-7)+8=-6,则 P(-9,-6);
(5)因为点 P(a-2,2a+8)到x轴的距离为2,且在第三象限,
所以2a+8=-2,解得a=-5,故a-2=-5-2=-7,
则 P(-7,-2).
13. A 14. D
15.解:(1)如图1所示,C(3,4),
(2)如图 2 所示, 即为所求,
(3)设AB交x轴于点 D,如图3,
因为 所以 DM=2,
因为D(2,0),所以 M 的坐标为(0,0)或(4,0).
16.解:(1)四边形OCED 如图所示;
(2)①四边形( 如图所示,图形与四边形OCED 关于x轴对称;
②四边形( 如图所示,图形与四边形OCED关于y轴对称.
17.解:(1)(2)如图所示:
(3)点 的坐标为(2,1).
18.解:(1)因为点 A 在第二、四象限的角平分线上,所以
所以a=2,所以A(-3,3),所以点A 关于y轴的对称点. 的坐标为(3,3);
(2)因为线段AB∥x轴,所以2a-1=a-3,所以a=-2,
所以A(-3,-5),B(2,-5),所以线段AB=2-(-3)=2+3=5;
(3)因为点 B到x 轴的距离是到 y 轴距离的2倍,所以2|-a|=|a-3|,
所以a=1或a=-3,所以B(-1,-2)或B(3,-6).
19.6
20.解:(1)点 P 不是“智慧点”,由题意得 m-所以m=5,n=20,
所以2m=2×5=10,6+n=6+20=26,所以2m≠6+n,所以点 P(4, 10)不是“智慧点”;
(2)点 M 在第四象限,理由:因为点 M(a,1-2a)是“智慧点”,所以
所以m=a+1, n=2-4a,因为2m=6+n,所以2(a+1)=6+2-4a,解得a=1,
所以点 M (1,-1),所以点 M在第四象限.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 位置与坐标
章末复习
类型一 确定位置
1.下列数据中不能确定物体位置的是 ( )
A.电影票上的“5排8号” B.小明住在某小区3号楼7号
C.南偏西 D.东经 北纬 的城市
2.如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系以正东方向为x轴的正方向,以正北方向为 y轴的正方向,并且综合楼和教学楼的坐标分别是 和(1,2),则食堂的坐标是 ( )
A.(3,5) B.(-2,3) C.(2,4) D.(-1,2)
3.若点 在纵轴上,则点在 ( )
A.横轴上 B.纵轴上 C.坐标原点 D.第四象限内
4.如图是战机在空中展示的轴对称队形.以飞机 B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机 E 的坐标为(40,a),则飞机 D 的坐标为 ( )
5.如图所示为一台雷达探测相关目标得到的结果,若记图中目标A 的位置为(2,90°),则目标 B的位置是___________.
类型二 坐标系中点的坐标特征
6.点 P 在第四象限,且点 P 到x轴的距离是7,到y轴的距离是5,那么点 P 的坐标为 ( )
A.(-5,7) B.(-7,5) C.(7,-5) D.(5,-7)
7.在平面直角坐标系中,P(1,2),点 Q 在x 轴下方,PQ∥y轴,若PQ=5,则点 Q 的坐标为 ( )
A.(-4,2) B.(6,2) C.(1,-3) D.(1.7)
8.在平面直角坐标系中,点A(a,1)与点B(-2,b)关于原点对称,则a+b的值为 ( )
A.-3 B.-1 C.1 D.3
9.若点 P 位于第二象限,且到 x轴的距离为3个单位长度,到y轴的距离为2个单位长
度,则点 P 的坐标是 ( )
A.(-3,2) B.(-3,-2) C.(-2,3) D.(3,2)
10.在平面直角坐标系xOy中,点 P(5,-1)关于 y轴对称的点的坐标是__________.
11.已知点 A,B 的坐标分别为A(0,-3),B(0,5),点 C在x轴上,若△ABC的面积为20,则点C的坐标为___________.
12.已知点 分别根据下列条件求出点 P 的坐标.
(1)点 P在x轴上时,P点坐标为__________;
(2)点 P在 y轴上时,P点坐标为__________;
(3)点 P 到x轴,y轴的距离相等时,P 点坐标为__________;
(4)点P 的纵坐标比横坐标大3;
(5)点P 到x轴的距离为2,且在第三象限.
类型二 坐标系中图形的轴对称规律
13.剪纸艺术是最古老的中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点 E 的坐标为(m,1),其关于 y轴对称的点F 的坐标(2,n),则 的值为 ( )
A.1 B.-1 C. 32024 D.0
14.如图,正方形A A A A ,A A A A ,A A A A ,…(每个正方形从第三象限的顶点开始,按顺时针方向依次记为 A ,A ,A ,A ,A ,A ,A ,A ,A ,A ,A ,A ,…)的中心均在坐标原点 O,各边均与x轴或 y轴平行,若它们的边长依次是2,4,6,…,则顶点 的坐标为 ( )
15.△ABC在如图所示的网格中,点A 的坐标为(1,-1),点B 的坐标为(3,1).
(1)在网格中画出坐标系,并直接写出C 点坐标;
(2)作△ABC关于x轴对称的△A'B'C',并写出△A'B'C'三个顶点的坐标;
(3)若点 M 是在x 轴上的一个格点,且△ABM的面积为2,请直接写出点 M 的坐标.
16.已知点 O(0,0), D(4.2),E(6,6),C(2,4).
(1)在平面直角坐标系中,描出各点并依次连接各点得到四边形OCED;
(2)按要求绘制下列图形,并说明发生了哪些变化
①横坐标不变,纵坐标都乘以
②纵坐标不变,横坐标都乘以
17.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点在网格线的交点的三角形)ABC 的顶点 A,C的坐标分别为(
(1)请在如图所示的网格平面内作平面直角坐标系;
(2)请作出将 关于 y 轴对称的
(3)写出点 的坐标.
18.已知点 点
(1)若点 A 在第二、四象限的角平分线上,求点 A 关于 y 轴的对称点A'的坐标.
(2)若线段 AB∥x轴,求线段AB的长度.
(3)若点 B到x轴的距离是到 y轴距离的2倍,求点 B 的坐标.
类型四 综合创新题
19.如图所示,在平面直角坐标系 xOy中,我们把横、纵坐标都是整数的点称为“整点”.已知点 A 的坐标为(5,0),点 B 在 x轴的上方,△OAB的面积为 则△OAB 内部(不含边界)的整点的个数最多为_________.
20.已知当m,n都是实数,且满足2m=6+n 时,称点 为“智慧点”.
(1)判断点 P(4, 10)是否为“智慧点”,并说明理由;
(2)若点 M(a,1-2a)是“智慧点”,请判断点 M 在第几象限 并说明理由.
参考答案
1. C 2. B 3. A 4. B 5.(5,30°) 6. D 7. C 8. C 9. C 10.(-5,-1)
11.(-5,0)或(5,0)
12.解:(1)因为点 P(a-2,2a+8)在x轴上, 所以2a+8=0,解得a=-4,
故a-2=-4-2=-6,则 P(-6,0);
故答案为:(-6,0);
(2)因为点 P(a-2,2a+8)在 y轴上,所以a-2=0,解得a=2,
故2a+8=2×2+8=12,则 P(0,12);
故答案为:(0,12);
(3)因为点 P 到x轴,y轴的距离相等,所以a-2=2a+8或a-2+2a+8=0,解得a=-10或a=-2,
故当a=-10时,a-2=-12,2a+8=-12,则 P(-12,-12);
故当a=-2时,a-2=-4,2a+8=4,则P(-4,4).
综上所述,P(-12,-12),(-4,4).故答案为:(-12,-12),(-4,4);
(4)因为点 P(a-2,2a+8)的纵坐标比横坐标大3,
所以2a+8-(a-2)=3,解得a=-7,
故a-2=-9,2a+8=2×(-7)+8=-6,则 P(-9,-6);
(5)因为点 P(a-2,2a+8)到x轴的距离为2,且在第三象限,
所以2a+8=-2,解得a=-5,故a-2=-5-2=-7,
则 P(-7,-2).
13. A 14. D
15.解:(1)如图1所示,C(3,4),
(2)如图 2 所示, 即为所求,
(3)设AB交x轴于点 D,如图3,
因为 所以 DM=2,
因为D(2,0),所以 M 的坐标为(0,0)或(4,0).
16.解:(1)四边形OCED 如图所示;
(2)①四边形( 如图所示,图形与四边形OCED 关于x轴对称;
②四边形( 如图所示,图形与四边形OCED关于y轴对称.
17.解:(1)(2)如图所示:
(3)点 的坐标为(2,1).
18.解:(1)因为点 A 在第二、四象限的角平分线上,所以
所以a=2,所以A(-3,3),所以点A 关于y轴的对称点. 的坐标为(3,3);
(2)因为线段AB∥x轴,所以2a-1=a-3,所以a=-2,
所以A(-3,-5),B(2,-5),所以线段AB=2-(-3)=2+3=5;
(3)因为点 B到x 轴的距离是到 y 轴距离的2倍,所以2|-a|=|a-3|,
所以a=1或a=-3,所以B(-1,-2)或B(3,-6).
19.6
20.解:(1)点 P 不是“智慧点”,由题意得 m-所以m=5,n=20,
所以2m=2×5=10,6+n=6+20=26,所以2m≠6+n,所以点 P(4, 10)不是“智慧点”;
(2)点 M 在第四象限,理由:因为点 M(a,1-2a)是“智慧点”,所以
所以m=a+1, n=2-4a,因为2m=6+n,所以2(a+1)=6+2-4a,解得a=1,
所以点 M (1,-1),所以点 M在第四象限.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
