第十一章 三角形(B卷)寒假练习(含详解)2024-2025学年人教版八年级数学
文档属性
| 名称 | 第十一章 三角形(B卷)寒假练习(含详解)2024-2025学年人教版八年级数学 |  | |
| 格式 | docx | ||
| 文件大小 | 425.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-25 23:00:01 | ||
图片预览


文档简介
三角形(B卷)
一、选择题。
1.下列各组图形中,BD是的高的图形是( )
A. B. C. D.
2.若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )
A.1 B.2 C.4 D.8
3.如图,在中,,,BD平分,则的度数是( )
A.30° B.35° C.40° D.70°
4.一个多边形的内角和比外角和的三倍少180°,则这个多边形是( )
A.四边形 B.六边形 C.五边形 D.七边形
5.如图,在中,,分别是边上的中线和高,点D在点E的左侧,已知,,,( )
A.1cm B.2cm C.3cm D.4cm
6.如图,在中,若,,是的两条中线,则的周长是( )
A.22 B.26 C.35 D.45
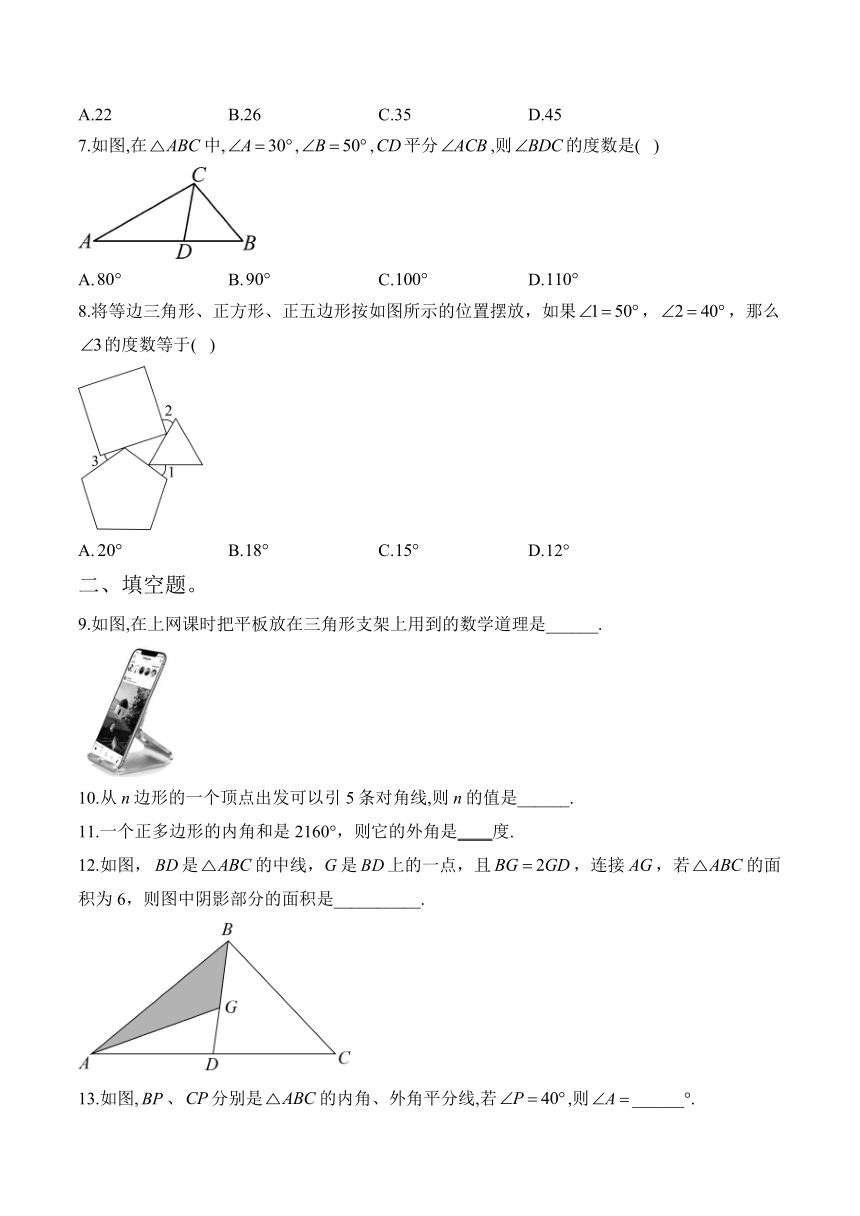
7.如图,在中,,,平分,则的度数是( )
A. B. C. D.
8.将等边三角形、正方形、正五边形按如图所示的位置摆放,如果,,那么的度数等于( )
A. B. C. D.
二、填空题。
9.如图,在上网课时把平板放在三角形支架上用到的数学道理是______.
10.从n边形的一个顶点出发可以引5条对角线,则n的值是______.
11.一个正多边形的内角和是2160°,则它的外角是____度.
12.如图,是的中线,G是上的一点,且,连接,若的面积为6,则图中阴影部分的面积是__________.
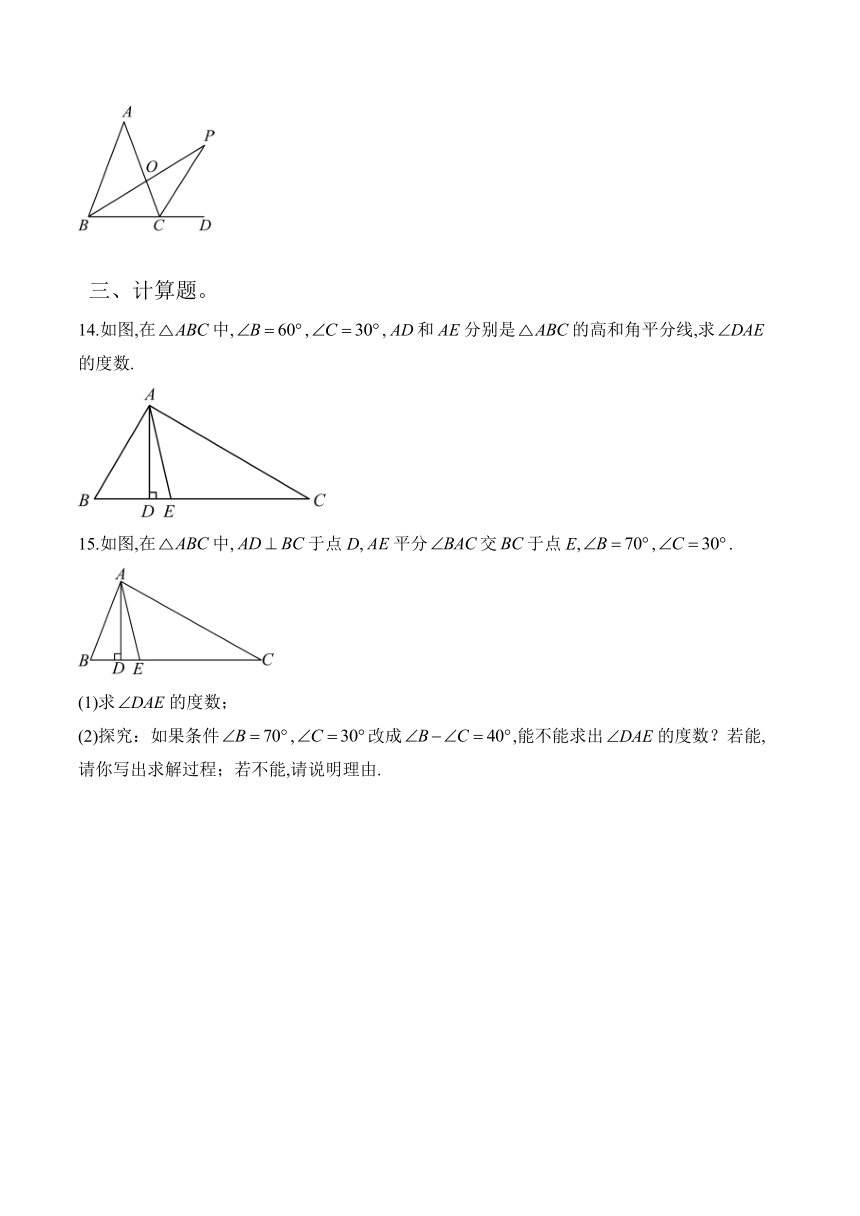
13.如图,、分别是的内角、外角平分线,若,则______°.
三、计算题。
14.如图,在中,,,和分别是的高和角平分线,求的度数.
15.如图,在中,于点D,平分交于点E,,.
(1)求的度数;
(2)探究:如果条件,改成,能不能求出的度数?若能,请你写出求解过程;若不能,请说明理由.
答案以及解析
1.答案:B
解析:根据三角形高的定义可知,只有选项B中的线段BD是的高.
故选B.
2.答案:C
解析:根据三角形的三边关系得,即,则选项中4符合题意,
故选:C.
3.答案:B
解析:∵,,
∴,
∵BD平分,
∴,
故选:B.
4.答案:D
解析:设所求n边形边数为n,
则,
解得,
故选:D.
5.答案:C
解析:AD,AE分别是边BC上的中线和高,,,
,
,
解得:(cm),
,
(cm).
故选:C.
6.答案:B
解析:∵,
∴,
∵,
∵是的两条中线,
∴,,
∴的周长是,
故选:B.
7.答案:A
解析:∵在中,,,
∴
,
∵平分,
∴,
∴.
故选:A.
8.答案:D
解析:等边三角形的每个内角为,
正方形的每个内角为,
正五边形的每个内角为,
如图,
的外角和等于,
,
即,
,
,,
,
故选:D.
9.答案:三角形具有稳定性
解析:在上网课时把平板放在三角形支架上用到的数学道理是三角形具有稳定性,
故答案为:三角形具有稳定性.
10.答案:8
解析:设多边形有n条边,
则,
解得.
11.答案:
解析:设这个多边形的边数为n,
,
解得:,
则该正多边形的每个外角为,
故答案为:.
12.答案:2
解析:∵是的中线,的面积为6,
∴,
∵,
∴,
∴,
即图中阴影部分的面积是2.
故答案为:2
13.答案:80
解析:∵、分别是的内角、外角平分线,
∴,
∵
∴
∴
∴
∴.
故答案为:80.
14.答案:∠DAE=15°.
解析:在中,,
∴
∵是的角平分线
∴,
∵是的高,
∴
∴在中,
∴.
15.答案:(1)
(2)能,求解见解析
解析:(1)∵,
∴,
∵平分,
∴;
∵,
∴,
∵,
∴,
∴;
(2)能,解答如下:
∵,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
一、选择题。
1.下列各组图形中,BD是的高的图形是( )
A. B. C. D.
2.若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )
A.1 B.2 C.4 D.8
3.如图,在中,,,BD平分,则的度数是( )
A.30° B.35° C.40° D.70°
4.一个多边形的内角和比外角和的三倍少180°,则这个多边形是( )
A.四边形 B.六边形 C.五边形 D.七边形
5.如图,在中,,分别是边上的中线和高,点D在点E的左侧,已知,,,( )
A.1cm B.2cm C.3cm D.4cm
6.如图,在中,若,,是的两条中线,则的周长是( )
A.22 B.26 C.35 D.45
7.如图,在中,,,平分,则的度数是( )
A. B. C. D.
8.将等边三角形、正方形、正五边形按如图所示的位置摆放,如果,,那么的度数等于( )
A. B. C. D.
二、填空题。
9.如图,在上网课时把平板放在三角形支架上用到的数学道理是______.
10.从n边形的一个顶点出发可以引5条对角线,则n的值是______.
11.一个正多边形的内角和是2160°,则它的外角是____度.
12.如图,是的中线,G是上的一点,且,连接,若的面积为6,则图中阴影部分的面积是__________.
13.如图,、分别是的内角、外角平分线,若,则______°.
三、计算题。
14.如图,在中,,,和分别是的高和角平分线,求的度数.
15.如图,在中,于点D,平分交于点E,,.
(1)求的度数;
(2)探究:如果条件,改成,能不能求出的度数?若能,请你写出求解过程;若不能,请说明理由.
答案以及解析
1.答案:B
解析:根据三角形高的定义可知,只有选项B中的线段BD是的高.
故选B.
2.答案:C
解析:根据三角形的三边关系得,即,则选项中4符合题意,
故选:C.
3.答案:B
解析:∵,,
∴,
∵BD平分,
∴,
故选:B.
4.答案:D
解析:设所求n边形边数为n,
则,
解得,
故选:D.
5.答案:C
解析:AD,AE分别是边BC上的中线和高,,,
,
,
解得:(cm),
,
(cm).
故选:C.
6.答案:B
解析:∵,
∴,
∵,
∵是的两条中线,
∴,,
∴的周长是,
故选:B.
7.答案:A
解析:∵在中,,,
∴
,
∵平分,
∴,
∴.
故选:A.
8.答案:D
解析:等边三角形的每个内角为,
正方形的每个内角为,
正五边形的每个内角为,
如图,
的外角和等于,
,
即,
,
,,
,
故选:D.
9.答案:三角形具有稳定性
解析:在上网课时把平板放在三角形支架上用到的数学道理是三角形具有稳定性,
故答案为:三角形具有稳定性.
10.答案:8
解析:设多边形有n条边,
则,
解得.
11.答案:
解析:设这个多边形的边数为n,
,
解得:,
则该正多边形的每个外角为,
故答案为:.
12.答案:2
解析:∵是的中线,的面积为6,
∴,
∵,
∴,
∴,
即图中阴影部分的面积是2.
故答案为:2
13.答案:80
解析:∵、分别是的内角、外角平分线,
∴,
∵
∴
∴
∴
∴.
故答案为:80.
14.答案:∠DAE=15°.
解析:在中,,
∴
∵是的角平分线
∴,
∵是的高,
∴
∴在中,
∴.
15.答案:(1)
(2)能,求解见解析
解析:(1)∵,
∴,
∵平分,
∴;
∵,
∴,
∵,
∴,
∴;
(2)能,解答如下:
∵,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
同课章节目录
