【2025春新教材】人教版七年级下册数学7.2.2平行线的判定 课件(共35张PPT)
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学7.2.2平行线的判定 课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 19:31:13 | ||
图片预览



文档简介
(共35张PPT)
7.2.2 平行线的判定
第7章 相交线与平行线
人教版(新教材)数学七年级下册
1.掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行.
2.经历平行线判定方法的探究过程,从中体会转化的数学思想.
3.能够根据平行线的判定方法进行简单的推理,感受数学语言的简洁美,并能将学到的知识应用到生活中去,提高应用意识.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
情境引入
问题1 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
平行线的定义→对边所在的直线永不相交
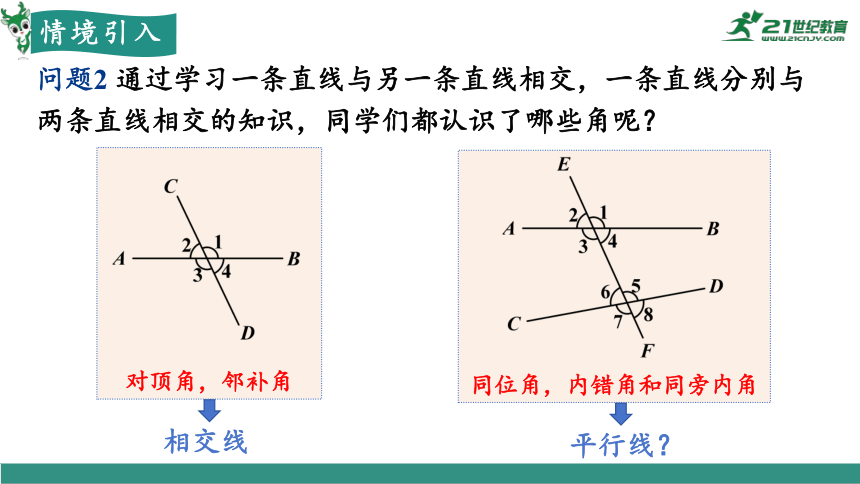
同位角,内错角和同旁内角
对顶角,邻补角
情境引入
问题2 通过学习一条直线与另一条直线相交,一条直线分别与两条直线相交的知识,同学们都认识了哪些角呢?
相交线
平行线?
合作探究
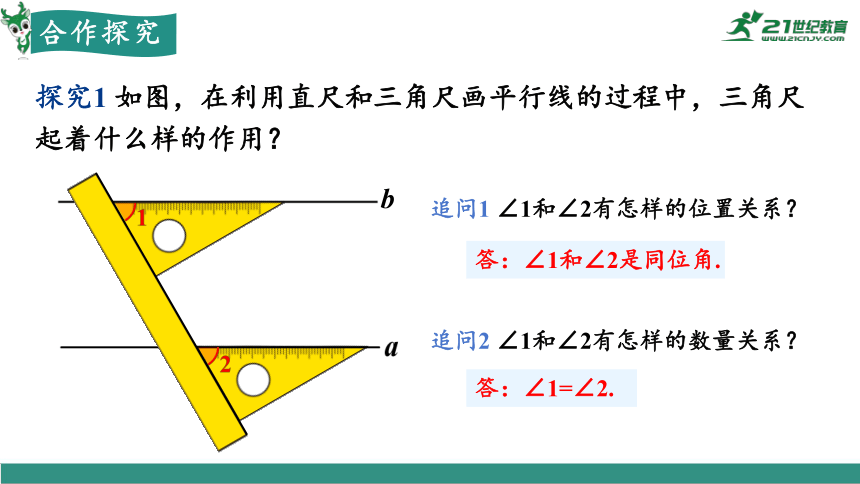
探究1 如图,在利用直尺和三角尺画平行线的过程中,三角尺起着什么样的作用?
b
追问1 ∠1和∠2有怎样的位置关系?
追问2 ∠1和∠2有怎样的数量关系?
答:∠1=∠2.
答:∠1和∠2是同位角.
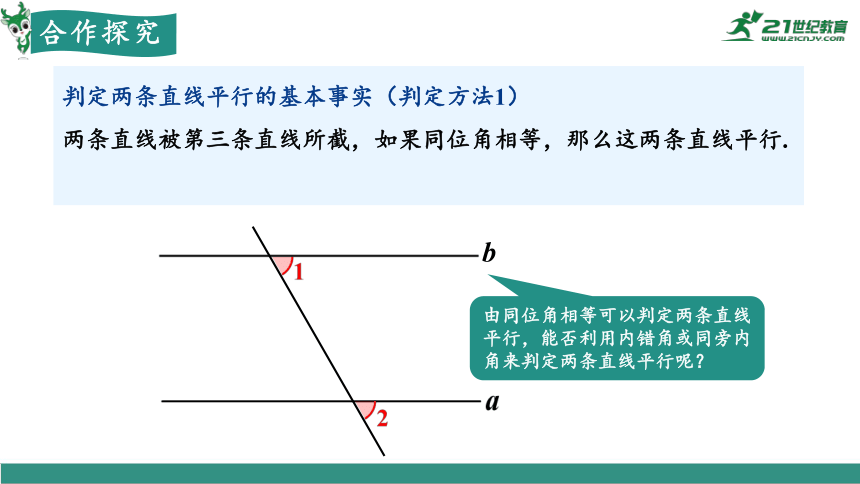
判定两条直线平行的基本事实(判定方法1)
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.(因为 ∠1=∠2,所以 a∥b.)
b
由同位角相等可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
合作探究
探究2 如图,直线a,b被直线c所截.
(1)内错角∠1与∠2满足什么条件时,能得出a∥b?
解:当∠1=∠2时,能得出a∥b.
理由如下:
因为∠1=∠2(已知),
∠2=∠4(对顶角相等),
所以∠1=∠4(等量代换),
所以a∥b(同位角相等,两直线平行).
合作探究
合作探究
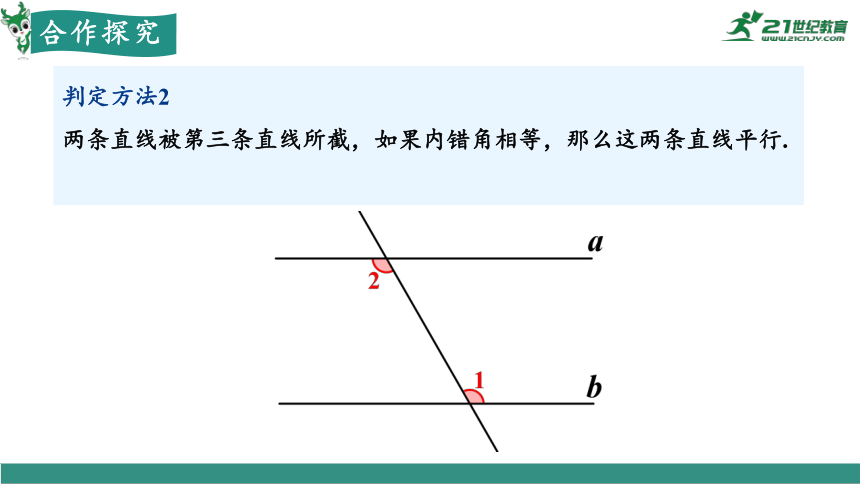
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.(因为 ∠1=∠2,所以 a∥b.)
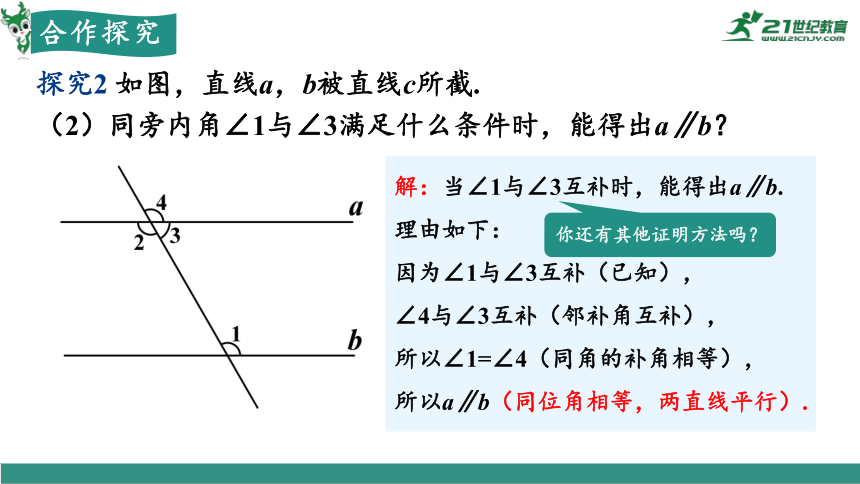
探究2 如图,直线a,b被直线c所截.
(2)同旁内角∠1与∠3满足什么条件时,能得出a∥b?
解:当∠1与∠3互补时,能得出a∥b.
理由如下:
因为∠1与∠3互补(已知),
∠4与∠3互补(邻补角互补),
所以∠1=∠4(同角的补角相等),
所以a∥b(同位角相等,两直线平行).
你还有其他证明方法吗?
合作探究
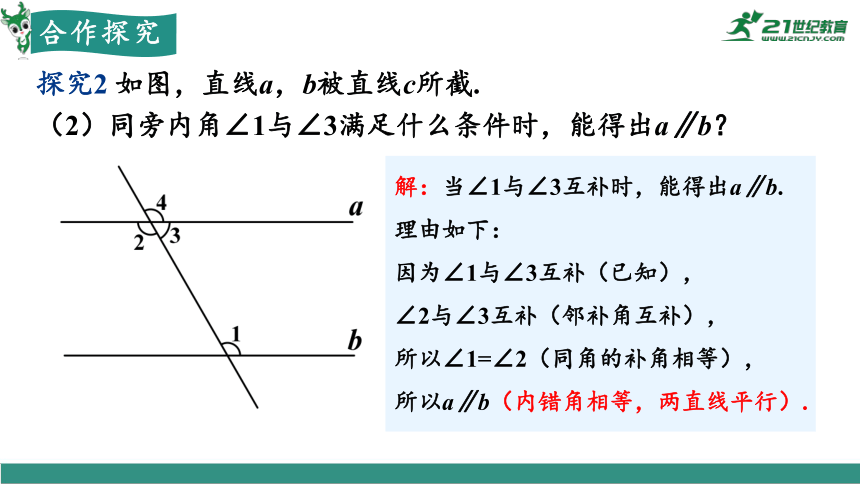
探究2 如图,直线a,b被直线c所截.
(2)同旁内角∠1与∠3满足什么条件时,能得出a∥b?
解:当∠1与∠3互补时,能得出a∥b.
理由如下:
因为∠1与∠3互补(已知),
∠2与∠3互补(邻补角互补),
所以∠1=∠2(同角的补角相等),
所以a∥b(内错角相等,两直线平行).
合作探究
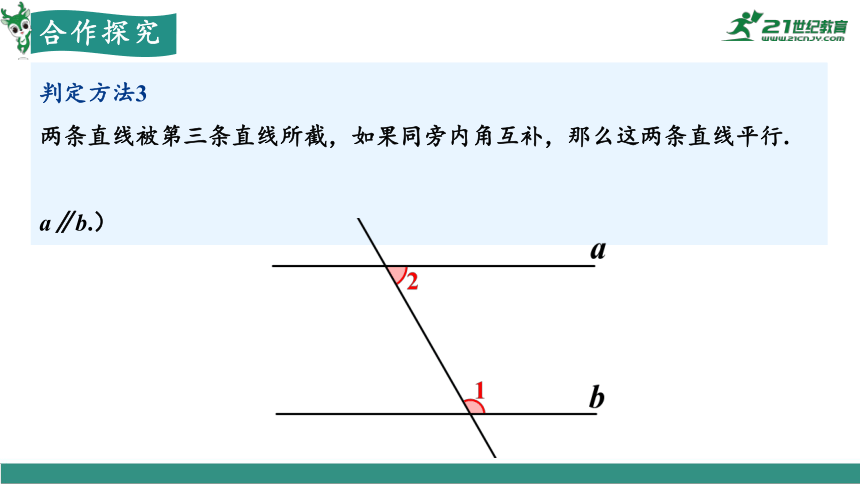
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.(因为 ∠1+∠2=180°,所以 a∥b.)
合作探究
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.
判定方法1
同位角相等,两直线平行.
判定方法2
内错角相等,两直线平行.
判定方法3
同旁内角互补,两直线平行.
转化
转化
转化
证明
证明
证明
合作探究
问题解决 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
合作探究
度量∠1和∠2的度数,若∠1=∠2,则上下两条对边平行.(方法不唯一)
如图,直线a,b,c是平面内的三条直
线,如果b⊥a,c⊥a,那么b∥c吗?
典例分析
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
转化1 自然语言→符号语言
解:这两条直线平行.理由如下:
∵b⊥a,
∴∠1=90°,
同理 ∠2=90°,
∴∠1=∠2.
又 ∠1和∠2是同位角,
∴b∥c(同位角相等,两直线平行).
1
2
转化2 平行线→同位角→垂直
如图,直线a,b,c是平面内的三条直线,如果b⊥a,c⊥a,那么b∥c吗?
符号“∵”表示“因为”,
符号“∴”表示“所以”.
典例分析
解:这两条直线平行.理由如下:
∵b⊥a,
∴∠1=90°,
同理 ∠2=90°,
∴∠1=∠2.
又 ∠1和∠2是内错角,
∴b∥c(内错角相等,两直线平行).
1
2
转化2 平行线→内错角→垂直
如图,直线a,b,c是平面内的三条直线,如果b⊥a,c⊥a,那么b∥c吗?
你还有其他转化方法吗?
典例分析
解:这两条直线平行.理由如下:
∵b⊥a,
∴∠1=90°,
同理 ∠2=90°,
∴∠1与∠2互补.
又 ∠1与∠2是同旁内角,
∴b∥c(同旁内角互补,两直线平行).
1
2
转化2 平行线→同旁内角→垂直
如图,直线a,b,c是平面内的三条直线,如果b⊥a,c⊥a,那么b∥c吗?
典例分析
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
在同一平面内,垂直于同一条直线的两条直线互相平行.
转化3 符号语言→自然语言
这句话可以省略吗?为什么?
典例分析
巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(1)如果∠B=∠DCG,那么可以判断哪两条直线平行?为什么?
巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(2)如果∠D=∠DCG, 那么可以判断哪两条直线平行?为什么?
巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(3)如果∠D+∠DFE=180°,那么可以判断哪两条直线平行?为什么?
2. 如图,木工常用角尺画平行线,你能说出其中的道理吗?
巩固练习
同位角相等,两直线平行.
3. 如图,在下列条件中,能判断直线a∥b的是( )
A.∠2+∠5=180°
B.∠2=∠4
C.∠4+∠5=180°
D.∠1=∠3
巩固练习
D
4. 在铺设钢轨时,两条钢轨必须是互相平行的.如图,已知∠2是直角,要判断两条钢轨是否平行,只需要再度量图中标出的哪个角,为什么?
钢轨
巩固练习
同旁内角互补,两直线平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
5. 如左图是两条道路互相垂直的交叉路口,你能画出它的平面示意图(用两条平行线段表示一条道路)吗?你能用类似的方法,画出右图的平面示意图吗?你能画出两条道路成45°角的交叉路口的平面示意图吗?
巩固练习
归纳总结
平行线的判定 判定方法 简单说成
1. 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 同位角相等,
两直线平行.
2. 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 内错角相等,
两直线平行.
3. 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 同旁内角互补,
两直线平行.
感受中考
1. (2024 郴州)如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠1=∠2
D
感受中考
2. (2024 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90°
B.∠3=90°
C.∠4=90°
D.∠5=90°
C
感受中考
3. (2024 兰州)将一副三角板如图摆放,则 ∥ ,理由是 .
BC
ED
内错角相等,两直线平行
感受中考
4. (2024 咸宁)如图,请填写一个条件,使结论成立:
∵ ,∴a∥b.
∠1=∠4
方法2:∠2=∠4
方法3:∠3+∠4=180°
同位角相等,两直线平行
关于平行线的基本事实
小结梳理
平行线的判定
平行线的概念
推论
平行线
内错角相等,两直线平行
同旁内角互补,两直线平行
布置作业
必做题:习题7.2 第2题,第12题.
1
探究性作业:(2024 苏州)
如图,在正方形网格内,线段PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是( )
A.连接AB,则AB∥PQ
B.连接BC,则BC∥PQ
C.连接BD,则BD⊥PQ
D.连接AD,则AD⊥PQ
2
谢谢观看
7.2.2 平行线的判定
第7章 相交线与平行线
人教版(新教材)数学七年级下册
1.掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行.
2.经历平行线判定方法的探究过程,从中体会转化的数学思想.
3.能够根据平行线的判定方法进行简单的推理,感受数学语言的简洁美,并能将学到的知识应用到生活中去,提高应用意识.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
情境引入
问题1 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
平行线的定义→对边所在的直线永不相交
同位角,内错角和同旁内角
对顶角,邻补角
情境引入
问题2 通过学习一条直线与另一条直线相交,一条直线分别与两条直线相交的知识,同学们都认识了哪些角呢?
相交线
平行线?
合作探究
探究1 如图,在利用直尺和三角尺画平行线的过程中,三角尺起着什么样的作用?
b
追问1 ∠1和∠2有怎样的位置关系?
追问2 ∠1和∠2有怎样的数量关系?
答:∠1=∠2.
答:∠1和∠2是同位角.
判定两条直线平行的基本事实(判定方法1)
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.(因为 ∠1=∠2,所以 a∥b.)
b
由同位角相等可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
合作探究
探究2 如图,直线a,b被直线c所截.
(1)内错角∠1与∠2满足什么条件时,能得出a∥b?
解:当∠1=∠2时,能得出a∥b.
理由如下:
因为∠1=∠2(已知),
∠2=∠4(对顶角相等),
所以∠1=∠4(等量代换),
所以a∥b(同位角相等,两直线平行).
合作探究
合作探究
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.(因为 ∠1=∠2,所以 a∥b.)
探究2 如图,直线a,b被直线c所截.
(2)同旁内角∠1与∠3满足什么条件时,能得出a∥b?
解:当∠1与∠3互补时,能得出a∥b.
理由如下:
因为∠1与∠3互补(已知),
∠4与∠3互补(邻补角互补),
所以∠1=∠4(同角的补角相等),
所以a∥b(同位角相等,两直线平行).
你还有其他证明方法吗?
合作探究
探究2 如图,直线a,b被直线c所截.
(2)同旁内角∠1与∠3满足什么条件时,能得出a∥b?
解:当∠1与∠3互补时,能得出a∥b.
理由如下:
因为∠1与∠3互补(已知),
∠2与∠3互补(邻补角互补),
所以∠1=∠2(同角的补角相等),
所以a∥b(内错角相等,两直线平行).
合作探究
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.(因为 ∠1+∠2=180°,所以 a∥b.)
合作探究
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.
判定方法1
同位角相等,两直线平行.
判定方法2
内错角相等,两直线平行.
判定方法3
同旁内角互补,两直线平行.
转化
转化
转化
证明
证明
证明
合作探究
问题解决 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
合作探究
度量∠1和∠2的度数,若∠1=∠2,则上下两条对边平行.(方法不唯一)
如图,直线a,b,c是平面内的三条直
线,如果b⊥a,c⊥a,那么b∥c吗?
典例分析
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
转化1 自然语言→符号语言
解:这两条直线平行.理由如下:
∵b⊥a,
∴∠1=90°,
同理 ∠2=90°,
∴∠1=∠2.
又 ∠1和∠2是同位角,
∴b∥c(同位角相等,两直线平行).
1
2
转化2 平行线→同位角→垂直
如图,直线a,b,c是平面内的三条直线,如果b⊥a,c⊥a,那么b∥c吗?
符号“∵”表示“因为”,
符号“∴”表示“所以”.
典例分析
解:这两条直线平行.理由如下:
∵b⊥a,
∴∠1=90°,
同理 ∠2=90°,
∴∠1=∠2.
又 ∠1和∠2是内错角,
∴b∥c(内错角相等,两直线平行).
1
2
转化2 平行线→内错角→垂直
如图,直线a,b,c是平面内的三条直线,如果b⊥a,c⊥a,那么b∥c吗?
你还有其他转化方法吗?
典例分析
解:这两条直线平行.理由如下:
∵b⊥a,
∴∠1=90°,
同理 ∠2=90°,
∴∠1与∠2互补.
又 ∠1与∠2是同旁内角,
∴b∥c(同旁内角互补,两直线平行).
1
2
转化2 平行线→同旁内角→垂直
如图,直线a,b,c是平面内的三条直线,如果b⊥a,c⊥a,那么b∥c吗?
典例分析
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
在同一平面内,垂直于同一条直线的两条直线互相平行.
转化3 符号语言→自然语言
这句话可以省略吗?为什么?
典例分析
巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(1)如果∠B=∠DCG,那么可以判断哪两条直线平行?为什么?
巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(2)如果∠D=∠DCG, 那么可以判断哪两条直线平行?为什么?
巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(3)如果∠D+∠DFE=180°,那么可以判断哪两条直线平行?为什么?
2. 如图,木工常用角尺画平行线,你能说出其中的道理吗?
巩固练习
同位角相等,两直线平行.
3. 如图,在下列条件中,能判断直线a∥b的是( )
A.∠2+∠5=180°
B.∠2=∠4
C.∠4+∠5=180°
D.∠1=∠3
巩固练习
D
4. 在铺设钢轨时,两条钢轨必须是互相平行的.如图,已知∠2是直角,要判断两条钢轨是否平行,只需要再度量图中标出的哪个角,为什么?
钢轨
巩固练习
同旁内角互补,两直线平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
5. 如左图是两条道路互相垂直的交叉路口,你能画出它的平面示意图(用两条平行线段表示一条道路)吗?你能用类似的方法,画出右图的平面示意图吗?你能画出两条道路成45°角的交叉路口的平面示意图吗?
巩固练习
归纳总结
平行线的判定 判定方法 简单说成
1. 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 同位角相等,
两直线平行.
2. 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 内错角相等,
两直线平行.
3. 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 同旁内角互补,
两直线平行.
感受中考
1. (2024 郴州)如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠1=∠2
D
感受中考
2. (2024 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90°
B.∠3=90°
C.∠4=90°
D.∠5=90°
C
感受中考
3. (2024 兰州)将一副三角板如图摆放,则 ∥ ,理由是 .
BC
ED
内错角相等,两直线平行
感受中考
4. (2024 咸宁)如图,请填写一个条件,使结论成立:
∵ ,∴a∥b.
∠1=∠4
方法2:∠2=∠4
方法3:∠3+∠4=180°
同位角相等,两直线平行
关于平行线的基本事实
小结梳理
平行线的判定
平行线的概念
推论
平行线
内错角相等,两直线平行
同旁内角互补,两直线平行
布置作业
必做题:习题7.2 第2题,第12题.
1
探究性作业:(2024 苏州)
如图,在正方形网格内,线段PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是( )
A.连接AB,则AB∥PQ
B.连接BC,则BC∥PQ
C.连接BD,则BD⊥PQ
D.连接AD,则AD⊥PQ
2
谢谢观看
同课章节目录
