【2025春新教材】人教版七年级下册数学8.1平方根(第1课时平方根)课件(共35张PPT)
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学8.1平方根(第1课时平方根)课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览








文档简介
(共35张PPT)
8.1 平方根
第1课时 平方根
第8章 实数
人教版(新教材)数学七年级下册
1.正确理解平方根的概念,会求一个数的平方根
2. 会表示一个数的平方根.
3.学生经历由特殊到一般,培养学生观察,归纳,类比的能力.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
复习引入
运算 加 减 乘 除 乘方
符号表示 + -
运算结果 和 差 积 商 幂
运算关系
完成表格信息
互为逆运算
互为逆运算
?
复习引入
+1
-1
+0.4
-0.4
0.16
1
-
+
①任何数的平方都是一个非负数
0
0
②互为相反数的两个数的平方相等
新课讲解
0
1
0.16
+1
-1
+0.4
-0.4
-
+
0
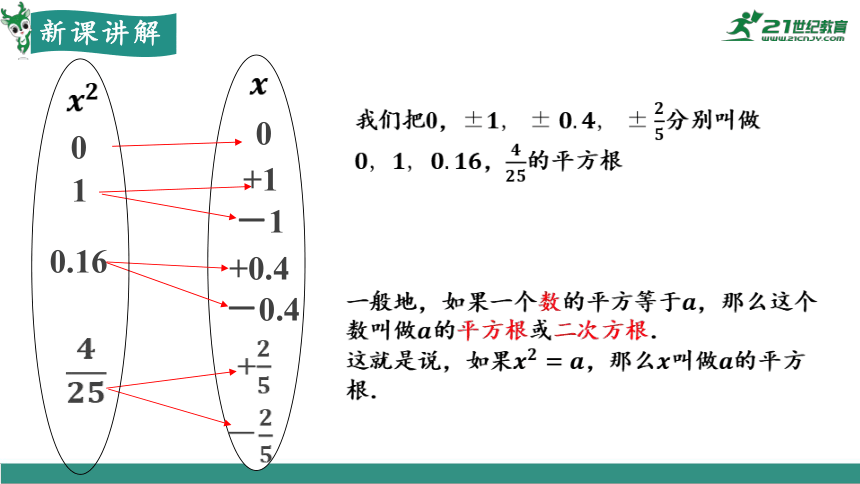
我们把0,分别叫做,的平方根
一般地,如果一个数的平方等于,那么这个数叫做的平方根或二次方根.
这就是说,如果,那么叫做的平方根.
新课讲解
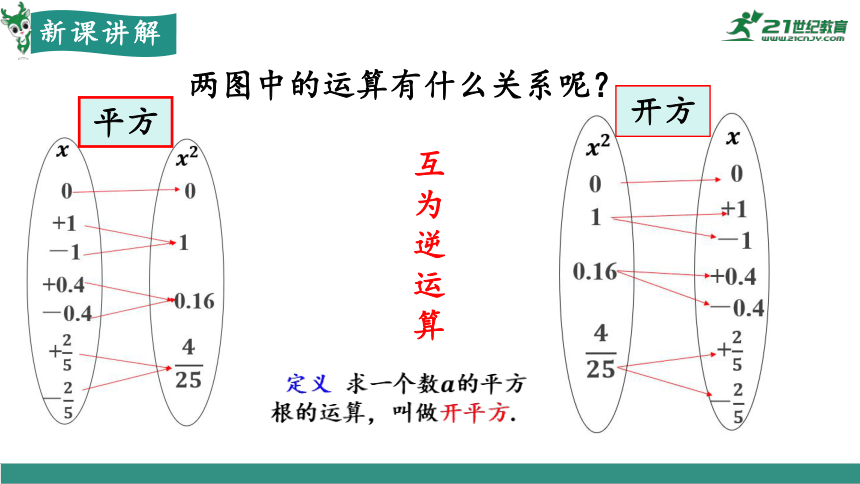
互为逆运算
定义 求一个数的平方根的运算,叫做开平方.
两图中的运算有什么关系呢?
开方
平方
新课讲解
1.判断下列说法是否正确。
①是的平方根. ( )
②是的平方根. ( )
③是的平方根. ( )
④的平方根是. ( )
⑤是的一个平方根. ( )
⑥-的平方根是; ( )
⑦一个数的一个平方根是,另一个平方根一定是 ( )
×
√
√
√
×
×
√
典例讲解
例1 求下列各数的平方根:
(1) (2) (3) (4)
解(1)∵,∴的平方根是
(2)∵,∴的平方根是
(3)∵,∴的平方根是
(4)∵,∴的平方根是
注意:求一个数的平方根可将带分数化为假分数!
典例讲解
例1 求下列各数的平方根:
(5) (6) (7) (8)
解(5)∵,∴的平方根是
(6)∵,∴的平方根是
(7)∵任何数的平方都是非负数,∴没有平方根
(8)∵,∴的平方根是
典例讲解
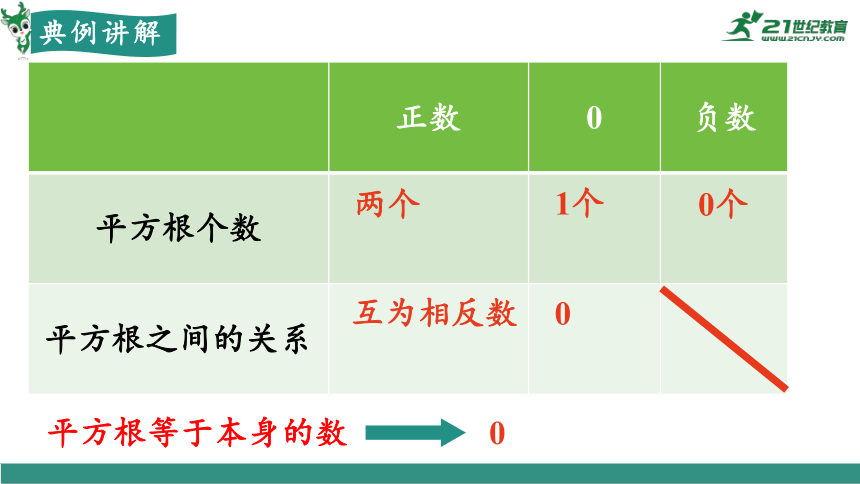
正数 0 负数
平方根个数
平方根之间的关系
两个
1个
0个
互为相反数
0
平方根等于本身的数
0
典例讲解
例2.求下列各式中的值
(1) (2)
解(1)原式可变形为:
∵
∴或
解(2)原式可变形为:
∵
∴或
开方
解方程
变形
典例讲解
例2.解下列方程
(3) (4)
解(4)∵
∴或
解得或
解(3)原式可变形为:
∵
∴或
解得:或
思路点拨:
的值
新知讲解
的平方根表示为
=
表示的正的平方根
表示的负的平方根
读作:正负根号
表示的平方根
=
非平方数的平方根只能用含根号的式子表示
新知讲解
1.判断下列各式计算是否正确,并说明理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
(5)的平方根是±2 ( )
×
√
×
×
√
新知讲解
2. 下列各式是否有意义?为什么?
(1) (2) (3) (4) (5)
解(1)有意义
(2)无意义,负数没有平方根,也就没有负的平方根
(3)有意义
(4)有意义
(5)无意义,负数没有平方根
因为负数没有平方根
所以只有当时,有意义,而当时,没有意义
典例分析
例3 说出下列各式的意义,并求它们的值
(1) (2) (3) (4)
解(1)196的平方根;
(2) 的平方根;
(3)的平方根;
(4)的平方根;
典例分析
例3 说出下列各式的意义,并求它们的值
(5) (6) (7) (8)
解(5)169的正的平方根;
(6)0.0049的负的平方根;
(7)的负的平方根;
(8)的正的平方根;
变式训练
1.计算下列各式
(1)__________ (2)__________
(3)________ (4)_______
2.若则的值为_______
3.若,则的值为_______
变式训练
的平方根:表示的意义为A的正的平方根的平方根,即应先算出的值,再求其平方根
4.的平方根是________
5.的平方根是__________
6.若平方根是,则=________
变式训练
7.已知且是正数,求的值
解:由
∴
即得
∵是正数
∴
∴
拓展探究
1.已知的平方根是,的平方根是它本身,求的平方根
解:由题意可得
解得:
∴
拓展探究
2.已知的两个平方根是与,求的值.
解:由题意可得
解得:
∴的两个平方根分别和
∴
拓展探究
3.若与是数的平方根,求这个数 .
解:由题意可得当时,
解得:
∴的两个平方根分别和
∴
当时
解得:
∴是的平方根
∴
综上所述:这个数是或
拓展探究
点拨:
①若M的平方根为和
②若和是M的平方根
4.对定义运算“*”如下:
已知则求数的值
拓展探究
解:由题意得:
当时,
,
解得 (舍去)
当时,
解得或(舍去)
综上所述:
当堂检测
1.9的平方根是( )
A. B. C. D.
2.下面说法中不正确的是( )
A.4是16的平方根 B.-4是16的平方根
C.16的平方根是4 D.16的平方根是4
3.下列式子错误的是( )
A. B.
C. D.
4.的平方根分别是则的值为___
A
D
B
当堂检测
5.计算下列式子
(1)________ (2)________
(3)________ (4)________
(5)_______ (6)_______
当堂检测
6. 解方程
(1) (2)
(3) (4)
解(1)
(2)或
(3)
(4)
当堂检测
7.已知的平方根是,的平方根是,求的平方根
解:由题意可得
解得:
∴
当堂检测
8.若与是的平方根,求与这个数 .
解:由题意可得当时,
解得:
∴的两个平方根分别和
∴
当时
解得:
∴是的平方根
∴
综上所述:当时,;当时,
小结梳理
平方根
平方根的概念
平方根的表示方法
如果,那么叫做的平方根
的平方根
表示的正的平方根
表示的负的平方根
布置作业
作业:P41第1题,P42第2,3题.
谢谢观看
8.1 平方根
第1课时 平方根
第8章 实数
人教版(新教材)数学七年级下册
1.正确理解平方根的概念,会求一个数的平方根
2. 会表示一个数的平方根.
3.学生经历由特殊到一般,培养学生观察,归纳,类比的能力.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
复习引入
运算 加 减 乘 除 乘方
符号表示 + -
运算结果 和 差 积 商 幂
运算关系
完成表格信息
互为逆运算
互为逆运算
?
复习引入
+1
-1
+0.4
-0.4
0.16
1
-
+
①任何数的平方都是一个非负数
0
0
②互为相反数的两个数的平方相等
新课讲解
0
1
0.16
+1
-1
+0.4
-0.4
-
+
0
我们把0,分别叫做,的平方根
一般地,如果一个数的平方等于,那么这个数叫做的平方根或二次方根.
这就是说,如果,那么叫做的平方根.
新课讲解
互为逆运算
定义 求一个数的平方根的运算,叫做开平方.
两图中的运算有什么关系呢?
开方
平方
新课讲解
1.判断下列说法是否正确。
①是的平方根. ( )
②是的平方根. ( )
③是的平方根. ( )
④的平方根是. ( )
⑤是的一个平方根. ( )
⑥-的平方根是; ( )
⑦一个数的一个平方根是,另一个平方根一定是 ( )
×
√
√
√
×
×
√
典例讲解
例1 求下列各数的平方根:
(1) (2) (3) (4)
解(1)∵,∴的平方根是
(2)∵,∴的平方根是
(3)∵,∴的平方根是
(4)∵,∴的平方根是
注意:求一个数的平方根可将带分数化为假分数!
典例讲解
例1 求下列各数的平方根:
(5) (6) (7) (8)
解(5)∵,∴的平方根是
(6)∵,∴的平方根是
(7)∵任何数的平方都是非负数,∴没有平方根
(8)∵,∴的平方根是
典例讲解
正数 0 负数
平方根个数
平方根之间的关系
两个
1个
0个
互为相反数
0
平方根等于本身的数
0
典例讲解
例2.求下列各式中的值
(1) (2)
解(1)原式可变形为:
∵
∴或
解(2)原式可变形为:
∵
∴或
开方
解方程
变形
典例讲解
例2.解下列方程
(3) (4)
解(4)∵
∴或
解得或
解(3)原式可变形为:
∵
∴或
解得:或
思路点拨:
的值
新知讲解
的平方根表示为
=
表示的正的平方根
表示的负的平方根
读作:正负根号
表示的平方根
=
非平方数的平方根只能用含根号的式子表示
新知讲解
1.判断下列各式计算是否正确,并说明理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
(5)的平方根是±2 ( )
×
√
×
×
√
新知讲解
2. 下列各式是否有意义?为什么?
(1) (2) (3) (4) (5)
解(1)有意义
(2)无意义,负数没有平方根,也就没有负的平方根
(3)有意义
(4)有意义
(5)无意义,负数没有平方根
因为负数没有平方根
所以只有当时,有意义,而当时,没有意义
典例分析
例3 说出下列各式的意义,并求它们的值
(1) (2) (3) (4)
解(1)196的平方根;
(2) 的平方根;
(3)的平方根;
(4)的平方根;
典例分析
例3 说出下列各式的意义,并求它们的值
(5) (6) (7) (8)
解(5)169的正的平方根;
(6)0.0049的负的平方根;
(7)的负的平方根;
(8)的正的平方根;
变式训练
1.计算下列各式
(1)__________ (2)__________
(3)________ (4)_______
2.若则的值为_______
3.若,则的值为_______
变式训练
的平方根:表示的意义为A的正的平方根的平方根,即应先算出的值,再求其平方根
4.的平方根是________
5.的平方根是__________
6.若平方根是,则=________
变式训练
7.已知且是正数,求的值
解:由
∴
即得
∵是正数
∴
∴
拓展探究
1.已知的平方根是,的平方根是它本身,求的平方根
解:由题意可得
解得:
∴
拓展探究
2.已知的两个平方根是与,求的值.
解:由题意可得
解得:
∴的两个平方根分别和
∴
拓展探究
3.若与是数的平方根,求这个数 .
解:由题意可得当时,
解得:
∴的两个平方根分别和
∴
当时
解得:
∴是的平方根
∴
综上所述:这个数是或
拓展探究
点拨:
①若M的平方根为和
②若和是M的平方根
4.对定义运算“*”如下:
已知则求数的值
拓展探究
解:由题意得:
当时,
,
解得 (舍去)
当时,
解得或(舍去)
综上所述:
当堂检测
1.9的平方根是( )
A. B. C. D.
2.下面说法中不正确的是( )
A.4是16的平方根 B.-4是16的平方根
C.16的平方根是4 D.16的平方根是4
3.下列式子错误的是( )
A. B.
C. D.
4.的平方根分别是则的值为___
A
D
B
当堂检测
5.计算下列式子
(1)________ (2)________
(3)________ (4)________
(5)_______ (6)_______
当堂检测
6. 解方程
(1) (2)
(3) (4)
解(1)
(2)或
(3)
(4)
当堂检测
7.已知的平方根是,的平方根是,求的平方根
解:由题意可得
解得:
∴
当堂检测
8.若与是的平方根,求与这个数 .
解:由题意可得当时,
解得:
∴的两个平方根分别和
∴
当时
解得:
∴是的平方根
∴
综上所述:当时,;当时,
小结梳理
平方根
平方根的概念
平方根的表示方法
如果,那么叫做的平方根
的平方根
表示的正的平方根
表示的负的平方根
布置作业
作业:P41第1题,P42第2,3题.
谢谢观看
同课章节目录
