【2025春新教材】人教版七年级下册数学8.1平方根(第2课时算术平方根)课件(共32张PPT)
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学8.1平方根(第2课时算术平方根)课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 19:42:31 | ||
图片预览









文档简介
(共32张PPT)
8.1 平方根
第2课时 算数平方根
第8章 实数
人教版(新教材)数学七年级下册
1.理解算术平方根的概念,会用根号表示一个数的算术平方根;
2.根据算术平方根的概念求出非负数的算术平方根;
3.了解算术平方根的性质,并用其解题.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
复习引入
平方根
正的平方根
负的平方根
算术平方根
1.求下列各数的平方根
新知讲解
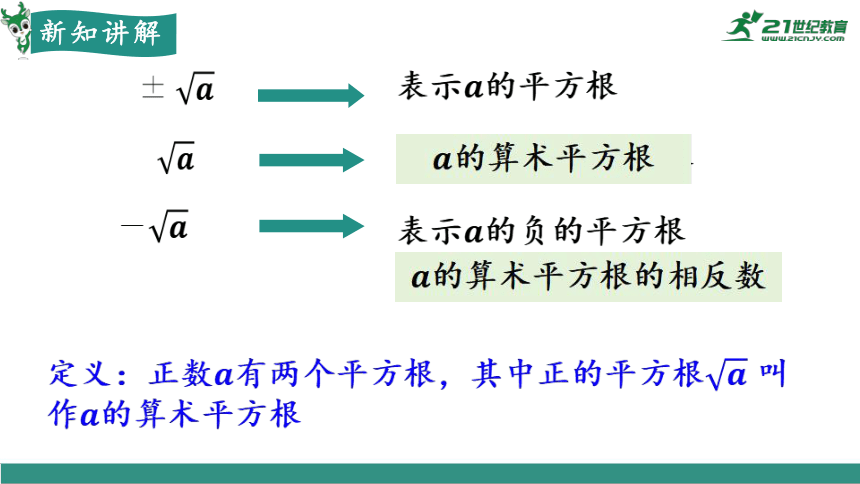
表示的正的平方根
表示的负的平方根
表示的平方根
的算术平方根
的算术平方根的相反数
定义:正数有两个平方根,其中正的平方根 叫作的算术平方根
新知讲解
1.判断下列说法是否正确.
(1) -7是49的平方根,7是49的算术平方根 ( )
(2)是的算术平方根 ( )
(3)的算术平方根是4 ( )
(4)5是的算术平方根 ( )
(5)的算术平方根的相反数是 ( )
×
√
×
×
√
典例讲解
例1 求下列各数的算术平方根:
(1) (2) (3) (4)
解(1)∵,∴的算术平方根是
(2)∵,∴的算术平方根是
(3)∵,∴的算术平方根是
(4)∵,∴的算术平方根是
典例讲解
例1 求下列各数的算术平方根:
(5) (6) (7) (8)-16
解(5)∵,∴的算术平方根是
(6)∵,∴的算术平方根是
(7)∵,∴的算术平方根是
(8)∵任何数的平方都是非负数, ∴-16没有算术平方根
1.正数的算术平方根是个正数,0的算术平方根是0,负数没有算术平方根;
2.被开方数越大,其算术平方根也越大
典例讲解
归纳总结
平方根等于本身的数是 ,
算术平方根等于它本身的数是 ,算术平方根和平方根相等的数是 ;
典例讲解
1.平方根包括算术平方根,算术平方根是平方根中非负的那一个.
2.存在条件相同.只有非负数才有平方根和算术平方根.
3.0的平方根和算术平方根均为0
正数的算术平方根有一个
正数的平方根有两个
如果一个数的平方等于,这个数就叫做的平方根
符号不同
个数不同
定义不同
联系
区
别
算术平方根
平方根
用表示
用表示
正的平方根叫作的算术平方根(0的算术平方根是0)
针对训练
1.说出下列各式的意义,并求它们的值
(1) (2) (3) (4) (5)
解(1) 的算术平方根,
(2)的算术平方根,
(3)的平方根,
(4)的算术平方根的相反数,
(5)-3的平方的算术平方根,
针对训练
解:(1)原式;
(2)原式
(3)原式
2.计算下列各式的值
(1)
(2)
(3)
针对训练
3.填空(1)若的平方根为则的算术平方根为_____
(2)若是的算术平方根,是的负平方根
则的算术平方根为________
(3)如果,那么 =_____
(4)如果的算术平方根等于2,那么
(5)若,= ;
是一种运算符号,有根号时,要先算带根号的.
变式训练
1.已知的平方根是,的算术平方根是,求的算术平方根.
解:由题意可得,
解得:
∴
变式训练
2.已知的算术平方根是其本身,的算术平方根是,求的算术平方根.
解:由题意得:,解得
∵算术平方根是其本身的数是和
∴当时
解得:
∴ ,∴
变式训练
2.已知的算术平方根是其本身,的算术平方根是,求的算术平方根.
解:当时
解得:
∴
∴
综上所述: 的算术平方根是或
新知讲解
算术平方根具有双重非负性
的算术平方根
结果为非负数
被开方数为非负数
典例讲解
例2.已知:,求的值
解:由题意得:
解得:
∴
几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂(n为正整数)及一个数的算术平方根.
针对训练
1.已知与互为相反数,求的算术平方根
解:由题意可得
∴
解得
∴
∵
∴ 的算术平方根是
拓展探究
1.已知,求的算术平方根.
解:∵ 和都为非负数
∴
∴
∴
拓展探究
2.若,求的值
解:由题意可得:
∵为非负数(即减数小于被减数)
∴
∴
∴
∴
∴
当堂测试
A
1.数的算术平方根是( )
A. B. C. D.
2.下列说法正确的是( )
A.表示的算术平方根
B.表示的算术平方根
C.的算术平方根记作
D.是的算术平方根
A
当堂测试
3.计算
(1)256的平方根___________;算术平方根__________
(2)的平方根_________;算术平方根___________
(3)的平方根_________;算术平方根_________
(4)的平方根________;算术平方根_________
注意文字或算术的表述,读清题意,再进行计算,以防误解.
当堂测试
解(1)原式.
(2)原式
(3)原式
4.计算下列各式的值
(1)
(2)
(3)
当堂测试
5.已知的平方根为的算术平方根为
(1)求的值
(2)求的算术平方根
解(1)由题意可得:
解得:
(2)
当堂测试
6.已知求
的值.
解:∵
∴
∴
即可得
当堂测试
7.若满足关系式求的算术平方根
解:由题意可得:
∵和为非负数
∴
∴
∴
∴
当堂测试
解:设每块地板砖的边长为.
由题意得
∴
∴
故每块地板砖的边长是.
8.用大小完全相同的块正方形地板砖,铺一间面积为60的会议室的地面,每块地板砖的边长是多少?
小结梳理
算术平方根
算术平方根的概念
算术平方根的双重非负性
正的平方根叫作的算术平方根
0的算术平方根是0
结果为非负数
被开方数为非负数
布置作业
作业:P43第1题,P44第2,3题.
谢谢观看
8.1 平方根
第2课时 算数平方根
第8章 实数
人教版(新教材)数学七年级下册
1.理解算术平方根的概念,会用根号表示一个数的算术平方根;
2.根据算术平方根的概念求出非负数的算术平方根;
3.了解算术平方根的性质,并用其解题.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
复习引入
平方根
正的平方根
负的平方根
算术平方根
1.求下列各数的平方根
新知讲解
表示的正的平方根
表示的负的平方根
表示的平方根
的算术平方根
的算术平方根的相反数
定义:正数有两个平方根,其中正的平方根 叫作的算术平方根
新知讲解
1.判断下列说法是否正确.
(1) -7是49的平方根,7是49的算术平方根 ( )
(2)是的算术平方根 ( )
(3)的算术平方根是4 ( )
(4)5是的算术平方根 ( )
(5)的算术平方根的相反数是 ( )
×
√
×
×
√
典例讲解
例1 求下列各数的算术平方根:
(1) (2) (3) (4)
解(1)∵,∴的算术平方根是
(2)∵,∴的算术平方根是
(3)∵,∴的算术平方根是
(4)∵,∴的算术平方根是
典例讲解
例1 求下列各数的算术平方根:
(5) (6) (7) (8)-16
解(5)∵,∴的算术平方根是
(6)∵,∴的算术平方根是
(7)∵,∴的算术平方根是
(8)∵任何数的平方都是非负数, ∴-16没有算术平方根
1.正数的算术平方根是个正数,0的算术平方根是0,负数没有算术平方根;
2.被开方数越大,其算术平方根也越大
典例讲解
归纳总结
平方根等于本身的数是 ,
算术平方根等于它本身的数是 ,算术平方根和平方根相等的数是 ;
典例讲解
1.平方根包括算术平方根,算术平方根是平方根中非负的那一个.
2.存在条件相同.只有非负数才有平方根和算术平方根.
3.0的平方根和算术平方根均为0
正数的算术平方根有一个
正数的平方根有两个
如果一个数的平方等于,这个数就叫做的平方根
符号不同
个数不同
定义不同
联系
区
别
算术平方根
平方根
用表示
用表示
正的平方根叫作的算术平方根(0的算术平方根是0)
针对训练
1.说出下列各式的意义,并求它们的值
(1) (2) (3) (4) (5)
解(1) 的算术平方根,
(2)的算术平方根,
(3)的平方根,
(4)的算术平方根的相反数,
(5)-3的平方的算术平方根,
针对训练
解:(1)原式;
(2)原式
(3)原式
2.计算下列各式的值
(1)
(2)
(3)
针对训练
3.填空(1)若的平方根为则的算术平方根为_____
(2)若是的算术平方根,是的负平方根
则的算术平方根为________
(3)如果,那么 =_____
(4)如果的算术平方根等于2,那么
(5)若,= ;
是一种运算符号,有根号时,要先算带根号的.
变式训练
1.已知的平方根是,的算术平方根是,求的算术平方根.
解:由题意可得,
解得:
∴
变式训练
2.已知的算术平方根是其本身,的算术平方根是,求的算术平方根.
解:由题意得:,解得
∵算术平方根是其本身的数是和
∴当时
解得:
∴ ,∴
变式训练
2.已知的算术平方根是其本身,的算术平方根是,求的算术平方根.
解:当时
解得:
∴
∴
综上所述: 的算术平方根是或
新知讲解
算术平方根具有双重非负性
的算术平方根
结果为非负数
被开方数为非负数
典例讲解
例2.已知:,求的值
解:由题意得:
解得:
∴
几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂(n为正整数)及一个数的算术平方根.
针对训练
1.已知与互为相反数,求的算术平方根
解:由题意可得
∴
解得
∴
∵
∴ 的算术平方根是
拓展探究
1.已知,求的算术平方根.
解:∵ 和都为非负数
∴
∴
∴
拓展探究
2.若,求的值
解:由题意可得:
∵为非负数(即减数小于被减数)
∴
∴
∴
∴
∴
当堂测试
A
1.数的算术平方根是( )
A. B. C. D.
2.下列说法正确的是( )
A.表示的算术平方根
B.表示的算术平方根
C.的算术平方根记作
D.是的算术平方根
A
当堂测试
3.计算
(1)256的平方根___________;算术平方根__________
(2)的平方根_________;算术平方根___________
(3)的平方根_________;算术平方根_________
(4)的平方根________;算术平方根_________
注意文字或算术的表述,读清题意,再进行计算,以防误解.
当堂测试
解(1)原式.
(2)原式
(3)原式
4.计算下列各式的值
(1)
(2)
(3)
当堂测试
5.已知的平方根为的算术平方根为
(1)求的值
(2)求的算术平方根
解(1)由题意可得:
解得:
(2)
当堂测试
6.已知求
的值.
解:∵
∴
∴
即可得
当堂测试
7.若满足关系式求的算术平方根
解:由题意可得:
∵和为非负数
∴
∴
∴
∴
当堂测试
解:设每块地板砖的边长为.
由题意得
∴
∴
故每块地板砖的边长是.
8.用大小完全相同的块正方形地板砖,铺一间面积为60的会议室的地面,每块地板砖的边长是多少?
小结梳理
算术平方根
算术平方根的概念
算术平方根的双重非负性
正的平方根叫作的算术平方根
0的算术平方根是0
结果为非负数
被开方数为非负数
布置作业
作业:P43第1题,P44第2,3题.
谢谢观看
同课章节目录
