【2025春新教材】人教版七年级下册数学7.2.3平行线的性质(第2课时平行线的判定和性质)教学设计
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学7.2.3平行线的性质(第2课时平行线的判定和性质)教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 791.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 19:51:09 | ||
图片预览




文档简介
/ 让教学更有效 高效备课 | 数学学科
7.2.3 平行线的性质(第2课时 平行线的判定和性质)
教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第七章“相交线与平行线”7.2.3平行线的性质(第二课时),内容包括:进一步熟悉平行线的判定方法和性质;运用平行线的判定方法和性质进行简单的推理和计算.
2.内容解析
本节课的学习是通过对例题、练习的分析和解决,巩固平行线的判定方法和性质的应用,培养学生的推理能力,渗透分析问题的方法和转化思想.
基于以上分析,确定本节课的教学重点为:熟练应用平行线的判定方法和性质定理解决问题.
二、目标和目标解析
1.目标
(1)进一步熟悉平行线的判定方法和性质;运用平行线的判定方法和性质进行简单的推理和计算.
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养学生的逻辑思维能力和创新意识.
(3)体会数学知识之间的内在联系,感受数学的逻辑性和系统性,培养几何直观和数学建模的核心素养.
2.目标解析
(1)学生能够清晰阐述平行线的定义,关于平行线的基本事实的推论、平行线的判定方法以及性质定理.在进行推理计算时步骤规范、条理清晰.
(2)对于例题和练习,学生能够仔细分析题目中的已知条件,包括直线的平行关系、角的度数或角之间的关系等信息,确定问题的类型(是利用判定还是性质来解题).在分析过程中,理解如何将复杂的几何图形和条件转化为熟悉的平行线判定和性质的应用场景,体会转化思想在解决问题中的关键作用.
(3)学生在学习过程中,能够认识到平行线的判定和性质并非孤立的知识点,而是相互关联、相互依存的.两者共同构建了关于平行线与角关系的完整知识体系.在根据图形直观地感知角与直线的关系的过程中培养几何直观能力,在将几何问题抽象为平行线模型的过程中,锻炼数学建模能力.
三、教学问题诊断分析
1.概念和定理的理解和区分
(1)同位角、内错角和同旁内角的概念较为相似,学生在识别过程中容易出现误判.
(2)平行线的判定方法和性质定理是互逆的,两者高度相似,学生在解决问题的过程中,极易将两者混淆.
2.推理过程与逻辑思维
(1)学生在书写推理过程时,可能存在跳步、因果关系不明确等问题.
(2)部分学生缺乏对问题的整体规划和分析能力,不能将各个知识点有机地整合到解题过程中.
3.数学思想方法的应用
(1)部分学生对转化思想的理解和掌握程度较低,缺乏运用数学思想方法解决问题的意识和能力.
(2)学生在从复杂的几何问题中提取出平行线的要素和关系,建立平行线模型并运用平行线知识解决时存在较大困难.
针对以上教学问题诊断分析,在教学过程中应加强对概念的深入讲解和对比练习,注重推理过程的示范和训练,强化数学思想方法的渗透和应用.
基于以上分析,确定本节课的教学难点为:综合分析问题并规范书写推理过程.
四、教学过程设计
(一)复习引入
问题1 哪些方法可以证明两条直线平行?
答 1.平行线的定义
在同一平面内,不相交的两条直线互相平行.
2.关于平行线的基本事实的推论
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
3.平行线的判定
(1)同位角相等,两直线平行.
(2)内错角相等,两直线平行.
(3)同旁内角互补,两直线平行.
问题2 平行线的性质有哪些?
答 平行线的性质有:
(1)两直线平行,同位角相等.
(2)两直线平行,内错角相等.
(3)两直线平行,同旁内角互补.
问题3 对比平行线的判定方法和性质,你能说出它们的区别和联系吗?
设计意图:复习回顾平行线的判定和性质并分析两者之间的区别与联系,第一可以加强知识的连贯性,帮助学生构建完整的知识体系.第二可以为新知识的学习提供必要的知识储备,使学生在学习新知识时更容易理解和接受.第三可以帮助学生养成复习回顾的习惯,让学生学会自主梳理知识,总结归纳学习要点.
(二)典例分析
例3 如图,已知直线a∥b,∠1=∠3,那么直线c与d平行吗?为什么?
转化1:c∥d←∠2=∠3←∠1=∠2←a∥b
解:直线c与d平行.理由如下:
如图,∵a∥b,
∴∠1=∠2(两直线平行,内错角相等).
又 ∠1=∠3,
∴∠2=∠3,
∴c∥d(同位角相等,两直线平行).
追问 你能用其他方法判定直线c与d平行吗?
转化2:c∥d←∠3=∠4←∠1=∠4←a∥b
解:直线c与d平行.理由如下:
如图,∵a∥b,
∴∠1=∠4(两直线平行,同位角相等).
又 ∠1=∠3,
∴∠3=∠4,
∴c∥d(内错角相等,两直线平行).
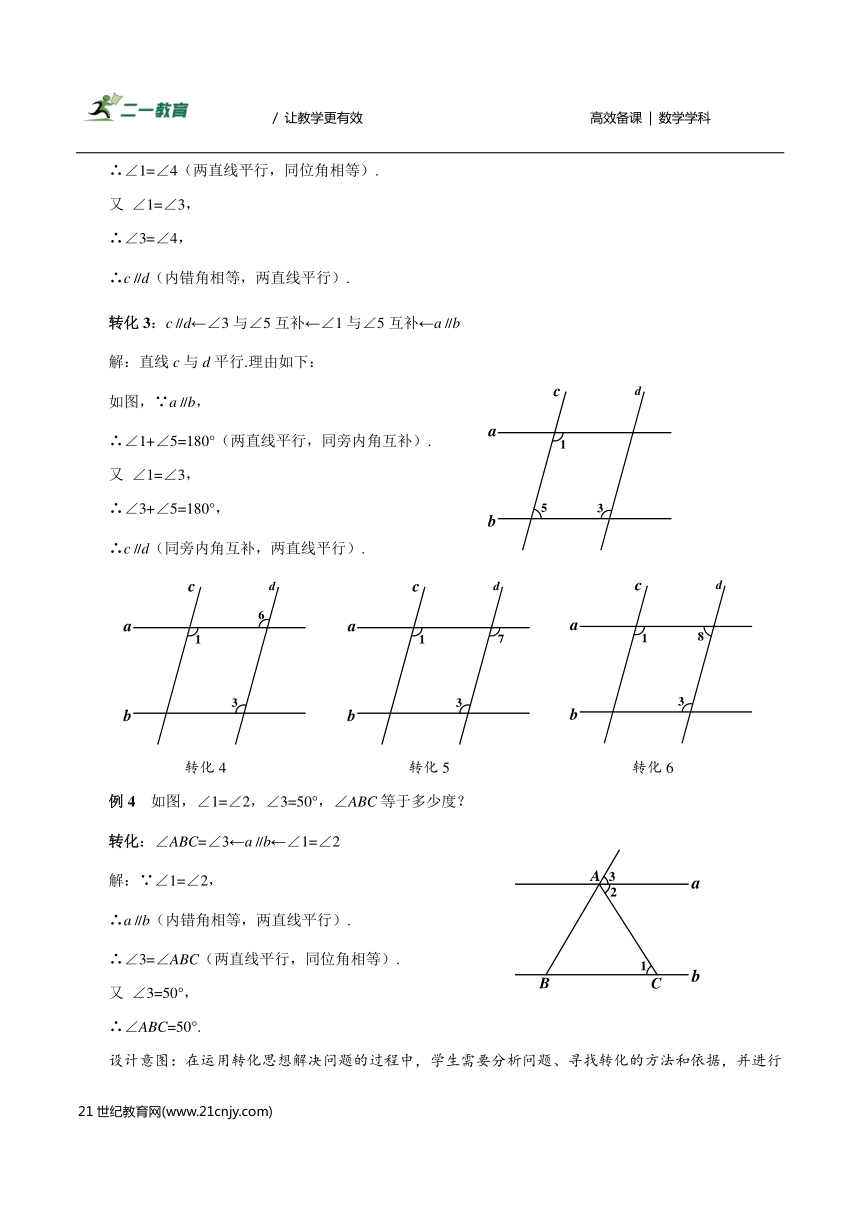
转化3:c∥d←∠3与∠5互补←∠1与∠5互补←a∥b
解:直线c与d平行.理由如下:
如图,∵a∥b,
∴∠1+∠5=180°(两直线平行,同旁内角互补).
又 ∠1=∠3,
∴∠3+∠5=180°,
∴c∥d(同旁内角互补,两直线平行).
转化4 转化5 转化6
例4 如图,∠1=∠2,∠3=50°,∠ABC等于多少度?
转化:∠ABC=∠3←a∥b←∠1=∠2
解:∵∠1=∠2,
∴a∥b(内错角相等,两直线平行).
∴∠3=∠ABC(两直线平行,同位角相等).
又 ∠3=50°,
∴∠ABC=50°.
设计意图:在运用转化思想解决问题的过程中,学生需要分析问题、寻找转化的方法和依据,并进行严谨的推理和论证,这有助于培养他们的逻辑思维能力.转化思想鼓励学生从不同的角度去思考问题,尝试用不同的方法进行转化,这有利于激发学生的创新思维,培养他们的创造力.当学生运用转化思想成功解决了原本认为困难的问题时,会获得成就感,从而增强学习数学的信心.这种成功的体验会进一步激发他们对数学学习的兴趣和积极性.
(三)巩固练习
1. 如图,如果直线a∥b,∠1+∠2=180°,那么直线b和c平行吗?为什么?
转化1:b∥c←∠3+∠2=180°←∠1=∠3←a∥b
解:直线b与c平行.理由如下:
∵a∥b,
∴∠1=∠3(两直线平行,同位角相等).
又 ∠1+∠2=180°,
∴∠3+∠2=180°,
∴b∥c(同旁内角互补,两直线平行).
追问 你能用其他方法判定直线b与c平行吗?
转化2:b∥c←∠4=∠2←∠1+∠4=180°←a∥b
解:直线b与c平行.理由如下:
∵a∥b,
∴∠1+∠4=180°(两直线平行,同旁内角互补).
又 ∠1+∠2=180°,
∴∠4=∠2,
∴b∥c(同位角相等,两直线平行).
转化3:b∥c←a∥c←∠1+∠2=180°
解:直线b与c平行.理由如下:
∵∠1+∠2=180°,
∴a∥c(同旁内角互补,两直线平行).
又 a∥b,
∴b∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
2. 如果AB∥CD,且∠1=∠2,那么直线BE与CF平行吗?为什么?
转化: BE∥CF←∠3=∠4←∠ABC=∠DCB←AB∥CD
解:直线BE与CF平行.理由如下:
∵AB∥CD,
∴∠ABC=∠DCB(两直线平行,内错角相等),
又 ∠1=∠2,
∴∠ABC-∠1=∠DCB-∠2,
∴∠3=∠4,
∴BE∥CF(内错角相等,两直线平行).
3. 找出图中互相平行的直线和互相垂直的直线.
追问 你能证明这些结论吗?请将证明过程写在作业本上.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
(四)归纳总结
1. 本节课解决问题的过程中,转化思想起到了关键作用.
2. 在初中数学中,常用的转化途径有哪些呢?
设计意图:角的数量关系与线的位置关系之间的转化,是解决平行线综合问题的核心思路,让学生深刻理解并灵活运用转化思想,能有效提升他们对平行线性质和判定的综合应用能力,帮助他们在复杂的几何问题中找到解题的突破口与方向.
转化思想能帮助学生将新知识与已有知识联系起来,既可以帮助学生深刻地理解和掌握新知识,还能帮助学生构建更加完整的知识体系.转化思想使数学学习变得更加有趣和富有挑战性,转化的意识也会对学生今后的学习产生深远的影响.
(五)感受中考
1.(2024 呼和浩特)如图,直线l1和l2被直线l3和l4所截,∠1=∠2=130°,∠3=75°,则∠4的度数为( B )
A.75° B.105° C.115° D.130°
2.(2024 陕西)如图,l1∥l2,l2∥l3,若∠1=59°,则∠2的度数为( C )
A.118° B.120° C.121° D.131°
3.(2023 鄂州)如图,直线AB∥CD,GE⊥EF于点E.若∠BGE=60°,则∠EFD的度数是( B )
A.60° B.30° C.40° D.70°
第1题图 第2题图 第3题图
4. (2024 自贡)如图,在△ABC中,DE∥BC,∠EDF=∠C.
求证:∠BDF=∠A.
证明:∵DE∥BC,
∴∠C=∠AED(两直线平行,同位角相等),
∵∠EDF=∠C,
∴∠AED=∠EDF,
∴DF∥AC(内错角相等,两直线平行),
∴∠BDF=∠A(两直线平行,同位角相等).
追问 你能用其他方法证明∠BDF=∠A吗?
5. (2022 武汉)如图,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
(2)AE平分∠BAD交BC于点E,∠BCD=50°.求证:AE∥DC.
(1)解:∵AD∥BC,
∴∠B+∠BAD=180°(两直线平行,同旁内角互补),
∵∠B=80°,
∴∠BAD=100°.
(2)证明:∵AE平分∠BAD,∠BAD=100°
∴∠DAE=∠BAD=50°.
∵AD∥BC,
∴∠AEB=∠DAE=50°(两直线平行,内错角相等),
∵∠BCD=50°,
∴∠AEB=∠BCD,
∴AE∥DC(同位角相等,两直线平行).
追问 你能用其他方法证明AE∥DC吗?
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(六)小结梳理
(七)布置作业
1.必做题:习题7.2 第7题.
2.探究性作业:
如图,许多漂亮的装饰图案是用平行条纹设计的,请你用平行条纹设计一些图案,并与同学交流一下.
21世纪教育网(www.21cnjy.com)
7.2.3 平行线的性质(第2课时 平行线的判定和性质)
教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第七章“相交线与平行线”7.2.3平行线的性质(第二课时),内容包括:进一步熟悉平行线的判定方法和性质;运用平行线的判定方法和性质进行简单的推理和计算.
2.内容解析
本节课的学习是通过对例题、练习的分析和解决,巩固平行线的判定方法和性质的应用,培养学生的推理能力,渗透分析问题的方法和转化思想.
基于以上分析,确定本节课的教学重点为:熟练应用平行线的判定方法和性质定理解决问题.
二、目标和目标解析
1.目标
(1)进一步熟悉平行线的判定方法和性质;运用平行线的判定方法和性质进行简单的推理和计算.
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养学生的逻辑思维能力和创新意识.
(3)体会数学知识之间的内在联系,感受数学的逻辑性和系统性,培养几何直观和数学建模的核心素养.
2.目标解析
(1)学生能够清晰阐述平行线的定义,关于平行线的基本事实的推论、平行线的判定方法以及性质定理.在进行推理计算时步骤规范、条理清晰.
(2)对于例题和练习,学生能够仔细分析题目中的已知条件,包括直线的平行关系、角的度数或角之间的关系等信息,确定问题的类型(是利用判定还是性质来解题).在分析过程中,理解如何将复杂的几何图形和条件转化为熟悉的平行线判定和性质的应用场景,体会转化思想在解决问题中的关键作用.
(3)学生在学习过程中,能够认识到平行线的判定和性质并非孤立的知识点,而是相互关联、相互依存的.两者共同构建了关于平行线与角关系的完整知识体系.在根据图形直观地感知角与直线的关系的过程中培养几何直观能力,在将几何问题抽象为平行线模型的过程中,锻炼数学建模能力.
三、教学问题诊断分析
1.概念和定理的理解和区分
(1)同位角、内错角和同旁内角的概念较为相似,学生在识别过程中容易出现误判.
(2)平行线的判定方法和性质定理是互逆的,两者高度相似,学生在解决问题的过程中,极易将两者混淆.
2.推理过程与逻辑思维
(1)学生在书写推理过程时,可能存在跳步、因果关系不明确等问题.
(2)部分学生缺乏对问题的整体规划和分析能力,不能将各个知识点有机地整合到解题过程中.
3.数学思想方法的应用
(1)部分学生对转化思想的理解和掌握程度较低,缺乏运用数学思想方法解决问题的意识和能力.
(2)学生在从复杂的几何问题中提取出平行线的要素和关系,建立平行线模型并运用平行线知识解决时存在较大困难.
针对以上教学问题诊断分析,在教学过程中应加强对概念的深入讲解和对比练习,注重推理过程的示范和训练,强化数学思想方法的渗透和应用.
基于以上分析,确定本节课的教学难点为:综合分析问题并规范书写推理过程.
四、教学过程设计
(一)复习引入
问题1 哪些方法可以证明两条直线平行?
答 1.平行线的定义
在同一平面内,不相交的两条直线互相平行.
2.关于平行线的基本事实的推论
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
3.平行线的判定
(1)同位角相等,两直线平行.
(2)内错角相等,两直线平行.
(3)同旁内角互补,两直线平行.
问题2 平行线的性质有哪些?
答 平行线的性质有:
(1)两直线平行,同位角相等.
(2)两直线平行,内错角相等.
(3)两直线平行,同旁内角互补.
问题3 对比平行线的判定方法和性质,你能说出它们的区别和联系吗?
设计意图:复习回顾平行线的判定和性质并分析两者之间的区别与联系,第一可以加强知识的连贯性,帮助学生构建完整的知识体系.第二可以为新知识的学习提供必要的知识储备,使学生在学习新知识时更容易理解和接受.第三可以帮助学生养成复习回顾的习惯,让学生学会自主梳理知识,总结归纳学习要点.
(二)典例分析
例3 如图,已知直线a∥b,∠1=∠3,那么直线c与d平行吗?为什么?
转化1:c∥d←∠2=∠3←∠1=∠2←a∥b
解:直线c与d平行.理由如下:
如图,∵a∥b,
∴∠1=∠2(两直线平行,内错角相等).
又 ∠1=∠3,
∴∠2=∠3,
∴c∥d(同位角相等,两直线平行).
追问 你能用其他方法判定直线c与d平行吗?
转化2:c∥d←∠3=∠4←∠1=∠4←a∥b
解:直线c与d平行.理由如下:
如图,∵a∥b,
∴∠1=∠4(两直线平行,同位角相等).
又 ∠1=∠3,
∴∠3=∠4,
∴c∥d(内错角相等,两直线平行).
转化3:c∥d←∠3与∠5互补←∠1与∠5互补←a∥b
解:直线c与d平行.理由如下:
如图,∵a∥b,
∴∠1+∠5=180°(两直线平行,同旁内角互补).
又 ∠1=∠3,
∴∠3+∠5=180°,
∴c∥d(同旁内角互补,两直线平行).
转化4 转化5 转化6
例4 如图,∠1=∠2,∠3=50°,∠ABC等于多少度?
转化:∠ABC=∠3←a∥b←∠1=∠2
解:∵∠1=∠2,
∴a∥b(内错角相等,两直线平行).
∴∠3=∠ABC(两直线平行,同位角相等).
又 ∠3=50°,
∴∠ABC=50°.
设计意图:在运用转化思想解决问题的过程中,学生需要分析问题、寻找转化的方法和依据,并进行严谨的推理和论证,这有助于培养他们的逻辑思维能力.转化思想鼓励学生从不同的角度去思考问题,尝试用不同的方法进行转化,这有利于激发学生的创新思维,培养他们的创造力.当学生运用转化思想成功解决了原本认为困难的问题时,会获得成就感,从而增强学习数学的信心.这种成功的体验会进一步激发他们对数学学习的兴趣和积极性.
(三)巩固练习
1. 如图,如果直线a∥b,∠1+∠2=180°,那么直线b和c平行吗?为什么?
转化1:b∥c←∠3+∠2=180°←∠1=∠3←a∥b
解:直线b与c平行.理由如下:
∵a∥b,
∴∠1=∠3(两直线平行,同位角相等).
又 ∠1+∠2=180°,
∴∠3+∠2=180°,
∴b∥c(同旁内角互补,两直线平行).
追问 你能用其他方法判定直线b与c平行吗?
转化2:b∥c←∠4=∠2←∠1+∠4=180°←a∥b
解:直线b与c平行.理由如下:
∵a∥b,
∴∠1+∠4=180°(两直线平行,同旁内角互补).
又 ∠1+∠2=180°,
∴∠4=∠2,
∴b∥c(同位角相等,两直线平行).
转化3:b∥c←a∥c←∠1+∠2=180°
解:直线b与c平行.理由如下:
∵∠1+∠2=180°,
∴a∥c(同旁内角互补,两直线平行).
又 a∥b,
∴b∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
2. 如果AB∥CD,且∠1=∠2,那么直线BE与CF平行吗?为什么?
转化: BE∥CF←∠3=∠4←∠ABC=∠DCB←AB∥CD
解:直线BE与CF平行.理由如下:
∵AB∥CD,
∴∠ABC=∠DCB(两直线平行,内错角相等),
又 ∠1=∠2,
∴∠ABC-∠1=∠DCB-∠2,
∴∠3=∠4,
∴BE∥CF(内错角相等,两直线平行).
3. 找出图中互相平行的直线和互相垂直的直线.
追问 你能证明这些结论吗?请将证明过程写在作业本上.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
(四)归纳总结
1. 本节课解决问题的过程中,转化思想起到了关键作用.
2. 在初中数学中,常用的转化途径有哪些呢?
设计意图:角的数量关系与线的位置关系之间的转化,是解决平行线综合问题的核心思路,让学生深刻理解并灵活运用转化思想,能有效提升他们对平行线性质和判定的综合应用能力,帮助他们在复杂的几何问题中找到解题的突破口与方向.
转化思想能帮助学生将新知识与已有知识联系起来,既可以帮助学生深刻地理解和掌握新知识,还能帮助学生构建更加完整的知识体系.转化思想使数学学习变得更加有趣和富有挑战性,转化的意识也会对学生今后的学习产生深远的影响.
(五)感受中考
1.(2024 呼和浩特)如图,直线l1和l2被直线l3和l4所截,∠1=∠2=130°,∠3=75°,则∠4的度数为( B )
A.75° B.105° C.115° D.130°
2.(2024 陕西)如图,l1∥l2,l2∥l3,若∠1=59°,则∠2的度数为( C )
A.118° B.120° C.121° D.131°
3.(2023 鄂州)如图,直线AB∥CD,GE⊥EF于点E.若∠BGE=60°,则∠EFD的度数是( B )
A.60° B.30° C.40° D.70°
第1题图 第2题图 第3题图
4. (2024 自贡)如图,在△ABC中,DE∥BC,∠EDF=∠C.
求证:∠BDF=∠A.
证明:∵DE∥BC,
∴∠C=∠AED(两直线平行,同位角相等),
∵∠EDF=∠C,
∴∠AED=∠EDF,
∴DF∥AC(内错角相等,两直线平行),
∴∠BDF=∠A(两直线平行,同位角相等).
追问 你能用其他方法证明∠BDF=∠A吗?
5. (2022 武汉)如图,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
(2)AE平分∠BAD交BC于点E,∠BCD=50°.求证:AE∥DC.
(1)解:∵AD∥BC,
∴∠B+∠BAD=180°(两直线平行,同旁内角互补),
∵∠B=80°,
∴∠BAD=100°.
(2)证明:∵AE平分∠BAD,∠BAD=100°
∴∠DAE=∠BAD=50°.
∵AD∥BC,
∴∠AEB=∠DAE=50°(两直线平行,内错角相等),
∵∠BCD=50°,
∴∠AEB=∠BCD,
∴AE∥DC(同位角相等,两直线平行).
追问 你能用其他方法证明AE∥DC吗?
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(六)小结梳理
(七)布置作业
1.必做题:习题7.2 第7题.
2.探究性作业:
如图,许多漂亮的装饰图案是用平行条纹设计的,请你用平行条纹设计一些图案,并与同学交流一下.
21世纪教育网(www.21cnjy.com)
同课章节目录
