2025年中考数学复习--动点中的隐圆问题 课件(共57张PPT)
文档属性
| 名称 | 2025年中考数学复习--动点中的隐圆问题 课件(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 23:09:12 | ||
图片预览







文档简介
(共57张PPT)
中考数学复习--动点中的隐圆问题
在中考数学中,有一些高频考题,如线段的最值问题,动点路程问题,几乎每年各地都会有出现。在这些题目中的图形中往往没有出现“圆”,但在解题时却要用到“圆”的知识点,我们把这样类型的题目称之为“隐圆模型”。
----看不见的圆
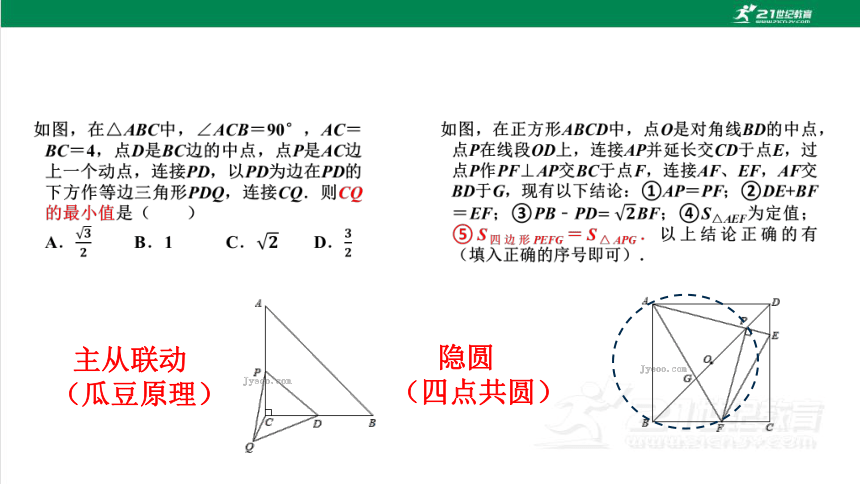
如图,在△ABC中,∠ACB=90°,AC=BC=4,点D是BC边的中点,点P是AC边上一个动点,连接PD,以PD为边在PD的下方作等边三角形PDQ,连接CQ.则CQ的最小值是( )
A. B.1 C. D.
如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF,AF交BD于G,现有以下结论:①AP=PF;②DE+BF=EF;③PB﹣PDBF;④S△AEF为定值;⑤S四边形PEFG=S△APG.以上结论正确的有 (填入正确的序号即可).
主从联动
(瓜豆原理)
隐圆
(四点共圆)
图,直尺AB垂直竖立在水平面上,将一个含45°角的直角三角板CDE的斜边DE靠在直尺的一边AB上,使点E与点A重合,DE=12cm.当点D沿DA方向滑动时,点E同时从点A出发沿射线AF方向滑动.当点D滑动到点A时,点C运动的路径长为 _______cm.
在平面直角坐标系中,直线y=﹣x﹣2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a>0)经过A,B两点,并与x轴的正半轴交于点C.
(1)求a,b满足的关系式及c的值;
(2)当a时,若点P是抛物线对称轴上的一个动点,求△ABP周长的最小值;
(3)当a1时,求QD的最大值。
点C在∠BAF的平分线上运动
将
军
饮
马
构
造
二
次
函
数
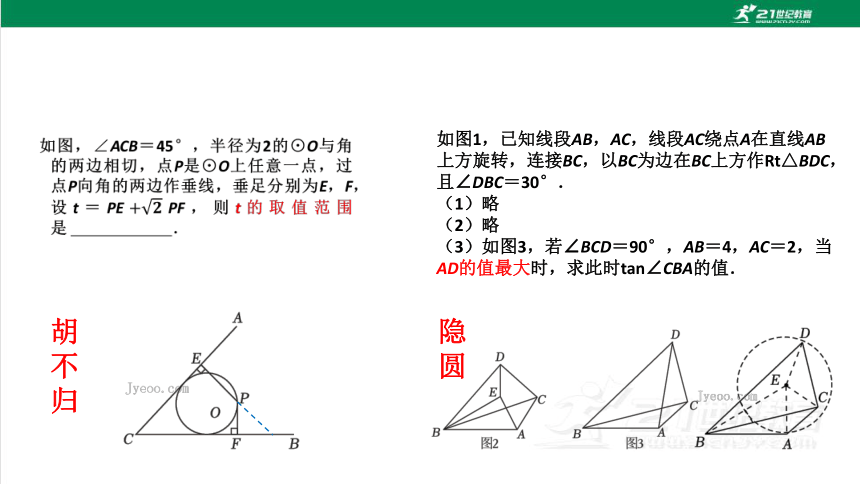
如图,∠ACB=45°,半径为2的⊙O与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设t=PEPF,则t的取值范围是 .
如图1,已知线段AB,AC,线段AC绕点A在直线AB上方旋转,连接BC,以BC为边在BC上方作Rt△BDC,且∠DBC=30°.
(1)略
(2)略
(3)如图3,若∠BCD=90°,AB=4,AC=2,当AD的值最大时,求此时tan∠CBA的值.
胡
不
归
隐
圆
如图,在△ABC中,AB=5,tan∠C=2,则ACBC的最大值为 .
在平面直角坐标系xOy中,已知抛物线F:y=﹣x2+bx+c经过点A(﹣3,﹣1),与y轴交于点B(0,2).
(1)求抛物线的函数表达式;
(2)在直线AB上方抛物线上有一动点C,连接OC交AB于点D,求的最大值及此时点C的坐标;
胡不归+定角定边
构造二次函数
模型背景
定
角
定
边
定
角
定
边
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足ADCE,则下列结论:①;②∠DFE=135°;③△ABF面积的最大值是44;④CF的最小值是22.其中正确的是( )
A.①③ B.①②④ 、
C.②③④ D.①②③④
如图是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成.在正方形ABCD中,AB=10.下列三个结论:①若tan∠ADF,则EF=2;②若Rt△ABG的面积是正方形EFGH面积的3倍,则点F是AG的三等分点;③将△ABG绕点A逆时针旋转90°得到△ADG',则BG′的最大值为55.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
阿氏圆
定角定高
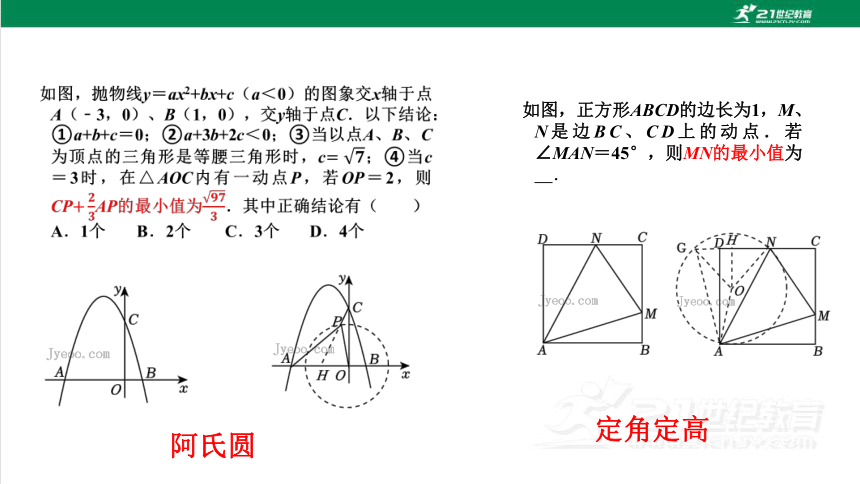
如图,抛物线y=ax2+bx+c(a<0)的图象交x轴于点A(﹣3,0)、B(1,0),交y轴于点C.以下结论:①a+b+c=0;②a+3b+2c<0;③当以点A、B、C为顶点的三角形是等腰三角形时,c;④当c=3时,在△AOC内有一动点P,若OP=2,则CPAP的最小值为.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
如图,正方形ABCD的边长为1,M、N是边BC、CD上的动点.若∠MAN=45°,则MN的最小值为 .
定点定长
定角定边
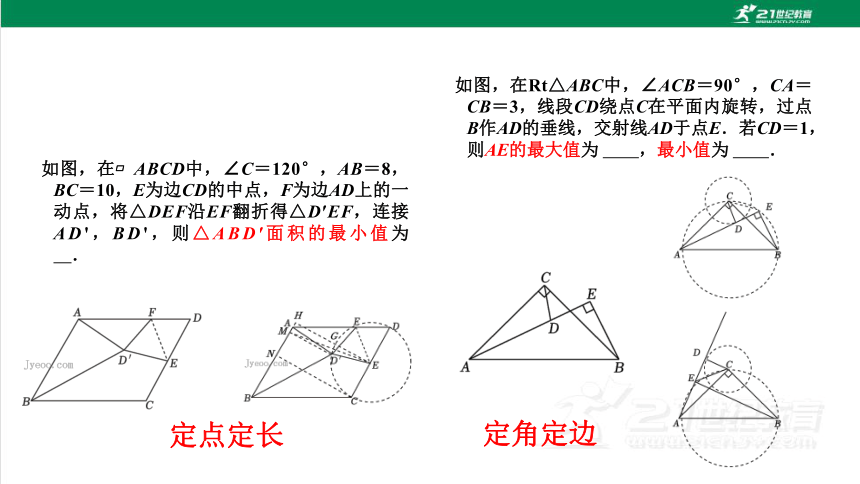
如图,在 ABCD中,∠C=120°,AB=8,BC=10,E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,连接AD',BD',则△ABD′面积的最小值为 .
如图,在Rt△ABC中,∠ACB=90°,CA=CB=3,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E.若CD=1,则AE的最大值为 ,最小值为 .
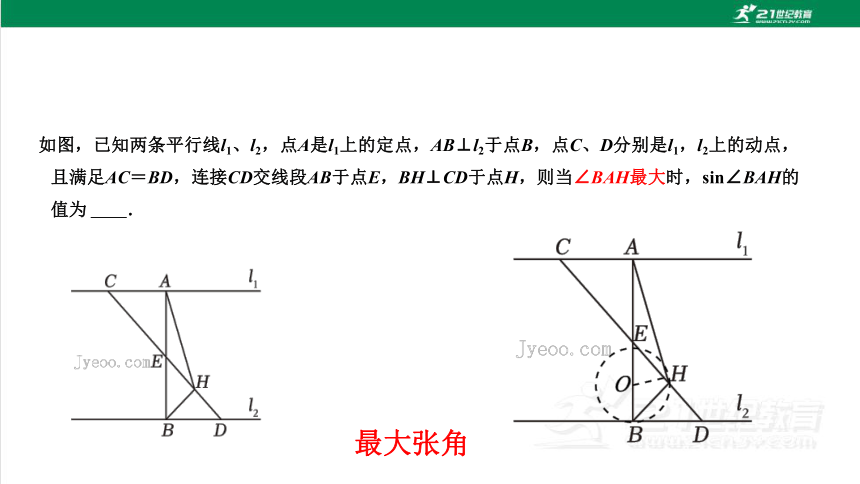
最大张角
如图,已知两条平行线l1、l2,点A是l1上的定点,AB⊥l2于点B,点C、D分别是l1,l2上的动点,且满足AC=BD,连接CD交线段AB于点E,BH⊥CD于点H,则当∠BAH最大时,sin∠BAH的值为 .
模型背景
三、顺应《课程标准》
《课标》课程理念要求:课程目标以学生发展为本,以核心素养为导向,进一步获得数学基础知识、基本技能、基本思想和基本经验(简称“四基”),发展运用数学知识与方法发现、提出、分析和解决问题的能力(简称“四能”),形成正确的情感、态度和价值观。
模型背景
三、顺应《课程标准》
课程目标要求:初中阶段,核心素养主要表现为:抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识,创新意识。
模型背景
三、顺应《课程标准》
课程内容要求:第四学段(7-9年级)掌握(节选)
图形的性质
①掌握基本事实:两点之间线段最短;
②理解垂线段的概念;
③理解圆、弧、弦、圆心角、圆周角的概念。
模型背景
三、顺应《课程标准》
学业质量标准:第四学段(7-9年级)(节选)
知道运动过程的不变量、图形运动的变化特征,能运用几何图形的基本性质进行推理证明。
模型背景
三、顺应《课程标准》
学业水平考试:第四学段(7-9年级)(节选)
适当提高应用性、探究性和综合性试题比例,题目设置要注重创新真实情境,提出有意义的问题,实现核心素养导向的义务教育数学课程学业质量的全面考查。
有“圆” 千里来相会,无“圆” 对面不相识
寻找圆的“影子”, 使得“圆” 形毕露
常见的隐圆模型
模型1:定点定长型
动点P到定点0的距离为d保持不变,则点P的轨迹为以点0为圆心,d为半径的圆弧.
圆的定义:圆是到定点的距离等于定长的点的集合。
o
P
d
模型1:定点定长型
若AB=AC=AD.则点B、C、D在以A为圆心,AB为半径的圆上。
1.几个点到某个定点距离相等可用圆(定点为圆心,相等距离为半径)
模型1:定点定长型
1.几个点到某个定点距离相等可用圆(定点为圆心,相等距离为半径)
例1.如图,已知AB=AC=AD,∠CBD=2 ∠ BDC, ∠ BAC=44°,则∠ CAD的度数为_____.
模型1:定点定长型
例2.在矩形ABCD中,已知AB=2cm,BC=3cm,现有一根长为2cm的木棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为多少?
2.动点到定点距离保持不变的可用圆
方法:先确定定点,定点为圆心,动点到定点的距离为半径。
A
B
D
C
E
F
P
S=2x3-πx
=6-π
A
B
D
C
E
F
P
模型1:定点定长型
2.动点到定点距离保持不变的可用圆
例3.如图,矩形ABCD中,AB=2,AD=3,点E、F分别为AD、DC边上的点,
且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为____
分析:
PA+PG=PA'+PG≥A'G
A'G的最小值为
A'D-DG=5-1=4
A’
一箭穿心
模型1:定点定长型
3.过定点作折叠的可用圆(定点为圆心,对应点到定点的距离为半径)
例4.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是____
【分析】考虑△AMN沿MN所在直线翻折得到△A'MN,可得MA'=MA=1,所以A'轨迹是以M点为圆心,MA为半径的圆弧,连接CM,与圆的交点即为所求的A',此时A'C的值最小,构造直角△MHC,勾股定理求CM,再减去A'M即可.
模型1:定点定长型
3.过定点作折叠的可用圆(定点为圆心,对应点到定点的距离为半径)
例5.如图,在Rt △ABC中, ∠ C=90°,AC=6,BC=8,点F在边AC上,并
且CF=2,点E为边BC上的动点,将△ CEF沿直线EF翻折,点C落在点P处
则点P到边AB距离的最小值是 _____.
【分析】考虑到将△ FCE沿
EF翻折得到△ FPE,可得P点轨迹是以F点为圆心,FC为半径的圆弧:过F点作FH⊥AB,与圆的交点即为所求P点,此时点P到AB的距离最小,由相似或三角函数先求FH,再减去FP,即可得到PH.
一箭穿心+垂线段最短
模型1:定点定长型
例6.如图,矩形ABCD中,AB=4,BC=8,P、Q分别是直线BC、AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△ FEQ,连接PF、PD,则PF+PD的小值是_______.
【分析】F点轨迹是以E点为圆心,EA为半径的圆,作点D关于BC对称点D',连接PD',PF+PD化为PF+PD'.连接ED',与圆的交点为所求F点,与BC交点为所求P点,勾股定理先求ED'再减去EF即可
D'
3.过定点作折叠的可用圆(定点为圆心,对应点到定点的距离为半径)
模型1:定点定长型
4.“瓜豆”里的隐圆(主从联动型,主动点轨迹为圆则从动点的轨迹也是圆)
例7.(泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
解析:
连接AB,取 AB的中点E,连接EM.易得EM 为△ABC的中位线,
EM=BC=1,OE=
OM 的最大值为 EM+OE= + .故选 B
主动点--定点定长型 从动点--定点定长型
E
(瓜豆)微课
A.C.2
模型1:定点定长型
方法二:作点A关于y轴的对称点
例7.(泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.C.2
模型1:定点定长型
4.“瓜豆”里的隐圆(主从联动型,主动点轨迹为圆则从动点的轨迹也是圆)
例8.如图,AB=4,0为AB的中点, ⊙0的半径为1,点P是⊙0上一动点,
以点P为直角顶点的等腰直角△PBC(点P,B,C按逆时针方向排列),则线
段AC长的取值范围是 ____
O '
分析:连接O ‘C,连接OP,易得∠OBP=∠ O B‘C,所以 所以 O ‘C ,所以点C在以O ‘为圆心, 为半径的圆上运动,可求得A O ‘=2 ,因此AC的最大值为+ ,AC的最小值为 ,所以线段AC长的取值范围是 .
模型2:直角对直径
原理:圆O中,圆周角是90°所对的弦是直径。
固定线段AB所对动角∠C恒为90°,则A、B、C三点共圆,AB为直径。
A
B
C(动点)
A
B
C(动点)
模型2:直角对直径
例9.在正方形ABCD中,AD=2,E,F分别为边DC,CB上的点,且始终保持DE=CF,连接AE和DF交于点P,则线段CP的最小值为_____.
【解析】
如图,在△ADE和△ DCF中,AD=DC,
∠ADE=∠DCE,DE=DF
∴ △ ADE△ DCF(SAS)
∴∠DAE=∠CDF
∴∠DAE+∠AED=90°
∴∠CDF+∠AED=90°
∠APD=90 °保持不变
∴点 P的轨迹为以 AD为直径的一段弧上
取 AD 中点 2,连接 C,与该圆弧交点即为点 P,此时 CP值最小,在 Rt△CQD中,CQ=5,CP=CQ-PQ=
模型2:直角对直径
例10.如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF,连接CF交BD于点G,连接BE交AG于点H,若正方形边长为2,则线段DH长度的最小值是____.
【分析】
根据条件可知:∠DAG=∠DCG=∠ABE
易证AG⊥BE,即∠AHB=90°,
所以H点轨迹是以AB为直径的圆弧
当D、H、0共线时,DH取到最小值
勾股定理可求,答案为-1
o
模型2:直角对直径
例11.如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=10,点D是AC上的一
个动点,以CD为直径作圆O,连接BD交圆O于点E,则AE的最小值_____.
【分析】
连接 CE,由于 CD为直径,故∠CED=90°,考虑到 CD 是动线段,故可以将此题看成定线段 CB 对直角∠CEB.取 CB 中点 M,所以E点轨迹是以M为圆心、CB为直径的圆弧,连接AM,与圆弧交点即为所求 E点,此时E值最小,AE=AM-EM=2-2.
模型3:定边对定角
模型解读
定边对定角微课
P(动)
固定线段AB所对动角P为定值则点P运动轨迹为过A、B、C三点的圆
P(动)
原理:弦AB所对同侧圆周角恒相等备注:点P在优弧、劣弧上运动皆可
模型3:定边对定角
例12.如图,等边△ABC边长为2,E、F分别是BC、CA上两个动点,且BE=CF,连接AE、BF,交点为P点,则CP的最小值为________.
【分析】由BE=CF可推得三角形ABE≌三角形BCF,所以∠APF=60°但∠APF所对的边AF是变化的:所以考虑∠APB=120°,其对边AB是定值。所以如图所示,P点轨迹是以点O为圆心的圆弧。(构造OA=OB且∠AOB=120°)当0、P、C共线时,可得CP的最小值,利用Rt△OBC勾股定理求得OC,再减去OP即可.
O
模型3:定边对定角
例13.如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P从点P向半径0A引垂线PH交OA于点H,设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为________.
C
分析:由内心的性质可得∠PIO=135°
连接AI,∵OI平分∠AOP,OP=OA
∴ △AIO△PIO,
∴ ∠AIO=∠PIO=135°
∵ OA为定边,∠AIO=135°为定角
∴ 点P在以OA为弦且圆心角为90°的圆弧上运动
记圆心为点C,易求得
由弧长公式可求得圆心I的运动路径长.
模型3:定边对定角
例14.如图,已知以AB为直径的圆O,C为弧AB的中点,P为弧BC上任意一点,CD垂直CP交AP于D,连接BD,若AB=6.则BD的最小值为_____.
分析:
连接 AC,易得∠P=45°,所以△CDP为等腰直角三角形,
∴∠ADC=135°为定角,AC为定边。
∴圆心角∠AGC=90 °
∵AB=6,∴AC=,∴AG=CG=3
∴BG= =
G
例14.如图,已知以AB为直径的圆O,C为弧AB的中点,P为弧BC上任意一点,CD垂直CP交AP于D,连接BD,若AB=6.则BD的最小值为_____.
“瓜豆”分析--构造“双子型(手拉手模型)”
连接0C,作CG⊥CO,且 CG=C0,连接 0G,OP,易证得COP≌CGD,∴GD=0P=3,为定值。
点D在以G为圆心3为半径的圆弧上。可求得 BG= =
G
方法二:定点定长型
模型4:定角夹定高
【题型背景】
在一些最值问题中,给定一个角,并且过定角的顶点作对边的垂线为定值时,也存在最值问题,面对这种问题我们借助“隐圆”进行说明:我们称这种问题为:“定角夹定高”模型也成“探照灯”模型。
主要解决:(1)线段最短问题:(2)面积最小问题。
[模型]
如右图所示,在△ABC中,∠BAC=为定值,AD为BC边上的高,且AD=h为定值,则底边BC存在最小值,△ABC面积存在最小值, △ABC周长存在最小值。
模型4:定角夹定高
【模型]如右图所示,在三角形ABC中,∠BAC=为定值,AD为BC边上的高且AD=h为定值,则底边BC存在最小值,△ABC面积存在最小值.
[解题突破点]
1.找出“隐圆”——三角形外接圆
2.定高过外心(半径+弦心距>定高),即AB=AC(等腰三角形)
定角定高微课
模型4:定角夹定高
分析:当高经过外心时,BC最小,此时AB=AC,且∠A=60°,所以ABC为等边三角形,所以可得BC=6.
r
例15.如图在△ABC中,∠A=60°,BC边上的高为求BC的最小值。
∵
∴
∴
∴
模型4:定角夹定高
例16.如图,在四边形ABCD中,AB=AD=CD=4,ADBC,∠B=60°,点E、F分别为边BC、CD上的两个动点,且∠EAF=60°,则AEF的面积是否存在最小值 若存在,求出其最小值;若不存在,请说明理由。
F '
O
H
G
分析:如图,将△ADF绕点A顺时针旋转120°到△ABF′,则∠EAF′=60°
易证△AEF≌△AEF′ ,作△AE F′的外接圆⊙O,作OH⊥BC于点H,AG⊥BC于点G,
则∠F′OH=60°,AG,
设⊙O的半径为r,则OH,
∵OA+OH,∴,∴,
∵∠FAE=∠F′AE=∠FOE=60°
∴F′E=
∴S△AEF=S△AEF′EF′ AG,
∴△AEF面积的最小值是4.
模型4:定角夹定高
周长的最小值
某地举办了迎新年大型灯光秀表演.其中一个镭射灯距城墙30米,镭射灯发出的两根彩色光线夹角为60°,如图,若将两根光线(AB,AC)和光线与城墙的两交点的连接的线段(BC)看作一个三角形,记为△ABC,那么该三角形周长有没有最小值?若有,求出最小值,若没有,说明理由.
延长CB至点D,使BD=BA,连接AD,
延长BC至点E,使CE=AC,连接AE。
D
E
当点A、F、G、O四点共线时,半径r最小,r,故DE最小。
解题突破点:AB=AC时,周长最小。
O
F
G
模型4:定角夹定高
定角夹定中线
定角夹定角平分线
中线倍长 定边对定角
作双高 定角夹定高
突破点:AB=AC时,△ABC面积有最大值
突破点:AB=AC时,△ABC面积有最小值
模型5:四点共圆
四点共圆的基本图形
A
B
C
D
C
D
B
A
[对角互补型]
如图,∠A+∠C=180°或∠B+∠D=180°,
则A、B、C、D四点共圆。
[同侧等角型]
如图,∠A=∠C,则A、B、C、D四点共圆。
模型5:四点共圆
例17.如图,在正方形ABCD中,0为AC、BD的交点,△DCE为直角三角形∠CED=90°,∠DCE=30°,若 ,则正方形ABCD的面积为____.
F
分析:过点D作DF⊥OE于点F,设DF=x,则EF=x,OF=
∴
∴
∴
∴
模型5:四点共圆
o
例18.如图,等边△ABC中,AB=6,P为AB边上一动点,PD⊥BC,PE ⊥AC,则DE的最小值为____.
:∵ ∠PEC=∠PDC=90°,
∴ P、D、C、E四点共圆,且CP为直径,O为圆心
∴ ∠EOD=2∠ACB=120°,
∴ DE=要使DE最小,则⊙O的半径r最小,故直径PC最小。
当CP⊥AB时,
∴,,
∴.
模型5:四点共圆
2.手拉手(双子型)中的四点共圆
条件:△0CD∽△0AB
结论:
① △ 0AC ∽ △ 0BD:
②AC与BD交于点E,必有∠AEB=∠AOB;
③点E在△0AB的外接圆上.即O、A、B、E四点共圆. 同理:O、D、C、E也四点共圆.
模型5:四点共圆
2.手拉手(双子型)中的四点共圆
例19.如图①,在钝角△ABC中,∠ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将△ BDE绕点B逆时针方向旋转a度(0大于a小于180);
(1)如图②,当0(2)如图③,直线CE、AD交于点G.在旋转过程中,∠AGC的大小是否发生变化
如变化,请说明理由;如不变,请求出这个角的度数;
(3)将△BDE从图①位置绕点B逆时针方向旋转180°,求点G的运动路程
模型5:四点共圆
例19.如图①,在钝角ABC中,∠ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将BDE绕点B逆时针方向旋转a度(0a≤180)
(1)如图②,当0(2)如图③,直线CE、AD交于点G.在旋转过程中,∠AGC的大小是否发生变化
如变化,请说明理由;如不变,请求出这个角的度数;
(3)将ΔBDE从图①位置绕点B逆时针方向旋转180°,求点G的运动路程.
H
K
的长
点G的运动路程是的长的两倍.
米勒(Johannes Miier 1436--1476)德国数学家,对三角做出了巨大贡献,是欧洲最有影响的数学家之一。米勒发表的《三角全书》,是使得三角学在欧洲取得独立地位的第一部系统性著作。
1471年,米勒提出了一个有趣的问题:在地球表面什么部位,一根垂直的悬杆呈现最长 即在什么部位,视角最大 最大视角问题是数学史上100个著名的极值问题之一。
模型6:“米勒问题”之最大张角
米勒问题一般的描述是:
已知,点A、B是∠MON的OM边上的两个定点,C是ON边上的一个动点,当C在何处时,∠ACB最大
问题解决:
当且仅当△ABC的外接圆与边ON
相切于点C时,角ACB最大。
模型6:“米勒问题”之最大张角
最大张角微课
如何确定点C
问题解决:
1.C为切点。
2.∠OCB=∠OAC
3.=
模型6:“米勒问题”之最大张角
例20.如图,顶点为M的抛物线y=+bx+3与x轴交于A(-1.0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线与另一个点D,作DE ⊥ x轴,垂足为点E.双曲线y=(x>0)经过点D,连接MD,BD.
(1)求抛物线的解析式.
(2)动点P从点0出发,以每秒1个单位长度的速度沿 0C方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
(1)A(-1,0)、C(0,3)、D(2,3)
y +2x+3
模型6:“米勒问题”之最大张角
例20.如图,顶点为M的抛物线y= y=+bx+3与x轴交于A(-1.0),B两点,与y轴交于点C,过点C作CD⊥y铀交抛物线与另一个点D,作DE ⊥ x轴,垂足为点E.双曲线y= (x>0)经过点D,连接MD,BD.
(1)求抛物线的解析式.
(2)动点P从点0出发,以每秒1个单位长度的速度沿 0C方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
思路1:找思路
G
P
模型6:“米勒问题”之最大张角
作△PBD的外接圆⊙G,使⊙G与y轴相切于点P,连接GP,GB,GD,
∵ P(0,t),∴ 设G(r,t),由两点间的距离公式可得:
解得:= =(舍去)
∴∴时, ∠BPD的度数最大。
G
P
例20.如图,顶点为M的抛物线y= y=+bx+3与x轴交于A(-1.0),B两点,与y轴交于点C,过点C作CD⊥y铀交抛物线与另一个点D,作DE ⊥ x轴,垂足为点E.双曲线y= (x>0)经过点D,连接MD,BD.
(2)动点P从点0出发,以每秒1个单位长度的速度沿 0C方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
模型6:“米勒问题”之最大张角
H
思路2:切割线定理
作△PBD的外接圆⊙G与y轴相切于点P,延长BD交y轴于点H,
由B(3,0)、D(2.3)可求得直线BD为:
y=-3x+9
∴H(0,9),HD=2, HB=3,
由切割线定理可得:=60
∴
∴
常见的“隐圆”模型思维导图
中考数学复习--动点中的隐圆问题
在中考数学中,有一些高频考题,如线段的最值问题,动点路程问题,几乎每年各地都会有出现。在这些题目中的图形中往往没有出现“圆”,但在解题时却要用到“圆”的知识点,我们把这样类型的题目称之为“隐圆模型”。
----看不见的圆
如图,在△ABC中,∠ACB=90°,AC=BC=4,点D是BC边的中点,点P是AC边上一个动点,连接PD,以PD为边在PD的下方作等边三角形PDQ,连接CQ.则CQ的最小值是( )
A. B.1 C. D.
如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF,AF交BD于G,现有以下结论:①AP=PF;②DE+BF=EF;③PB﹣PDBF;④S△AEF为定值;⑤S四边形PEFG=S△APG.以上结论正确的有 (填入正确的序号即可).
主从联动
(瓜豆原理)
隐圆
(四点共圆)
图,直尺AB垂直竖立在水平面上,将一个含45°角的直角三角板CDE的斜边DE靠在直尺的一边AB上,使点E与点A重合,DE=12cm.当点D沿DA方向滑动时,点E同时从点A出发沿射线AF方向滑动.当点D滑动到点A时,点C运动的路径长为 _______cm.
在平面直角坐标系中,直线y=﹣x﹣2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a>0)经过A,B两点,并与x轴的正半轴交于点C.
(1)求a,b满足的关系式及c的值;
(2)当a时,若点P是抛物线对称轴上的一个动点,求△ABP周长的最小值;
(3)当a1时,求QD的最大值。
点C在∠BAF的平分线上运动
将
军
饮
马
构
造
二
次
函
数
如图,∠ACB=45°,半径为2的⊙O与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设t=PEPF,则t的取值范围是 .
如图1,已知线段AB,AC,线段AC绕点A在直线AB上方旋转,连接BC,以BC为边在BC上方作Rt△BDC,且∠DBC=30°.
(1)略
(2)略
(3)如图3,若∠BCD=90°,AB=4,AC=2,当AD的值最大时,求此时tan∠CBA的值.
胡
不
归
隐
圆
如图,在△ABC中,AB=5,tan∠C=2,则ACBC的最大值为 .
在平面直角坐标系xOy中,已知抛物线F:y=﹣x2+bx+c经过点A(﹣3,﹣1),与y轴交于点B(0,2).
(1)求抛物线的函数表达式;
(2)在直线AB上方抛物线上有一动点C,连接OC交AB于点D,求的最大值及此时点C的坐标;
胡不归+定角定边
构造二次函数
模型背景
定
角
定
边
定
角
定
边
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足ADCE,则下列结论:①;②∠DFE=135°;③△ABF面积的最大值是44;④CF的最小值是22.其中正确的是( )
A.①③ B.①②④ 、
C.②③④ D.①②③④
如图是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成.在正方形ABCD中,AB=10.下列三个结论:①若tan∠ADF,则EF=2;②若Rt△ABG的面积是正方形EFGH面积的3倍,则点F是AG的三等分点;③将△ABG绕点A逆时针旋转90°得到△ADG',则BG′的最大值为55.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
阿氏圆
定角定高
如图,抛物线y=ax2+bx+c(a<0)的图象交x轴于点A(﹣3,0)、B(1,0),交y轴于点C.以下结论:①a+b+c=0;②a+3b+2c<0;③当以点A、B、C为顶点的三角形是等腰三角形时,c;④当c=3时,在△AOC内有一动点P,若OP=2,则CPAP的最小值为.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
如图,正方形ABCD的边长为1,M、N是边BC、CD上的动点.若∠MAN=45°,则MN的最小值为 .
定点定长
定角定边
如图,在 ABCD中,∠C=120°,AB=8,BC=10,E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,连接AD',BD',则△ABD′面积的最小值为 .
如图,在Rt△ABC中,∠ACB=90°,CA=CB=3,线段CD绕点C在平面内旋转,过点B作AD的垂线,交射线AD于点E.若CD=1,则AE的最大值为 ,最小值为 .
最大张角
如图,已知两条平行线l1、l2,点A是l1上的定点,AB⊥l2于点B,点C、D分别是l1,l2上的动点,且满足AC=BD,连接CD交线段AB于点E,BH⊥CD于点H,则当∠BAH最大时,sin∠BAH的值为 .
模型背景
三、顺应《课程标准》
《课标》课程理念要求:课程目标以学生发展为本,以核心素养为导向,进一步获得数学基础知识、基本技能、基本思想和基本经验(简称“四基”),发展运用数学知识与方法发现、提出、分析和解决问题的能力(简称“四能”),形成正确的情感、态度和价值观。
模型背景
三、顺应《课程标准》
课程目标要求:初中阶段,核心素养主要表现为:抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识,创新意识。
模型背景
三、顺应《课程标准》
课程内容要求:第四学段(7-9年级)掌握(节选)
图形的性质
①掌握基本事实:两点之间线段最短;
②理解垂线段的概念;
③理解圆、弧、弦、圆心角、圆周角的概念。
模型背景
三、顺应《课程标准》
学业质量标准:第四学段(7-9年级)(节选)
知道运动过程的不变量、图形运动的变化特征,能运用几何图形的基本性质进行推理证明。
模型背景
三、顺应《课程标准》
学业水平考试:第四学段(7-9年级)(节选)
适当提高应用性、探究性和综合性试题比例,题目设置要注重创新真实情境,提出有意义的问题,实现核心素养导向的义务教育数学课程学业质量的全面考查。
有“圆” 千里来相会,无“圆” 对面不相识
寻找圆的“影子”, 使得“圆” 形毕露
常见的隐圆模型
模型1:定点定长型
动点P到定点0的距离为d保持不变,则点P的轨迹为以点0为圆心,d为半径的圆弧.
圆的定义:圆是到定点的距离等于定长的点的集合。
o
P
d
模型1:定点定长型
若AB=AC=AD.则点B、C、D在以A为圆心,AB为半径的圆上。
1.几个点到某个定点距离相等可用圆(定点为圆心,相等距离为半径)
模型1:定点定长型
1.几个点到某个定点距离相等可用圆(定点为圆心,相等距离为半径)
例1.如图,已知AB=AC=AD,∠CBD=2 ∠ BDC, ∠ BAC=44°,则∠ CAD的度数为_____.
模型1:定点定长型
例2.在矩形ABCD中,已知AB=2cm,BC=3cm,现有一根长为2cm的木棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为多少?
2.动点到定点距离保持不变的可用圆
方法:先确定定点,定点为圆心,动点到定点的距离为半径。
A
B
D
C
E
F
P
S=2x3-πx
=6-π
A
B
D
C
E
F
P
模型1:定点定长型
2.动点到定点距离保持不变的可用圆
例3.如图,矩形ABCD中,AB=2,AD=3,点E、F分别为AD、DC边上的点,
且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为____
分析:
PA+PG=PA'+PG≥A'G
A'G的最小值为
A'D-DG=5-1=4
A’
一箭穿心
模型1:定点定长型
3.过定点作折叠的可用圆(定点为圆心,对应点到定点的距离为半径)
例4.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是____
【分析】考虑△AMN沿MN所在直线翻折得到△A'MN,可得MA'=MA=1,所以A'轨迹是以M点为圆心,MA为半径的圆弧,连接CM,与圆的交点即为所求的A',此时A'C的值最小,构造直角△MHC,勾股定理求CM,再减去A'M即可.
模型1:定点定长型
3.过定点作折叠的可用圆(定点为圆心,对应点到定点的距离为半径)
例5.如图,在Rt △ABC中, ∠ C=90°,AC=6,BC=8,点F在边AC上,并
且CF=2,点E为边BC上的动点,将△ CEF沿直线EF翻折,点C落在点P处
则点P到边AB距离的最小值是 _____.
【分析】考虑到将△ FCE沿
EF翻折得到△ FPE,可得P点轨迹是以F点为圆心,FC为半径的圆弧:过F点作FH⊥AB,与圆的交点即为所求P点,此时点P到AB的距离最小,由相似或三角函数先求FH,再减去FP,即可得到PH.
一箭穿心+垂线段最短
模型1:定点定长型
例6.如图,矩形ABCD中,AB=4,BC=8,P、Q分别是直线BC、AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△ FEQ,连接PF、PD,则PF+PD的小值是_______.
【分析】F点轨迹是以E点为圆心,EA为半径的圆,作点D关于BC对称点D',连接PD',PF+PD化为PF+PD'.连接ED',与圆的交点为所求F点,与BC交点为所求P点,勾股定理先求ED'再减去EF即可
D'
3.过定点作折叠的可用圆(定点为圆心,对应点到定点的距离为半径)
模型1:定点定长型
4.“瓜豆”里的隐圆(主从联动型,主动点轨迹为圆则从动点的轨迹也是圆)
例7.(泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
解析:
连接AB,取 AB的中点E,连接EM.易得EM 为△ABC的中位线,
EM=BC=1,OE=
OM 的最大值为 EM+OE= + .故选 B
主动点--定点定长型 从动点--定点定长型
E
(瓜豆)微课
A.C.2
模型1:定点定长型
方法二:作点A关于y轴的对称点
例7.(泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.C.2
模型1:定点定长型
4.“瓜豆”里的隐圆(主从联动型,主动点轨迹为圆则从动点的轨迹也是圆)
例8.如图,AB=4,0为AB的中点, ⊙0的半径为1,点P是⊙0上一动点,
以点P为直角顶点的等腰直角△PBC(点P,B,C按逆时针方向排列),则线
段AC长的取值范围是 ____
O '
分析:连接O ‘C,连接OP,易得∠OBP=∠ O B‘C,所以 所以 O ‘C ,所以点C在以O ‘为圆心, 为半径的圆上运动,可求得A O ‘=2 ,因此AC的最大值为+ ,AC的最小值为 ,所以线段AC长的取值范围是 .
模型2:直角对直径
原理:圆O中,圆周角是90°所对的弦是直径。
固定线段AB所对动角∠C恒为90°,则A、B、C三点共圆,AB为直径。
A
B
C(动点)
A
B
C(动点)
模型2:直角对直径
例9.在正方形ABCD中,AD=2,E,F分别为边DC,CB上的点,且始终保持DE=CF,连接AE和DF交于点P,则线段CP的最小值为_____.
【解析】
如图,在△ADE和△ DCF中,AD=DC,
∠ADE=∠DCE,DE=DF
∴ △ ADE△ DCF(SAS)
∴∠DAE=∠CDF
∴∠DAE+∠AED=90°
∴∠CDF+∠AED=90°
∠APD=90 °保持不变
∴点 P的轨迹为以 AD为直径的一段弧上
取 AD 中点 2,连接 C,与该圆弧交点即为点 P,此时 CP值最小,在 Rt△CQD中,CQ=5,CP=CQ-PQ=
模型2:直角对直径
例10.如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF,连接CF交BD于点G,连接BE交AG于点H,若正方形边长为2,则线段DH长度的最小值是____.
【分析】
根据条件可知:∠DAG=∠DCG=∠ABE
易证AG⊥BE,即∠AHB=90°,
所以H点轨迹是以AB为直径的圆弧
当D、H、0共线时,DH取到最小值
勾股定理可求,答案为-1
o
模型2:直角对直径
例11.如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=10,点D是AC上的一
个动点,以CD为直径作圆O,连接BD交圆O于点E,则AE的最小值_____.
【分析】
连接 CE,由于 CD为直径,故∠CED=90°,考虑到 CD 是动线段,故可以将此题看成定线段 CB 对直角∠CEB.取 CB 中点 M,所以E点轨迹是以M为圆心、CB为直径的圆弧,连接AM,与圆弧交点即为所求 E点,此时E值最小,AE=AM-EM=2-2.
模型3:定边对定角
模型解读
定边对定角微课
P(动)
固定线段AB所对动角P为定值则点P运动轨迹为过A、B、C三点的圆
P(动)
原理:弦AB所对同侧圆周角恒相等备注:点P在优弧、劣弧上运动皆可
模型3:定边对定角
例12.如图,等边△ABC边长为2,E、F分别是BC、CA上两个动点,且BE=CF,连接AE、BF,交点为P点,则CP的最小值为________.
【分析】由BE=CF可推得三角形ABE≌三角形BCF,所以∠APF=60°但∠APF所对的边AF是变化的:所以考虑∠APB=120°,其对边AB是定值。所以如图所示,P点轨迹是以点O为圆心的圆弧。(构造OA=OB且∠AOB=120°)当0、P、C共线时,可得CP的最小值,利用Rt△OBC勾股定理求得OC,再减去OP即可.
O
模型3:定边对定角
例13.如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P从点P向半径0A引垂线PH交OA于点H,设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为________.
C
分析:由内心的性质可得∠PIO=135°
连接AI,∵OI平分∠AOP,OP=OA
∴ △AIO△PIO,
∴ ∠AIO=∠PIO=135°
∵ OA为定边,∠AIO=135°为定角
∴ 点P在以OA为弦且圆心角为90°的圆弧上运动
记圆心为点C,易求得
由弧长公式可求得圆心I的运动路径长.
模型3:定边对定角
例14.如图,已知以AB为直径的圆O,C为弧AB的中点,P为弧BC上任意一点,CD垂直CP交AP于D,连接BD,若AB=6.则BD的最小值为_____.
分析:
连接 AC,易得∠P=45°,所以△CDP为等腰直角三角形,
∴∠ADC=135°为定角,AC为定边。
∴圆心角∠AGC=90 °
∵AB=6,∴AC=,∴AG=CG=3
∴BG= =
G
例14.如图,已知以AB为直径的圆O,C为弧AB的中点,P为弧BC上任意一点,CD垂直CP交AP于D,连接BD,若AB=6.则BD的最小值为_____.
“瓜豆”分析--构造“双子型(手拉手模型)”
连接0C,作CG⊥CO,且 CG=C0,连接 0G,OP,易证得COP≌CGD,∴GD=0P=3,为定值。
点D在以G为圆心3为半径的圆弧上。可求得 BG= =
G
方法二:定点定长型
模型4:定角夹定高
【题型背景】
在一些最值问题中,给定一个角,并且过定角的顶点作对边的垂线为定值时,也存在最值问题,面对这种问题我们借助“隐圆”进行说明:我们称这种问题为:“定角夹定高”模型也成“探照灯”模型。
主要解决:(1)线段最短问题:(2)面积最小问题。
[模型]
如右图所示,在△ABC中,∠BAC=为定值,AD为BC边上的高,且AD=h为定值,则底边BC存在最小值,△ABC面积存在最小值, △ABC周长存在最小值。
模型4:定角夹定高
【模型]如右图所示,在三角形ABC中,∠BAC=为定值,AD为BC边上的高且AD=h为定值,则底边BC存在最小值,△ABC面积存在最小值.
[解题突破点]
1.找出“隐圆”——三角形外接圆
2.定高过外心(半径+弦心距>定高),即AB=AC(等腰三角形)
定角定高微课
模型4:定角夹定高
分析:当高经过外心时,BC最小,此时AB=AC,且∠A=60°,所以ABC为等边三角形,所以可得BC=6.
r
例15.如图在△ABC中,∠A=60°,BC边上的高为求BC的最小值。
∵
∴
∴
∴
模型4:定角夹定高
例16.如图,在四边形ABCD中,AB=AD=CD=4,ADBC,∠B=60°,点E、F分别为边BC、CD上的两个动点,且∠EAF=60°,则AEF的面积是否存在最小值 若存在,求出其最小值;若不存在,请说明理由。
F '
O
H
G
分析:如图,将△ADF绕点A顺时针旋转120°到△ABF′,则∠EAF′=60°
易证△AEF≌△AEF′ ,作△AE F′的外接圆⊙O,作OH⊥BC于点H,AG⊥BC于点G,
则∠F′OH=60°,AG,
设⊙O的半径为r,则OH,
∵OA+OH,∴,∴,
∵∠FAE=∠F′AE=∠FOE=60°
∴F′E=
∴S△AEF=S△AEF′EF′ AG,
∴△AEF面积的最小值是4.
模型4:定角夹定高
周长的最小值
某地举办了迎新年大型灯光秀表演.其中一个镭射灯距城墙30米,镭射灯发出的两根彩色光线夹角为60°,如图,若将两根光线(AB,AC)和光线与城墙的两交点的连接的线段(BC)看作一个三角形,记为△ABC,那么该三角形周长有没有最小值?若有,求出最小值,若没有,说明理由.
延长CB至点D,使BD=BA,连接AD,
延长BC至点E,使CE=AC,连接AE。
D
E
当点A、F、G、O四点共线时,半径r最小,r,故DE最小。
解题突破点:AB=AC时,周长最小。
O
F
G
模型4:定角夹定高
定角夹定中线
定角夹定角平分线
中线倍长 定边对定角
作双高 定角夹定高
突破点:AB=AC时,△ABC面积有最大值
突破点:AB=AC时,△ABC面积有最小值
模型5:四点共圆
四点共圆的基本图形
A
B
C
D
C
D
B
A
[对角互补型]
如图,∠A+∠C=180°或∠B+∠D=180°,
则A、B、C、D四点共圆。
[同侧等角型]
如图,∠A=∠C,则A、B、C、D四点共圆。
模型5:四点共圆
例17.如图,在正方形ABCD中,0为AC、BD的交点,△DCE为直角三角形∠CED=90°,∠DCE=30°,若 ,则正方形ABCD的面积为____.
F
分析:过点D作DF⊥OE于点F,设DF=x,则EF=x,OF=
∴
∴
∴
∴
模型5:四点共圆
o
例18.如图,等边△ABC中,AB=6,P为AB边上一动点,PD⊥BC,PE ⊥AC,则DE的最小值为____.
:∵ ∠PEC=∠PDC=90°,
∴ P、D、C、E四点共圆,且CP为直径,O为圆心
∴ ∠EOD=2∠ACB=120°,
∴ DE=要使DE最小,则⊙O的半径r最小,故直径PC最小。
当CP⊥AB时,
∴,,
∴.
模型5:四点共圆
2.手拉手(双子型)中的四点共圆
条件:△0CD∽△0AB
结论:
① △ 0AC ∽ △ 0BD:
②AC与BD交于点E,必有∠AEB=∠AOB;
③点E在△0AB的外接圆上.即O、A、B、E四点共圆. 同理:O、D、C、E也四点共圆.
模型5:四点共圆
2.手拉手(双子型)中的四点共圆
例19.如图①,在钝角△ABC中,∠ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将△ BDE绕点B逆时针方向旋转a度(0大于a小于180);
(1)如图②,当0
如变化,请说明理由;如不变,请求出这个角的度数;
(3)将△BDE从图①位置绕点B逆时针方向旋转180°,求点G的运动路程
模型5:四点共圆
例19.如图①,在钝角ABC中,∠ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将BDE绕点B逆时针方向旋转a度(0a≤180)
(1)如图②,当0
如变化,请说明理由;如不变,请求出这个角的度数;
(3)将ΔBDE从图①位置绕点B逆时针方向旋转180°,求点G的运动路程.
H
K
的长
点G的运动路程是的长的两倍.
米勒(Johannes Miier 1436--1476)德国数学家,对三角做出了巨大贡献,是欧洲最有影响的数学家之一。米勒发表的《三角全书》,是使得三角学在欧洲取得独立地位的第一部系统性著作。
1471年,米勒提出了一个有趣的问题:在地球表面什么部位,一根垂直的悬杆呈现最长 即在什么部位,视角最大 最大视角问题是数学史上100个著名的极值问题之一。
模型6:“米勒问题”之最大张角
米勒问题一般的描述是:
已知,点A、B是∠MON的OM边上的两个定点,C是ON边上的一个动点,当C在何处时,∠ACB最大
问题解决:
当且仅当△ABC的外接圆与边ON
相切于点C时,角ACB最大。
模型6:“米勒问题”之最大张角
最大张角微课
如何确定点C
问题解决:
1.C为切点。
2.∠OCB=∠OAC
3.=
模型6:“米勒问题”之最大张角
例20.如图,顶点为M的抛物线y=+bx+3与x轴交于A(-1.0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线与另一个点D,作DE ⊥ x轴,垂足为点E.双曲线y=(x>0)经过点D,连接MD,BD.
(1)求抛物线的解析式.
(2)动点P从点0出发,以每秒1个单位长度的速度沿 0C方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
(1)A(-1,0)、C(0,3)、D(2,3)
y +2x+3
模型6:“米勒问题”之最大张角
例20.如图,顶点为M的抛物线y= y=+bx+3与x轴交于A(-1.0),B两点,与y轴交于点C,过点C作CD⊥y铀交抛物线与另一个点D,作DE ⊥ x轴,垂足为点E.双曲线y= (x>0)经过点D,连接MD,BD.
(1)求抛物线的解析式.
(2)动点P从点0出发,以每秒1个单位长度的速度沿 0C方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
思路1:找思路
G
P
模型6:“米勒问题”之最大张角
作△PBD的外接圆⊙G,使⊙G与y轴相切于点P,连接GP,GB,GD,
∵ P(0,t),∴ 设G(r,t),由两点间的距离公式可得:
解得:= =(舍去)
∴∴时, ∠BPD的度数最大。
G
P
例20.如图,顶点为M的抛物线y= y=+bx+3与x轴交于A(-1.0),B两点,与y轴交于点C,过点C作CD⊥y铀交抛物线与另一个点D,作DE ⊥ x轴,垂足为点E.双曲线y= (x>0)经过点D,连接MD,BD.
(2)动点P从点0出发,以每秒1个单位长度的速度沿 0C方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大 (请直接写出结果)
模型6:“米勒问题”之最大张角
H
思路2:切割线定理
作△PBD的外接圆⊙G与y轴相切于点P,延长BD交y轴于点H,
由B(3,0)、D(2.3)可求得直线BD为:
y=-3x+9
∴H(0,9),HD=2, HB=3,
由切割线定理可得:=60
∴
∴
常见的“隐圆”模型思维导图
同课章节目录
