八年级数学上册期末调研试卷一(适合徐州地区含答案)
文档属性
| 名称 | 八年级数学上册期末调研试卷一(适合徐州地区含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 20:11:31 | ||
图片预览



文档简介
2024~2025学年度第一学期期末学情调研卷一
八年级数学试题
一、迭择题(本大题有8小题,每小题3分,共24分)
1.近几年我国新能源汽车市场爆发式增长,成为全球最大的新能源汽车市场.下列新能源车标图案中轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4 个
2.估计的值是在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
3.下列长度的三条线段,不能组成直角三角形的是( )
A. 0.3, 0.4, 0.5 B.2,3.4 C. 6, 8, 10 D. 9, 12, 15
4.在平面直角坐标系中,点P(-2,-1)关于x轴的对称点坐标是( )
A. (-2, 1) B. (2, 1) C. (2, -1) D. (-2, -1)
5.一次函数y=-2x-4的图像不经过第( )象限.
A.一 B.二 C.三 D.四
6.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.ZA=∠D B. AB=DC C. ∠ACB=∠DBC D. AC=BD
7.一次函数y=kx+b(k≠0)中,x与y的部分对应值如下表:
x -2 -1 0 1 2
y -8 -6 -4 -2 0
那么一元一次方理kx+b=0的解为( )
A. x= - 4 B. x= -2 C. x =0 D. x=2
8.如图,在Rt△ABC中,∠BAC=90°,∠C=56°,AD是斜边BC上的中线,将△ABD沿AD翻折,使点B落在点F处,线段AF与BC相交于点E,则∠AED的度数为( )
A.100 B. 80° C.78° D.39°
二、填空题(本大题有8小题,每小题4分,共32分)
9.计算:25的平方根是______
10.在平面直角坐标中,点P(3,-2)在第_____________象限.
11.若一次函数y=kx+2的图像经过点(-3,5),则k的值为______
12.如图,在3×3的正方形网格中,点M,N在格点上,若P点也在格点上,且△PMN是等腰三角形,则符合条件的点P的个数为_______.
13.如图,在△ABC中,AC=6cm,P是AB的中点,PQ⊥AB交AC于点Q,△BCQ的周长是10cm,则BC的长为_______..
14.如图,在△ABC中,AB=AC,BC=5,BD⊥AC于点D,且BD=4,则AC的长为_______.
15.点P(a,b)在函数y=5x+1的图像上,则代数式5a-b+2的值等于______
16.在平面直角坐标系中,已知点A(1,6),B(4,-2),点M在x轴上,当AM_BM最大时,点M 的坐标为_______.
三、解答题(本大题有9小题,共84分)
17.(本题10分)
(1)计算
(2)求x的值:5x =20
18.(本题8分)已知:如图,∠BAD=∠ABC,AD=BC
求证:AC=BD.
19.(本题8分)如图,已知AB=CD AF=DE BE=CF
求让:(1)△ABF≌△DCE:
(2) OE=OF
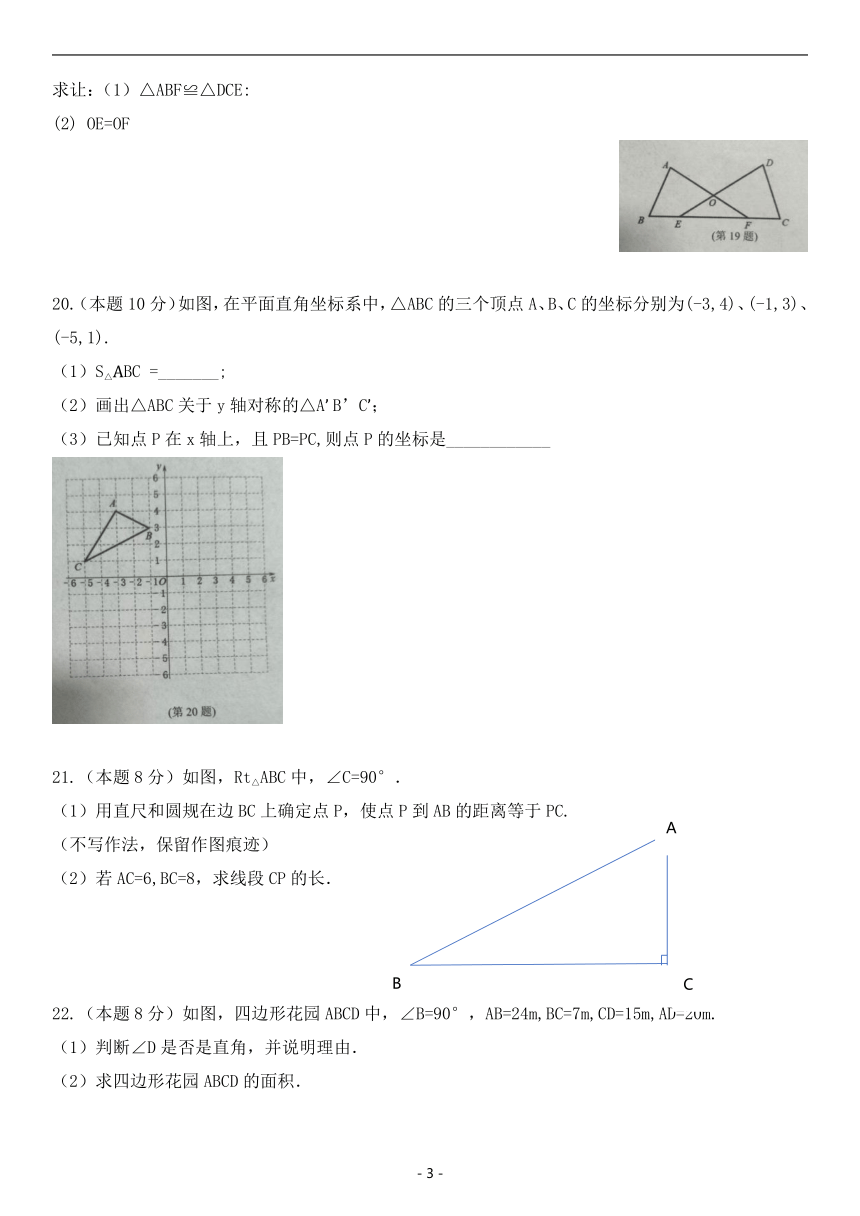
20.(本题10分)如图,在平面直角坐标系中,△ABC的三个顶点A、B、C的坐标分别为(-3,4)、(-1,3)、(-5,1).
(1)S△ABC =_______;
(2)画出△ABC关于y轴对称的△A’ B’C’;
(3)已知点P在x轴上,且PB=PC,则点P的坐标是____________
21.(本题8分)如图,Rt△ABC中,∠C=90°.
(1)用直尺和圆规在边BC上确定点P,使点P到AB的距离等于PC.
(不写作法,保留作图痕迹)
(2)若AC=6,BC=8,求线段CP的长.
22.(本题8分)如图,四边形花园ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形花园ABCD的面积.
23.(本题8分)某产品每件成本12元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x/元 … 15 20 25 …
y/件 … 25 20 15 …
已知日销售量y是销售价x的一次函数.
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为36元时,此时每日的销售利润是多少元
24.(本题12分)请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图像:
①列表填空:
x … -3 -2 -1 0 1 2 3 …
y … …
②描点、连线,画出y=|x|的图像:
(2)结合所画图象,写出y=|x|两条不同类型的性质;
(3)写出函数y=|x|与y=|x+2图像的平移关系.
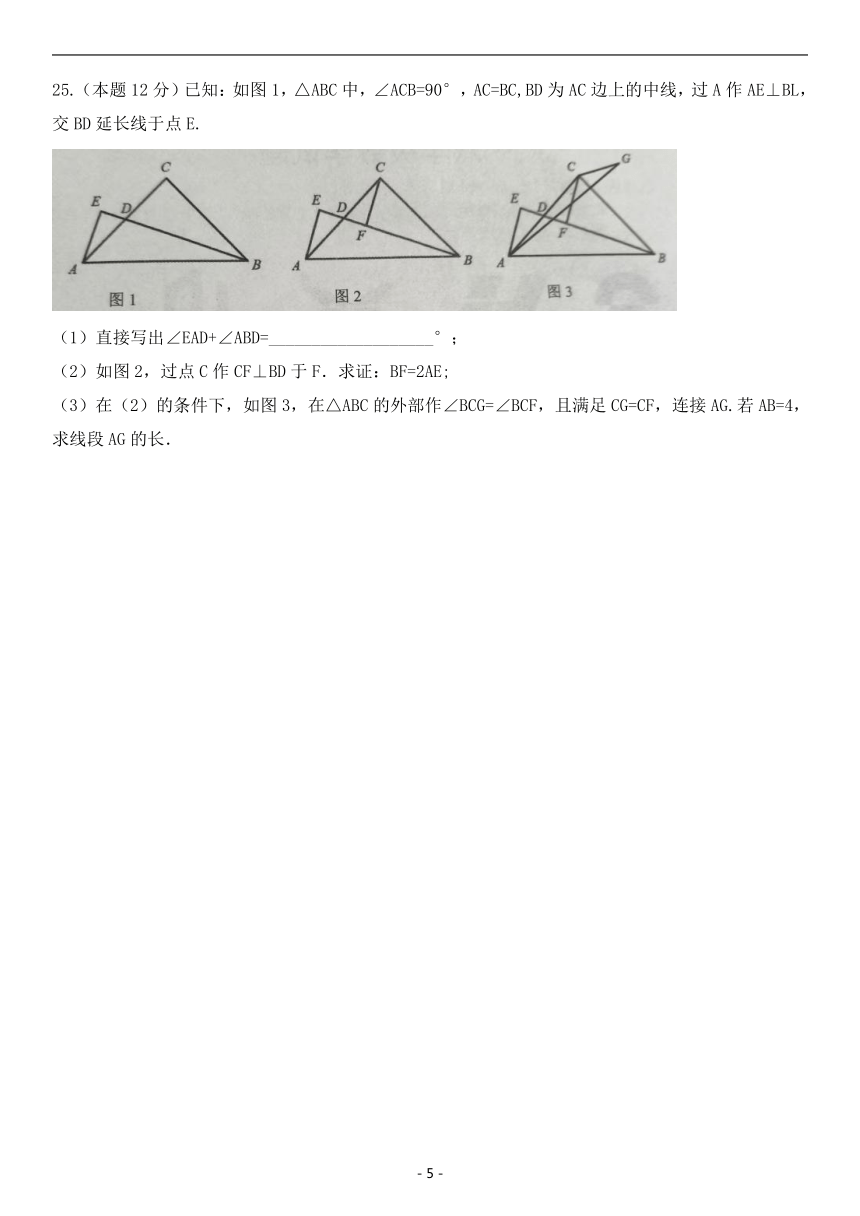
25.(本题12分)已知:如图1,△ABC中,∠ACB=90°,AC=BC,BD为AC边上的中线,过A作AE⊥BL,交BD延长线于点E.
(1)直接写出∠EAD+∠ABD=___________________°;
(2)如图2,过点C作CF⊥BD于F.求证:BF=2AE;
(3)在(2)的条件下,如图3,在△ABC的外部作∠BCG=∠BCF,且满足CG=CF,连接AG.若AB=4,求线段AG的长.
- 1 -
- 10 -
八年级数学试题
一、迭择题(本大题有8小题,每小题3分,共24分)
1.近几年我国新能源汽车市场爆发式增长,成为全球最大的新能源汽车市场.下列新能源车标图案中轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4 个
2.估计的值是在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
3.下列长度的三条线段,不能组成直角三角形的是( )
A. 0.3, 0.4, 0.5 B.2,3.4 C. 6, 8, 10 D. 9, 12, 15
4.在平面直角坐标系中,点P(-2,-1)关于x轴的对称点坐标是( )
A. (-2, 1) B. (2, 1) C. (2, -1) D. (-2, -1)
5.一次函数y=-2x-4的图像不经过第( )象限.
A.一 B.二 C.三 D.四
6.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.ZA=∠D B. AB=DC C. ∠ACB=∠DBC D. AC=BD
7.一次函数y=kx+b(k≠0)中,x与y的部分对应值如下表:
x -2 -1 0 1 2
y -8 -6 -4 -2 0
那么一元一次方理kx+b=0的解为( )
A. x= - 4 B. x= -2 C. x =0 D. x=2
8.如图,在Rt△ABC中,∠BAC=90°,∠C=56°,AD是斜边BC上的中线,将△ABD沿AD翻折,使点B落在点F处,线段AF与BC相交于点E,则∠AED的度数为( )
A.100 B. 80° C.78° D.39°
二、填空题(本大题有8小题,每小题4分,共32分)
9.计算:25的平方根是______
10.在平面直角坐标中,点P(3,-2)在第_____________象限.
11.若一次函数y=kx+2的图像经过点(-3,5),则k的值为______
12.如图,在3×3的正方形网格中,点M,N在格点上,若P点也在格点上,且△PMN是等腰三角形,则符合条件的点P的个数为_______.
13.如图,在△ABC中,AC=6cm,P是AB的中点,PQ⊥AB交AC于点Q,△BCQ的周长是10cm,则BC的长为_______..
14.如图,在△ABC中,AB=AC,BC=5,BD⊥AC于点D,且BD=4,则AC的长为_______.
15.点P(a,b)在函数y=5x+1的图像上,则代数式5a-b+2的值等于______
16.在平面直角坐标系中,已知点A(1,6),B(4,-2),点M在x轴上,当AM_BM最大时,点M 的坐标为_______.
三、解答题(本大题有9小题,共84分)
17.(本题10分)
(1)计算
(2)求x的值:5x =20
18.(本题8分)已知:如图,∠BAD=∠ABC,AD=BC
求证:AC=BD.
19.(本题8分)如图,已知AB=CD AF=DE BE=CF
求让:(1)△ABF≌△DCE:
(2) OE=OF
20.(本题10分)如图,在平面直角坐标系中,△ABC的三个顶点A、B、C的坐标分别为(-3,4)、(-1,3)、(-5,1).
(1)S△ABC =_______;
(2)画出△ABC关于y轴对称的△A’ B’C’;
(3)已知点P在x轴上,且PB=PC,则点P的坐标是____________
21.(本题8分)如图,Rt△ABC中,∠C=90°.
(1)用直尺和圆规在边BC上确定点P,使点P到AB的距离等于PC.
(不写作法,保留作图痕迹)
(2)若AC=6,BC=8,求线段CP的长.
22.(本题8分)如图,四边形花园ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形花园ABCD的面积.
23.(本题8分)某产品每件成本12元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x/元 … 15 20 25 …
y/件 … 25 20 15 …
已知日销售量y是销售价x的一次函数.
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为36元时,此时每日的销售利润是多少元
24.(本题12分)请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图像:
①列表填空:
x … -3 -2 -1 0 1 2 3 …
y … …
②描点、连线,画出y=|x|的图像:
(2)结合所画图象,写出y=|x|两条不同类型的性质;
(3)写出函数y=|x|与y=|x+2图像的平移关系.
25.(本题12分)已知:如图1,△ABC中,∠ACB=90°,AC=BC,BD为AC边上的中线,过A作AE⊥BL,交BD延长线于点E.
(1)直接写出∠EAD+∠ABD=___________________°;
(2)如图2,过点C作CF⊥BD于F.求证:BF=2AE;
(3)在(2)的条件下,如图3,在△ABC的外部作∠BCG=∠BCF,且满足CG=CF,连接AG.若AB=4,求线段AG的长.
- 1 -
- 10 -
同课章节目录
